前、后加载低压涡轮高升力叶型流动损失机理大涡模拟研究

赵 磊，刘兆方，罗华玲

（中国航发商用航空发动机有限责任公司，上海200241）

在民用航空发动机中，高升力叶型设计是低压涡轮气动设计技术的重要发展方向之一。通常，叶型负荷用Zweifel升力系数（Zw）来表征，Zweifel升力系数大于1.0的叶型设计被称为所谓的高升力叶型设计，而升力系数大于1.2的设计被称为超高升力叶型设计（Ultra-high lift）[1]。在相同的速度三角形条件下，叶型升力的提高可以通过减小叶片轴向弦长或者减少叶片数来实现，从而可以减轻低压涡轮的重量。但是，随着叶型负荷的提高，必然导致叶型吸力面扩散区逆压梯度的增强，传统的定常设计思想认为，这会导致低压涡轮叶型损失在高空低雷诺数条件下急剧恶化，定常来流条件的叶栅试验也证实了这一结论（如图1所示），因此上世纪90年代前低压涡轮的叶型升力水平都在1.0以下。

图1 传统叶型设计思想叶型吸力面流动示意图

实际低压涡轮叶片是工作在非定环境中的，剑桥大学怀特实验室Hodson教授领导的研究组针对低压涡轮内部环境下的尾迹诱导转捩相关问题开展了大量的研究工作[1-7]。研究表明，尾迹诱导转捩所形成湍流区与寂静区（Calmed region）边界层速度剖面因较之层流速度剖面更饱满而更能抵抗分离，从而可以削弱分离甚至完全抑制分离，减小分离流动损失。这就意味着，虽然在定常流动、低湍流度假设条件下高负荷设计叶型因存在边界层分离导致其损失高于低升力设计叶型，但在上游尾迹扫掠的非定常流动条件下，因边界层分离得到抑制且尾迹诱导转捩导致的湍流边界层损失相对较小，高升力设计叶型的损失有可能低于低升力叶型的损失。比如，图2给出了两种不同升力设计叶型（Datum与Blade H，前者升力系数为0.87，后者升力系数为1.05）的表面等熵速度分布（定常流动条件）及对应的叶型损失对比，可以看出在非定常流动条件下（存在上游尾迹扫掠），高升力设计的Blade H叶型损失低于低升力设计的Datum叶型损失。

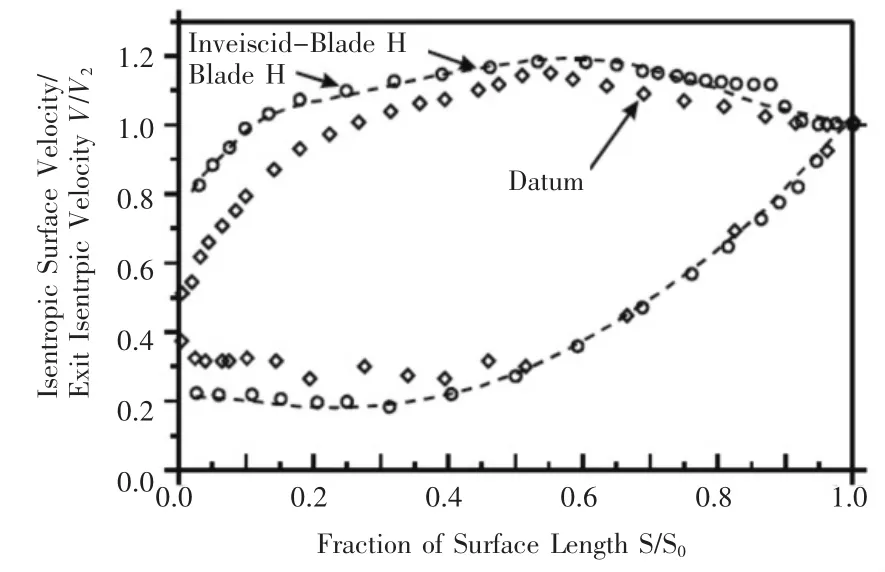
图2 两种不同升力设计叶型表面速度分布及损失对比[8]

随着对低压涡轮内部非定常流动环境下叶片边界层分离及转捩问题的理解认识不断加深，研究者们发现在尾迹的扫掠下高负荷叶型的叶型损失并不会显著的提升，高升力叶型设计的思想和方法得以逐步确立，并在工程设计中获得应用。随后，罗罗公司BR-710/715、TRENT系列发动机[9]，发动机联盟的GP7000系列等发动机，GE公司GE90与GEnx等系列发动机低压涡轮都开始采取高升力叶型设计。

国内，北航[10，11]、西工大[12]，商发[13，14]等机构的研究学者同样在相关领域开展了大量的数值和试验研究，推动了国内相关技术水平的发展，研究结果指出分离点动量厚度雷诺数是影响高升力叶型损失的重要因素，但是对如何设计叶型的峰值马赫数位置并无明确结论。本文通过对相同升力系数具有相同分离点动量厚度雷诺数的前、后加载叶型进行大涡模拟分析，研究其流场和损失特性，为高升力叶型设计中峰值马赫数位置的选取提供指导。

1 研究方法

1.1 研究对象

以某型低压涡轮导叶的中截面叶型的雷诺数（Re=1.2×105，定义见公式1）及进出口气流角为输入，设计了Zweifel升力系数为1.2的两套叶栅，设计叶型参数如表1所示，其中叶栅1和叶栅2具有相同的分离点动量厚度雷诺数，但叶栅1为后加载叶型，叶栅2为加载叶型，如图3所示。通过两套叶栅的对比，可以分析出加载位置对高升力叶型性能的影响。

式中，u2为叶栅出口截面的特征速度，即平均速度；ρ为空气密度；b为叶栅弦长；μ为空气粘性系数。

表1 叶型主要设计参数

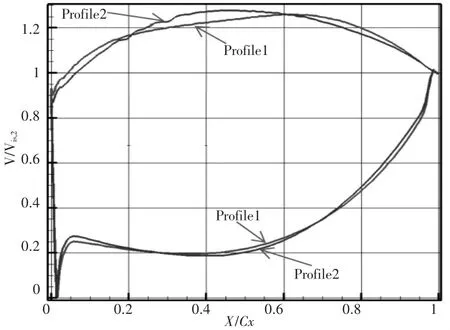
图3 高升力叶型压力分布对比

1.2 数值方法

利用尾迹扫掠的非定常效应来抑制分离是高升力叶型设计的关键，而对转捩位置与长度的模拟直接影响叶栅性能，目前采用湍流模型的URANS方法还缺乏准确捕捉这一现象的能力，因而大涡模拟（LES）精度较高，被广泛用于此类问题的数值研究。本文采用了二维大涡模拟方法，在不同尾迹通过频率和雷诺数条件下对上述2套叶栅进行了模拟分析，上游尾迹的扫掠效应通过上游周期性运动的圆棒来模拟。

计算网格由ANSYSICEM进行划分，为二维结构化网格。圆棒区域节点数为5.7万，网格分布如图4（a）所示，圆棒栅距与叶栅相同，直径为4 mm，叶型轴向弦长为100 mm，圆棒中心与叶栅前缘距离为0.5倍叶栅轴向弦长。叶栅域节点数为23.6万，网格分布如图 4（b）所示。总节点数为 29.3万。壁面 Δy+均小于1，近壁区网格层间延伸比为1.1，网格流向尺寸Δs+均小于2.5.为降低出口边界反射对上游流场计算的影响，将出口延伸至6倍轴向弦长。

图4 计算域网格分布

大涡模拟计算采用的是商用计算流体动力学软件Fluent，亚格子尺度模型选用Smagorinsky-Lilly模型，动态应力修正模型与Cs取0.1的修正模型计算结果接近，为保证数值计算的稳定性，选择了Cs为0.1的模型修正方法。对于上游带棒的算例，圆棒域设为运动计算域，网格移动速度根据各算例工况的尾迹通过频率决定。空间离散选用有界中心差分格式，时间离散选用有界二阶隐式格式。非定常时间步设置为圆棒通过周期的1%.

本文分别对两套叶栅在四种雷诺数工况（Re=0.8 × 105、1.2 × 105、1.5 × 105和 1.8 × 105） 和三种来流条件（Fr=0.0、0.3和0.6）进行了计算，其中尾迹折合频率Fr的定义为：

式中，ubar为模拟尾迹的圆棒线速度，tbar为模拟尾迹的圆棒节距，通过调节算例中圆棒的运动速度来改变尾迹通过频率。当Fr=0时，表示栅前无圆棒，即定常来流条件。

2 结果与分析

2.1 雷诺数效应

图5给出了叶栅1在定常来流条件（Fr=0.0）不同雷诺数下叶栅尾缘的时均速度云图。图中低速区即为边界层区域，可以看到，吸力面边界层从叶身中部（峰值马赫数位置之后）开始显著增大，然后逐步发展为分离。尾缘时均边界层厚度随雷诺数变化明显，雷诺数越小，时均边界层厚度最大，表明分离泡随着雷诺数增大而变小，符合气动动力学一般规律。

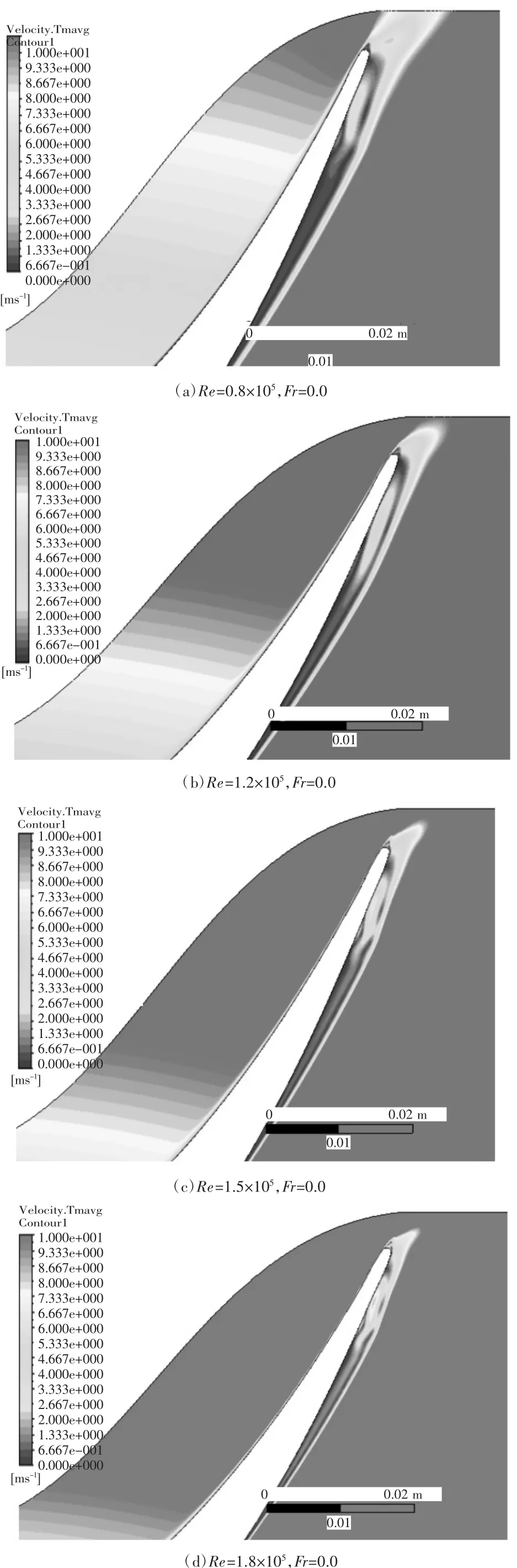
图5 叶栅1时均速度分布云图

图6给出了叶栅1在定常来流条件（Fr=0.0）不同雷诺数下吸力面时均边界层动量厚度和动量厚度雷诺数沿轴向的变化趋势。其中，纵坐标分别为边界层动量厚度和动量厚度雷诺数，横坐标是轴向相对弦长，AC表示轴向弦长。可以看到，叶栅1在四个雷诺数工况下，分离起始点的位置都比较接近（在77%～79%之间），随着雷诺数的增大，分离点位置略微向后推移，表明雷诺数的变化对叶型吸力面分离起始位置的影响比较小，分离点动量厚度雷诺数的增大主要是由于主流速度的增大导致的。

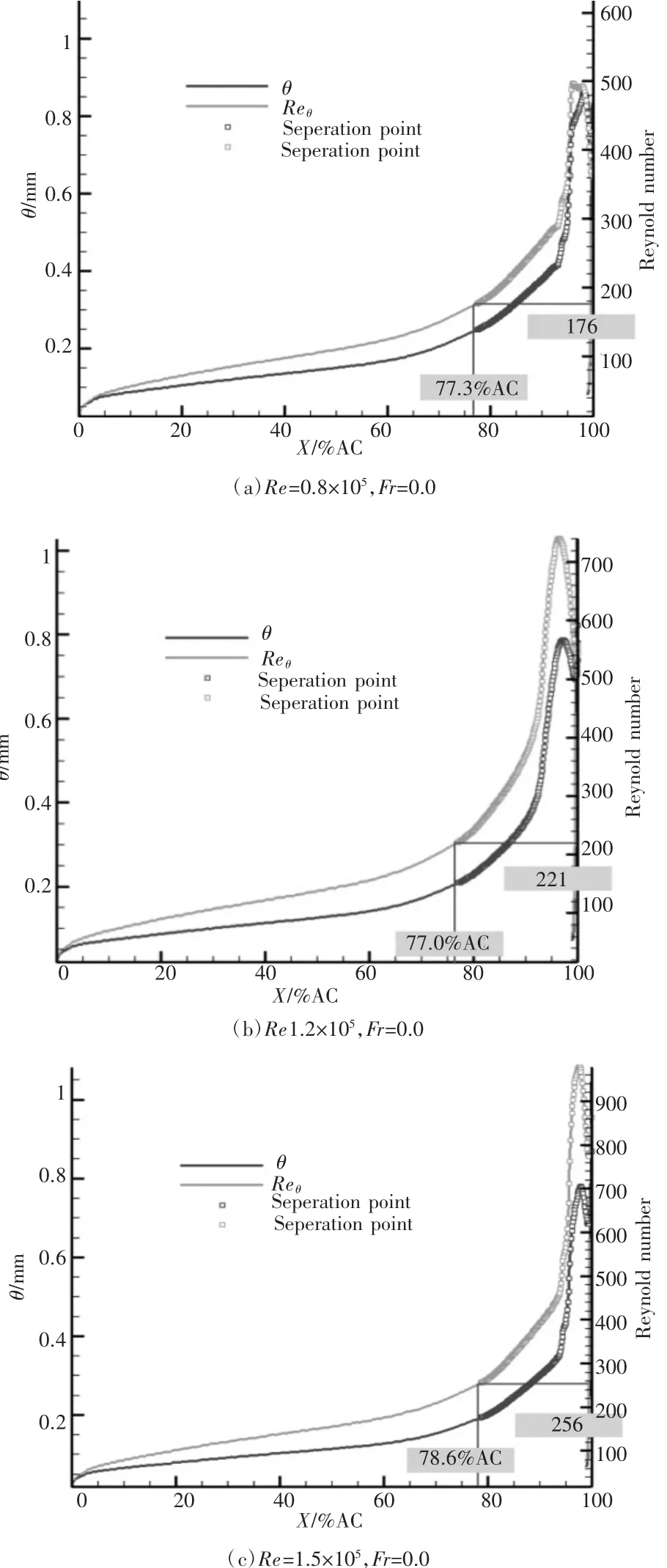
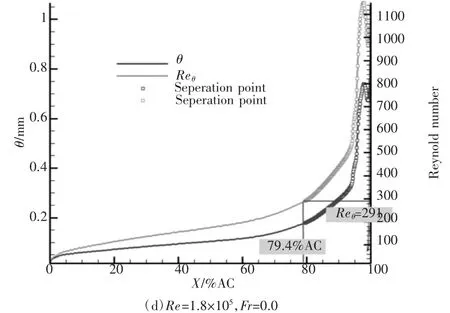
图6 叶栅1时均动量厚度和动量厚度雷诺数的沿程变化

2.2 尾迹效应

图7 给出了叶栅1不同尾迹通过频率下叶栅尾缘部分区域的时均速度云图。从图中可以看到，上游无尾迹时，时均边界层厚度以及分离区相对较大。在尾迹折合频率为0.3时，时均边界层厚度和分离区长度均减小，说明上游尾迹可以有效地抑制叶片吸力面分离。在尾迹折合频率增大到0.6时，吸力面边界层的时均分离泡基本得到了抑制。

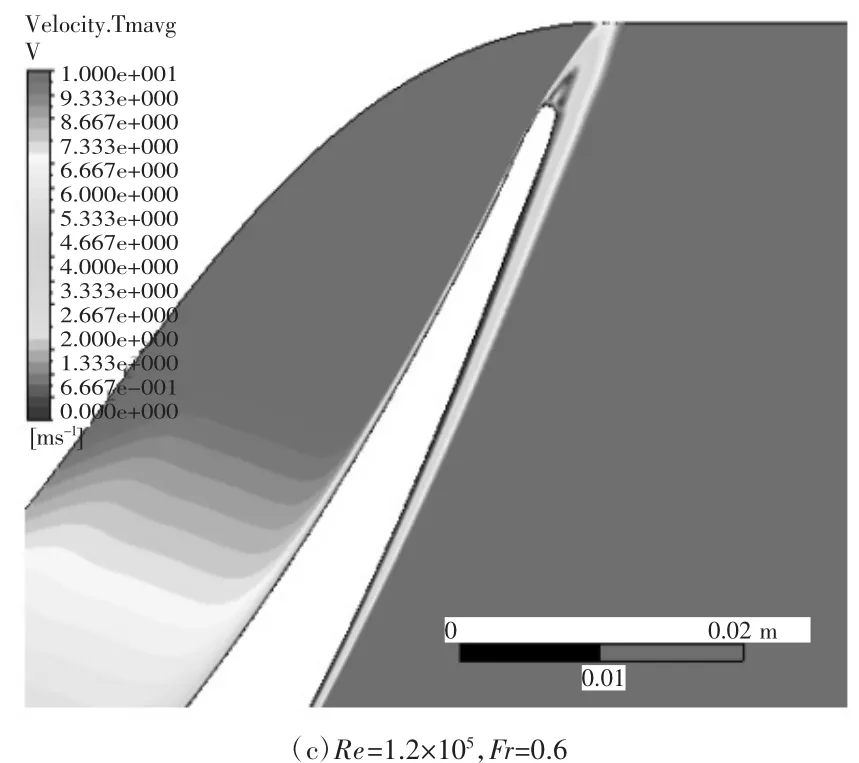
图7 叶栅1不同尾迹通过频率下时均速度分布云图

图8 给出了叶栅1不同尾迹通过频率下吸力面边界层动量厚度和动量厚度雷诺数的沿程变化。从结果中可以看到，尾迹通过频率为0.3时，时均分离点从无尾迹下的77.0%AC（轴向弦长）后移到了83.1%AC，而尾迹通过频率增大到0.6时，吸力面分离点到了接近尾缘的位置（94.2%AC），且分离区大大减小，与图7现象一致。

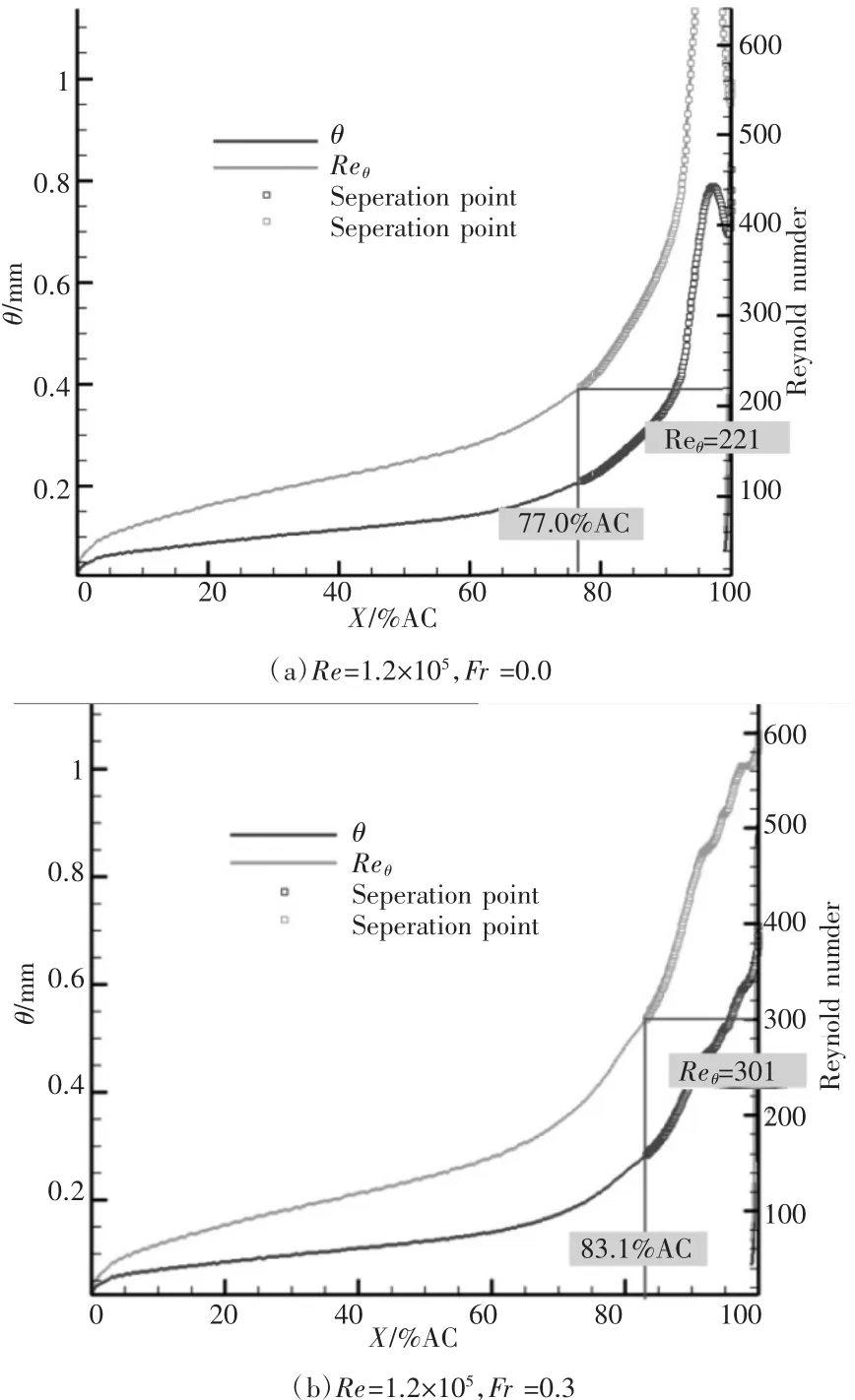
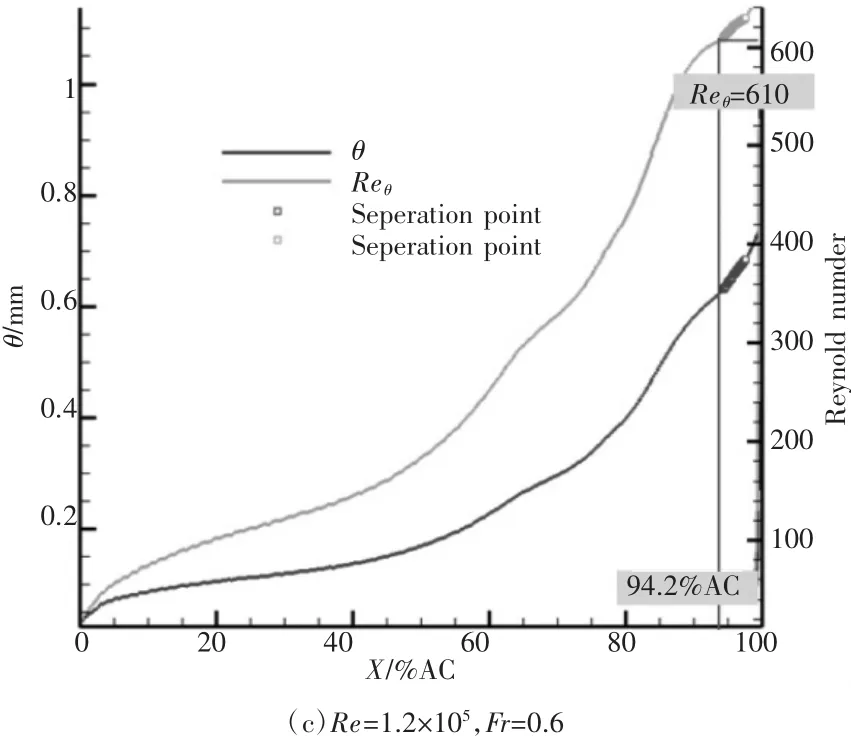
图8 叶栅1不同尾迹通过频率下时均动量厚度和动量厚度雷诺数的沿程变化

图9 给出了叶栅1不同尾迹通过频率下损失系数的比较，得益于尾迹对分离泡的抑制作用，可以看到叶型损失随着尾迹通过频率的增大而减小。

图9 叶栅1损失系数比较

通过时空图可以更直观的揭示尾迹对边界层的影响机制，分析边界层参数的非定常变化规律。图10给出了叶栅1不同尾迹通过频率吸力面边界层位移厚度的时空演化图，S/S0表示吸力面相对弧长，t/t0表示相对时刻，白色实线表示分离起始点。从图10中可见，上游尾迹的存在使吸力面边界层分离点向后移动，尾迹折合频率为0.6时，部分时刻下，吸力面分离现象消失，且整体分离区域变小，分离时间较短。此外，随着尾迹折合频率的增大，由于上游尾迹抑制了吸力面边界层分离，吸力面靠近尾缘区域的边界层位移厚度也逐渐减小。

图10 叶栅1不同尾迹通过频率吸力面边界层位移厚度时空图

图11 给出了叶栅1不同尾迹通过频率吸力面剪切应力的时空演化图。可以看到，在上游无尾迹时，吸力面边界层中是层流分离（0.65S/S0处开始）和自然转捩（0.87S/S0至尾缘）。在上游尾迹折合频率为0.3时，在0.8～0.9相对时刻范围内，尾迹开始诱导分离区边界层的流体发生转捩，使该区域壁面剪切应力增大，随着尾迹向下游迁移，其扰动减弱，转捩过程被削弱。同时，尾迹诱导转捩后，分离在湍流边界层下得到抑制，分离区推后（如白线所示），自然转捩区也推后（0.91S/S0至尾缘）。图 11（c）Fr=0.6的结果可见，尾迹诱导转捩的起始位置相比于Fr=0.3时有所提前，在0.5S/S0位置处开始，表明较高的尾迹折合频率导致在层流分离点之前即诱发转捩。

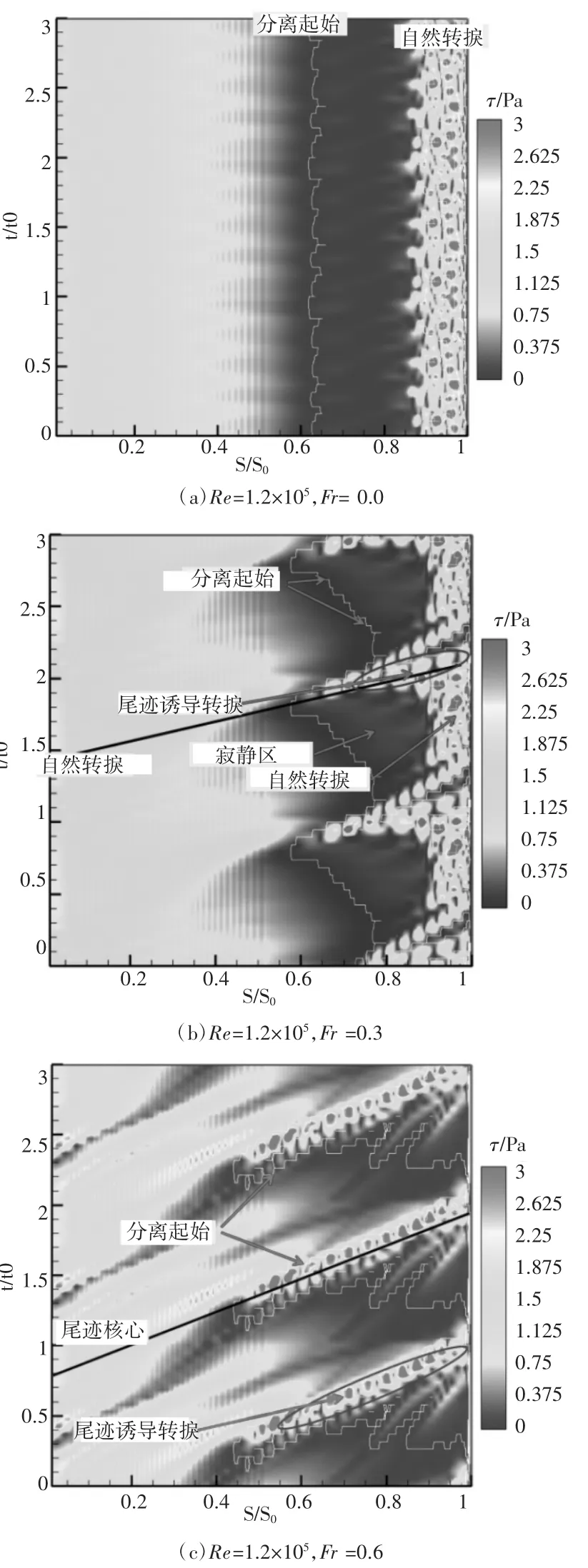
图11 叶栅1不同尾迹通过频率吸力面剪切应力时空图

同时，还可以看到，随着尾迹折合频率的增大，扰动的强度和频率均增大，使分离区进一步向后推甚至消失，转捩区也更快地向湍流变化，形成再附。在下游，尾迹离开后，即使再次发生分离，回流区和转捩区的范围也很小。图11从非定常变化的角度揭示了随着尾迹折合频率增大，叶栅1叶型损失逐渐降低背后的物理过程。

上述结果表明，尾迹对高升力叶型的吸力面流动特征有很大的影响，尾迹会诱导边界层转捩，进而起到对边界层分离泡的抑制作用，引起叶栅性能的显著变化。

2.3 前后加载叶型对比

图12给出了无尾迹情况下叶栅2的计算结果，对比相同状态下叶栅 1的结果（图 8（a）和图 10（a）），叶栅2的时均分离起始位置在60%吸力面弧长位置（73.3%轴向弦长），相比叶栅1提前，其自然转捩带来的湍流边界层范围也较叶栅2小一些，但是因为在这一雷诺数工况下两者均为开式分离，所以其叶型损失系数相差不大，分别为0.054 5（叶栅1）和0.054 3（叶栅2），与两套叶栅尾缘动量厚度的对比一致。此外，两套叶栅设计的分离点动量厚度雷诺数相同。

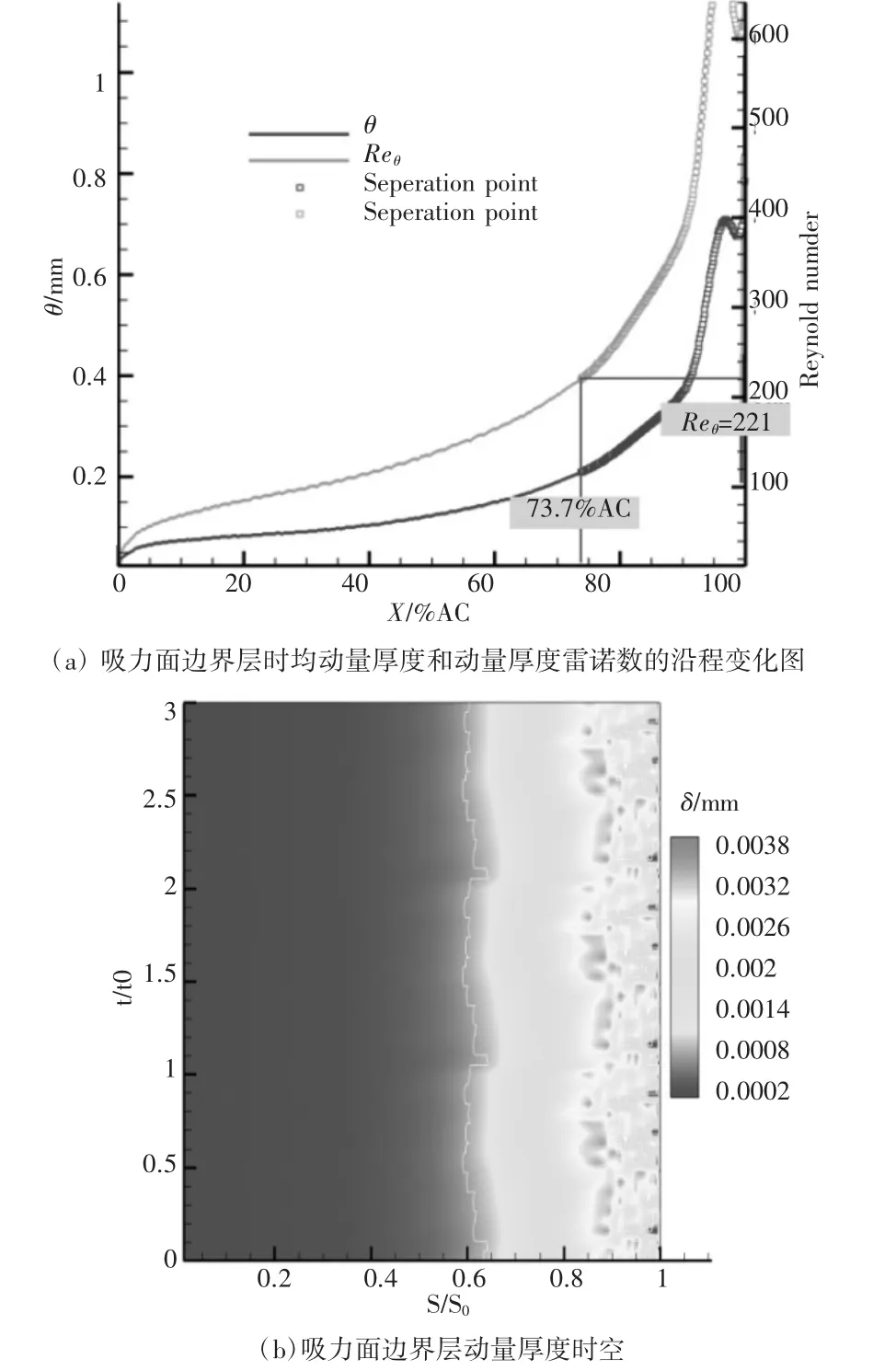
图12 叶栅2 Re=1.2×105，Fr=0.0

此外，计算结果表明，设计点雷诺数下（Re=1.2×105）叶栅1和叶栅2的分离点动量厚度雷诺数相同，均为221，相比定常RANS计算偏小。

图13给出了叶栅2在设计点雷诺数Fr=0.3尾迹通过频率下边界层参数的沿程变化及时空图。对比叶栅 1 的结果（图 8（b）、图 10（b）和图 11（b）），两套叶栅尾迹诱导转捩的位置均发生在层流分离起始点附近，而叶栅1的位置更加靠后。叶栅1时均分离为开式状态，而叶栅2为闭合分离泡，因此尽管叶栅1的湍流边界层损失更小，但由于分离损失在叶栅1中任然占主导，所以叶栅2（0.044 4）的损失较叶栅1（0.049 5）仍然更小。

图13 叶栅2 Re=1.2×105，Fr=0.3

图14给出了叶栅2设计点雷诺数Fr=0.6尾迹通过频率下边界层参数的沿程变化及时空图。对比叶栅 1 的结果（图 8（c）、图 10（c）和图 11（c）），由于尾迹增强，此时两套叶栅的时均分离泡均为闭合状态，其分离损失量级相当，但是后加载的叶栅1湍流浸湿面积更小，所以其损失也更小（叶栅1=0.040 5，叶栅2=0.054 7）。

图14 叶栅 2 Re=1.2×105，Fr=0.6

以上结果表明，当尾迹增大到足以使时均分离泡闭合时，适当的后加载可以减小湍流浸湿面积，提升叶栅性能。

3 结束语

本文针对性地设计了前、后加载的两套高升力叶型，通过二维大涡模拟计算，分析了两套叶栅在定常和非定常来流条件下吸力面边界层的演化规律和损失特性，结果表明，在尾迹扫掠使时均分离泡闭合时，相比前加载叶型，后加载的高升力叶型可以减小叶栅的湍流浸湿面积，提高叶栅性能。