气动折入装置异向射流场中纱线的运动规律

刘宜胜， 裘燚斌， 吴震宇

(浙江理工大学 机械与自动控制学院， 浙江 杭州 310018)

从20世纪单向引纬[1]被提出开始，无梭织机逐步取代了有梭织机，迅速占据世界织机的主要市场，但单向引纬时每根纬纱必须剪断，不能像有梭织机一样织出光滑的布边[2]。毛边折入装置是无梭织机解决布边问题的装置之一，近几年来纯气动毛边折入装置因其高效节能等因素得到了较好的推广。

为对纯气动毛边折入装置进行不断优化，郭岭岭等[3-4]对该装置进行了大量的实验研究，得出了斜吹、折入孔空气压力的范围以及一些影响折入效果的工艺参数。杨鑫忠等[5]设计了一种通过电磁阀控制压缩气流开闭的纯气动折入装置，能准确地将12～15 mm长度的纬纱纱头折入织口内达到光边效果。他们通过不断地实践对纯气动毛边折入装置进行了一定的优化，但没有对纱线在该装置气流场中的运动进行流固耦合分析。

流固耦合的数值求解方法在持续发展中，也是目前研究领域最热门的方向之一，而纱线作为一种柔性体在流体中运动的流固耦合问题涉及到了多个学科，有较大的研究难度[6]。针对稳定流动的黏性流体作用在弹性物体表面上这个现象，GALDI G等[7]通过纳维斯托克斯方程控制流体运动，并分析了该现象的流固耦合理论。DONEA J等[8]通过Lagrange-euler有限元方法来建立瞬态动力学模型，在瞬态动力学增加载荷的过程中该模型可推测流体和固体之间的非线性响应，该算法提出了一种更简捷、更精确的方法来分析耦合作用，震荡和旋转的流场是被允许的，不会使网格在计算过程中产生畸变。PEI Zeguang等[9]以有限单元法为基础，建立了一种柔性且具有弹性的纤维模型，通过建立纤维和气流的流固耦合模型，在喷气涡流纺喷嘴的二维流场中对纤维的实时运动进行仿真模拟。

本文选用计算流体动力学(CFD)软件ADINA建立二维纱线结构模型以及折入装置气流场模型进行固体与气流流固耦合仿真模拟。通过分析纱线在该气流场中的运动规律，对纱线在该气流场中的折入机制进行研究，以期为进一步优化纯气动毛边折入装置提供理论参考。

1 纱线和折入装置气流场控制方程

1.1 纱线控制方程

在折入过程中，忽略纱线表面的粗糙度和运动过程中纱线截面的变化，将其简化成一个各向同性的线弹性体[10]。在拉格朗日坐标系下的控制方程表示为

(1)

式中：ρf为纱线密度；u为纱线每个单元的位移；t为时间；s为关于拉格朗日坐标的向量微分算子；σij为应力张量；s为Lagrange坐标矢量；g为当地的重力加速度。

当折入过程中纱线轴向受到的载荷不超出它的弹性范围，在纱线和气流的流固耦合过程中，可将纱线视为线弹性体。在二维仿真模型中，纱线的线弹性体本构模型可表示为

(2)

(3)

(4)

(5)

式中：σxx、σyy为轴向主应力；εxx、εyy分别为对应的主应变；τxy为切应力；γxy为切向应变；a、b为弹性系数；G为剪切模量；E为弹性模量；υ为泊松比。

纱线密度ρf可用测量得到的线密度ρl和直径D通过下式计算得到：

(6)

本文对纱线在水平平面流场中的运动规律进行研究，这里忽略重力对纱线的影响，但需要考虑纱线模型的密度，设定纱线的控制参数如下：1)纱线密度为500 kg/m3；2)纱线的弹性模量为80 MPa；3)纱线的泊松比为0.3。在ADINA前处理中，设定纱线模型的网格类型为二维实体模型，并进行网格划分。纱线边界与流场边界会触碰且互相作用，纱线的边界设定成流固耦合边界。

1.2 折入装置气流场的控制方程

该折入装置通过空压机将空气压缩后喷射，因此该折入装置流场属于气流场。将斜吹、折入气流看作一种可压缩的非定常理想气体，对于该气流的纳维斯托克斯方程为

(7)

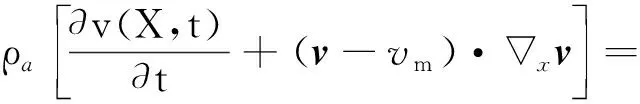
(8)

式中：p为气体压强；v为气流速度矢量；vm为流体网格的移动速度；x为基于欧拉坐标的nabla算子；ρa为气流密度，相对应的ρa0为当p=0时气体的初始密度；T为柯西应力张量，其定义为

T=-pI+μ[xv+]

(9)

式中：I为单位张量；μ为气体黏度。

本文利用基本的K-ε湍流模型对折入气流场进行仿真模拟。在该模型中，空气的黏度μa表示为

μa=μ0+μt

(10)

(11)

式中：μ0为层流黏度；μt为湍流黏度；K和ε分别为湍动能和湍流耗散率，并且被定义为

(12)

(13)

式中v′为平均脉动速度。

K和ε则由以下2个辅助传递方程决定：

(14)

(15)

其中对应参数由以下公式确定：

(16)

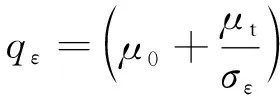
(17)

SK=2μtD2-ρε+B

(18)

(19)

(20)

(21)

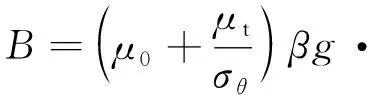
(22)

式中，K-ε湍流模型的常数有cμ、σK、c1、c2、c3、σε和σθ，对应参数设置如表1所示。

表1 K-ε模型的参数设定Tab.1 Parameter values in K-ε model

在ADINA前处理中，将气流场设定为一种可压缩的理想气体，将该气流场设定为K-ε模型，并设置K-ε模型的参数赋予整个流场。设定流场模型的网格类型为二维流场的薄板模型，并进行网格划分。

2 流固耦合方法及边界条件设定

2.1 流固耦合求解方法

流固耦合常用的求解方法主要有单向耦合和双向耦合；而在气流与纱线的流固耦合模拟中，纱线产生较大的形变，会对纱线周围的气流特征产生一定影响，因此，无法忽略纱线对气流的影响，需要采用双向耦合的数值计算方法。

在ADINA软件中，双向耦合有迭代耦合与直接耦合2种。直接耦合在计算时需要占用很大的内存，但计算速度比迭代耦合法更快，因此本文使用直接耦合方法。 在直接耦合解法中，结构方程和流体方程都在一个方程中，该方程可表示为

(23)

且Xk+1=Xk+ΔXk

(24)

(25)

(26)

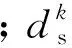
直接耦合法的计算过程包括以下几个步骤：1)设定初始解X0=Xt以及初始边界条件；2)整合流体和固体的结构方程，得到纱线与气流耦合的方程组；3)求解方程组，并计算应力和位移残量，与设定的容差值进行比较。若解没有收敛，并没有达到最大迭代次数，返回步骤2)开始下一次迭代，否则程序中断，输出不收敛信息。然后保存并输出纱线结构与气流体的计算结果。

2.2 流固耦合边界条件

为对折入气流场与纱线进行流体与固体耦合数值仿真，需要在ADINA STRUCTURES模块中建立纱线的柔性体固体结构模型和在ADINA CFD中建立折入气流场的结构模型，共同导入到ADINA软件的FSI求解器中进行模拟计算。纱线模型的边界与流场模型的边界紧密连接，因此，纱线与气流体之间的接触发生在2个模型的边界上，即流固耦合界面。而仿真中的流固耦合边界需要满足位移协调和力平衡条件：

ds=df

(27)

n·τa=n·τf

(28)

式中：ds为固体的位移；df为流体的位移；τa与τf分别为固体和流体的应力；n为边界上的法向量。

满足上述条件，可将流体与固体的边界紧密贴合，使耦合顺利进行。在其边界上，可将流体的分布力看作作用在结构节点上的集中力。它的积分形式可表示为

(29)

式中，hd为固体模型结构的位移。

3 折入装置气流场的几何模型

纯气动毛边折入装置气流场的几何模型如图1所示，其中A处粗线条显示为斜吹孔，B处粗线条显示为折入孔，下方整个矩形区域为斜吹和折入混合气流场计算域。首先气流从斜吹孔进入，从斜吹气流出口射出，并进入外部的大气环境中作用于纱线，将纱线吹弯，关闭斜吹气流，打开折入气流，使纱线进入折入状态。斜吹和握持气流的入口设定条件为压力入口，气流孔的孔壁看作无摩擦的壁面，而流场区域边界设定条件为压力出口，将与纱线表面接触的边缘设定为流固耦合边界。目前纯气动毛边折入装置对于10 mm长的纱线有很好的折入效果，可与仿真形成鲜明的对比，因此，在二维仿真中，设置纱线线头的长度为10 mm，初始状态下为水平不弯曲的线。

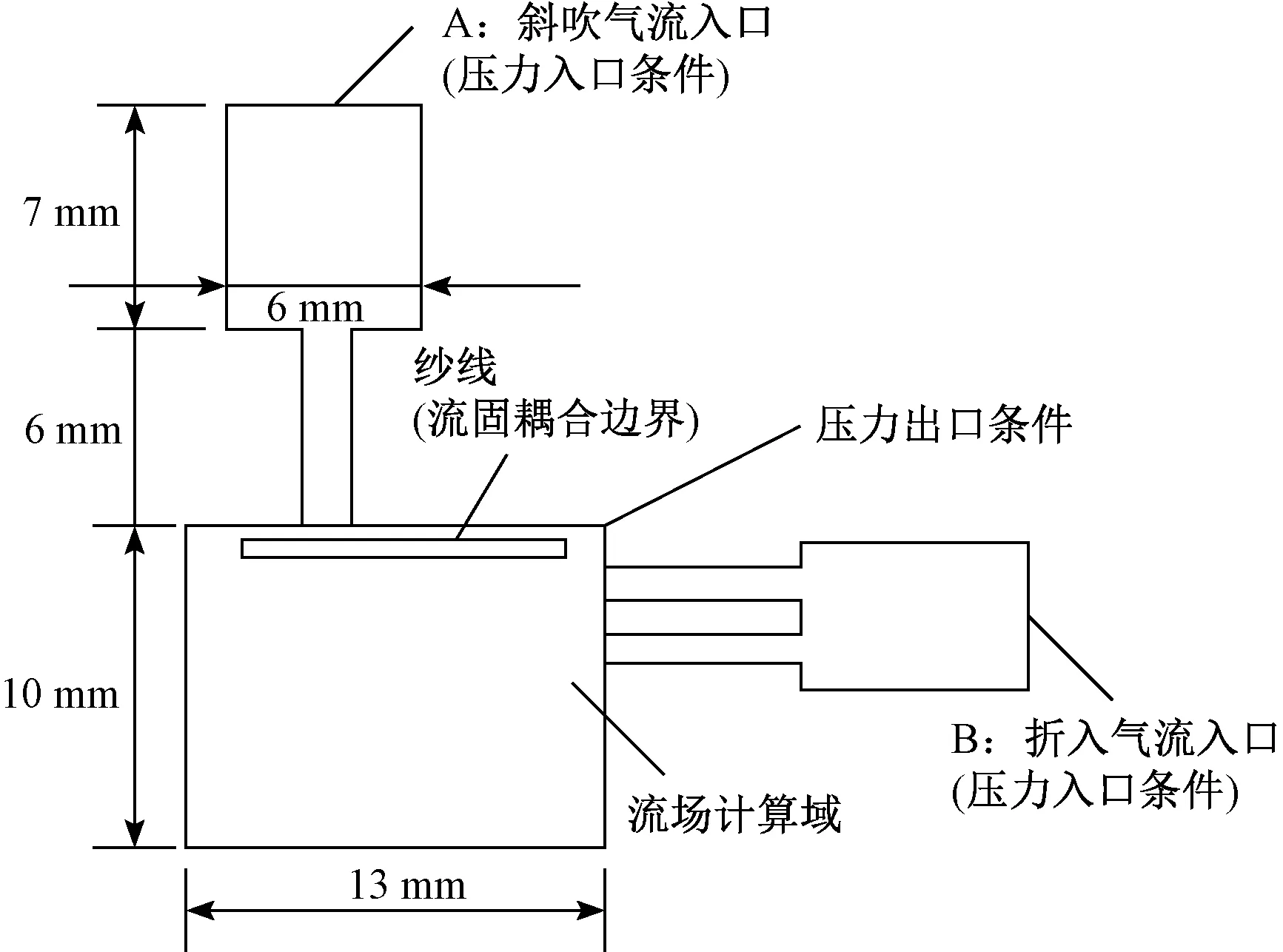
图1 折入装置气流场的几何模型Fig.1 Geometric model of folding device airflow field

由于纱线折入装置气流场中运动时会产生较大的位移并弯曲产生形变，改变流场边界，由Euler方式描述得到的流场网格容易失真。为了保证顺利进行流固耦合模拟，可采用ADINA软件中的一种网格自适应技术。

4 仿真结果与分析

4.1 在斜吹气流作用下纱线的运动规律

在二维模拟中，从射流孔射出的气流的流速可分为切向速度和轴向速度2种分量。切向速度和喷嘴轴线垂直，是横向的；而轴向速度和喷嘴轴线重合，是纵向的[11]。切向速度与轴向速度互相垂直。在斜吹气流的轴向速度分量的喷射下，纱线逐渐向-y方向弯曲，逐渐向外扩展。

在实际工作中，纯气动毛边折入装置中斜吹孔压力为0.25 MPa，折入孔的压力为0.35 MPa。为方便进行数值模拟，仿真中将2个入口压力统一设置为0.3 MPa。斜吹孔的入口以0.3 MPa的压缩空气入射，在孔内加速后，射入纱线周边气流场中。图2示出纱线在斜吹气流作用下不同时间段运动轨迹以及流场压力速度云图。

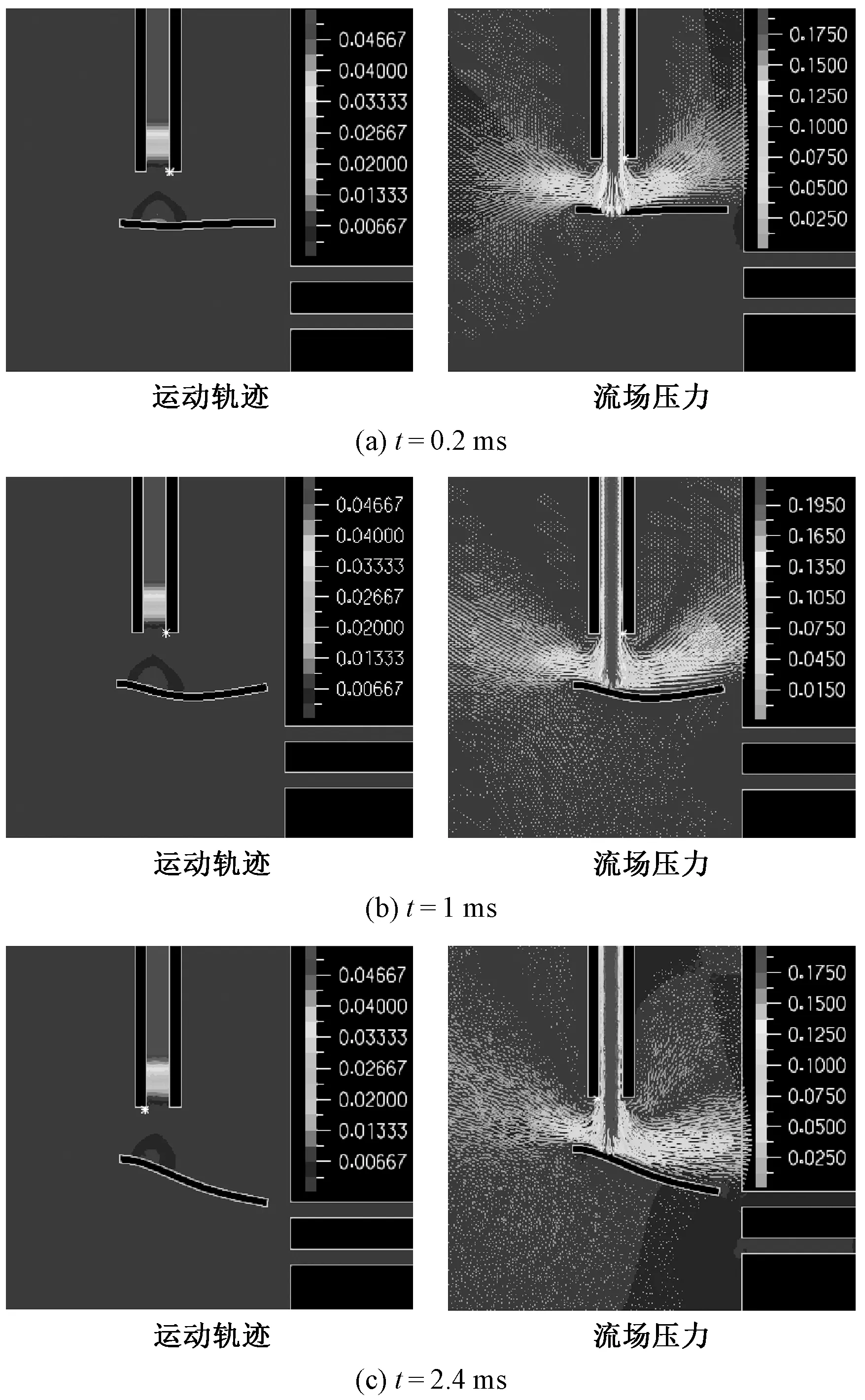
注：压力单位为MPa；速度单位为m/s。下同。图2 10 mm长的纱线线头在斜吹气流作用下不同时间段运动轨迹及流场压力速度云图Fig.2 Motion curves of yarn with length of 10 mm at different time intervals with contours of pressure and velocity under oblique airflow effect

从图2(a)可看出，在斜吹气流射入纱线周围空气中，纱线阻碍气流的运动，使气流减速并发生流向改变，导致无法及时扩散，在纱线内侧积聚，形成高压区，使纱线开始向-y方向弯曲，并逐渐扩散。随着纱线被斜吹气流推动，逐渐弯曲，弯曲程度逐渐扩大。图2(b)示出纱线在弯曲程度扩大的同时，也在开始向下运动。气流逐渐对纱线右端也开始产生作用，对比图2(a)和(b)可看出，纱线在弯曲程度扩大的同时，其上侧内部的高压区最高静压力也在扩大。从图2(c)可看出，随着斜吹气流的持续作用，纱线已经逐步呈现向下运动趋势，对比图2(b)可看出，高压区的最高静压也有逐步减弱，说明纱线在逐步向下运动且逐渐趋于平缓时，对气流的阻碍作用有所减弱，气流也有明显的减速。

4.2 在折入气流作用下纱线的运动规律

折入孔的入口同样以0.3 MPa的压缩空气入射，在孔内加速后射入纱线周边气流场中。图3示出纱线在斜吹气流作用下不同时间段运动轨迹以及流场压力速度云图。

图3 10 mm长的纱线线头在折入气流作用下不同时间段运动轨迹及流场压力速度云图Fig.3 Motion curves of yarn with length of 10 mm at different time intervals with contours of pressure and velocity under folding airflow effect

当纱线在斜吹气流作用下，向下运动倾斜到一定程度时，关闭斜吹气流，开启折入气流，在折入气流作用一段时间后，从图3(a)、(b)中可看出纱线头端阻碍了气流运动，只是气流迅速向外扩散，在纱线头端部位形成高压区，推动纱线向-x方向弯曲。在折入气流作用一段时间后，纱线头端高压区逐渐变大，并有向纱线其他部位发展的趋势。在气流高压区的挤压作用下，纱线逐步向-x方向移动，已经被吹弯，有折入的趋势。由图3(c)看出，在5.7 ms时，纱线线头已经完成折入，高压区已经有纱线头端移向末端。

综上可看出，高压区的移动，有助于折入气流持续推动纱线进入折入状态。在纱线进入到最终的折入状态时，折入部分的纱线会发生轻微抖动现象，不影响折入效果。

4.3 不同长度的线头折入效果对比分析

纱线在斜吹-折入气流场中的运动规律会因为周围气流场的分布特征改变而改变，也会因为纱线的性能、工艺参数等因素受到影响。纱线线头的长度是影响折入效果的主要因素之一，本文采用长度分别为10、12、15 mm且直径为0.5 mm的线头，研究这3种不同长度的纱线在同一斜吹-折入气流场中的运动规律。图4、5分别示出12 mm长的纱线线头在斜吹和折入气流场的作用下不同时间段的运动轨迹，最终在5.7 ms完成折入。

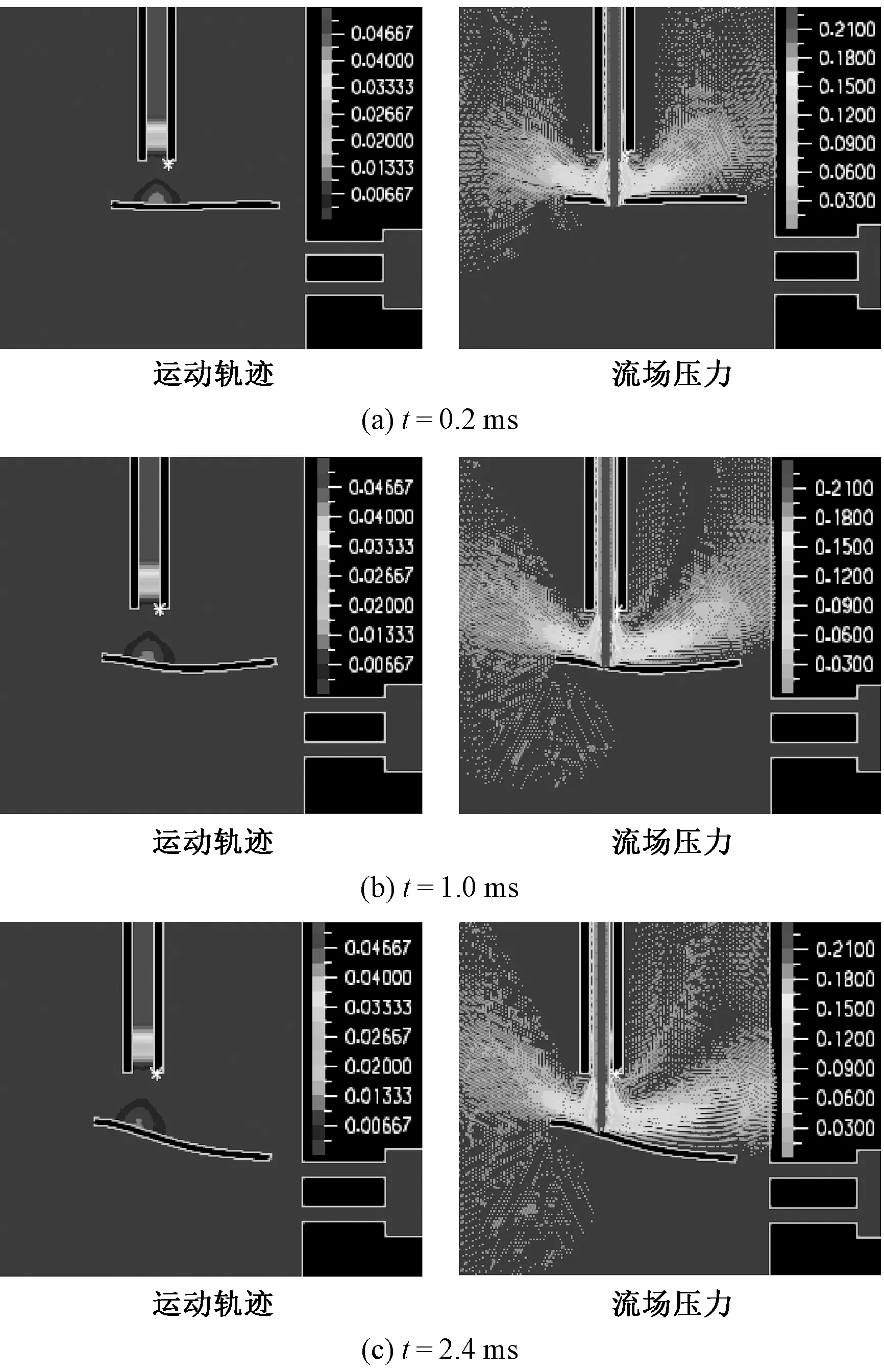
图4 12 mm长的纱线线头在斜吹气流作用下不同时间段运动轨迹及流场压力速度云图Fig.4 Motion curves of yarn with length of 12 mm at different time intervals with contours of pressure and velocity under oblique airflow effect

图5 12 mm长的纱线线头在折入气流作用下不同时间段运动轨迹及流场压力速度云图Fig.5 Motion curves of yarn with length of 12 mm at different time intervals with contours of pressure and velocity under folding airflow effect

图6、7分别示出15 mm长的纱线线头在斜吹-折入气流场作用下在不同时间段的运动轨迹，最终在7.4 ms时完成折入。

对比10、12、15 mm长的纱线线头的仿真结果可发现，纱线线头在斜吹和折入气流作用下的运动轨迹基本相同，且随着纱线线头长度的增加，在斜吹气流作用于纱线头端的时间也在增加，导致15 mm长的线头折入比10 mm长的线头慢。而在折入气流作用下，纱线线头越长，向-x方向移动的速率也越快，说明线头长度的减小也会加大折入的难度。

5 实验结果与分析

通过纯气动毛边折入装置对10、12、15 mm长度的纱线线头进行折入实验，并用摄像机进行拍摄。实验中，纯气动折入装置的斜吹气流入口压力为0.25 MPa，折入气流入口压力为0.35 MPa。图8分别示出折入过程。与图2～7对比可以发现，3种不同长度的纱线线头的最终折入效果与实验结果基本吻合。

织机主轴转1圈，梭口经过开放、静止以及闭合3个阶段，它们的时间长短分别以开放角、静止角以及闭合角表示，而能够用于纯气动折入装置工作的时间大约为满开到投梭的时间，如图9所示。

通过测量得到投梭与满开之间的角度α为27.36°，整个折入过程经历时间t为5.7 ms，织机转速的计算公式可表示为

(30)

通过计算可以得出，该装置可用于转速为800 r/min的无梭织机光边处理。

图6 15 mm长的纱线线头在斜吹气流作用下不同时间段运动轨迹及流场压力速度云图Fig.6 Motion curves of yarn with length of 15 mm at different time intervals with contours of pressure and velocity under oblique airflow effect

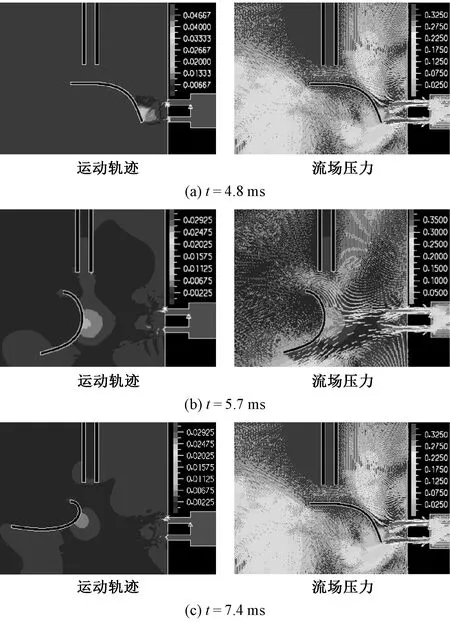
图7 15 mm长的纱线线头在折入气流作用下不同时间段运动轨迹及流场压力速度云图Fig.7 Motion curves of yarn with length of 15 mm at different time intervals with contours of pressure and velocity under folding airflow effect

图8 不同长度的线头折入过程Fig.8 Folding process of yarn with different lengths

图9 综框运动时间分配图Fig.9 Motion time distribution diagram of heald frame

6 结 论

通过ADINA软件对纱线斜吹、折入气流场进行了二维流固耦合仿真，结果表明：在空间异向射流作用下，斜吹和折入气流使用0.3 MPa的入口压力，可使10 mm长的纱线完成折入过程；当斜吹气流开始射入纱线周围空气中，纱线阻碍了气流的运动，使气流减速，导致无法及时扩散，在纱线内侧积聚，形成高压区，驱使纱线开始向-y方向弯曲，斜吹气流作用时间为2.6 ms；当纱线弯曲到一定程度时，折入气流作用在纱线头端，以相同的原理趋势纱线向-x方向弯曲，在5.7 ms时完成折入状态。

FZXB