Phase Sensitive Photonic Flash∗

Xin-Yun Cui(崔馨匀),Zhi-Hai Wang(王治海), and Jin-Hui Wu(吴金辉)

Center for Quantum Sciences and School of Physics,Northeast Normal University,Changchun 130024,China

AbstractWe theoretically propose a photonic flash based on a linearly coupled cavity system.Via driving the two side cavities by external fields,it forms a cyclic energy-level diagram and therefore the phase difference between the driving fields acts as a controller of the steady state due to the quantum interference effect.In the optical trimer structure,we show that the perfect photonic flash can be realized in the situation of resonant driving.The perfect photonic flash scheme is furthermore generalized to multiple coupled cavity system,where the cavities with odd and even number turn bright and dark alternatively.Our proposal may be applied for designing the quantum neon and realizing a controllable photonic localization.

Key words:phase control,photonic flash,coupled cavity system

1 Introduction

Coherent photonic control anddesigning photonic devices are of potential application in quantum information processing,and the coupled cavity array system provides an ideal platform for achieving such tasks.

In the coupled cavity array system,which can be realized by the photonic crystal,[1]toroid micocavity[2]as well as superconductive transmission line,[3−4]the coherent photonic control has invoked a lot of attentions.In the ideal situation,where the decay of the cavities is neglected,kinds of single-photon devices have been theoretically proposed within the scattering frame,such as quantum transistor,[5]quantum router[6]and quantum frequency converter.[7−9]On the other hand,in the coupled cavity array with loss,it has been shown that the non-equilibrium quantum phase transition,which is related to the steady state,may occur in some nonlinear systems when the driving and dissipation are both present.[10−15]Therefore,it supplies a photonic platform to simulate many-body phenomenon in condensed matter physics.[16−17]Naturally,the steady state in the coupled cavity array with only linear interaction deserves more exploration.

In this paper,by investigating the photonic distribution of steady state in a linearly coupled cavity array system,we propose a scheme to realize photonic flash.We here use the phrase “photonic flash” to refer that when some of cavities in the coupled cavity array are completely dark,the other ones are completely bright,and the bright and dark cavities can be exchanged by tuning the system parameters appropriately.In our scheme,the two side cavities are driven by a pair of external fields,we will show that the phase difference between the driving fields acts as an ideal controller for the steady state,which stems from the quantum interference effect among the multiple transition channels.As a simple example,we sketch the realization of dark cavity in an optical trimer,and show that we can construct a perfect photonic flash under the situations(i)the central cavity of the trimer is lossless and(ii)the two side cavities are driven resonantly.Generalizing the scheme to an array of multiple coupled cavities,we show that the cavities with odd and even number will be bright and dark alternatively by adjusting the phase difference.Therefore,we design a scalable photonic flash based on linearly coupled cavity array system.Instead of controlling each cavity individually,we here only drive the two side cavities,regardless of the total number of the cavities,to overcome the difficulties of addressing.As the potential application in the designing of photonic device and quantum simulation based on our proposal,we also give a simple remark on realizing of quantum neon and controllable photonic localization.

The rest of the paper is organized as follows.In Sec.2,we present the model of an optical trimer and the steady state values.We discuss in Sec.3 the condition to realize perfect photonic flash in the trimer structure and generalize it to multi-coupled-cavity system in Sec.4.At last,we discuss the effect of quantum noise and give a brief remark and conclusion in Sec.5.

2 Model of Optical Trimer

The optical trimer system under consideration is sketched in Fig.1,in which the cavities 1,3 are coupled to the cavity 2 simultaneously and are driven by classical if elds with the same frequency ωd.In the rotating frame with respect to the frequency of the driving fields,the Hamiltonian can be written as(here and after

where∆i= ωi− ωd(i=1,2,3)is the detuning between the i-th cavity and the driving fields.Here,ωiis the resonant frequency of cavity i,which is described by the annihilation operator ai.J is nearest inter-cavity coupling strength. λ1and λ3are the driving strengths to cavity 1 and 3,respectively.φ is the phase difference between the two driving fields,which will play an important role in the controlling of photons.Without loss of generality,we assume that all the parameters are real.

Fig.1 The scheme of an optical trimer for photonic flash,where the two side cavities are driven by classical fields.

Assuming the decay rate of the i-th cavity is γi(>0),the dynamics of the system is determined by the Heisenberg-Langevin equation(neglecting the fluctuations)

Then,the steady-state values of the system are immediately given by

3 Photonic Flash in the Trimer

As discussed above,the phase difference is a potential controller for the photonic state in an optical trimer,which supplies us a convenient way to design the coherent optical device,such as photonic flash,utilizing the interference effect.Here,we use the phrase“photonic flash”to mean that,by adjusting only the phase difference between the driving fields,we will make part of the cavities reaches their vacuum steady state,while the intensities in other cavities reach their maximum values.In other words,we will realize the bright and dark cavities simultaneously,and they can be controllably swapped.

To be explicit,we consider a simple scheme in which∆1= ∆2= ∆3= ∆,λ1= λ2= λ3= λ,γ1= γ3= γ,γ2= γ′.According to the formula in Eqs.(6),the condition for ⟨a1⟩=0 is

and the condition for ⟨a3⟩=0 is

Obviously,Eq.(7)or Eq.(8)implies

Furthermore,in the case of φ = π,we will obtain that⟨a2⟩=0.Therefore,by appropriately choosing the parameters so that the condition in Eq.(9)is satisfied,we can make any of the cavities dark by tuning the phase difference φ.Under the condition in Eq.(9),the photonic intensity in each cavity can be expressed in a compact form as

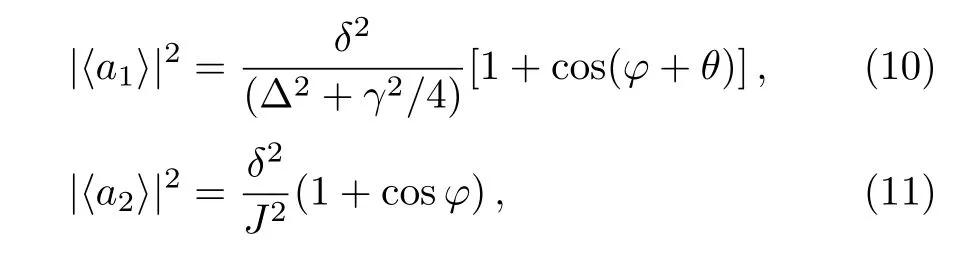
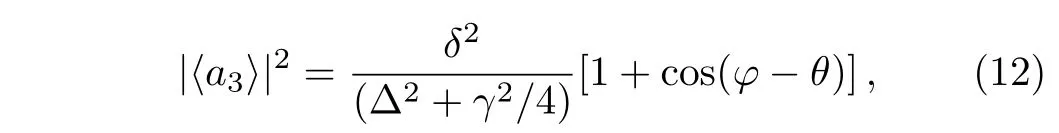
The phase dependence of steady state values in the case of∆ =2.773γ is shown in Fig.2,where we plot1,2,3)as a function of φ.It shows that,when φ = π,andwhen φ ≈ 0.8(1.2)π.In other words,we can realize the partially dark cavities in the trimer system,which is similar to that in optical molecule or dimer system.[18]However,as shown in Fig.2,when any of the cavities is dark with zero average photons in the steady state,the photonic intensities in the other two cavities can not achieve their maximum values.That is,we can not construct a perfect photonic flash.This defect can be overcome by driving the system resonantly,that is∆=0,in which situation we need a lossless condition γ′=0(whose realization will be discussed later)to guarantee the validity of Eq.(9).As a result,we will reach θ= π and the average photon number becomeand

Fig.2 The steady state values of the system as a function of the phase difference φ between two driving fields in the non-resonant driving situation.The parameters are set as J=2γ,λ =2γ,∆ =2.773γ,γ′=0.2γ.Under these parameters,the condition in Eq.(9)is satisfied.

Fig.3 The steady state values of the system as a function of the phase difference φ between two driving fields in the resonant driving situation.The parameters are set as J=0.5γ,λ =2γ,∆ =0,γ′=0.Under these parameters,the condition in Eq.(9)is satisfied.

In Fig.3,we plot the curve of the steady state values for ∆ =0.Therefore,when φ = π,we will haveandachieving their maximum values.On contrary,by adjusting φ =0(or 2π),the two side cavities in the trimer become completely dark,that isand the central cavity becomes bright.In Fig.3,we have chosen the inter-coupling strength as J=0.5γ,so that we will reach that the maximum values ofandare equal to each other.In such a way,we have constructed a perfect photonic flash only by tuning the phase difference in an optical trimer system.

4 Generalization to Coupled Cavity Array

The scheme of phase dependent photonic flash can also be naturally generalized to the system of N(>3)linearly coupled cavities.By driving the 1st and N-th cavities classically,the Hamiltonian of the system reads(in the rotating frame)

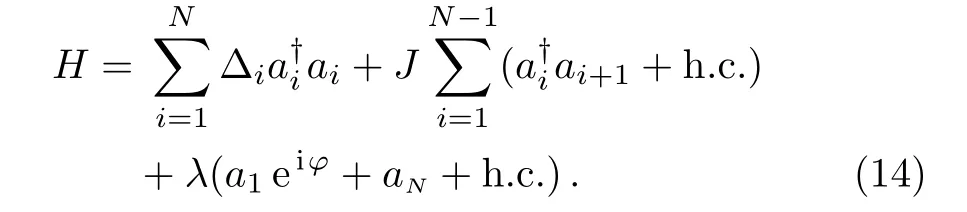
Motivated by the realization of perfect photonic flash in optical trimer structure,we here assume the resonant driving situation,and that all of the middle cavities are lossless by setting the parameters as∆i=0 and(γ >0,i=1,2,...,N).The Heisenberg-Langevin equation(neglecting the quantum noise)then reads

Firstly,let us consider the situation for odd N by assuming N=2m+1,where m is an integer.The steady state values can be obtained from Eq.(17)as

for j=1,2,...,m.It implies that,when cosφ = −(−1)m,all of the odd number cavities will be completely dark with zero intensity.Meanwhile,the photonic intensity in the even number cavities will achieve their maximums.The opposite event will occur as long as the phase difference satisfies cosφ =(−1)m,for which the even number cavities become dark and the odd ones become bright.In Fig.4(a),we illustrate the realization of photonic flash in an array of 5(m=2)coupled cavities.It shows that the even number cavities will be dark simultaneously(shown by the grey cavities)by tuning the phase difference such that φ=0,and they will turn bright(shown by the yellow cavities)when φ = π.At the same time,the odd number cavities will experience an exchange from bright ones to dark ones as we adjust the phase difference from φ=0 to φ=π.

Fig.4 (Color online)The scheme of phase dependent photonic flash based on coupled cavity array system.We take(a)N=5 and(b)N=6 as the examples for odd and even cavities,respectively.Here,we use the gray and yellow colors to represent dark and bright cavities respectively.

Secondly,let us move to the situation of even cavities,that is N=2m,where m is an integer.A simple calculation shows that the perfect photonic flash can be realized under the parameter γ=2J and the steady state values yield

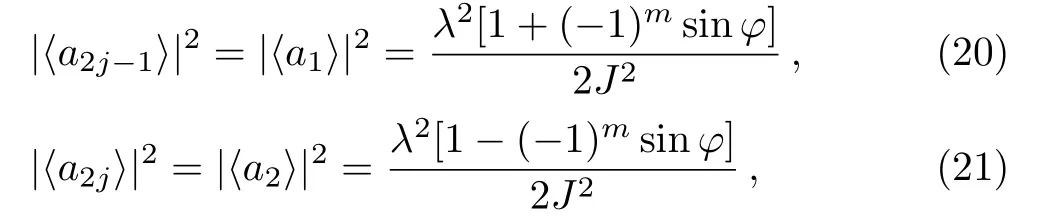
where j=1,2,...,m.Taking N=6(m=3)as an example,we illustrate the realization of perfect photonic flash in Fig.4(b).As shown in the figure,the odd(even)number cavities and even(odd)number cavities become bright(dark)alternatively when φ experiences a change from 3π/2 to π/2.

5 Remark and Conclusion

In this paper,we have investigated how to coherently control the steady state and realize the photonic flash in a coupled cavity array system.All of our discussions are based on the semi-classical approximation,where the decay of the side cavities are taken into consideration,but the effect of the noise is neglected.Here,the decay rates can be induced by for example the radiative loss and imperfectness of cavities and the noise mainly comes from the quantum fluctuation of the electromagnetic field in the surrounding environment.To go beyond the semi-classical approximation,the noise contribution to the photonic intensity in an optical trimer structure is obtained as

for i=1,2,3 and D(t)=exp(Mt).Hereis the average photon number by taking the quantum noise into account,M andare given in Eq.(3)and Eqs.(12),respectively.is the thermal photon number in the reservoir contacting with the j-th cavity.Therefore the quantum noise at zero temperaturewill make no contribution to the function of the photonic flash.Usually,the optical cavities are characterized by their high eigenfrequencies and the noise can be reasonably regarded as at zero temperature.Therefore,we believe that the semiclassical approximation in our discussion will give a logical prediction.

In conclusion,we have theoretically proposed a scheme for photonic flash based on linearly coupled cavity system by only tuning the phase difference between the two driving fields.We firstly demonstrate how to realize a partially dark optical trimer and then design a photonic flash,in which the side cavities are driven resonantly.In such a scheme,the side cavities achieve their vacuum steady state when the central one reaches a maximum photonic intensity,and vice versa.We also generalize the proposal of photonic flash to the system,which is composed of multiple coupled cavities,and show that the flash occurs between the odd and even number cavities.In our scheme,the middle cavities are required to be lossless,which can not be achieved strictly.However,within the current technologies,the decay rate can be negligibly small and satisfies our condition approximately.

At last,we claim that our proposal in this paper may be of potential application in the quantum device designing and quantum simulation.On one hand,in our current scheme,all of the cavities carry the same frequency,and a natural generalization is to design quantum neon.That is,the resonant frequencies of the cavities are different and so we can control the intensity of light with different“color” by adjusting the phase.On the other hand,since the cavities in our system can be dark or bright by tuning the phase difference,we here actually realize a control-lable photonic localization phenomenon. Traditionally,the localization is observed in the disordered nonlinear system,such as Anderson localization[29]and many-body localization.[30]We hope that our scheme in linear ordered cavity array system will be of potential application.

Acknowledgments

We thank D.L.Zhou and Y.X.Liu for their helpful discussions.