Energy Bounds for Static Spherically Symmetric Spacetime in f(R,G)Gravity
M.Farasat Shamir and Ayesha Komal
Department of Sciences and Humanities,National University of Computer and Emerging Sciences,Lahore Campus,Pakistan
AbstractThe main purpose of this paper is to investigate energy bounds in the context of f(R,G)gravity.To meet this aim,we choose static spherically symmetric spacetime in f(R,G)gravity to develop the field equations.We select three different models of f(R,G)gravity,which are thoroughly discussed in the literature.Firstly,the inequalities are formulated using energy bounds and then viability of the considered models are checked respectively.Graphical analysis show that specific f(R,G)gravity models are satisfied under suitable values of model parameters.It is shown that in a certain case energy bounds are satisfied expect SEC,which supports the late time acceleration expansion of unverse.
Key words:energy bounds,f(R,G)gravity
1 Introduction
Expansion of universe is a complicated and mysterious issue in cosmology.[1]Positive energy densities are one of the crucial lineaments of the models of the universe with usual matter.In other words,the components of energy momentum tensor when written in different linear combinations,they should be non-negative or positive.A linear function of Ricci scalar in the gravitational Lagrangian density was adopted to drive the Einstein field equation from Hilbert action by considering higher order curvature invariant in the gravitational Lagrangian density.[2−3]However,the approach may be generalized by considering f(R)gravity.
Energy conditions can be used to discuss many significant and valuable aspects like Hawking-Penrose singularity theorems and the validity of second law of black hole thermodynamics.[4]We may categorize them as the null energy condition(NEC),weak energy condition(WEC),strong energy condition(SEC)and dominant energy condition(DEC).The stability and viability of cosmological models in f(R)gravity has been investigated using energy conditions.[5]Cosmic expansion is indicated by the violation of SEC in context of modified gravity.[6]Shamir[7]discussed power law anisotropic f(R)cosmology and tested energy conditions.Santos et al.[8]evaluated energy conditions and particularly explained the NEC using Raychaudhri metric in f(R)and f(R,G)gravity. Barart and Vagenas[9]studied charged black hole metric to get the satisfactory results using WEC.Bertolami and Sequeira[10]also worked on energy conditions to explore the stability and viability of cosmological models in f(R,G)gravity.Atazadeh and Darabi[11]determined WEC in f(R,G)gravity with help of experimental values of cosmological parameters.Alvarenga et al.[12]studied energy conditions in modified gravity f(R,T)and also discussed properties of de-sitter solution like perturbations and stabilities etc.Shamir[13]discussed energy conditions in modified theory of gravity in the light of anisotropic background.Sharif and Ayesha[14]analyzed energy conditions in f(G,T)gravity and achieved realistic constraints on free parameters for Friedmann-Robertson-Walker(FRW)model.Garcia el al.[15]examined energy conditions for FRW model and also tested the viability of modified Guass-Bonnet gravity model.Yang[16]explored violation of the WEC with reference to equation of state using the inflationary Yang-Mills condensate. Thus it seems interesting to investigate energy condition in modified gravity.
This article investigates energy conditions in the context of f(R,G)gravity.For this purpose,static spherically symmetric model is considered.The article comprises of two portions.In the first half of document is used to develop the field of f(R,G)gravity.In the second half inequalities which correspond to the energy conditions are given.Later on,by taking three different models of f(R,G)gravity the constraints resulting from the energy conditions are analyzed.The last part of paper concludes the whole work.
2 Modified Field Equations
The action for f(R,G)gravity is given below

where SM(gµν,ψ)is the matter action,R is Ricci scalar and G is Guass-Bonnet invariant de fined as
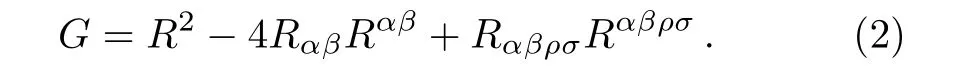
Here Rαβand Rαβρσare notations employed for the Ricci and Riemann tensors respectively.The following gravita-tional field equations are obtained by varying the action(1)with respect to metric tensor
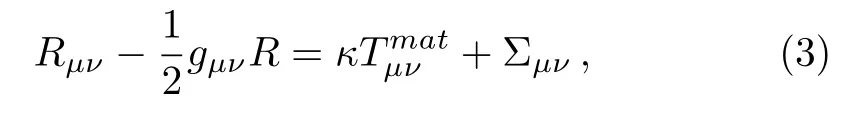
where
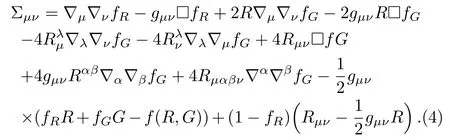
Here∇µis the covariant derivative,fRand fGdenote partial derivatives with respect to R and G respectively.For the present work,we consider static spherically symmetric metric of the form[17]
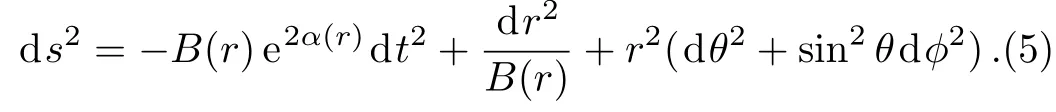
The values of R and G for the above spacetime turn out to be

where the prime denotes the derivative with respect to radial coordinate.The stress energy tensor is de fined as
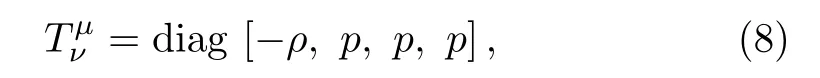
where the energy density ρ and pressure p are also functions of radial coordinate.Using Eqs.(3),(5),and(8),we obtain the following set of differential equations
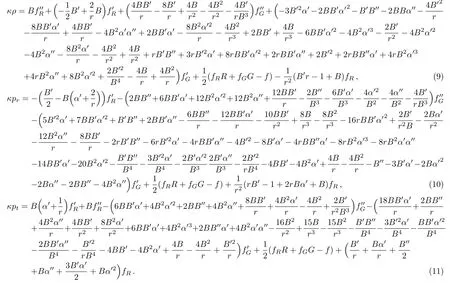
It is mentioned here that these are highly non-linear and complicated equations to deal with.
3 Energy Conditions and Graphical Analysis
Important theorems about black holes may be established using the energy conditions.A linkage between energy conditions and viability of some specific cosmological models has been observed considerably in the recent literature.For the expansion of universe,the energy conditions are reflected by the term Rµνυµυν≥ 0 in the Raychaudhuri equation

where ωµν, σµν,and θ represent the rotation,shear and expansion respectively.Four different categories of energy conditions i.e.NEC,WEC,SEC,and DEC are given by[18]

where prand ptrepresent the radial and tangential pressure components respectively.The details of calculations to investigate these energy conditions are shown in Eqs.(19)–(23)in Appendix section.We consider three well known choices of f(R,G)models[19]

3.1 f1(R,G)=k1RβGγ
Due to the long and complex nature of equations,the exact analytical expressions for specific parameter range of β,γ,and r can not be written here.For graphical analysis,we assign the parameter ranges for β,r,and the value of γ are fixed(γ = −3).For model f1(R,G),it is clear from Figs.1–3 that all energy conditions are satisfied for the given range of parameters β and r.

Fig.1 Plots of NEC and WEC for model f1(R,G)=k1RβGγ.

Fig.2 Plots of SEC for model f1(R,G)=k1RβGγ.

Fig.3 Plots of DEC for model f1(R,G)=k1RβGγ.
Moreover,a tabular description for violation and obeying of energy conditions with different parameters is also shown in Tables 1–3.

Table 1 Behavior of model with fixed k1and β.

Table 2 Behavior of model with fixed k1and γ.

Table 3 Behavior of model with fixed β and γ.
3.2 f2(R,G)=k2R+k3RnGm
The graphical results of energy conditions for the model f2(R,G)are shown in Figs.4–6 with the specific range of parameter n and by fixing other parameters.
For this model,a detailed tabular description of energy conditions with different parameters is shown in Tables 4–8.

Fig.4 Plots of NEC and WEC for model f2(R,G)=k2R+k3RnGm.

Fig.5 Plots of NEC and WEC for model f2(R,G)=k2R+k3RnGm.
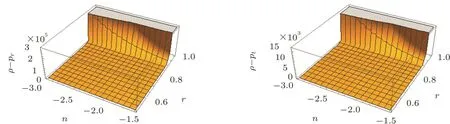
Fig.6 Plots of NEC and WEC for model f2(R,G)=k2R+k3RnGm.

Table 4 Behavior of model with fixed k3and m.

Table 6 Behavior of model with fixed m and n.

Table 7 Behavior of model with fixed k4and m.
3.3 f3(R,G)=k4RnG(1−m)
Here range is assigned to the parameter n and m is fixed(m=−2)for the graphical analysis.For this model,NEC,WEC,SEC,and DEC are satisfied for the given range(See Figs.7–9).Table 9 shows the validity of energy conditions for some fix values of parameters m and n.
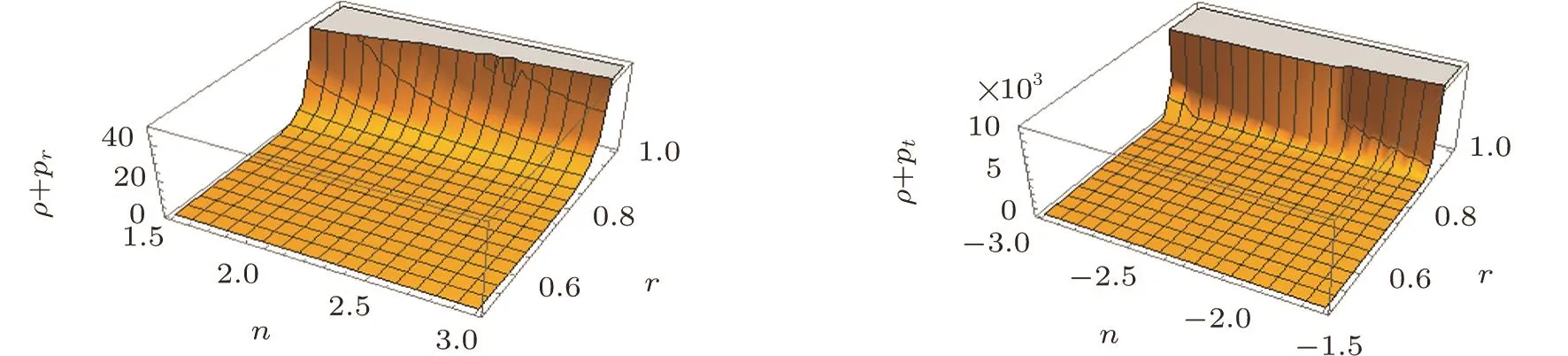
Fig.7 Plots of NEC and WEC for model f3(R,G)=k4R+RnG1−m.

Fig.8 Plots of SEC for model f3(R,G)=k4RnG1−m.

Fig.9 Plots of DEC for model f3(R,G)=k4RnG1−m.

Table 9 Behavior of model with fixed m and n.
4 Conclusion
In this paper,the f(R,G)gravitational theory is explored in the light of energy conditions.We have considered static spherically symmetric spacetime for the present analysis. We have studied three well known f(R,G)gravity models.[19]Moreover,due to highly nonlinear and complicated nature of the gravitational field equations,we take Schwarzschild like geometry and consider B=1−(2M/r)and α =c1r+c2where M represents the mass of star and c1,c2are the arbitrary constants.
Further,we accept the vacuum case for the investigation as it has been contended that the steadiness of the cosmological arrangements utilizing viability conditions can be defended by picking some precise decisions of model parameters.[11,19]Additionally the general outcomes do not change and without the loss of generality the pressure and positive energy density may likewise be added to fulfill the viability conditions.All four forms of energy conditions are graphically discussed in detail for the three f(R,G)gravity models.
The fundamental aspect of this work is the 3-dimensional examination in which some model parameters are settled and the outcomes are analyzed by changing alternate parameters.The work can be further extended by changing the parameters used in the present investigation and furthermore by considering some other f(R,G)gravity models.
Appendix

 Communications in Theoretical Physics2018年8期
Communications in Theoretical Physics2018年8期
- Communications in Theoretical Physics的其它文章
- Effect of Critical Beam Radius on Self-focusing of cosh-Gaussian Laser Beams in Collisionless Magnetized Plasma
- Spherical Gravitational Collapse in f(R)Gravity with Linear Equation of State
- Self-Similar Solution of Spherical Shock Wave Propagation in a Mixture of a Gas and Small Solid Particles with Increasing Energy under the Influence of Gravitational Field and Monochromatic Radiation
- Jeans Instability of Self Gravitating Dust Cloud in Presence of Effective Electrostatic Pressure
- Phase Sensitive Photonic Flash∗
- Effects of Thermal Radiation on a 3D Sisko Fluid over a Porous Medium Using Cattaneo-Christov Heat Flux Model∗
