Effect of Critical Beam Radius on Self-focusing of cosh-Gaussian Laser Beams in Collisionless Magnetized Plasma
T.U.Urunkar, S.D.Patil, A.T.Valkunde, B.D.Vhanmore, K.M.Gavade, and M.V.Takale
1Department of Physics,Shivaji University,Kolhapur 416 004,India
2Department of Physics,Devchand College,Arjunnagar,Kolhapur 591 237,India
AbstractEffect of critical beam radius on self-focusing of cosh-Gaussian laser beams in collisionless magnetized plasma under ponderomotive nonlinearity forms the main core of present work.To investigate propagation dynamics of cosh-Gaussian laser beams in collisionless magnetized plasma,well established parabolic equation approach under WKB and paraxial approximations is employed.Our study is crucially pivoted on the concept of critical curve and subsequent determination of numerical interval for decentered parameter to sustain the competition between diffraction and self-focusing during the propagation of laser beam.Additionally,in the present study an interesting feature in the self-focusing region of the critical curve has been attempted for different values of decentered parameter.
Key words:self-focusing,cosh-Gaussian,magnetized plasma,beam radius,decentered parameter
1 Introduction
Understanding the propagation dynamics of intense laser beam through plasma is essential due to its wide range of applications,such as inertial confinement fusion,[1−2]laser based electron acceleration,[3−4]ionospheric modification,[5]x-ray lasers,[6]harmonic generation[7−8]etc.Above stated applications need laser beam to propagate over several Rayleigh lengths in plasma without loss of energy.When an intense laser beam propagates through plasma,it exerts ponderomotive force on electrons.This force can give rise to various nonlinear effects[9−11]in laser-plasma interaction,such as stimulated Raman scattering,resonance absorption,magnetic field generation,self-focusing etc.Among above stated effects,phenomenon of self-focusing plays a crucial role in propagation dynamics of the beam.Phenomenon of selffocusing arises due to increase of the axial refractive index as compare to the peripheral of the laser beam.[12]
Early analyses on propagation dynamics of laser beams have been reported by Akhmanov et al.[13]for nonlinear medium and further developed by Sodha et al.[14]for plasmas by considering different nonlinear mechanisms.In past,the analyses[15−16]on propagation of Gaussian laser beam in plasmas characterise and differentiates the nature of beam propagation in three distinct regimes.Such propagation regimes include steady divergence,oscillatory divergence and self focusing of laser beams.Under the consideration of such regimes of interaction,several theoretical investigations on self-focusing of Gaussian laser beam[17−19]in plasmas have been reported.Recently,a great interest has been evinced in production and propagation of decentred Gaussian beams,usually known as cosh-Gaussian beams on account of their wide range of applications.The propagation properties of cosh-Gaussian laser beams are important for its technological interest as these beams possess high power in comparison to that of a Gaussian beam.[20]As such,the propagation of cosh-Gaussian laser beams in plasmas under different situations has been studied in detail.[21−22]
In present paper,authors have given a lucid analytical treatment to study effect of critical beam radius on self-focusing of cosh-Gaussian laser beams in collisionless magnetized plasma.The organization of the paper is as follows:Section 2 gives the evolution of beam-width parameter equation.Discussion of results in context of selffocusing of Gaussian beam is elaborated in Sec.3.Finally,a brief conclusion is added in Sec.4.
2 Theoretical Framework
Let us consider the propagation of cosh Gaussian laser beam through a collisionless magnetized plasma along the z direction in which static magnetic field B0is applied.The electric field of the laser beam propagating in either modes i.e.in extraordinary and ordinary modes can be written as,[23]

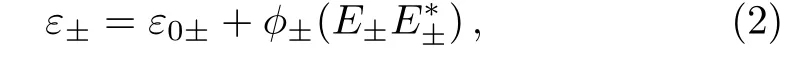
where ε0±andare the linear and nonlinear parts of the dielectric constant of collisionless magnetized plasma and can be expressed as,

In the light of Maxwells elctrodynamic equations in esu system,the general form of wave equation governing the propagation of laser beam is given as,

where
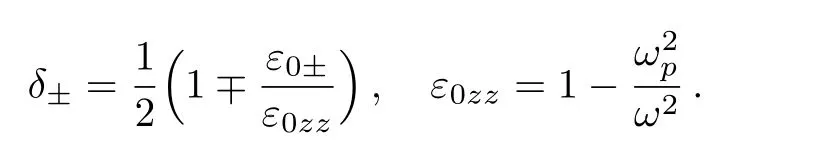
The electric field E±given by Eq.(1)satisfies Eq.(5).In circular cylindrical coordinate system,under slowly varying envelope approximation,the evolution of electric field envelope in collisionless magnetized plasma can be expressed as,

In WKB approximation one can neglect∂2E/∂z2from Eq.(5).The complex amplitude of electric vector may be expressed as,


Following approach given by Akhmanov et al.[13]and developed by Sodha et al.[14]the solution of Eqs.(8)and(9)for cosh Gaussian laser beam can be written as,



where,

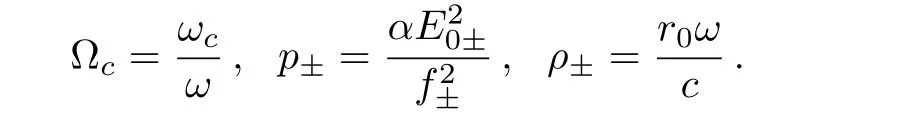
3 Results and Discussions
Equation(13)is the second order nonlinear differential equation,which represents variation of beam width parameterwith normalized distance of propagationThe first term on the right-hand side of this equations corresponds to the diffraction divergence of the beam and the second term corresponds to the convergence resulting from the nonlinearity in dielectric constant of collisionless magnetized plasma.
We have made analytical investigations to sustain competition between the two terms on right-hand side of Eq.(13)from which one may obtain the critical curve equation as below,

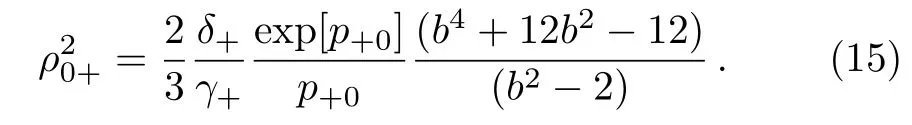
Equation(15)is significant equation,which throws light on condition for self trapping of laser beam,for following analysis one may show that self trapping is determined by critical power but it is also determined by corrosponding ρ0+min.Therefore following the same line of analysis,[24]one may determine ρ0+minanalytically as,
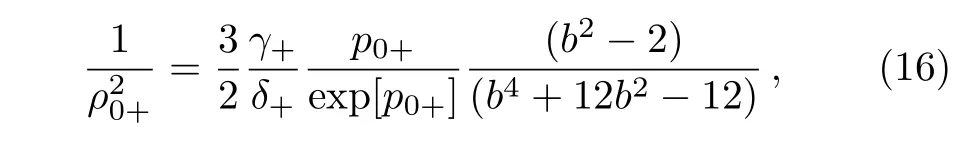

Solving this equation one obtains p0+=1.Putting this value in Eq.(16)we get,
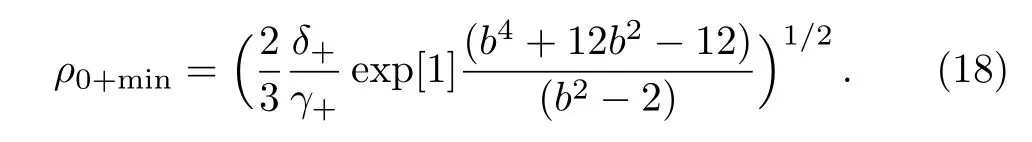
By using de fining equations for δ+and γ+given previously and numerical values N0=1×1018cm−3,ω =1.776×1015rad/S,B0=106gauss in Eq.(17)becomes,

From Eq.(19)it is seen that ρ0+minis purely b dependent.By using numerical computation under the condition that ρ0+min>0 one may obtain domain of decentered parameter in between 0≤b≤0.9634.Figure 1 gives plot between ρ0+minversus b.

Fig.1 Variation of ρ0+minwith decentered parameter b.
The critical curve is plotted from Eq.(15)by using values of decentered parameter b from above de fined domain,which is shown in Fig.2.From Fig.2 it is seen that the critical curve shift towards minimum value of ρ0+with increase in value of b.
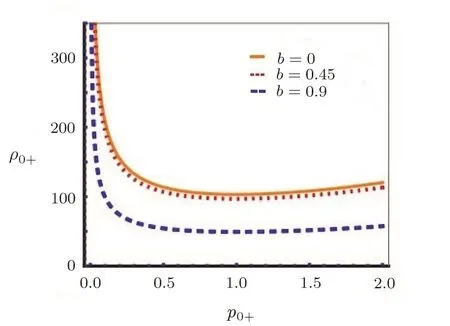
Fig.2 Critical curves for various b values.
Intially at ξ+=0 and f+=1 the left-hand side of Eq.(13)becomes zero and the right-hand side of Eq.(13)is represented by functionwith b as a parameter having values 0,0.45,0.9.The function F in following Eq.(20)is basically differential equation,to study its variation with ρ0+min,it is de fined to be depending upon ρ0+min.

Equation(20)is purely dependent on ρ0+min.The function F(p0+=1,ρ0min)vanishes if the initial beam power,critical beam radius pointfalls on the critical curve,the functionhas a negative value if the pointfalls above the critical curve and a positive value if the pointfalls below the critical curve.For this result the graph ofversus ρ0+minis plotted from Eq.(20)for given values of decentered parameter b as shown in Fig.3.From Fig.3.the regions for well known nonlinear phenomena such as self trapping,self-focusing and defocusing are observed forandrespectively.From Fig.3.the ranges of ρ0+minfor these nonlinear phenomena can be found out and these ranges are as follows:
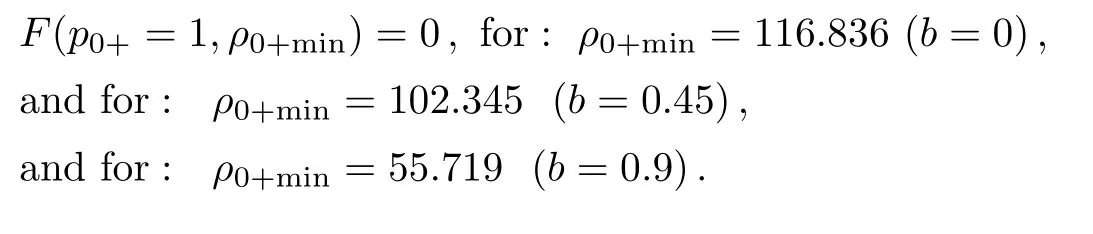
The above stated values of ρ0+minare for the selftrapping condition,so beam pass through the collisionless magnetized plasma without any deviation.

In this range of ρ0+minself-focusing is observed.

In this range of ρ0+mindefocusing is observed.

Fig.3 Variation of F(p0+=1,ρ0+min)with ρ0+minfor given values of decentered parameter b.
The interest of present study is in self-focusing region.From Fig.3 it is seen that in self-focusing region the three curves intersects each other at three different points called turning points,these points can be calculated analytically and graphically as shown in inset of Fig.3.
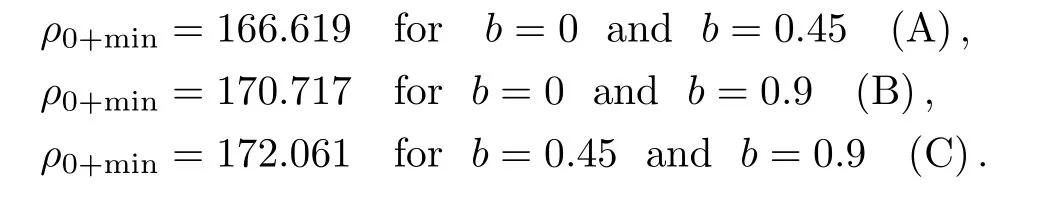

Fig.4 (Color online)Dependence of the extraordinary beam-width parameter f+on the dimensionless propagation distance ξ+in collisionless magnetized plasma,at ρ0+min=120 and p0+=1.
From Fig.3 it is clear that at the turning points,for a given ρ0+min,there can be two distinct values of decentered parameter b are possible,which gives the identical F(p0+=1,ρ0+min)value or one may also say that there can be two distinct beam width differential equation for two distinct values of decentered parameter b such that the evolution of laser beam would be identical.The above significance of graph is also evident from the Eq.(20)itself.
Due to these turning points the self-focusing region is sub-divided into two regions region I and region II.The graph of beam width parameter f+versus normalized propagation distance ξ+is plotted from Eq.(13)for given values of decentered parameter b by taking value of ρ0+minfrom region I(ρ0+min=120)and region II(ρ0+min=320)as shown in Figs.4 and 5.respectively.
From Fig.4 it is seen in region I,enhanced self-focusing is observed with reduction in self-focusing length.The exact reverse behaviour with increase in self-focusing length is observed with enhanced self-focusing in region II as shown in Fig.5.

Fig.5 (Color online)Dependence of the extraordinary beam-width parameter f+on the dimensionless propagation distance ξ+in magnetized plasma at ρ0+min=320 and p0+=1.
4 Conclusion
We have investigated the domain of value of decentered parameter b for ρ0+minis positive.By using values of b from this domain we see the effect of b on critical curve.Following important conclusions are obtained from present analysis:
(i)Critical Minimum beam radius decreases with increase in decentered parameter values.
(ii) (p0+,ρ0+)point shift towards defocusing region with increase in decentered parameter values.
(iii)Self-focusing length based on turning point critical beam radius is observed.
 Communications in Theoretical Physics2018年8期
Communications in Theoretical Physics2018年8期
- Communications in Theoretical Physics的其它文章
- A Numerical Investigation of Nanocomposite of Copper and Titanium Dioxide in Water Based Fluid Influenced by Instigated Magnetic Region
- Effects of Thermal Radiation on a 3D Sisko Fluid over a Porous Medium Using Cattaneo-Christov Heat Flux Model∗
- Energy Transfer in the Light-Harvesting Complexes of Purple Bacteria∗
- Phase Sensitive Photonic Flash∗
- Jeans Instability of Self Gravitating Dust Cloud in Presence of Effective Electrostatic Pressure
- Self-Similar Solution of Spherical Shock Wave Propagation in a Mixture of a Gas and Small Solid Particles with Increasing Energy under the Influence of Gravitational Field and Monochromatic Radiation
