Effects of Thermal Radiation on a 3D Sisko Fluid over a Porous Medium Using Cattaneo-Christov Heat Flux Model∗

Deog-Hee Doh,M.Muthtamilselvan,E.Ramya,and P.Revathi

1Department of Mathematics,Bharathiar University,Coimbatore-641 046,Tamilnadu,India

2Division of Mechanical Engineering,College of Engineering,Korea Maritime and Ocean University,Busan 606 791,South Korea

AbstractThis paper investigates the three-dimensional flow of a Sisko fluid over a bidirectional stretching sheet,in a porous medium.By using the effect of Cattaneo-Christov heat flux model,heat transfer analysis is illustrated.Using similarity transformation the governing partial differential equations are transferred into a system of ordinary differential equations that are solved numerically by applying Nachtsheim-Swigert shooting iteration technique along with the 6-th order Runge-Kutta integration scheme.The effect of various physical parameters such as Sisko fluid,ratio parameter,thermal conductivity,porous medium,radiation parameter,Brownian motion,thermophoresis,Prandtl number,and Lewis number are graphically represented.

Key words:Sisko fluid,Cattaneo-Christov heat flux model,thermal radiation,porous medium

1 Introduction

Most of the studies described the flow of viscous fluid by using classical Newtonian model.The greater part of the fluids in industry does not hold frequently established supposition of a linear relationship amongst stress and rate of strain and consequently described as non-Newtonian fluids. Biological fluids,Polymeric liquids,lubricating oils,liquid crystals,drilling mud and paints are the rheological complex fluids,which has vescoelastic manner and cannot be represented just as Newtonian fluids.The non-Newtonian fluid flow is usually more complex and particularly non-linear,this may get more troubles utilizing numerical methods to concentrate on such flows are investigated by Neofytou.[1]Nadeem et al.[2]studied the cause of nanoparticles for Jeffrey fluid flow over a stretching sheet.Sajid and Hayat[3]exhibited an examination to research the wire covering investigation of Siskofluid withdrawal from a bath.Wang et al.[4]discussed for the MHD peristaltic flow qualities of a Sisko fluid in a symmetric or asymmetric channel.

Khan et al.[5]investigated the 3-D Sisko fluid flow over a bidirectional stretching surface with Cattaneo-Christov heat flux model.They concluded that the concentration dissemination was reduced with the improvement of the heterogeneous and homogeneous reactions in both case of shear thickening and shear thinning fluids.Molati et al.[6]discussed on the unidirectional incompressible MHD flow of a Sisko fluid.Akyildiz et al.[7]focussed the thin film flow of a Sisko fluid on a moving belt.The outcomes obtained reveals many interesting conducts that warrant investigation of the conditions identified with non-Newtonian fluid phenomena,particularly the shear-thinning phenomena.Shear-thinning lessens the wall shear stress.Hayat et al.[8]investigated the effect of nanoparticles and magnetic field in the 3D flow of Sisko fluid.The flow is caused by a bidirectional stretching sheet.Valipoura et al.[9]examined the Buongiorno Model is applied for melting heat transfer effect on nanofluid heat transfer intensification between two horizontal parallel plates in a rotating system.

Many applications in engineering disciplines involve high permeability porous media.In such situation,Darcy equation fails to give satisfactory results.Therefore,use of non-Darcy models,which takes care of boundary and inertia effects,is of fundamental and practical interest to obtain accurate results for high permeability porous media.Khan et al.[10]presented the numerical solutions for the flow of an MHD Sisko fluid past a porous medium.A hypothetical non-linear model for the move through a porous medium has been produced by utilizing modified Darcy’s law.Sheikholeslami and Ganji[11]exhibited twodimensional laminar constrained convection nanofluid flow through a stretching porous surface.Doh et al.[12]studied the transient heat and mass transfer flow of a micropolar fluid between porous vertical channel with boundary conditions of third kind.Recently,various researcher published papers about the nanofluid flow through a porous mediam.[13−20]

In matter thermal motion of charge particles generate an electromagnetic radiation is denoted as thermal radiation.Some fields of applications are Medicine,X-ray,radiography,food safety and smoke detector.Hayat et al.[21]examined the effect of warm radiation on peristaltic transport of nanofluid in a channel with convective limit conditions.Zeeshan et al.[22]investigated the effects of heat transfer and thermal radiation on the flow of ferro-magnetic fluid on a stretching surface.Bhatti and Rashidi[23]acquired the impact of thermo-diffusion and thermal radiation on Williamson nanofluid past a permeable stretching/shrinking surface.Majeed et al.[24]considered two-dimensional heat transfer of unsteady ferromagnetic liquid and boundary layer flow of magnetic dipole with given heat flux.Akbar et al.[25]analyzed the peristaltic consistent of three diverse nanoparticles with water as base liquid affected by slip boundary conditions through a vertical asymmetric porous channel within the presence of MHD.Waqas et al.[26]studied the characteristics of generalized Burgers fluid over a stretched surface by using Cattaneo-Christov heat flux model.Malik et al.[27]investigated the convective flow of Sisko fluid with the thought of Cattaneo-Christov heat flux model and thermal relaxation time.Liu et al.[28]explored the time and space partial Cattaneo-Christov constitutive model to portray heat conduction.Hayat et al.[29]addressed about the stagnation point stream of Jeffrey liquid towards a stretching cylinder.

In the current study,the flow of three-dimensional Sisko fluid past in a porous medium is considered.Here the Brownian motion and thermophoresis are taken into account. By using the similarity transformation,the partial differential equations are reduced to ordinary differential equations are solved numerically by applying Nachsheim-swigert shooting iteration technique along with the 6-th order Runge-Kutta integration scheme.The effects of various physical parameters on the velocity,temperature and concentration are graphically represented.

2 Mathematical Formulatio n

We consider the steady three-dimentional layer flow of an incompressible Sisko fluid past a porous medium which is outlined in Fig.1.The sheet is thought to be stretched along x and y-directions with linear velocities u=cx and v=dy respectively,where c,d>0 are the stretching rates and flow happens in the space z>0.Radiation,Brownian motion and thermophoresis effects are also there.The boundary layer equations governing the three dimensional Sisko fluid with heat and mass transfer are expressed below,[5]

where u=Uw(x),v=Vw(y)=dy,w=0,T=Tw,

then

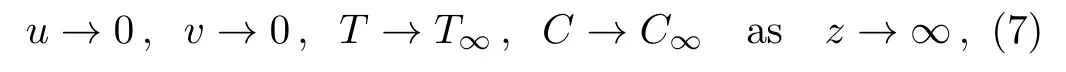
where the velocity components are(u,v,w)in the x,y,and z directions respectively,the material constant of the Sisko fluid is(a,b,n≥0)represents the shear rate viscosity,consistency index and power-law index respectively.Involvement of power index n provides an edge to Siskofluid as shear thinning(n<1),shear thickening(n>1),the temperature T,the ratio diffusion coefficient δE,the density of the base fluid ρfwith the specific heat of fluid at constant temperature cf.

Fig.1 Schematic diagram of the problem.

The thermal conductivity of the fluid is assumed to vary linearly with temperature as,

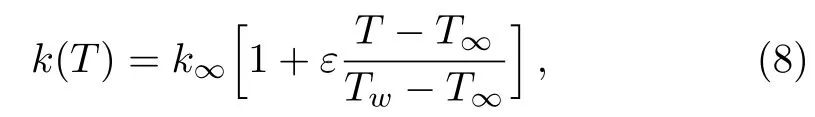
where k∞signifies the thermal conductivity of the fluid far from the sheet surface and ε is a small parameter known as the thermal conductivity parameter.

We now use the following dimensionless variables

Making use of the transformations(Eq.(9)),(Eq.(1))is identically satisfied and Eqs.(2)–(7),having in mind Eq.(8),leads to the following forms

From the above equations,prime denotes the differentiation with respect to η,the material parameter of Siskofluid is A,the porous medium is K,the local Reynolds numbers are denoted as Reaand Reb,the radiation parameter is denoted as R,the generalized Prandtl number is Pr,the stretching ratio parameter is α,the relaxation time of the heat flux is denoted as λE,the thermophorosis parameter is denoted as Nt,the Brownian motion is de-noted as Nb,the Lewis number is denoted as Le.These parameters are stated as follows,

Local Nusselt number and skin friction coefficients are given by,

It is noted that the dimensionless mass flux represented by the Sherwood number Shxis identically zero.

3 Numerical Solution

The nonlinear ordinary differential Eqs.(10)–(13)with the boundary conditions in Eqs.(14)–(15)are solved numerically by using Runge-kutta method along with Nachtheim-Swigert shooting iteration technique.According to the major requirements of this numerical method,the main steps of the technique are given as follows.[5]

Let,

and the boundary conditions become

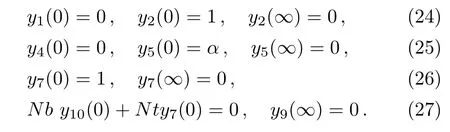
4 Numerical Results and Discussion

The predominant focus of this article is to analyze the characteristics of Cattaneo-Christov heat flux model for the Sisko fluid flow past a porous medium.The effect of various physical parameters like stretching ratio parameter(α =0.0 to 1.5)taken as α =0 and α =1 that represent the unidirectional and axisymmetric stretching,Sisko fluid(A=0.0 to 1.5),thermal conductivity parameter(ϵ=0.0 to 1.5),porous medium(K=0.0 to 1.5),radiation parameter(R=0.0 to 1.5),Brownian motion(Nb=0.1 to 1.5),thermophoresis parameter(Nt=0.1 to 1.5)chosen as Nt<0 and Nt>0 that physically represent the heated and cold surface respectively,Prandtl number(Pr=0.1 to 1.7)taken as Pr>0 that represent the oils,relaxation time of the heat transfer(λE=0.0 to 0.3)and Lewis number(Le=0.1 to 1.5)on a dimensionless velocities f′(η),g′(η),temperature distribution θ(η)and concentration distribution ϕ(η)are studied numerically.

Fig.2 Comparative study of velocity profiles for different values of Sisko fluid A.

The effect of different values of Sisko fluid A is compared with the present study and the previous study of Khan et al.[5]and better agreement is found. This is shown in Fig.2.Effect of Sisko fluid parameter A on the velocity profiles f′(η),g′(η),temperature θ(η)and concentration ϕ(η)distributions are plotted in Figs.3–6 respectively.Here the velocity profiles f′(η),g′(η)are increased,at the same time the temperature and concentration profiles are decreased,when the Sisko fluid parameter A is increased.Here increment in Sisko fluid parameter towards a low viscosity at high shear rate,leads to a decline in both temperature and concentration profiles and the related boundary layer thickness.

Fig.3 Velocity profile f′(η)for different value of Siskofluid A.

Fig.4 Velocity profile g′(η)for different value of Siskofluid A.

Fig.5 Temperature profile θ(η)for different values of Sisko fluid A.

Figures 7–10 present the variations in the velocities f′(η),g′(η),temperature θ(η)and concentration ϕ(η)distributions for different values of ratio parameter α.When the ratio parameter α is increased,the velocity profiles increases and temperature and concentration profiles decreases.

Fig.6 Concentration profile ϕ(η)for different values of Sisko fluid A.

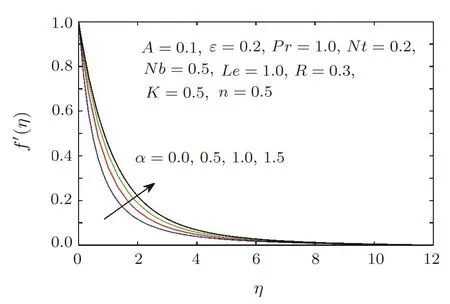
Fig.7 Velocity profile f′(η)for different values of the stretching ratio parameter α.

Fig.8 Velocity profile g′(η)for different values of the stretching ratio parameter α.

Through Figs.11–12,the enhancement of temperature θ(η)and concentration ϕ(η)profiles are shown for the higher values of thermal conductivity parameter ϵ.This increase is a direct result of thermal conductivity of the fluids for higher values of the small scalar parameter ϵ arisen in the variable thermal conductivity.In addition,more heat is transferred from sheet to the liquid and eventually the temperature dispersion is expanded.

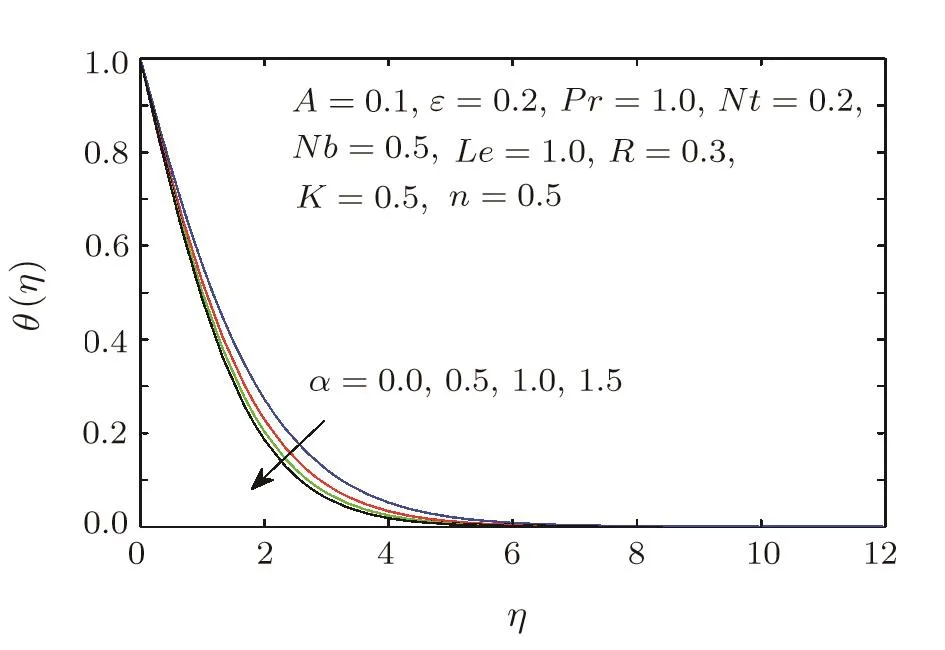
Fig.9 Temperature profile θ(η)for different values of stretching ratio parameter α.

Fig.10 Concentration profile ϕ(η)for the different values of stretching ratio parameter α.

Fig.11 Temperature profile θ(η)for different values of thermal conductivity parameter ϵ.

The porous medium K on the velocity,temperature θ(η)and concentration ϕ(η)distributions are plotted in Figs.13–16 respectively.The increment of the porous medium give rise to the increment in the temperature,concentration and boundary layer thickness,but the velocity profiles f′(η)and g′(η)are reduced.Figures 17–18 depict an enhancement behaviour of the temperature and concentration profiles and their boundary layer,for larger values of the radiation parameter R.For large values of radiation parameter,generates a significant amount of heating to the Sisko fluid,which enhances the Sisko fluid temperature and concentration boundary layer thickness.Figures 19–20 display that the temperature θ(η),concentration ϕ(η)and boundary layer thickness drops when the Prandtl number is increased.

Fig.12 Concentration profile ϕ(η)for the different values of thermal condutivity parameter ϵ.

Fig.13 Velocity profile f′(η)for different values of the porous medium K.

Fig.14 Velocity profile g′(η)for different values of the porous medium K.

The temperature and concentration profiles of the Sisko fluid flow are seen to decrease with the addition of thermal relaxation parameter λEas depicted in Figs.21–22.In a physical sense,additional time is important for the heat transfer for molecule to molecule of the liquid.In the result,the temperature and concentration boundary layer are diminished in the Sisko fluids.Moreover,for λE=0,that is for traditional Fourier’s law,where the temperature is higher when contrasted with the Cattaneo-Christov model.This is because of heat transfer through material right away.

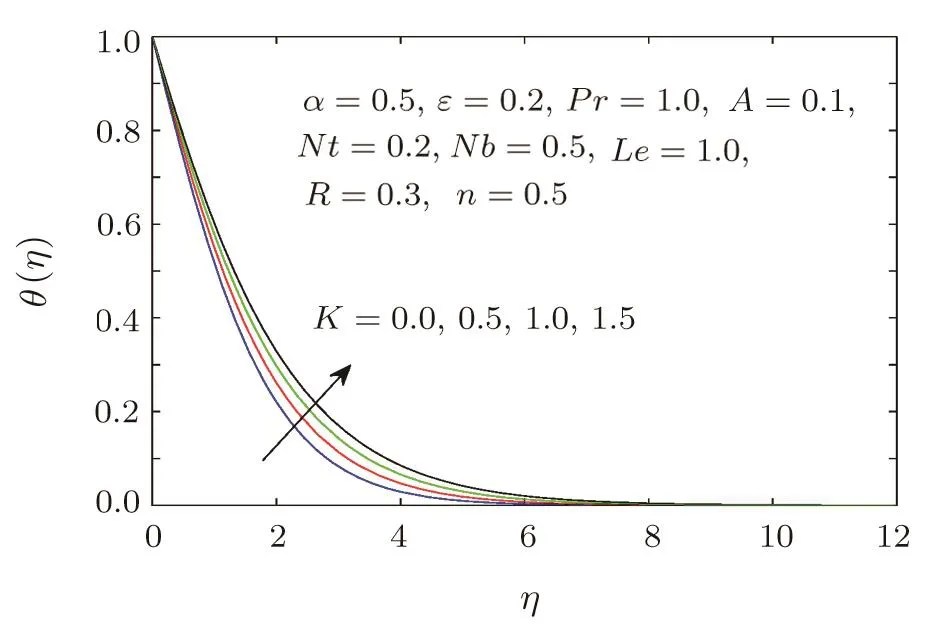
Fig.15 Temperature profile θ(η)for different values of porous medium K.

Fig.16 Concentration profile ϕ(η)for different values of porous medium K.

Fig.17 Temperature profile θ(η)for different values of radiation parameter R.

Figure 23 shows the effect of the Brownian motion parameter Nb on the concentration ϕ(η)profile.Here increase in the Brownian motion parameter leads to the decrease in the concentration profile.Generally,for higher values of Brownian motion have a tendency to heat the fluid in the boundary layer,due to this seen that declines in the concentration profile.

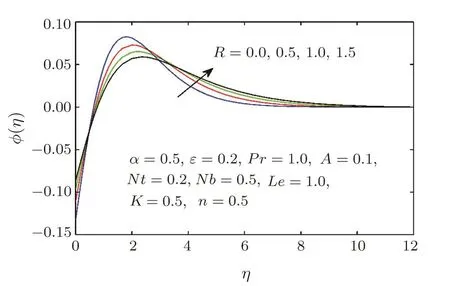
Fig.18 Concentration profile ϕ(η)for different values of radiation parameter R.

Fig.19 Temperture profile θ(η)for different values of Prandtl number Pr

Fig.20 Concentration profile ϕ(η)for different values of Prandtl number Pr.

Figure 24 describes the influence of thermophoresis parameter Nt on the concentration profile ϕ(η).When the thermophoresis parameter increases,the concentration profile is also increases.Generally,improving the values of thermophoresis parameter generates a force leads to move the particles from the hotter region to the colder regions for which there is a gain in the heat transfer rates.

Fig.21 Temperture profile θ(η)for different values of the relaxation time parameter λE.

Fig.22 Concentration profile ϕ(η)for different values of the relaxation time parameter λE.

Fig.23 Concentration profile ϕ(η)for different values of Brownian motion Nb.

Figure 25 describes the impact of Lewis number Le on the concentration profile ϕ(η).It shows that the higher values of Lewis number Le causes a decrease in the concentration distribution ϕ(η).

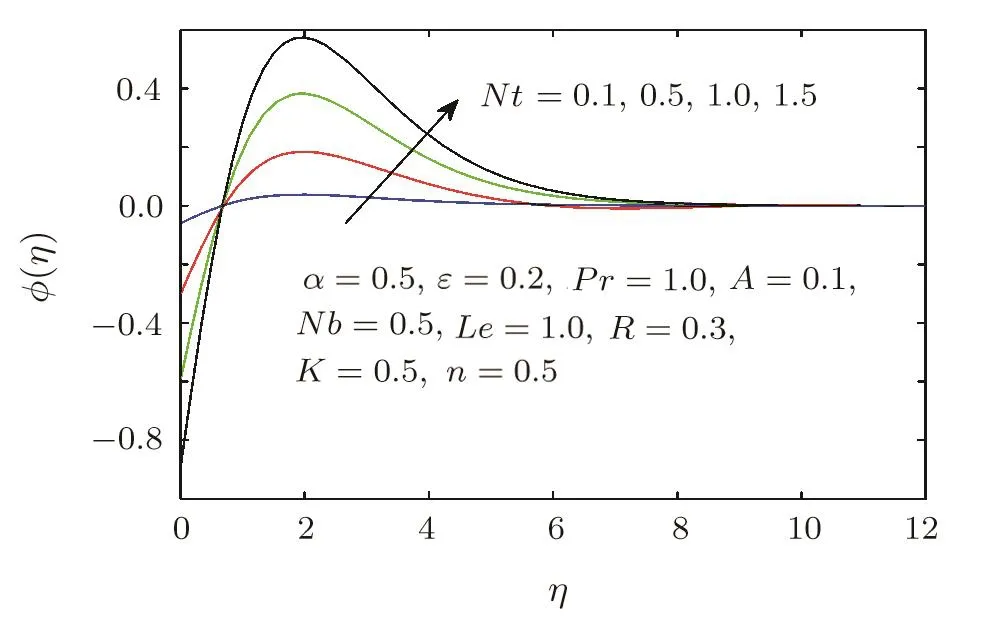
Fig.24 Concentration profile ϕ(η)for different values of thermophoresis parameter Nt.

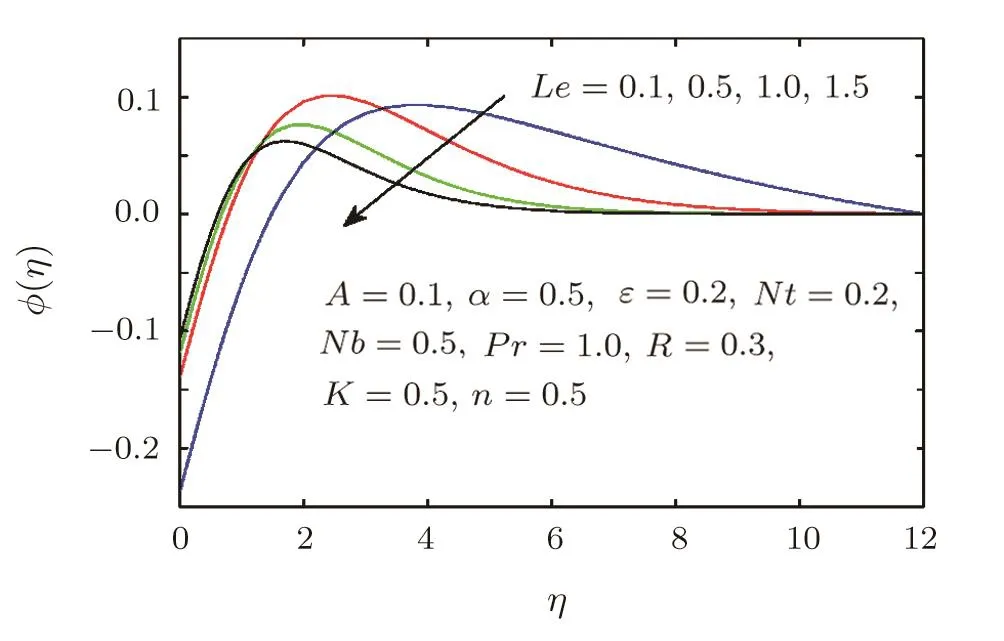
Fig.25 Concentration profile ϕ(η)for different values of Lewis number Le.

5 Conclusion

The steady three-dimensional flow of Sisko fluid past a porous medium is investigated numerically.The main results of the current work are listed below,

(i)Increase in the Sisko fluid A tends to the increment in the velocity profiles f′(η)and g′(η)and reduction in the temperature and concentration distributions.

(ii)Higher values of the ratio parameter α increases the magnitude of the velocity f′(η),g′(η)and decreases the temperature and concentration profiles.

(iii)The temperature and concentration distributions are increased for the higher thermal conductivity ϵ,radiation R and it is decreased for the larger values of Prandtl number Pr.

(vi)Increment in the porous medium K creates the reduction in the velocity and rise in the temperature and concentration.

(v)Concentration profile is reduced for the increasing values of the Brownian motion Nb and Lewis number Le respectively.

(vi)Large values of the thermophoresis parameter Nt tends to the enhancement in concentration field.