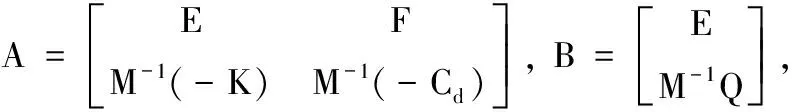基于分布式襟翼风力机桨叶的模型预测振动控制

穆安乐， 张广兴， 李迺璐， 邹阿配， 万强强， 许建国

(1. 西安理工大学 机械与精密仪器工程学院，西安 710048； 2. 扬州大学 水利与能源动力工程学院，江苏 扬州 225127)

风力发电机组呈由陆地向海上的发展趋势[1]。海上风力机为充分捕获风能，额定功率要求增大，桨叶尺寸随之变大。例如，直径高达160 m的大型风力机已投入试运行[2]。由于大展弦比的桨叶柔性高，在以往直径较小的风机桨叶研究中气动弹性效应没有受到重视[3]。在实际风场中，整个风轮上的风速并不均匀。造成风桨叶载荷不平衡，易引起桨叶振动。又因传统主动变桨距控制需要桨叶整体变动，不能应对局部不均载荷；且桨叶惯性大、反应滞后，不能应对突发阵风和极限风速下高频振荡载荷等问题，需要研究针对局部桨叶的有效减振降载控制技术。

近年来，国内外科研人员对风力机桨叶振动及振动控制技术做了很多研究。以图1所示加装尾缘襟翼为代表的“智能桨叶”通过局部气动控制技术，利用桨叶气动弹性效应，改变桨叶展长指定位置的气动特性，可以实现精准的振动控制，使得“智能桨叶”技术脱颖而出。

图1 分布式襟翼智能桨叶概念图Fig.1 Schematic of smart blade concept with distributed flaps

例如，Andersen等[4]设计了PD调节器，计算证明尾缘襟翼减小桨叶疲劳载荷的潜力。Van Wingerden等[5-6]通过实验验证了“智能桨叶”概念减少载荷的可行性；又于2011年设计H∞控制器，实验表明气动载荷波动最多可减少90%。 Ng等用线性非定常涡格法计算气动力建立风力机桨叶气动弹性模型，采用H∞调节器，计算结果说明尾缘襟翼能够降低整机13%载荷。Leonardo等[7]提出采用尾缘襟翼的智能转子来对桨叶主动降载，通过线性二次型控制算法，仿真表明降低桨叶根部弯曲力矩降低10%。郝礼书等[8]对加装Gurney襟翼的风力机桨叶翼型气动载荷控制进行了数值模拟研究，着重讨论了Gurney襟翼对翼型气动载荷的影响。莫文威等[9]利用多体动力学对风力机桨叶进行气弹耦合及稳定性分析。李迺璐等[10]对风力机桨叶在非定常气动力下的颤振稳定性进行了分析。李德源等[11]利用超级单元的方法，对柔性桨叶的气弹耦合进行了研究，为整机的气弹耦合及稳定性分析提供了分析方法。张明明等[12-13]研发了安装有柔性尾缘襟翼的“智能桨叶”的整体风力机气动伺服弹性仿真平台，与传统整体变桨相比，由于智能控制改变了桨叶上的气动特性，大大增加了流-固系统的阻尼，因此能够有效降低在桨叶和传动链上的载荷，表明了“智能桨叶”对减轻疲劳载荷的有效性。刘廷瑞等[14]针对桨叶的失速非线性颤振问题，讨论了气弹智能控制的数值模拟过程。

从上述报道可知，尽管近年来国内外对大型风力机气弹耦合及稳定稳定性已经做了很好的研究，但对大展弦比风力机桨叶气动弹性理论建模的停留在二维翼型截面，国内应用主动控制的“智能桨叶”研究鲜有报道；并且在“智能桨叶”结构主动控制技术相结合这方面研究依然研究不足。因此，本文将大展弦比风力机桨叶简化为复合材料悬臂梁叠层板，然后通过Rayleigh-Ritz法和Theodorsen片条理论得出了基于尾缘襟翼的桨叶三维气弹耦合模型。

模型预测控制(Model Predictive Control，MPC)是20世纪80年代初开始发展起来的一类新型计算机控制算法[15]，并且受到了工业界和学术界研究人员的持续关注。它具有控制效果好、鲁棒性强、对模型精确性要求不高等优点，同时它可处理输入输出有约束、多目标优化跟踪等复杂问题。因此本文在最后通过模型预测控制算法对分布式尾缘襟翼对系统进行主动控制，实现了尾缘襟翼对大展弦比桨叶减振降载的目的。

1 带分布式尾缘襟翼的桨叶数学模型

1.1 桨叶气动弹性模型

这里以均质、对称的悬臂梁模型作为风力机研究对象，简化模型如图2。

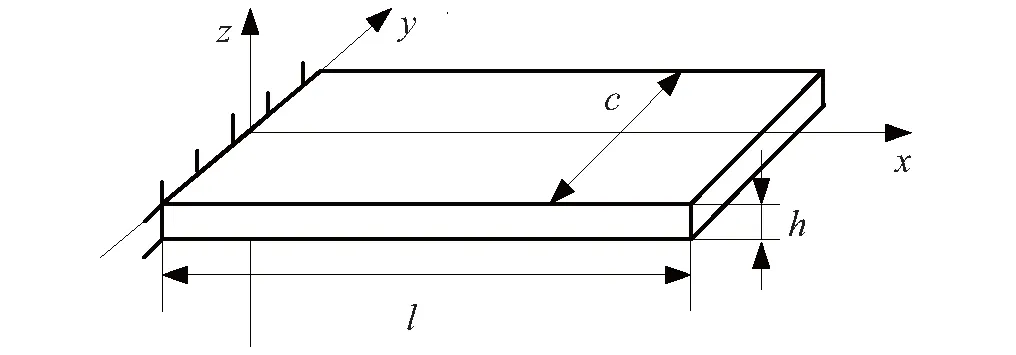
图2 桨叶的简化悬臂梁模型Fig.2 Simplified cantilever beam model of blade

根据Rayleigh-Ritz法[16]桨叶的纵向变形位移ω可写成如下形式

(1)

式中：φi(x)和ψi(y)分别为桨叶沿x和y坐标方向的第i阶阵型函数；qi(t)为第i阶广义位移。

阵型函数的选取必须满足悬臂梁的边界条件。本文N值取为3，阵型函数[17]如下：

φ1(x)=悬臂梁一阶弯曲阵型，ψ1(y)=1；

φ2(x)=悬臂梁二阶弯曲阵型，ψ2(y)=1；

φ3=sin[πx/(2l)]，ψ3(y)=y/c。

式中：l为桨叶展长；c为桨叶弦长。

桨叶的动能为

(2)

式中：m为桨叶单位面积的密度。

桨叶应变势能[18]为

(3)

式中：Dij是叠层板的弯曲刚度，它是由每一层板的叠层方向和顺序决定的。

风力机的桨叶翼型横断面见图3。

可得气动力和气动力矩在桨叶上做的虚功为：

(4)

式中： ∂h, ∂α, ∂qi为虚位移；L和M分别为作用在桨叶横截面上的气动力和气动力矩；Qi为广义力。

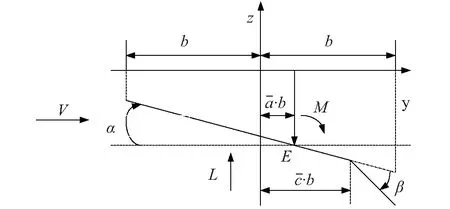
图3 翼型横断面分析图Fig.3 Airfoil cross-section of analysis model geometry

桨叶的振动位移，即桨叶横截面的挥舞与扭转弯曲位移移由式(1)可得为

(5)

式中：α为桨叶攻角；α0为桨叶根部攻角；h为桨叶挥舞位移。

桨叶截面的气动力、气动力矩和广义力可由Theodorsen片条理论[19]可得

(6)

(7)

(8)

1.2 尾缘襟翼模型

将尾缘襟翼作为控制面分布安装于风力机桨叶展长方向上，调节襟翼偏转角发生变化，对整个桨叶产生附加局部升力和力矩。分布式尾缘襟翼的气动力计算采用片条理论，设其函数为：

β(x,t)=φ4(x)q4(t)

(9)

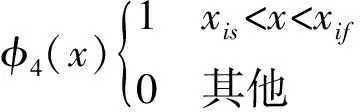
式中：xis、xif分别为第i个尾缘襟翼沿桨叶展长方向安装的始末位置。

因襟翼相对于桨叶具有质量小、高带宽的特点，故忽略襟翼的质量及变形对桨叶气动特性的影响。可得襟翼控制量为：

q4(t)=u(t)

(10)

式中：u(t)为被控襟翼所输入的偏转角。

1.3 传感器模型

由前面模态阵型可知，可以选取两个直线位移传感器和一个角位移传感器。由式(5)可得测量响应为：

式中：xtran1、ytran1、xtran2、ytran2、xang1、yang1为传感器的位置坐标。

综上，将桨叶气动弹性动力学模型、尾缘襟翼模型和传感器模型代入动能、势能和广义力公式中，由拉格朗日方程可得简化桨叶气动弹性动力学方程：

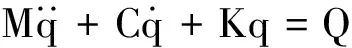
(11)

式中：M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；Q为所施加主动力，具体的表达式见附录1。

对上式进行变换，可得控制系统的状态空间模型：

(12)

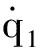
2 MPC控制系统设计

基于以上控制系统模型和研究内容，本文提出的控制目标是：在不考虑桨叶根部处的初始攻角时，设计一种控制策略，使桨叶在正常运行和突发阵风引起的气动载荷扰动的影响情况下，能有效降低挥舞位移h和扭转角位移α，以达到减振降载的目的。

为达到以上控制目标，本文使用模型预测控(MPC)算法。MPC算法由多步预测、滚动优化和反馈校正等部分构成，控制结构如图4。

图4 预测控制系统结构Fig.4 The system structure of predictive control

图4中：y(r)为输入参考轨迹；u(k)为控制输入；d(k)为扰动误差；y(k)为测量输出。

本文采用分布式尾缘襟翼控制面作为执行器；控制参数为尾缘襟翼控制面的偏转角。本文优化目标采用二次型函数：

(13)

式中： 第一项为测量输出与期望输出之间误差函数； 第二项为输入增量加权函数，λ(j)为控制加权系数。其中测量输出为桨叶的振动位移，输入量为尾缘襟翼的偏转角。

为了更加直观的看出模型预测控制算法的控制效果，传统最优控制算法也将应用到下节的仿真分析中。最优控制的性能指标取为:

(14)

式中：R为对称正定阵;Q为对称半正定阵。

3 桨叶襟翼的振动MPC仿真

本节讨论分布式尾缘襟翼控制风力机桨叶闭环系统在MPC控制下的仿真结果。模型参数见表1[15]和表2。

表1 气弹模型中叠层板材料特性

表2 翼型和气动参数

3.1 闭环仿真分析

由于桨叶弯曲和扭转之间存在耦合，故不同的控制襟翼之间存在相互影响。如何对多个分布襟翼之间的耦合进行解耦以求对单个输出的控制是非常困难的。所以本文设计了MIMO模型预测反馈控制器。

模型预测控制取采样步长为0.05，预测步长为10，控制步长为6，初始条件与开环初始条件相同，闭环仿真结果如图5所示。在有初始速度的情况下，输出位移的响应振幅快速收敛，与开环输出响应曲线相比，预测控制下的闭环反馈曲线振幅有了明显减小，其中桨叶展长方向中部振幅减小约15%，叶尖处振幅减小约30%，而扭转响应振幅减小约70%；同时回到平衡位置的响应时间也明显缩短约50%。与传统最优控制相比，预测控制下的输出振幅要小的多，并且回到平衡位置处的响应时间少。

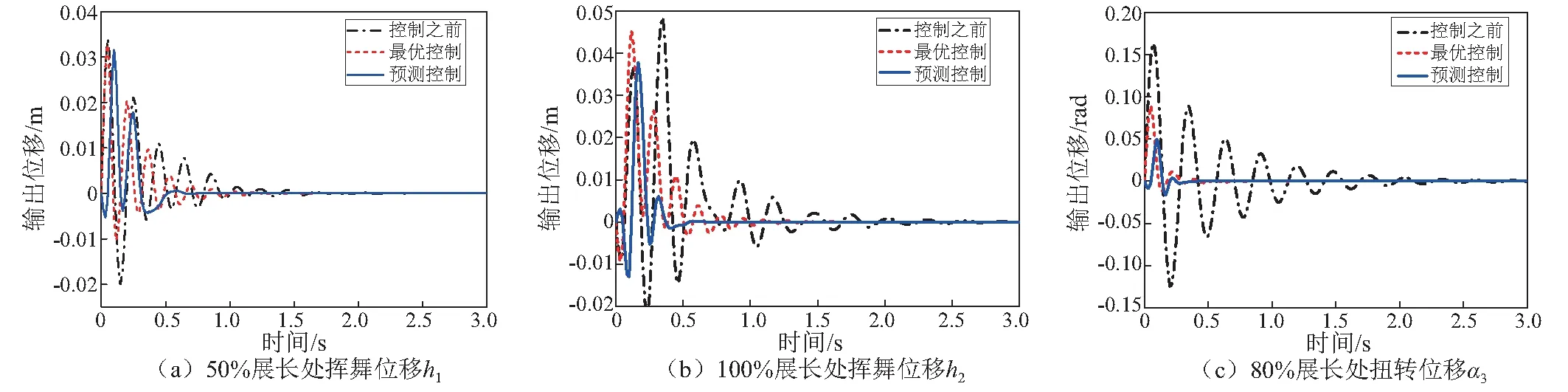
图5 开环和闭环仿真结果Fig.5 The simulation results of the closed-loop and open-loop

3.2 风速干扰闭环分析

考虑到风速和风向的变化将会引起桨叶运行带来的扰动，本文以阶跃扰动和随机扰动作为突发阵风和随机风引起桨叶攻角扰动变化的噪声信号进行仿真。取采样步长为0.05，预测步长为10，控制步长为6。图6和图7分别是在第0.75 s时加入幅值0.05、时长0.75 s的阶跃扰动和随机扰动系统闭环输出响应。图6、图7中系统输出响应在受到扰动后出现挥舞和扭转振动，在控制器的作用下振动由强变弱，幅值均得到有效抑制并快速收敛到设定稳定值。说明所设计预测控制闭环系统具有很好的鲁棒性；随机扰动比阶跃扰动所引起扭转的输出振幅大，但是也很快稳定到设定值。与传统的最优控制算法相比，预测控制对扰动引起的振动幅值的抑制作用明显优于最优控制；但是在抑制攻角振动的响应时间要比最优控制响应时间长。

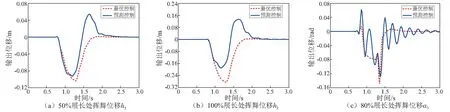
图6 阶跃扰动下的输出响应Fig.6 The outputs response under the step disturbance

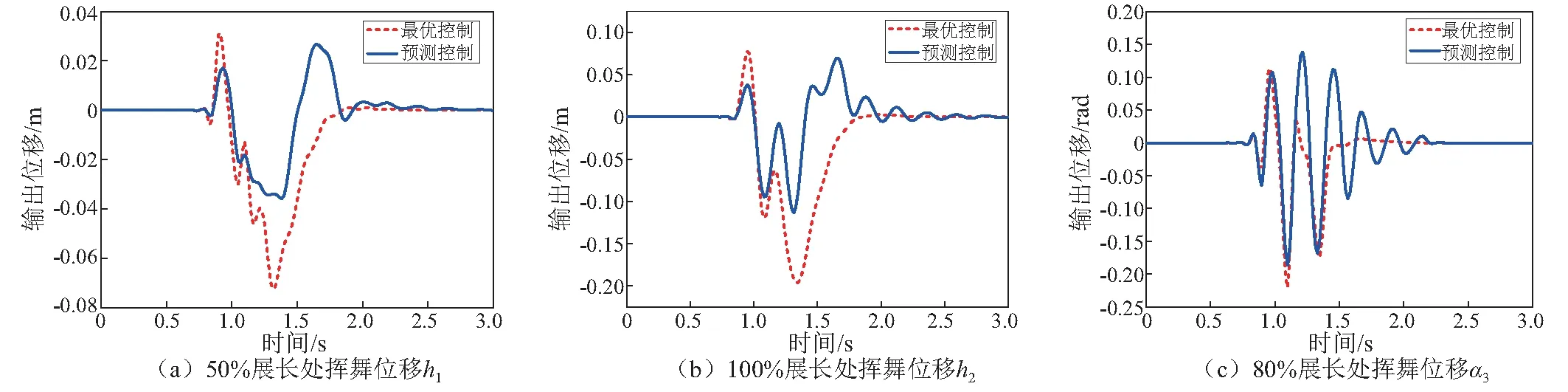
图7 随机扰动下的输出响应Fig.7 The outputs response under the random disturbance

4 结 论

本文将分布式尾缘襟翼安装于风力机桨叶上，通过对桨叶的气动弹性模型进行预测控制的仿真研究，得到以下结论：

(1) 分布式尾缘襟翼在预测控制器的调节下能有效减小桨叶挥舞和扭转振动，并且减振降载效果良好。其中展长方向上桨叶中部和叶尖处挥舞振动位移分别减小约15%、30%，扭转振动位移减小约70%；系统响应时间缩短约50%。

(2) 针对不同的阶跃和随机扰动噪声信号，MPC主动控制系统能够快速回到稳定平衡位置，具有较强的鲁棒性。

(3) 与传统最优控制相比，模型预测控制算法对抑制系统振动的幅值效果最佳；但是在控制攻角振动时其响应时间较长。综合两种控制算法仿真结果，模型预测控制在抑制振动幅值和缩短响应时间的整体性能更优。

附录：

1.

2.