隧道瓦斯爆炸数值分析与爆源类型确定研究

李志鹏， 吴顺川， 严 琼， 蒋一波

(1. 北京科技大学 土木与资源工程学院，北京 100083； 2. 中电建路桥集团有限公司，北京 100048)

近年来，社会经济高速发展，各生产领域爆炸事故频发，其中危害最大、使国民经济受到巨大损失的一类为瓦斯爆炸事故。数值模拟方法在研究爆炸冲击问题中具有显著地高效性[1]，随着力学、数学尤其是计算机技术的快速发展，数值计算的精准度也在不断提高[2]。在瓦斯爆炸问题研究中首先需确定爆炸荷载——即数值模型中的爆源。

方秦等[3]将“天津港8.12特大爆炸”事故中危化品等效为一定当量的TNT评估爆炸威力；耿振刚等[4]采用等效TNT当量法研究了温压炸药在坑道内的爆炸特性；姚术健等[5]采用等效TNT当量法研究了汽车炸弹爆炸作用下桥梁的破坏效应；马砺等[6]、文霞等[7]均采用等效TNT当量法分别研究了储油罐、输气管道泄漏引发爆炸所产生的冲击效应；张秀华等[8-9]将可燃气体直接作为爆源模拟了乙炔-空气爆炸作用下爆炸冲击波特征、以甲烷-空气作为爆源模拟室内燃气爆炸作用下钢结构动力响应及对TNT、乙炔-空气在自由空间爆炸作用下的冲击波强度特征进行比较。以上学者的研究对数值模拟中爆源选取具有积极的指导作用，大致总结为两类：等效TNT当量法与可燃气体法。

本文通过介绍数值计算中爆源的两种模拟方法，分析了以TNT、可燃气体为爆源分别在自由空间与半自由空间内爆炸作用下爆炸冲击波的特征及约束结构的动力响应，并以成都洛带古镇隧道瓦斯爆炸致灾为工程背景建立流固耦合数值模型，修正RHT模型参数以模拟衬砌结构的动态响应，通过计算得到隧道内积聚瓦斯的等效TNT当量，分别计算分析了以TNT、可燃气体为爆源的爆炸作用下隧道衬砌结构的损伤特征并与实际损伤调查相对比，初步探索了采用数值模拟在隧道瓦斯爆炸研究中的爆源确定问题，研究可指导洛带古镇隧道爆炸致灾后衬砌结构安全评价、修复加固工作及为类似地下工程瓦斯爆炸研究提供参考。

1 爆源确定方法

1.1 等效TNT当量法

等效TNT当量法，即采用高能炸药TNT作为中间媒介，根据能量相似原理以瓦斯与TNT的爆热比关系换算得到定量瓦斯的等效TNT当量，如式(1)～(2)所示，瓦斯是多种气体的混合物，主要可燃物为甲烷(CH4)。

(1)

MTNT=αEQVGρG

(2)

式中：QG为甲烷爆热， MJ/kg；QT为TNT爆热，一般取4.5 MJ/kg；Eq为单位质量甲烷与TNT的爆热比；α为瓦斯中甲烷含量；VG为瓦斯体积，m3；ρG为甲烷密度，取0.716 kg/m3；MTNT为隧道内积聚瓦斯的等效TNT当量。

由甲烷燃烧方程式(3)知，单位质量甲烷完全燃烧放热量为55.64 MJ/kg[10]。

CH4+2O2⟹CO2+2H2O+890.3 kJ

(3)

当瓦斯完全燃烧时甲烷的浓度可由式(4)计算得9.5%[10]：

(4)

式中：n0为1 mol可燃气体燃烧时所需要的氧摩尔数，取2。

当瓦斯中甲烷含量达9.5%时，甲烷和氧气完全反应，瓦斯爆炸威力最大，故式(2)中α为9.5%，为55.64 MJ/kg。

1.2 可燃气体法

该方法假设瓦斯-空气混合气体真实存在，爆炸前混合气体处于常温、常压均匀状态，比热容随温度变化，满足理想气体的状态方程，爆炸过程为单向不可逆反应，基于质量、动量及能量守恒原理求解爆轰波的Hugoniot与Rayleigh方程得到得混合气体爆炸参数[11]，式(5)～(6)所示。

(5)

(6)

式中：e0、ej分别为爆炸前、后的爆炸物内能；p0、pj分别为爆炸前、后的压力；V0、Vj分别为爆炸前、后气体的比容；Qe表示爆热；D表示爆速。

2 不同爆源的爆炸特征研究

采用显式动力学分析软件LS-DYNA建立流固耦合数值模型，对TNT、可燃气体(瓦斯-空气)两种爆源分别在自由空间与半自由空间(X-Y方向受混凝土结构约束，厚12 cm，Z方向自由)爆炸作用下爆炸冲击波传播特征与结构动力响应进行分析并验证模型。

2.1 数值模型

由式(1)换算得：100 kg(0.061 m3)TNT爆炸等效为162.93 kg(132.03 m3)的瓦斯-空气混合气体爆炸，建立表1中不同工况的爆源-空气、爆源-混凝土结构-空气流固耦合数值模型，爆源几何结构为球体。

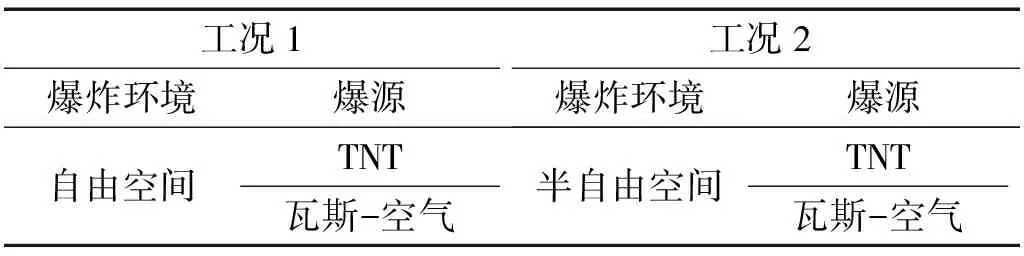
表1 数值模拟工况

工况1、2均选取1/8模型计算，起爆位置位于坐标原点处，除对称边界外其余均设置为无反射边界，数值模型如图1、2所示。

图1 工况1数值模型Fig.1 Numerical model of 1st situation

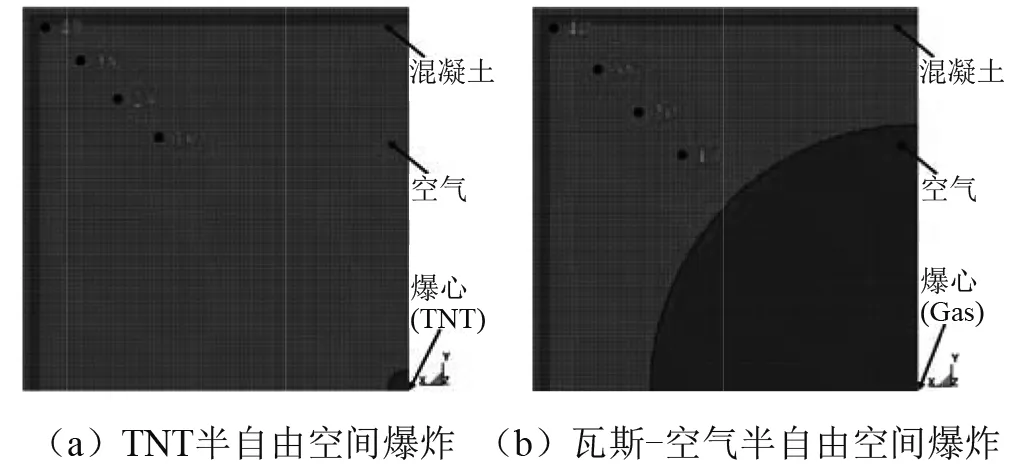
图2 工况2数值模型Fig.2 Numerical model of 2nd situation

2.2 计算参数

2.2.1 TNT

LS-DYNA中TNT的本构模型与状态方程分别为*MAT_HIGH_EXPLOSIVE_BURN与*EOS_JWL[12]，计算参数如表2所示。

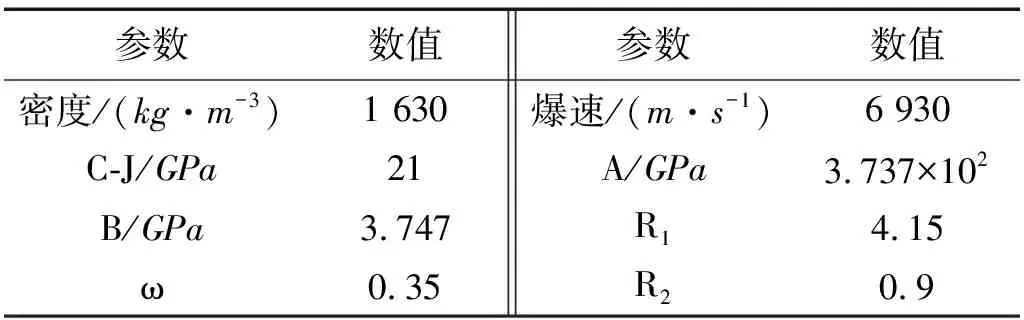
表2 TNT计算参数

2.2.2 可燃气体

可燃气体为瓦斯-空气混合气体，其本构模型采用LS-DYNA中的*MAT_NULL，状态方程为*EOS_LINEAR_POLYMNOMIAL[12]，计算参数如表3所示。

表3 可燃气体计算参数

2.2.3 空 气

空气的本构模型与状态方程与可燃气体相同，计算参数如表4所示。

表4 空气计算参数

2.2.4 混凝土

混凝土结构采用LS-DYNA中RHT模型[13]，该模型能较好模拟混凝土材料在爆炸冲击荷载作用下的动力特性[14]，计算参数如表5所示[15]。

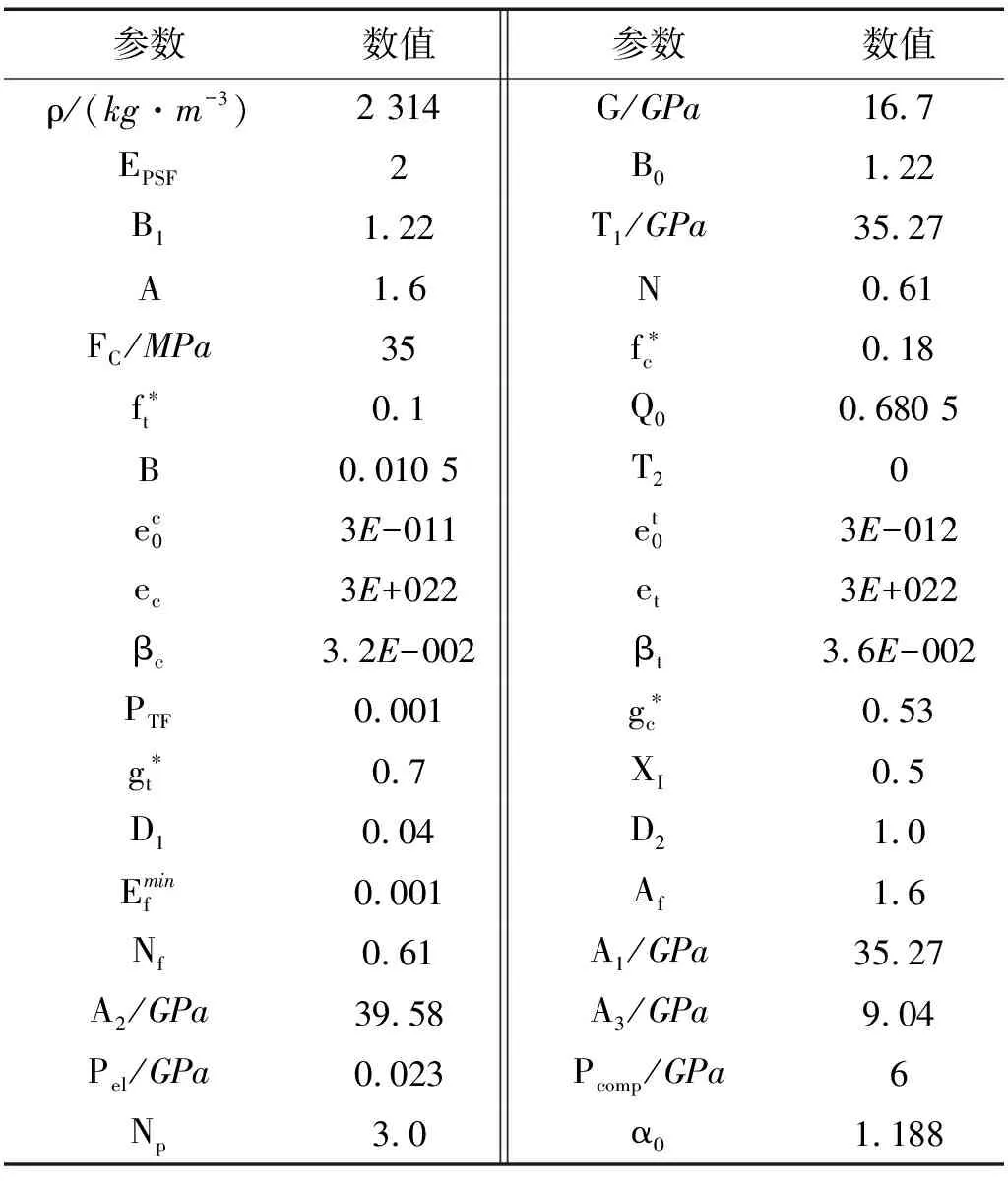
表5 混凝土计算参数

2.3 数值模拟结果与验证

2.3.1 爆炸冲击波传播特征

在图1、2所示的数值模型均布设4个等间距测点，就各测点的超压时程曲线及超压峰值进行分析，探究TNT、瓦斯-空气两种爆源分别在自由、半自由空间爆炸作用下爆炸冲击波的传播特征。

由图3、4可知：

(1) TNT在自由空间爆炸作用下，如图3(a)所示，测点处压强依次达到最大超压峰值后迅速衰减至爆炸前状态，随测点爆心距增大，各测点最大超压峰值呈衰减趋势，属于典型的点源爆炸。

瓦斯-空气在自由空间爆炸作用下，如图3(b)所示，测点处压强达到最大超压峰值后衰减缓慢并出现波动峰值，各测点的最大超压峰值相差不大，可能原因为：混合气体燃烧爆炸非点源爆炸，相比于TNT，爆速较低，爆炸冲击波逐层依次向外传播。距爆心由近及远的1#～4#测点超压峰值在层层冲击波作用下超压峰值持续作用时间逐渐变短，后续的脉动波峰为混合气体的爆炸产物继续膨胀做功所产生。

(2) TNT在半自由空间爆炸作用下，如图4(a)所示，最大超压峰值测点为距离混凝土结构最近的4#测点(11.2 MPa)，这是由于爆炸冲击波在混凝土表面发生反射且4#测点处为“犄角结构”致使该处超压峰值剧增且作用时间较长。图中A点表示3#测点处压强在初始爆炸冲击波作用下达到一个超压峰值(0.68 MPa)，B点受冲击波反射影响形成的超压峰值(1.46 MPa)，而远离混凝土结构的1#～2#测点并未受到显著影响，表明爆炸冲击波在结构处(障碍物)发生反射后使结构附近区域压强剧增。

图3 工况1下各测点的超压时程曲线及超压峰值Fig.3 Overpressures time-history curves and Max. pressure of 1st situation surveying points

瓦斯-空气在半自由空间爆炸作用下，各测点的爆心距均较小故超压峰值都得到不同程度增加，如图4(b)所示，与TNT爆炸相似最大超压峰值位于靠近混凝土结构的4#测点，达3.36 MPa。

2.3.2 结构动力响应与损伤

通过对图5中混凝土结构上测点(1#～3#)的超压-时程曲线及测点在X方向上的加速度-时程曲线、速度-时程曲线及位移-时程曲线分析，如图6、图7所示，探究在TNT、瓦斯-空气两种爆源在半自由空间爆炸作用下结构的动力响应特征。

图4 工况2下各测点的超压时程曲线及超压峰值Fig.4 Overpressures time-history curves and Max. pressure of 2nd situation surveying points

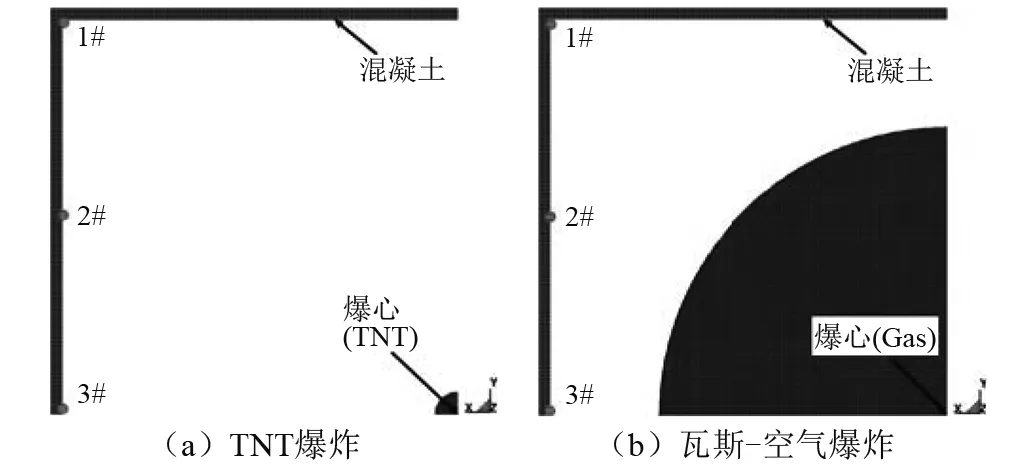
图5 混凝土结构测点分布Fig.5 Measuring points arrangement on concrete structure

图6 TNT爆炸作用下混凝土结构的动力响应Fig.6 Dynamic responses of concrete structure under TNT explosion

TNT爆炸作用下，如图6所示，3#测点爆心距最小且主要受X方向的爆炸冲击荷载，速度与位移峰值均最大，分别为25.5 m/s、10.1 cm；超压峰值较2#测点大，为5.95 MPa；加速度峰值接近与2#测点，达2 120 g。由测点速度-时程曲线后期增长趋势变缓及加速度-时程曲线后期振幅减小可知，冲击荷载衰减较快，结构受强烈冲击但作用时间较短。

如图7(b)、图7(c)所示，在瓦斯-空气爆炸作用下，测点加速度、速度时程曲线波动较大且衰减缓慢，结构受爆炸荷载作用时间较长；1#～3#测点到爆源距离相差甚微，“犄角结构”处爆炸冲击波增强效应显著，故1#测点超压峰值最大，达3.36 MPa。

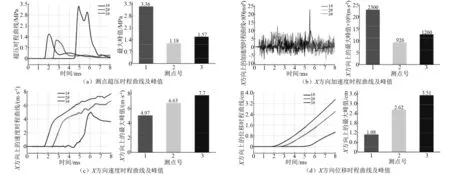
图7 瓦斯-空气爆炸作用下混凝土结构的动力响应Fig.7 Dynamic responses of concrete structure under gas explosion

对比图6、7可知：

(1) TNT、瓦斯-空气爆炸作用下结构的动力响应特征有所不同：在TNT爆炸作用下，结构受到的爆炸冲击荷载很大，但荷载作用时间极为短暂，几乎瞬间完成且冲击荷载随爆心距增加衰减很快；在瓦斯-空气爆炸作用下，结构受到爆炸冲击荷载虽小但作用时间较长且衰减较缓慢。

(2) 两种等效爆源在同一的爆炸空间内：TNT爆炸作用下，结构整体承受的爆炸冲击荷载并不均匀，主要与结构不同部位的爆心距及结构本身几何特征相关；瓦斯-空气爆炸作用下，结构整体承受的爆炸冲击荷载较为均匀，主要受结构几何特征影响。

图8中，“损伤程度=1.0”表示结构完全破坏，“损伤程度=0”表示未发生破坏。

由图8知，两种爆源爆炸作用下混凝土结构的“犄角结构”处、正对爆源的X、Y方向处损伤严重，与前文对结构动力响应分析相对应。

图8 两种爆源爆炸作用下混凝土结构的损伤Fig.8 Damage of concrete structure under the explosion of two burst source

2.3.3 数值模型验证

将TNT在自由空间爆炸下的数值计算值(如图3(a)所示)与Henrych等[16]基于大量实验提出的空中爆炸冲击波经验公式预测值进行对比，如图9所示，误差分析如表6所示。

由图表可知：数值模拟结果与经验公式较为相似，测点超压峰值变化趋势一致，计算最大误差为9.8%，最小误差为8.3%。误差分析原因主要与数值模型中的单元尺寸有关，若进一步精细模型网格，表6所示误差整体仍可减小，即便如此计算结果仍与文献[17]的研究结果基本一致，满足计算要求。综上所述，本文的研究方法与建立的数值模型可靠性强，可用于洛带古镇隧道爆炸计算分析研究。

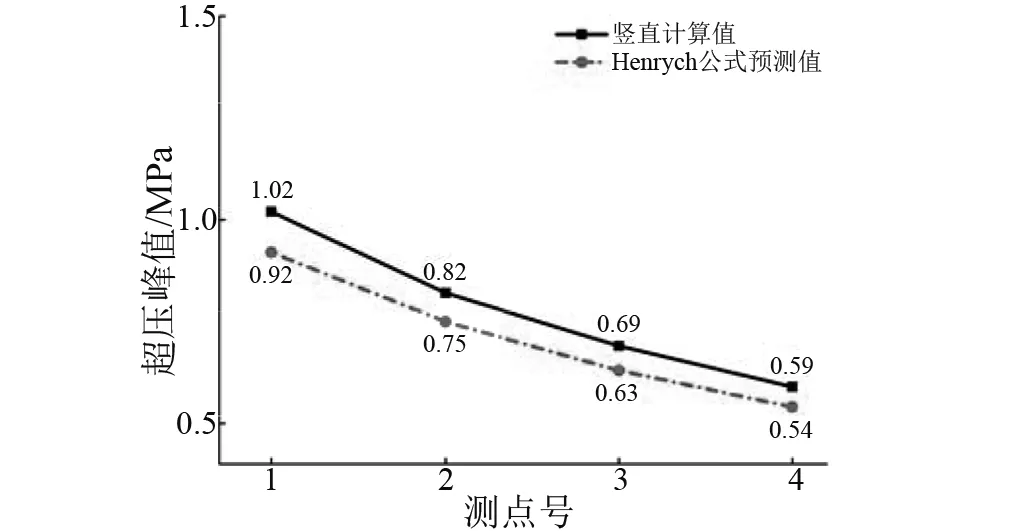
图9 TNT自由场爆炸下测点超压峰值对比Fig.9 Comparison of Max.pressure of measuring points in free-field air explosion

测点号数值计算值/MPaHenrych预测值/MPa相对误差/%11.020.9210.920.820.759.330.690.639.540.590.549.3

3 工程应用

3.1 工程背景

洛带古镇隧道瓦斯爆炸事故为近年来国内外唯一的、典型的公路隧道内剧烈爆炸案例。隧道位于四川省成都市自西向东横穿龙泉山脉，在隧道进口段现场检测瓦斯最大溢出量为0.52 m3/min，为高瓦斯隧道[18]。2015年2月24日，隧道进口段发生瓦斯爆炸，现场情况如图10(a)所示，从图中可知瓦斯爆炸威力巨大，隧道受损情况十分严重。事故调查结果显示左洞1个爆点(ZK2+810)，右洞2个爆点(K2+300、K2+587)，如图10(b)、图10(c)所示。本文选取洛带古镇隧道左洞爆炸受损部分区域(ZK2+800～ZK2+820)进行研究，该区段二衬结构为厚40 cm的C25素混凝土结构。

图10 隧道爆点示意图Fig.10 Location of explosive points in tunnels

3.2 爆 源

隧道施工期间ZK2+800～ZK2+820段检测的瓦斯溢出量为1.08 m3/min，隧道断面面积为72.34 m2，爆炸事故发生时隧道已10天未通风，由此知研究区域内已经充填满瓦斯空气混合气体，体积为1 446.8 m3，由式(1)～(2)计算得为1 216.8 kg。

3.3 数值模型及衬砌、围岩计算参数

根据该区段隧道标准横断面设计图，如图11(a)所示，构建“爆源-空气-衬砌结构-围岩”的流固耦合数值模型，爆心设置在隧道中心，爆源分别为TNT、瓦斯-空气，起爆位置距离隧道拱顶与仰拱底板等距，均为3.6 m，数值模型如图11(b)、图11(c)所示，数值模型尺寸为20.00 m×17.64 m×15.70 m(长×宽×高)，如图11(d)所示，边界条件设置为无反射边界。

图11 数值模型Fig.11 Numerical model

(1) 衬砌结构参数修正

衬砌结构采用RHT模型，对部分参数进行修正：

①为避免计算过程中衬砌结构因变形过大，导致单元网格扭曲、畸变影响计算，取最小失效拉应变为0.000 8，损伤参数D1、D1分别为0.015与1.0[19]。

②混凝土结构的压缩应变率βc和拉伸应变率βt由式(7)～(8)分别取0.042、0.044[15]。

βc=4/(20+3fc)

(7)

βt=2/(20+fc)

(8)

③初衬结构中的钢拱架与钢筋网片有效地提高了混凝土的抗拉强度，但这些钢结构密布于初衬结构，若对其建模计算将导致数值模型过于繁琐计算效率大大降低，当前多数学者将钢拱架和钢筋网片的增强作用通过等效强度原理弥散到混凝土中[20-21]，故文章也采用等效强度法由式(9)计算得初衬结构的等效抗拉强度为6.1 MPa[18]。

(9)

式中：ft为混凝土的抗拉强度，2.5 MPa；fy为钢筋的屈服强度取300 MPa；ρ为混凝土结构中含钢率，计算取1.2%。

(2) 围岩模型及参数

隧道内发生爆炸，围岩应变率效应明显，采用LS-DYNA中*MAT_PLASTIC_KINEMATIC模型，围岩屈服与加载应变率关系如式(10)～(11)，计算参数如表6所示。

(10)

Ep=EtanE0/(E0-Etan)

(11)

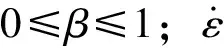
表7 围岩计算参数

3.4 不同爆源爆炸作用下隧道衬砌结构损伤特征

洛带古镇隧道分别在等效TNT当量、瓦斯-空气两种爆源爆炸作用下衬砌结构的损伤特征，如图12、13所示为，均取1/2模型进行说明。

隧道衬砌结构在等效TNT当量爆炸作用下的损伤特征如图12所示：衬砌结构迎爆面损伤程度较背爆面严重；爆心附近区域破坏严重，在拱顶附近的拱部存在大范围损伤域，隧道底板上形成面积约12.31 m2的爆坑，这是因为爆心处衬砌结构受剧烈爆炸冲击荷载的冲压、拉伸作用所致；远离爆心的衬砌结构在拱部、曲边墙部位以纵向裂缝为主局部有环向裂缝，这是由于TNT爆炸产生的冲击荷载在传播过程中衰减极快，远离爆心的衬砌结构在入射、衍射、反射冲击波的拉伸作用下产生以纵向为主的损伤裂缝；衬砌结构的曲边墙脚位置已完全破坏，该处的“犄角结构”使得冲击荷载剧增，损伤裂缝迅速发展直至贯通。

图12 TNT爆炸作用下衬砌结构的损伤特征Fig.12 Damage characteristics of lining structure under TNT explosion

图13 瓦斯-空气爆炸作用下衬砌结构的损伤状况Fig.13 Damage characteristics of lining structure under gas explosion

隧道衬砌结构在瓦斯-空气爆炸作用下的损伤特征如图13所示：衬砌结构的迎爆面与背爆面、近爆区与远离爆心区域的损伤程度相似；位于衬砌结构拱部、曲边墙上遍布纵向、环向裂缝，以错综复杂的纵向裂缝为主，这是因为瓦斯-空气燃烧爆炸产生的冲击荷载衰减缓慢、荷载峰值持续时间较长，冲击波经反射对衬砌结构产生拉伸作用致衬砌结构上损伤裂缝遍布；与TNT爆炸相似，曲边墙脚处衬砌结构已完全破坏。

图12、13与图14对比可知：爆源为等效TNT时，爆炸作用下近爆区衬砌结构损伤严重，远离爆心区损伤较轻，而数值计算范围有限故距离爆心更远区域的衬砌结构损伤计算结果将与实际情况不相符；当爆源为瓦斯-空气时，洛带古镇隧道衬砌结构整体损伤特征的数值模拟结果与实际调查情况基本一致，表明在数值计算中以瓦斯-空气模拟爆源可以较为真实反映隧道衬砌结构在瓦斯爆炸作用下的损伤特征。

图14 隧道衬砌结构实际损伤调查情况Fig.14 Investigation on actual damage of tunnel lining structures

4 结 论

本文采用数值模拟法对瓦斯爆炸问题中爆源的选取进行研究，建立流固耦合数值模型，分别对等效TNT当量、瓦斯-空气两种爆源在自由空间与半自由空间爆炸作用下爆炸冲击波的传播特征及结构的动力响应进行研究分析，并以洛带古镇隧道瓦斯爆炸事故为工程背景，对两种爆源爆炸作用下隧道衬砌结构的损伤特征进行分析并与实际损伤调查情况对比，有如下发现：

(1) TNT在自由空间爆炸作用下沿传播方向爆炸冲击波能量衰减迅速；相比较，可燃气体爆炸作用下冲击能量较小但作用时间长且缓慢衰减。

(2) 在半自由空间内，两种爆源爆炸作用下靠近结构处压强均受爆炸冲击波反射增强效应而剧增。

(3) 在TNT爆炸作用下，混凝土结构受剧烈但短暂的冲击作用；在可燃气体爆炸作用下，爆炸冲击荷载对混凝土结构作用时间较长。

(4) 洛带古镇隧道衬砌结构损伤特征为：在TNT爆炸作用下，近爆区、迎爆面的衬砌结构损伤严重，远离爆心区域在衬砌结构拱部、曲边墙上以纵向裂缝为主；在可燃气体爆炸作用下，隧道衬砌结构损伤较均匀，衬砌结构拱部、曲边墙上遍布错综复杂的纵向、环向裂缝。经对比，可燃气体模拟爆源的数值计算结果与洛带古镇隧道衬砌结构实际损伤调查情况更为接近，表明基于流固耦合数值方法以可燃气体作为爆源研究隧道内瓦斯爆炸问题是可行的，爆源、衬砌结构等计算参数取值合理。

文章研究还存在一些问题需进一步探索：

隧道内的复杂结构及施工设备将极大增强瓦斯爆炸威力、加剧衬砌结构破坏，后续研究中需考虑。