基于非线性有限元法的冰区玻璃钢实验船碰撞性能研究

2018-08-02 02:03胡文进倪宝玉白晓龙李志鹏于昌利

振动与冲击 2018年14期

胡文进，倪宝玉，白晓龙，李志鹏，于昌利

(1. 哈尔滨工程大学船舶工程学院，哈尔滨 150001；2.哈尔滨工业大学船舶与海洋工程学院，山东威海 264209)

随着全球气候变暖的加快，地球两极冰区冰层逐渐减少，冰区海洋运输和潜在的石油、天然气等能源资源开采成为可能。在能源日渐紧缺的时代，冰区航线的开通和两极地区的开发将会给人类带来更大的利益。在我国，渤海湾、辽东湾和莱州湾已相继勘探出多个浅海大油田。但是，渤海和北黄海是我国纬度最高的海区，因受强劲而稳定的西伯利亚冷高压的侵袭，每年冬季都会产生不同程度的结冰现象，尤以渤海北部辽东湾为重，渤海湾和莱州湾次之[1]。

目前，大多数冰区船舶主要以钢船为主，研究者对于钢船的碰撞分析有较多的研究[2-4]，例如，王自力等[2]研究了LPG船舷侧结构碰撞损伤过程和多种构件的抵抗作用；江华涛等[3]以油轮为研究对象，研究了油轮首部的碰撞特性；杨飞等[4]研究了船舶低速碰撞过程，并进一步将船舶碰撞过程处理为准静态过程。然而，随着近代材料革命的发展，玻璃钢在造船中已突显出其强大的生命力和广阔的发展前景。玻璃钢是玻璃纤维增强塑料的俗称或简称[5]。船用玻璃钢由于轻质、高强，具有传统造船钢材所无法比拟的特征，故备受造船界重视，经多年的开发应用，已成为一种重要的船用材料。

玻璃钢船有着轻便的结构特点，但是其材质并非金属，其与浮冰碰撞的响应结果必然与一般钢船的碰撞结果大不相同，因此有必要研究玻璃钢船在冰载荷工况下的碰撞原理，分析碰撞方式和结果，从而找到增强玻璃钢船结构的方法[6]。因此，探究玻璃钢船体与冰体碰撞后船体结构的动态响应和损伤变形，有利于优化船体的结构形式，对于提高我国船舶在冰区航行中的结构安全性能以及保障海上作业、海上运输与海上人员安全等具有重要的理论意义和应用价值。

1 数学模型

船舶与浮冰碰撞属于非线性的动态问题，根据相关力学理论[7-8]，船-冰碰撞的一般有限元方程：

(1)

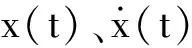
对于上面的方程，常用的有限元解法是显式积分法。

碰撞问题十分适合用中心差分法求解，具体步骤是：

(2)

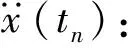
(3)

tn+1时刻的速度和位移：

(4)

本文在参考大量相关文献的基础上，在定义海冰材料属性时采用了各向同性弹塑性断裂模型，但考虑到了冰的韧脆性破坏形式。在海冰的材料模型中除需要描述弹性的应力-应变关系外，还需要有描述脆性的失效准则，选取合适的失效准则是成功构造海冰材料模型的关键。关于海冰失效准则的研究，有最大正应力准则、Von-mises准则、应变能准则和复杂的抛物线准则等[9]，但海冰物理力学性质复杂多变，这些准则都在不同程度上存在一些缺点，只有Ahmed Derradji-Aouat提出的多重失效面理论，得到了较为适合海冰数值模拟的失效准则，但该失效准则中的参数不便于工程测量，仅限于理论研究。

考虑到目前能够准确掌握的海冰材料参数，本文采用Von-mises准则作为海冰的失效准则，最大塑性应变模型作为材料的破坏模式，恒定最小压力模式作为材料的分离模式，主要参数见表1。

表1 冰的材料参数

玻璃钢属于复合材料，而复合材料是一种多相材料，由多种性质极不相同的材料组成。通过对纤维取向的设计制成的复合材料结构会出现程度不同的各向异性，复合材料性能的可设计性，是复合材料所特有的主要优点[10]。

在纤维和基体材料选定后，尚有许多材料参数和几何参数可变动，而且形成层合结构时每一层的铺设方向又可随意安排，这样就可以人为地改变组分材料的种类、含量，以及铺层方向和顺序。

铺层是层合板的基本结构单元，其厚度很薄，通常约为0.1～0.3 mm。铺层中增强纤维的方向或织物径向纤维方向为材料的主方向(1向：即纵向)；垂直于增强纤维方向或织物的纬向纤维方向为材料的另一个主方向(2向：即横向)。1-2坐标系为材料的主坐标系，又称正轴坐标系，x-y坐标系为设计参考坐标系，如图1所示。

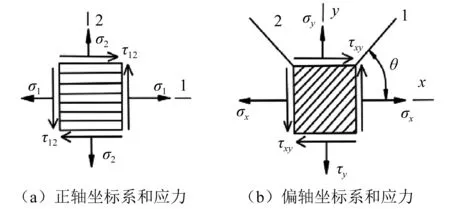
图1 铺层材料正轴与偏轴坐标系和应力Fig.1 orthoaxis and partial coordinate system and stress of layer materials

铺层是有方向性的。铺层的方向用纤维的铺向角(铺层角)θ表示。所谓铺向角(铺层角)就是铺层的纵向与层合板参考坐标x轴之间的夹角，由x轴到纤维纵向逆时针旋转为正。

纤维和基体的力学性能有很大的差异，它们组合起来构成的纤维增强复合材料在弹性常数、线膨胀系数及强度特性方面必然会表现出明显的各向异性[11]。图2表示的就是复合板铺层角度。

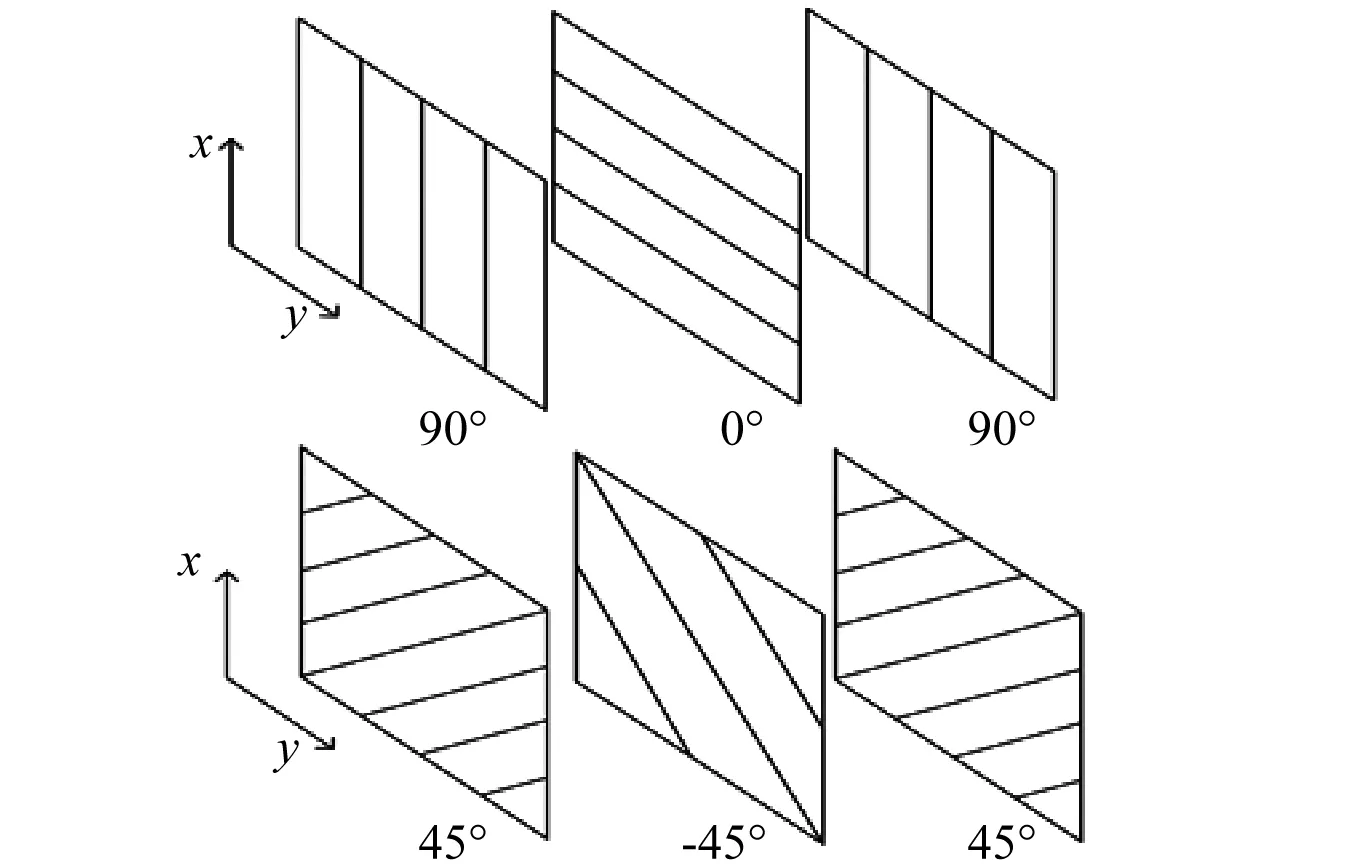
图2 玻璃纤维铺层角度示意图Fig.2 Schematic diagram of glass fiber layer

本文所采用的单元板厚为0.01 m；共5层，每层厚度0.002 m。之后设置铺层角度，本文主要研究[-45/45/-45/45/-45]和[90/0/90/0/90]这两种铺层角度碰撞后的受力情况。表2给出了玻璃钢材料的性能参数。

表2 玻璃钢的参数

2 仿真模型

鉴于本文主要考虑的是玻璃钢这种复合材料的船体的碰撞特性，故选用型线简单的小型单壳船作为船舶模型，从而突出玻璃钢的材质特性。船体的基本参数如下表3所示；图3为船模的CAD型线图，图中包括纵剖线图、横剖线图和水线图。

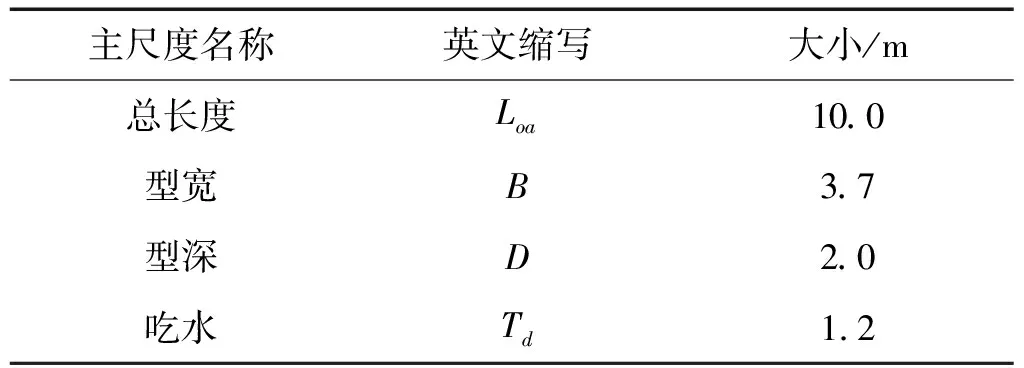
表3 船模的主要参数

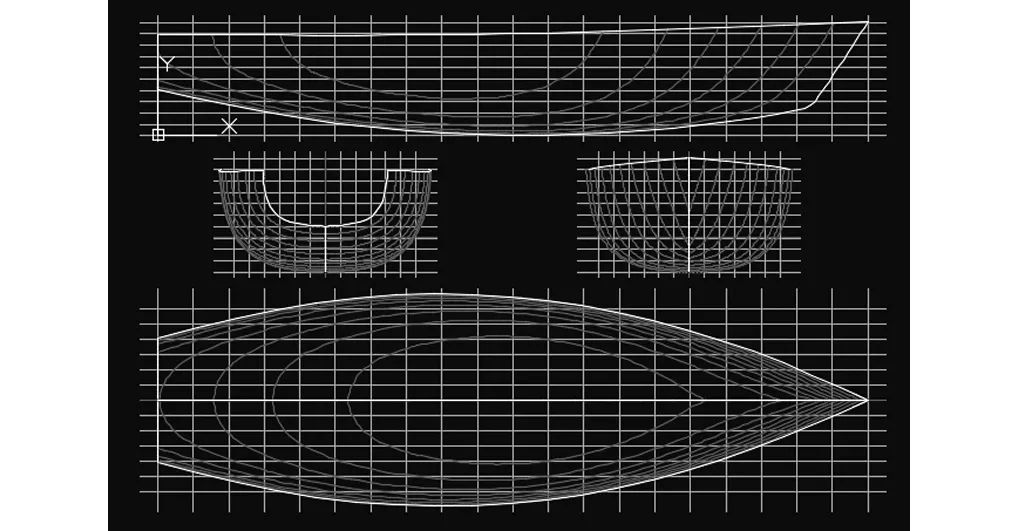
图3 船模CAD型线图Fig.3 Ship model CAD line chart

由于要研究玻璃钢铺层对碰撞的影响，必须设置SHELL163单元的特性。先设置实常数(包括单元厚度，即复合板的总厚度)。本文所采用的单元板厚为0.01 m；共5层，每层厚度0.002 m。之后设置铺层角度，分别为[-45/45/-45/45/-45]和[90/0/90/0/90]。

对于冰排，选用的单元类型为实体单元，该单元由8个节点构成，该单元只用于动力显式分析，支持所有的非线性特性，而对于SOLID164实体单元没有实常数。冰排的建模步骤较为简单，直接输入长宽高即可，基本参数如下表4。其非碰撞边界为刚性固定，碰撞边界为自由边界，即边界条件为三端刚性固定，一端自由边界。船舶为给定初始速度的六自由度自由运动。

表4 冰排模型的基本参数

3 有效性验证

在进行计算之前，有必要验证本文数值模型的有效性。为此，先计算一理想圆台状冰体与钢板的碰撞过程，提取各个时刻在被撞钢板上产生的压力，将它与现有的推荐曲线进行比较。由于计算结果输出为被撞板上的压强而非应力，故应使被撞板刚度较大[12]。

被撞板使用钢质材料，厚度为50 mm，四周刚性约束。撞击冰体距被撞板的表面距离为1 mm，以10 m/s 的速度垂直撞击被撞板，下图4即为冰体撞击钢板有限元模型。

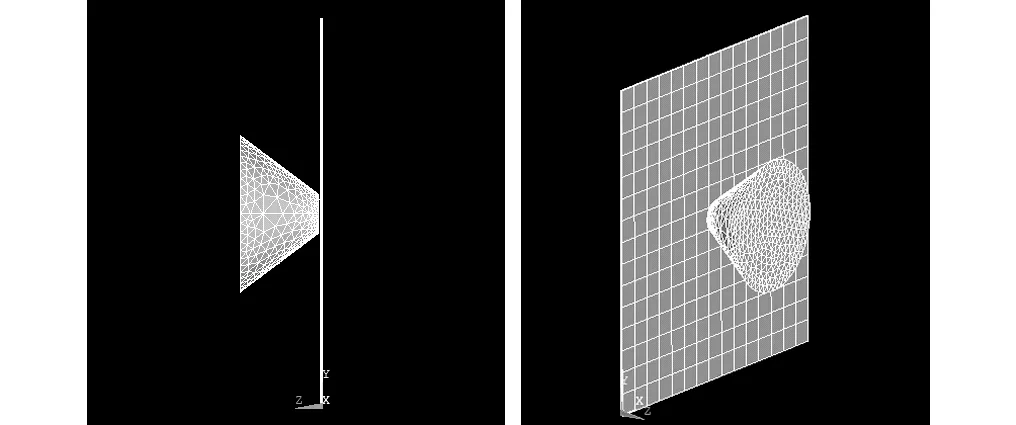
图4 冰体撞击钢板有限元模型Fig.4 Finite element model of impact between ice cone and steel plate

国际标准化委员会在ISO/CD19906—2010中推荐了冰山碰撞载荷下造成严重事故(ALIE)时冰体材料的压强面积曲线，它是一条反比例曲线:

P=7.4A-0.74

(5)

式中：P为接触面的压强；A为碰撞接触面面积。

在有限元仿真过程中，可以根据所建冰体模型在碰撞仿真过程中的压强-面积曲线与上式所得曲线进行对比，进而衡量冰体模型的准确性。二者的对比曲线如图5所示。可以看出，模拟结果与ISO推荐曲线较为一致。

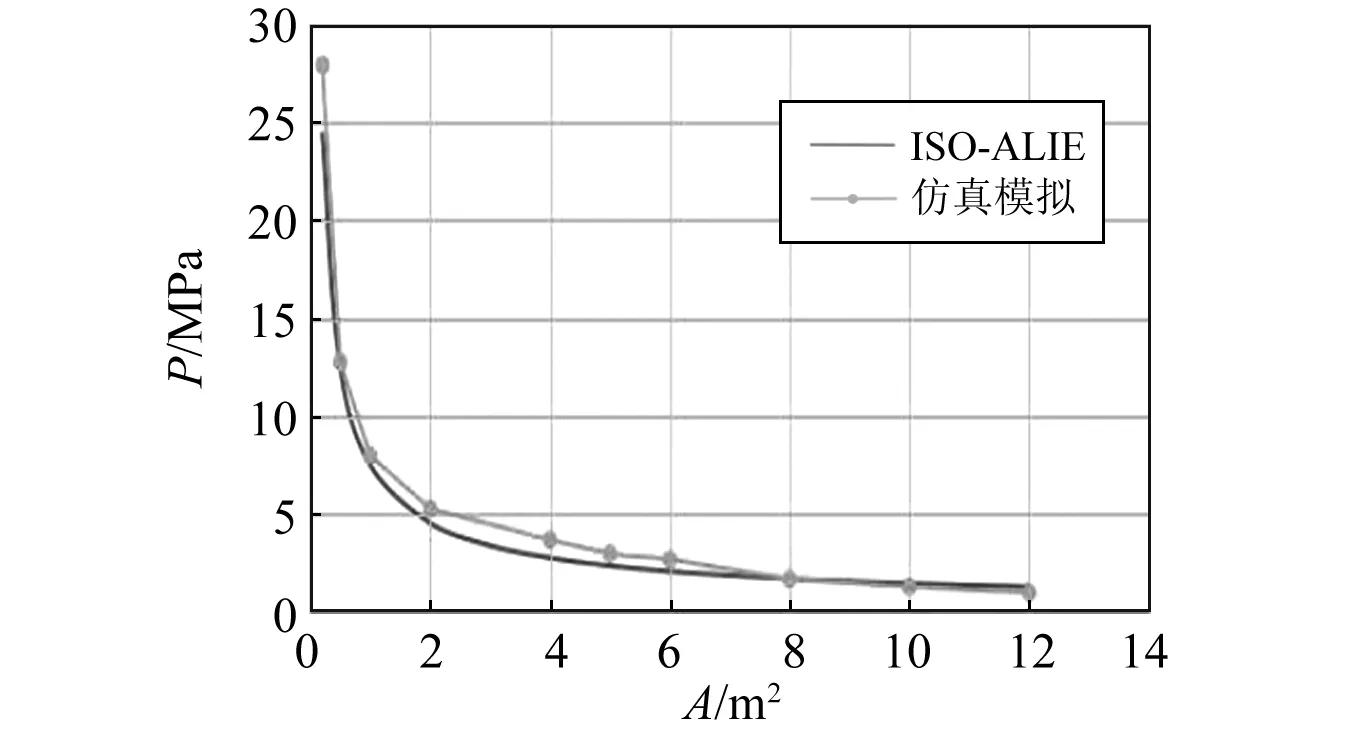
图5 模型计算结果与ISO-ALIE推荐曲线对比图Fig.5 Comparison diagram of the model calculation results ISO-ALIE recommendation curve

4 碰撞过程及结果分析

本文中的船-冰碰撞模拟中采用的碰撞方式为船艏与冰排垂直相撞，船舶与冰排的垂直距离为0.50 m，且冰排位于船舶设计水线处。定义船舶初始运动方向为x方向。船舶发生垂直碰撞的时候，由于碰撞过程结构之间的摩擦距离很短，且撞击力占主导地位，因此在实际分析时忽略摩擦对碰撞的影响[13-15]。

图6表示的是在[90/0/90/0/90]铺层下，船以6 m/s的速度与冰排碰撞前后的有限元模型应力对比云图，碰撞后截取的时刻为0.5 s。从中可见，冰排在楔形船艏的撞击作用下会产生大变形和破碎，船舶在海冰的反作用力下会产生相应的运动和应力。尽管海冰和船舶都是左右对称的，但是船-冰碰撞中海冰的破碎具有一定的随机性，会导致后期海冰裂纹的扩展和船舶运动并不是完全对称的。

(1)工况一：不同铺层方向下碰撞后的受力情况

船舶初始速度设为6 m/s。碰撞应力监测点均为船艏上与冰排最早接触的外板单元节点。图7～图16中，横坐标单位均为秒(s)。其中，对于应力曲线图，纵坐标单位均为帕(Pa)；对于船艏碰撞力曲线图，纵坐标单位均为牛顿(N)；对于船艏速度曲线图，纵坐标单位均为米每秒(m/s)；对于能量曲线图，纵坐标单位均为焦耳(J)。

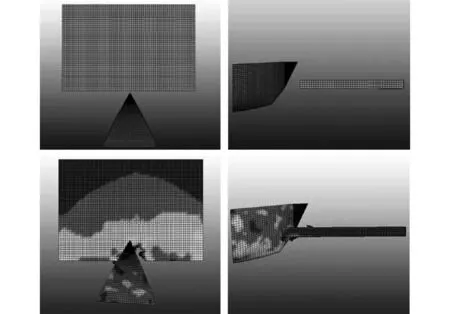
图6 船艏与冰排碰撞的有限元模型Fig.6 The finite element model of the ship and the ice floe collision

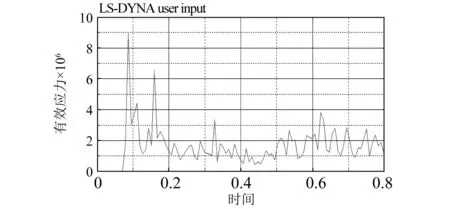
图7 [90/0/90/0/90]铺层下船艏碰撞点有效应力曲线Fig.7 Effective stress curve of ship collision point under [90/0/90/0/90] layer

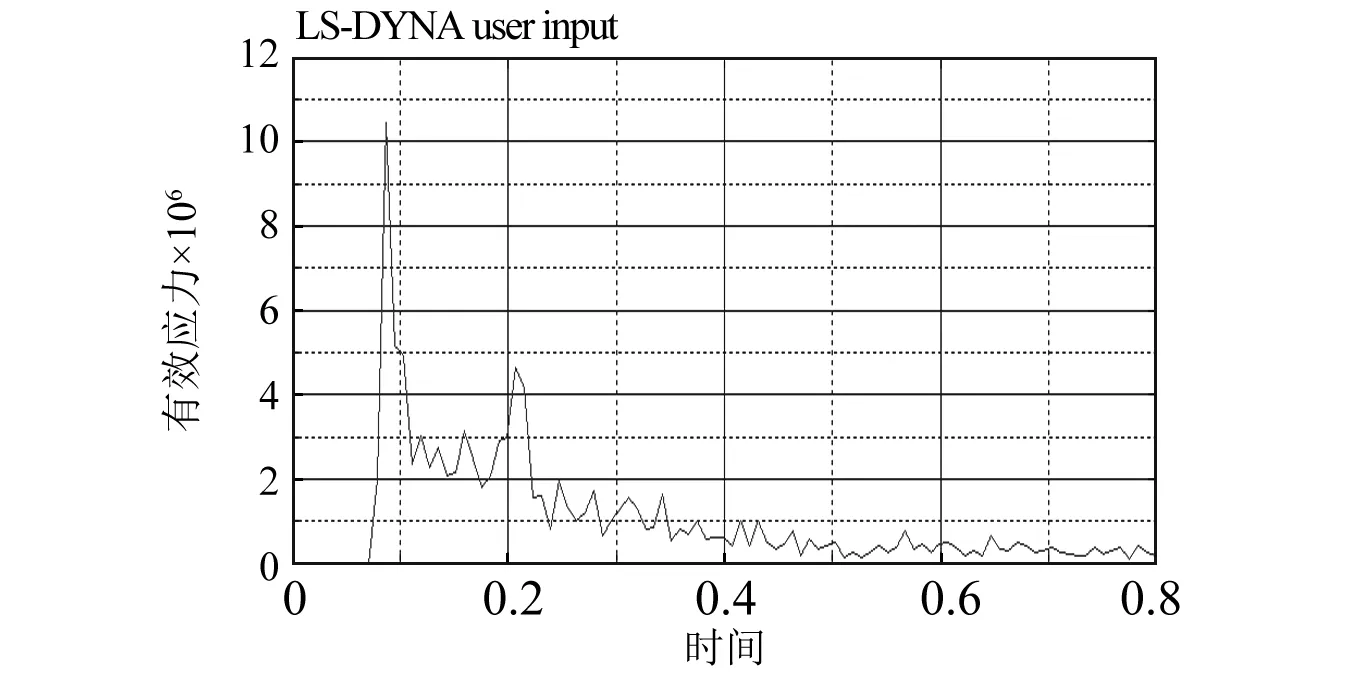
图8 [-45/45/-45/45/-45]铺层下船艏碰撞点有效应力曲线Fig.8 Effective stress curve of ship collision point under [-45/45/-45/45/-45] layer

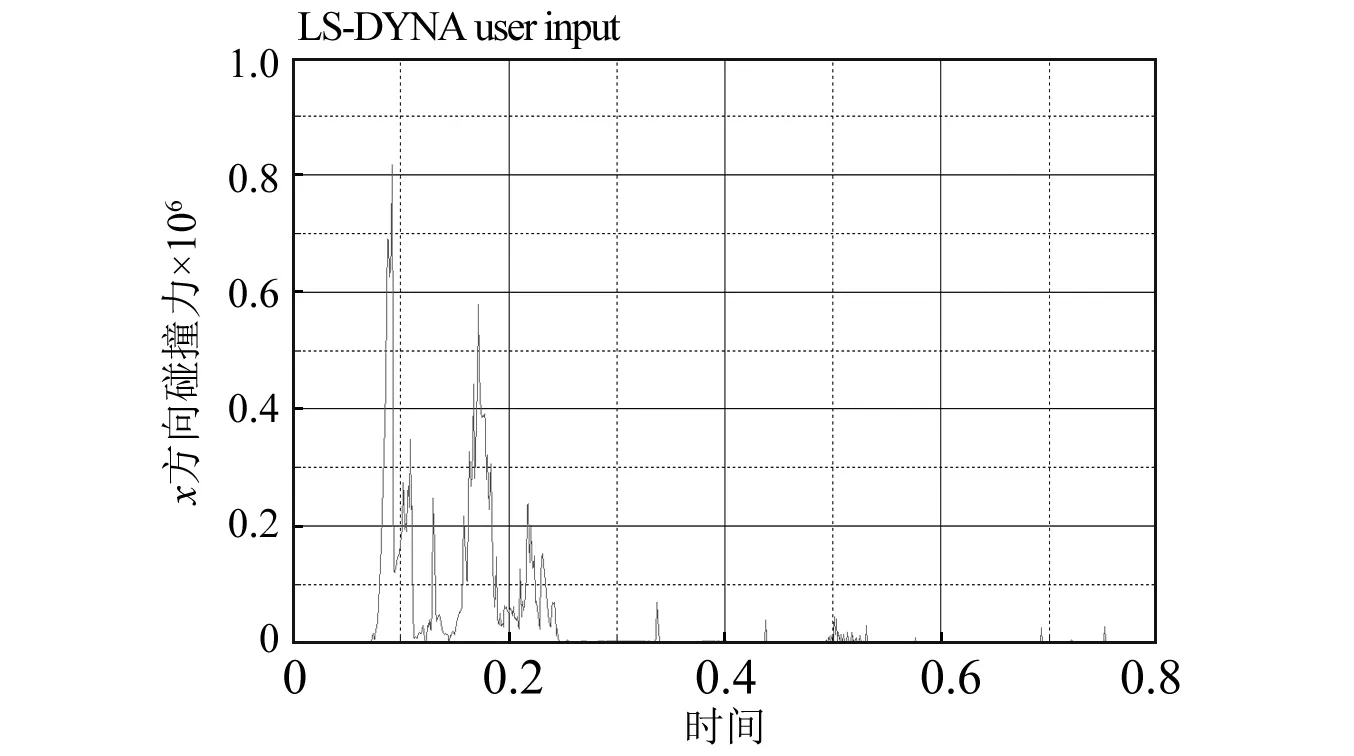
图9 [90/0/90/0/90]铺层下船艏结构x方向上碰撞力曲线Fig.9 Collision force curve of bow structure in x direction under[90/0/90/0/90] layer

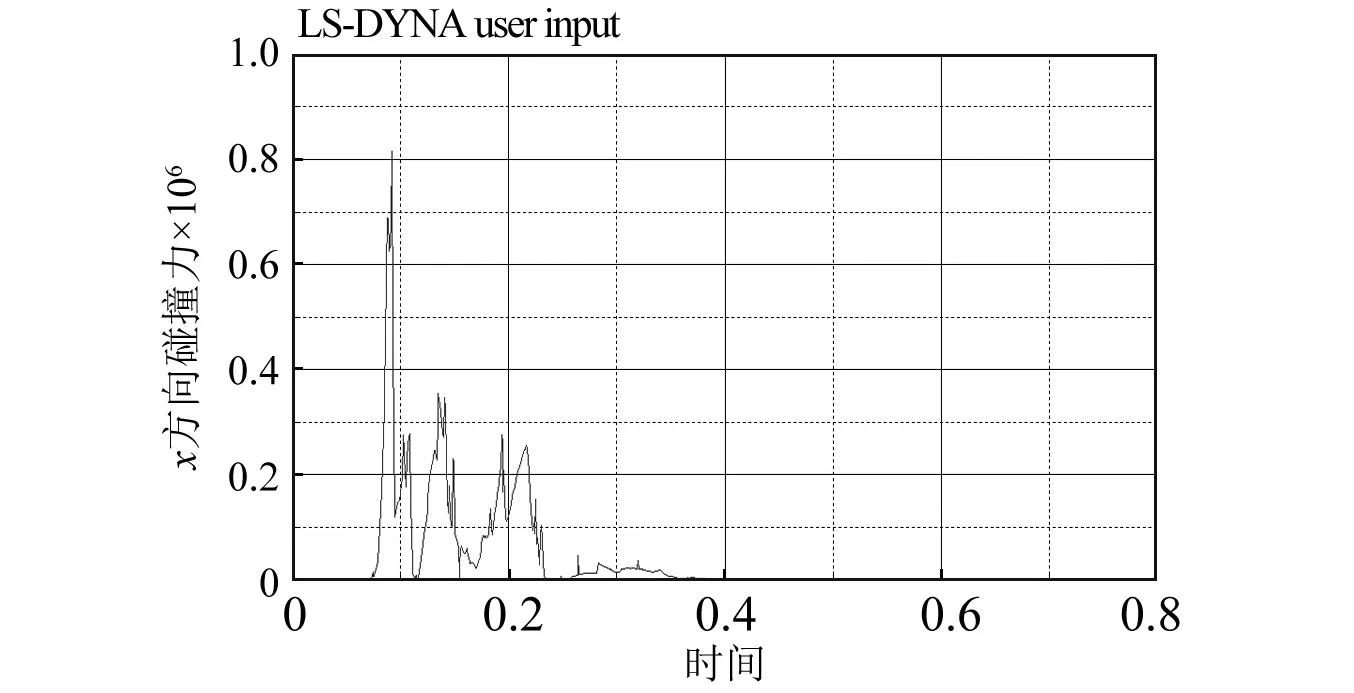
图10 [-45/45/-45/45/-45]铺层下船艏结构x方向上碰撞力曲线Fig.10 Collision force curve of bow structure in x direction under [-45/45/-45/45/-45] layer

图11 [90/0/90/0/90]铺层下船艏结构x方向上速度曲线Fig.11 Velocity curve of bow structure in x direction under [90/0/90/0/90] layer

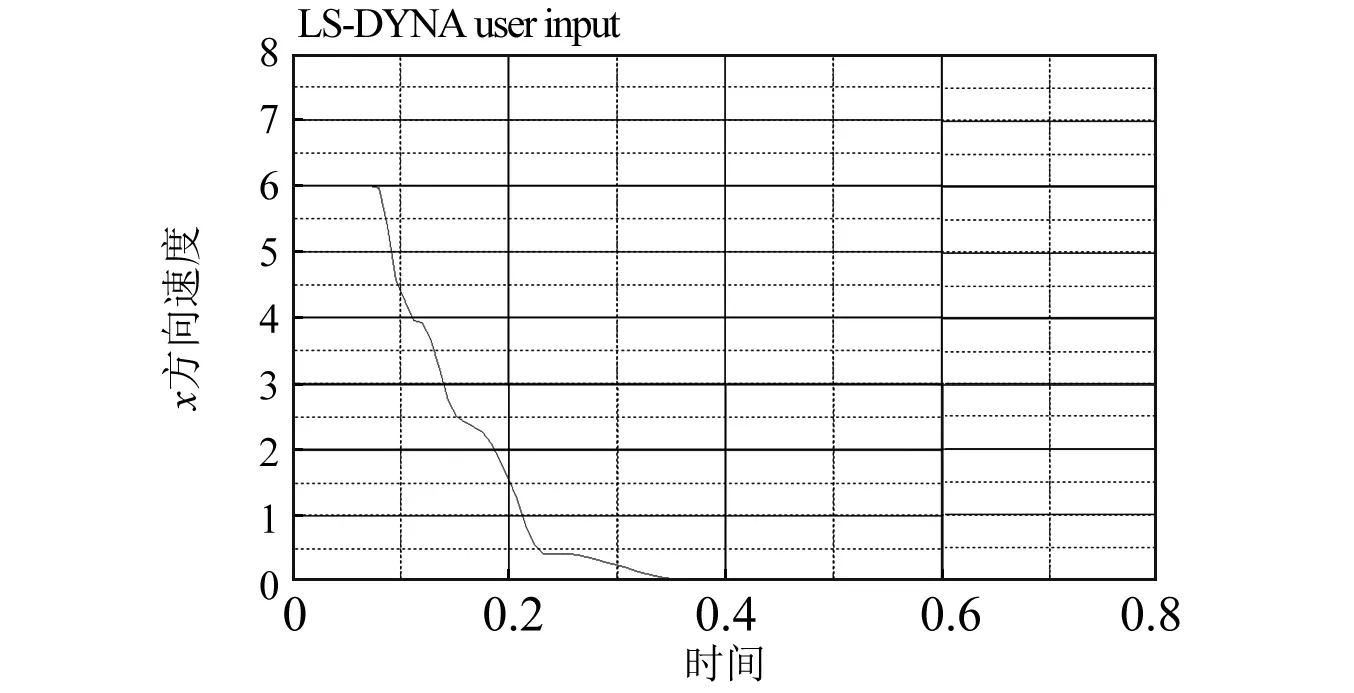
图12 [-45/45/-45/45/-45]铺层下船艏结构x方向上速度曲线Fig.12 Velocity curve of bow structure in x direction under [-45/45/-45/45/-45] layer

图7和8分别给出了[90/0/90/0/90]铺层(以下简称为A类铺层)和[-45/45/-45/45/-45]铺层(以下简称为B类铺层)下船艏碰撞点的有效应力曲线。总体而言，在船-冰首次接触时刻，会出现明显的应力峰值，而后应力在较小的幅值范围内脉动。对比而言，B类铺层在碰撞时的有效应力峰值为1.05×107Pa，而A类铺层在碰撞时的有效应力峰值为0.91×107Pa，前者较后者高大约1.40×106Pa，两者相差15.4%。这种现象出现的主要原因在于玻璃钢纤维材料的力学性能呈各向异性。在[90/0/90/0/90]铺层下，大部分冰载荷方向沿着x方向，则0角度玻璃钢纤维沿轴向承受主要冰力载荷。由于玻璃钢纤维在其轴向的弹性限度内伸长量大且拉伸强度高，故轴向吸能大，因此[90/0/90/0/90]铺层能降低首个应力峰值，能够很好地减轻碰撞瞬间冲击载荷对船艏结构的影响。此外，除首个有效应力峰值以外，B类铺层的有效应力峰值一直小于A类铺层。通过计算可见，B类铺层遭受撞击后在瞬时内会达到更大的应力峰值，对于船舶结构构成更大的风险；而A类铺层可以有效降低首个应力峰值，而将撞击能量转移到后续时间内。

图9和图10分别给出了A类铺层和B类铺层下船艏结构在x方向上遭受的碰撞力曲线，图11和图12分别给出了A、B铺层下船艏结构在x方向上的速度曲线。A类铺层船艏结构在碰撞发生后的首个碰撞力峰值约为8.18×105N，B类铺层船艏结构的首个碰撞力峰值约为8.17×105N，两者几乎相等。结合图11和图12可见，在碰撞发生的初始时刻，船舶在短时间内速度的改变或速度曲线的斜率即加速度基本一致。因为A、B两类铺层船艏初始速度相同，由动量定理不难得到，二者在与冰排碰撞后的首个碰撞力峰值几乎相等。换言之，玻璃钢铺层方式并不影响碰撞力首个峰值大小。B类铺层船舶速度迅速降低到0左右，而A类铺层还将保持0.5 m/s的速度缓慢前行一段时间。相应地，B类铺层的撞击力峰值也不断减小，而A类铺层撞击力相对较大。从图9、图10中可以看出，A、B两类铺层的碰撞力曲线呈现出明显的非线性特征，这是由于船艏在不断侵入冰排的过程中，冰排发生破碎，在数值模拟过程中表现为冰排模型的失效，出现碰撞力卸载现象。

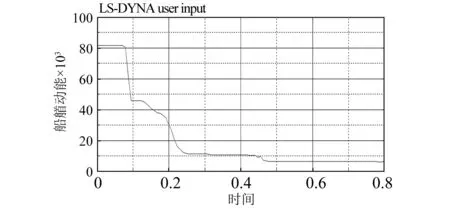
图13 [90/0/90/0/90]铺层下船艏结构动能曲线Fig.13 Kinetic energy curve of bow structure under [90/0/90/0/90] layer

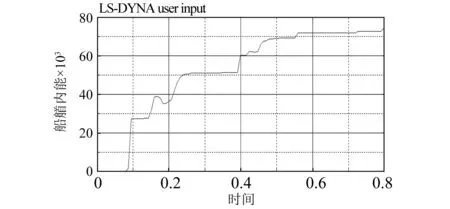
图14 [90/0/90/0/90]铺层下船艏结构内能曲线Fig.14 Internal energy curve of bow structure under[90/0/90/0/90] layer

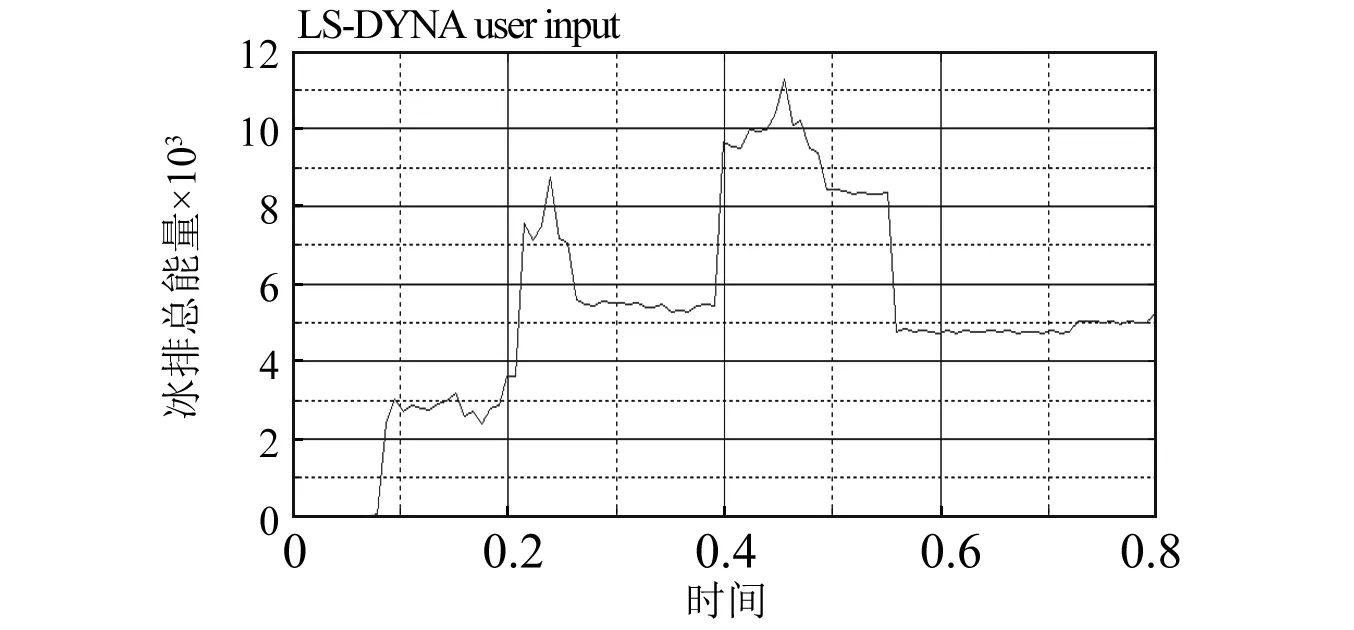
图15 [90/0/90/0/90]铺层下冰排的总能量变化曲线Fig.15 Total energy curve of ice floe

图13～15分别与图7对应的工况下，即[90/0/90/0/90]铺层下，船艏与冰排碰撞后的船艏结构动能、船艏结构内能和冰排动能的变化曲线。从图中可见，船艏在与冰排碰撞过程中，其动能单调递减，总减少量约为7.60×104J，其内能逐渐增加至7.10×104J。冰排的总能量呈现波动状，在碰撞过程中达到最大值，在碰撞结束后反而会有一定的降低，这主要是由碰撞后部分浮冰失效导致的。但总体上冰排能量仍呈现增加，碰撞结束后增加的总能量约为0.50×104J，这部分增加的能量全部来源于船艏结构初始动能，船艏结构动能减少量基本等于内能增加量再加上冰排的总能量，满足能量守恒。

图16为图8对应的工况下，即[-45/45/-45/45/-45]铺层下，船艏与冰排碰撞后的船艏结构动能变化曲线。对比图16和图13可见，[90/0/90/0/90]铺层下船撞击后动能损失小于铺层[-45/45/-45/45/-45]，因此船舶吸收的内能越小，产生的变形能就越小，对船艏结构造成的影响也就越小。此类铺层下船艏内能和冰排总能量的变化趋势与图14和图15类似。

(2)工况二：不同速度下碰撞后船舶受力情况

船-冰碰撞时，船舶速度是影响碰撞结果的主要因素之一，因此本节中研究初始速度对船-冰碰撞的影响。为了研究初始撞击速度对船和浮冰碰撞性能的影响，结合船舶实际情况，船舶初始速度分别设为4 m/s、6 m/s、8 m/s、10 m/s，保持其他求解条件一致，浮冰的初始速度为零，铺层角度设置为[-45/45/-45/45/-45]不变。

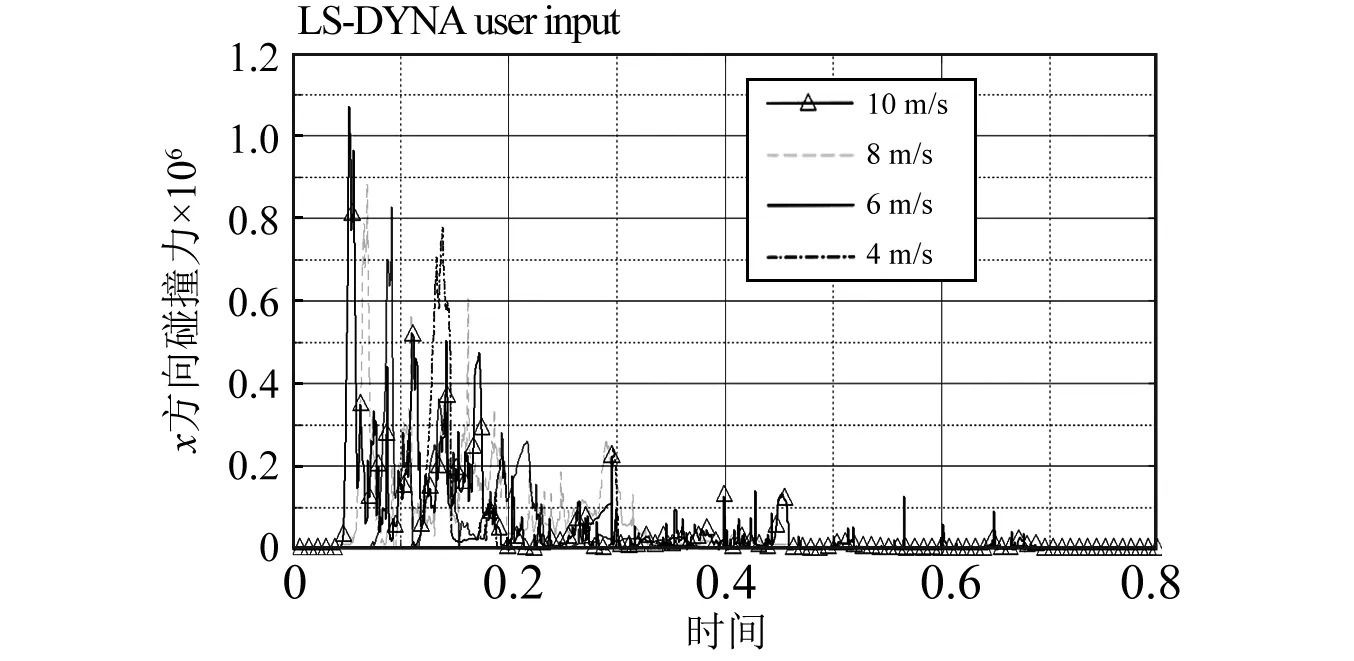
图18 不同速度下船艏结构x方向上碰撞力曲线Fig.18 Collision force curve of ship bow in x direction under different impact speed

图17为船艏上与冰排最早接触的外板单元节点处有效应力曲线，其横坐标单位为秒(s)，纵坐标单位为帕(Pa)。图18为船艏结构在不同速度下x方向上的碰撞力曲线，其横坐标单位为秒(s)，纵坐标单位为牛顿(N)。由图17可见，船体外板上点的有效应力曲线呈现明显的高频脉动现象，曲线局部出现不同的峰值点，并伴随着不断地加载和卸载。对比而言，速度越大船舶外板的有效应力越大，但碰撞力的最大值和船舶速度没有正比关系。从8 m/s和10 m/s的峰值对比可见，在船速较大时，应力峰值将呈现非线性快速增加。由图18可见，船艏结构的碰撞力大小和速度呈正相关。不同速度下船艏碰撞力和有效应力产生差异的原因不完全一致：碰撞力载荷首峰值主要受初始撞击速度影响，而有效应力首峰值的变化则受到初始撞击速度、不同冲击速度下玻璃钢材料的强度和海冰材料强度等多种因素综合影响。

图19表示同一时刻不同速度下船-冰碰撞后冰的破坏应力截图。时刻均选为碰撞发生后0.4 s。从图19中可见船速越高对浮冰造成的破坏越大，同理可知对船舶造成的破坏越大。在真实的船-冰碰撞过程中，海冰的材料属性会受到撞击速度的影响，例如海冰随加载速度的升高可能呈现韧性、韧脆过渡、脆性等特性[16]，所以不同撞击速度下，海冰材料强度的改变对于冰船相互作用可能会有很大影响。但在本文数值模拟中，所有碰撞工况下海冰的材料属性均保持一致，因此在不同碰撞速度下，不考虑海冰材料属性对碰撞的影响。

5 结论

本文通过ANSYS/LS-DYNA软件，对玻璃钢船与冰排发生碰撞的过程进行了仿真，经过对比和分析，得出如下的结论:

(1)在同一速度下船舶与冰发生碰撞，不同的铺层方向对其应力有显著的影响，[90/0/90/0/90]铺层下撞击时峰值应力小于[-45/45/-45/45/-45]铺层，二者相差约15.4%，研究表明[90/0/90/0/90]铺层下0角度玻璃钢纤维轴向承受主要冰力载荷，有利于降低首个应力峰值，将碰撞能量转移到后续的时间内，说明[90/0/90/0/90]这种铺层方式在碰撞发生时有利于保护玻璃钢船艏结构，能避免玻璃钢船艏在与冰排碰撞瞬间发生变形达到极限屈服应力而失效破坏。

(2)不同铺层角度下，同一初始速度船舶的碰撞力首峰值几乎保持一致。后续过程中，船舶初始动能在不断减小，而内能即变形能在不断上升。冰排的总能量呈现波动式上升，能量峰值在碰撞结束前的一段时间处，此后因部分浮冰的失效，能量反而有所降低。船舶动能的减少量最终转化为船舶的内能和冰排的能量，系统的总能量保持守恒。

(3)碰撞结果显示，[90/0/90/0/90]铺层下船撞击后动能和速度损失小于铺层[-45/45/-45/45/-45]，结合结论(1)和(2)可知，此时船舶吸收的内能也越小，变形越小，受到的损害也越小，再次表明[90/0/90/0/90]铺层方式有利于保护船舶结构。