基于浸入边界算法的振动二维矩形柱绕流模拟研究

杨 青， 曹曙阳， 周军文

(1. 安徽建筑大学 土木工程学院，合肥 230601; 2. 同济大学 土木工程防灾国家重点实验室，上海 200092;3. 常州工学院 常州市建设工程结构与材料性能研究重点实验室，江苏 常州 213032)

振动钝体绕流是一类具有广泛工程应用背景的流固耦合问题，其普遍存在于大跨桥梁结构、高层建筑以及风力发电设备中[1-3]。柱体作为上述各类结构中常见的钝体断面形式，更是成为此类基础研究领域的重点。

早期振动柱体研究多借助于风洞试验完成[4-5]，近年来，随着计算理论和硬件设备的发展，越来越多的学者倾向于利用CFD技术研究此类绕流问题。

Singh等[6]利用有限体积法模拟雷诺数Re=100和150时，不同强迫振动频率下的方柱绕流，详细分析了方柱锁定区内的气动系数及流场特征；Placzek等[7]采用有限体积方法模拟出Re=100时强迫振动的二维圆柱绕流，通过柱体升力系数随振动频率和振幅的变化曲线分析柱后尾流特征；国内徐枫、欧进萍[8]则借助Fluent研究Re=150时不同截面形状对柱体振动形式的影响；丁林等[9]进一步在高雷诺数范围(30 000≤Re≤110 000)展开不同截面形式柱体流致振动问题的研究，发现柱体流致振动振幅和频率与尾迹旋涡形态紧密相关；刘志文等[10]采用“刚性运动区域+动网格区域+静止网格区域”的思路建立网格，利用Fluent对宽高比为4的矩形断面涡激振动响应进行了数值模拟，其研究结果与已有文献风洞试验结果的吻合性，证明了Newmark-β方法结合动网格技术的可行性。

然而，传统CFD技术在求解振动钝体绕流问题时，多需借助动网格技术，计算耗费较高。相比之下，浸入边界方法(Immersed Boundary Method，IBM)利用力源拟化边界的思想，直接可在静止网格体系中实现振动钝体的边界再现，略去网格再生步骤，能够显著减轻计算负担，且保证较好的计算精度。Luo等[11-12]从此类算法理论基础入手，致力于提高此类方法在动态钝体数值求解的精度；Chern等[13]则利用IBM模拟圆柱在Re=100～300时两种不同自由度(竖向及扭转)设置下的风致振动，研究发现：单一竖向自由度工况时，圆柱在锁定区初始时刻，振动较大；双向自由度工况时，圆柱尾部流场涡型由P型向2C型转换；钟国华等[14]也基于IBM研究了均匀流场中圆柱的振动问题，研究显示：圆柱阻力在运动过程中一直存在振荡，在最大振幅位置处，阻力与已有数据对比，呈现较大的数值差异。

综上所述，振动柱体绕流研究目前仍多集中于方柱、圆柱等基本外形，对于实际建筑结构中同时出现“分离”和“再附”现象的钝体断面，则鲜有涉及。IBM虽然可以更高效地应用此类结构绕流的研究，但因其早期过多关注于算法改进，现有文献仅在轮机、活塞等工程简化研究问题中作出尝试[15-16]，少有针对土木结构流固耦合绕流模拟的应用。因此，系统地开展不同边长比下振动柱体的绕流研究，具有较高的工程应用价值。

本文基于IBM核心概念，编写了数值计算模型，在Re=1×103时，展开不同边长比下竖向强迫振动矩形柱的绕流研究，其中柱体运动轨迹为y(t)=Asinφ=Asin(2πfct)，式中y(t)为物体轨迹，A为振幅，fc为振动频率，t为时间。模拟中振幅恒定为柱体迎风面高度的14%，以便同已有文献数据结果对比。柱体边长比B/D=1，3，5，分别对应柱体流动完全分离阶段及再附阶段。通过涡脱锁定区、流场特征、气动力系数三个方面的讨论，研究不同边长比下振动柱体的绕流，丰富IBM在工程领域中的基础研究。

1 数值模型

本文数值模型以IBM为基础，结合双线性插值(Bi-linear interpolation method)和内部流体处理方法(Internal flow treatment)，以实现不同边长比柱体的强迫振动绕流模拟。下文即对对该数值模型展开详细介绍。

1.1 IBM控制方程

IBM利用流体与物体边界相互作用的力学概念，将物体边界简化为作用于边界点上的力源，并引入至Navier-Stokes方程中参加流场迭代计算，进而演化出边界的几何形状和物理特性(式(1)～(2))：

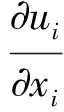
(1)

(2)

式中：ui、uj为流体速度；ρ为流体密度；P为压力；ν为流体运动黏性系数；Fi即为边界力源，施加于图1中边界点上。

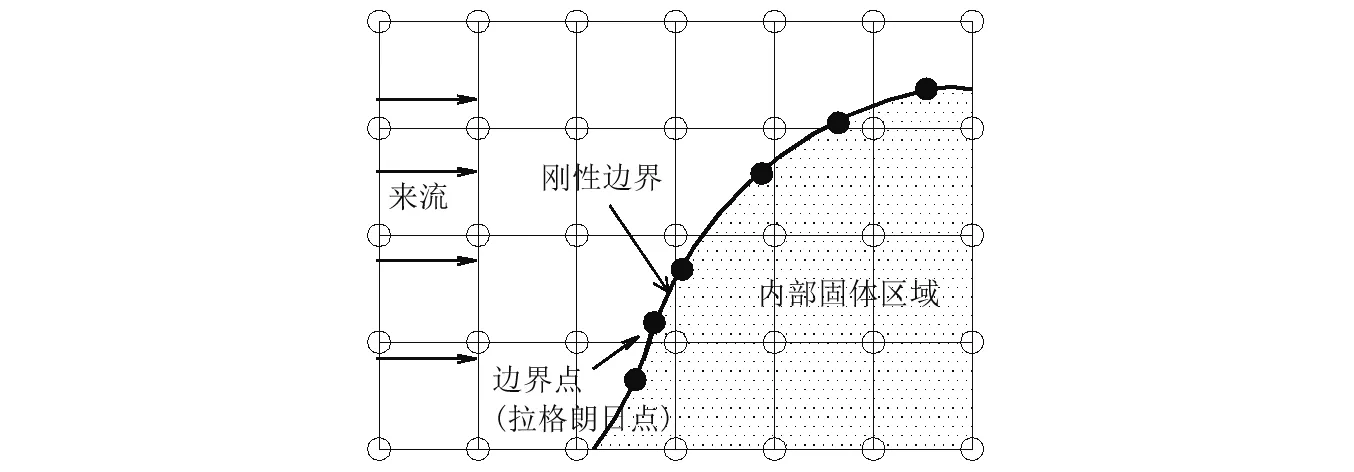
图1 浸入边界示意图Fig.1 Illustration of immersed boundary

边界力源Fi采用反馈构造形式，其力源概念更加清晰，反馈循环的应用也使其能够实现较高的边界数值精度，计算式为

式中：αf和βf为反馈系数项，其取值直接关系到边界拟化效率；ui(sur)为边界控制点处流体速度，由流体控制方程计算得出；Vdesired为物体边界设定速度，静止状态时其值为零，若物体处于强迫振动状态时，Vdesired可由振动方程计算得出；ui(sur)-Vdesired为边界处流体速度与边界设定速度的差异，表达式(3)正是基于此差异，通过反馈系数回馈出边界力源使两者速度接近，以满足无滑移刚性边界条件。内部流体则选用自由发展方法展开处理。

1.2 振动边界实现技术

IBM模型的计算核心在于获取实时边界控制点处流体速度ui(sur)，用以构造边界力源，进而迭代出钝体外形。本次模拟对象为振动边界，且计算网格采用交错网格，边界控制点很难与速度网格点重合，如图2所示。

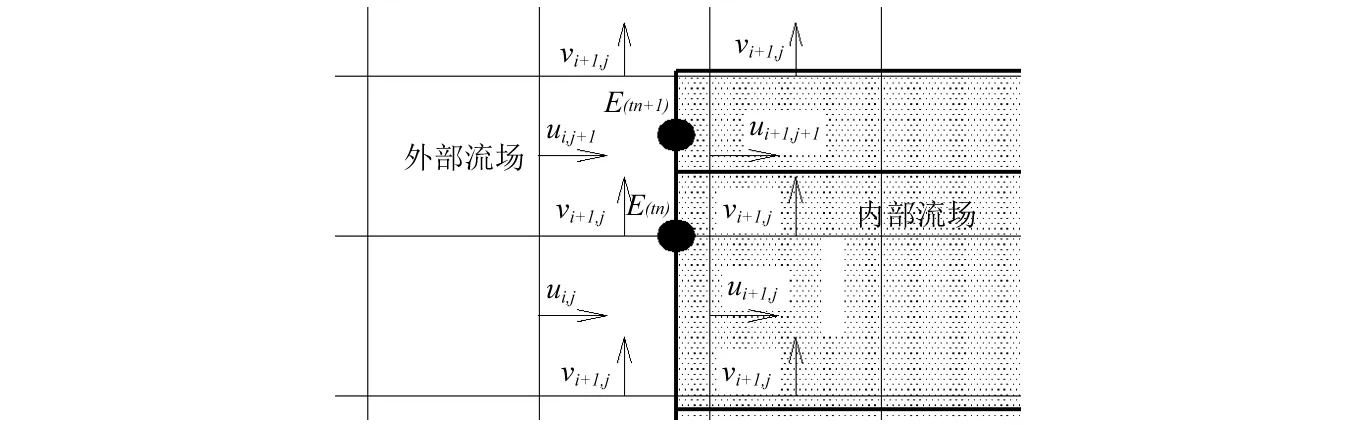
图2 振动边界示意图Fig.2 Illustration of oscillating boundary

图2中振动状态下的边界控制点E位置随时间发生改变(Etn—Etn+1)，此时边界速度不能由流体控制方程直接求得。因此，为保证边界控制点速度的实时获取，需借助本节开始所介绍的双线性插值方法完成周围速度网格定义点与边界控制点之间的数据传递。

双线性插值方法，其过程分为两个步骤：速度获取和力源分配。

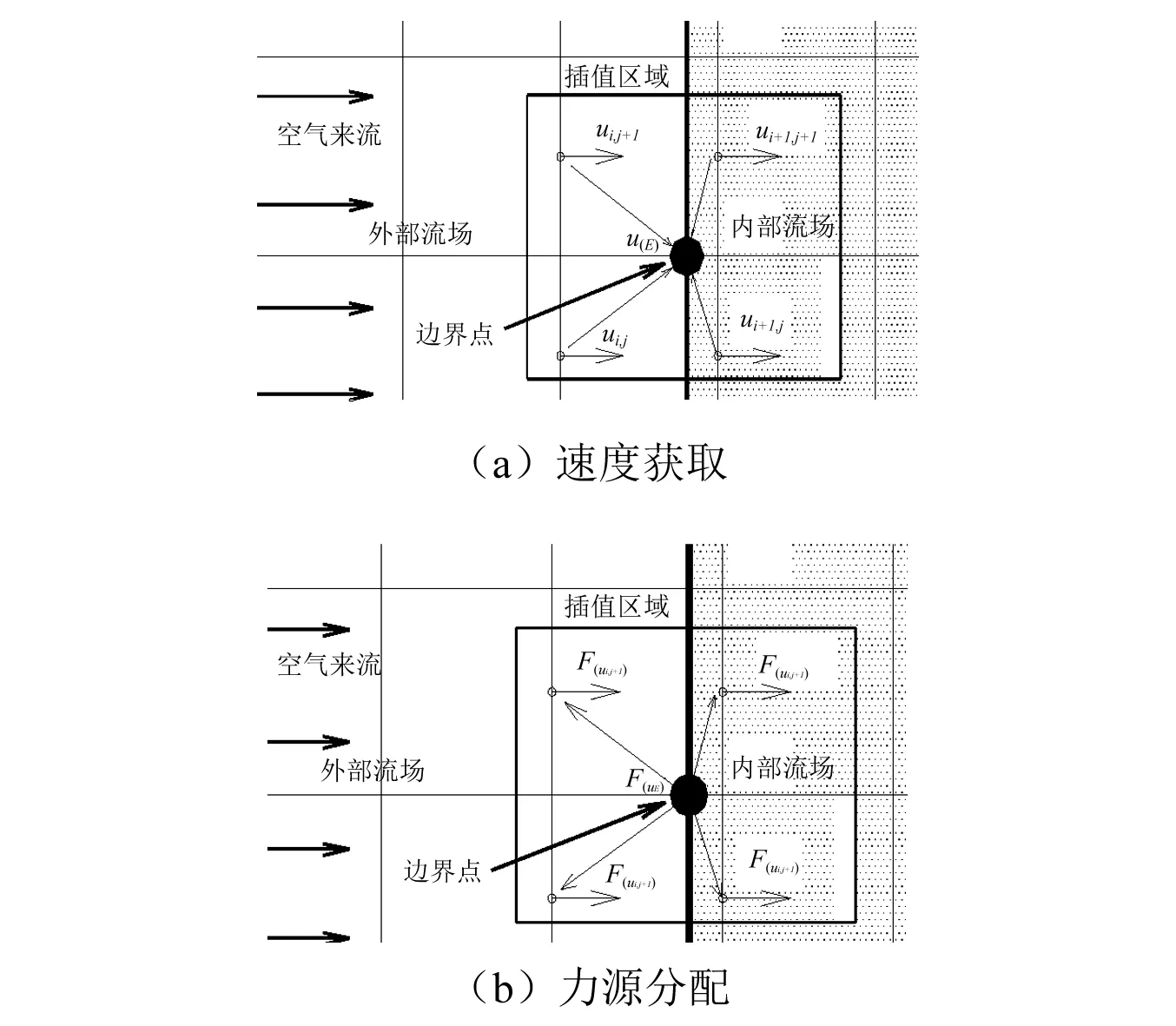
图3 双线性插值方法示意图Fig.3 Illustration of bilinear interpolation method

其中速度获取如图3(a)所示，边界控制点速度u(E)可由周围速度定义网格点插值得出，具体插值公式为

(4)

式中：ui,j为插值所需速度网格定义点；φi,j为在插值过程中起到关键作用的双线性函数，其一般形式为

(5)

式中:Δ(xi)和Δ(yi)为二维计算网格间距；(xE,yE) 为边界控制点E所处坐标; (xi,yi) 则表示为各插值点坐标值。

力源分配则是指力源在边界点构造完成后再分配到周围速度定义网格点上参与计算的过程。图3(b)为该步骤示意图。

F(ui,j)=φi,jF(uE)

(6)

式中:F(uE)为边界控制点力源项；F(ui,j) 为插值网格点处力源值;φi,j为式(5)所示，表示双线性函数。

具体至本文振动矩形柱绕流模拟，首先设计出定位模块，根据物体振动轨迹计算出某一瞬时边界点的运动坐标，其次依据插值方法迅速确定边界点周围的速度定义点，利用边界插值函数获得边界点处流动参数以构造边界力源，最后再将边界力源分配到周围速度网格定义点上，以参与该瞬时流场的整体计算，进而实现对运动边界的拟化。图4为本文振动边界实现技术流程图。

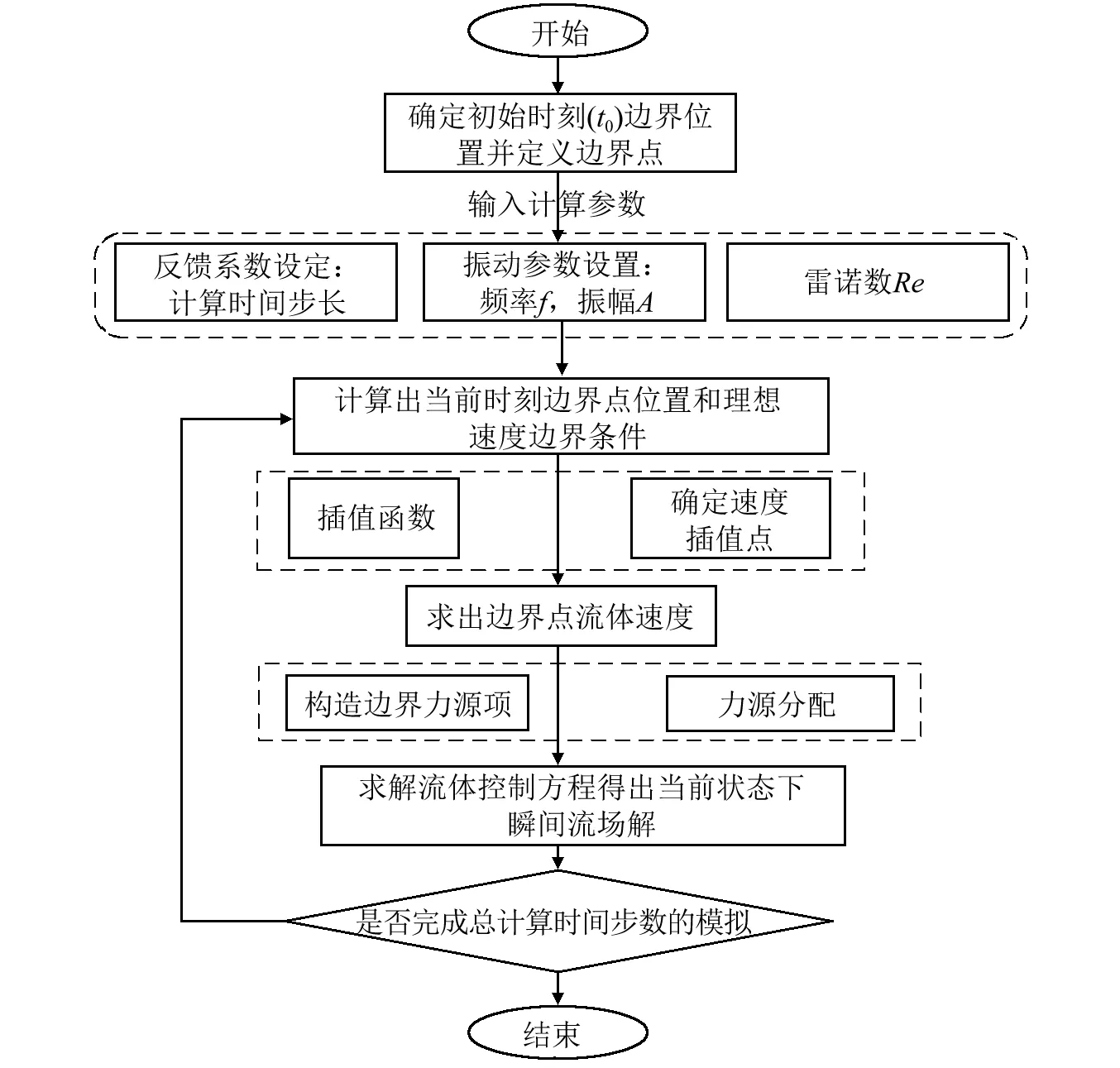
图4 振动边界实现技术流程图Fig.4 Sketch of realization technique for moving Boundary

2 绕流计算域说明

本次振动矩形柱绕流均采用二维非均匀计算网格。流体从计算域左端施加，流动从左至右。边界条件统一设定为：入口边界条件u=1.0，v=0；出口边界条件采用对流边界条件：∂u/∂t+um▽u=0；即流动变量除压力项外其余的边界梯度值为零。上下边界条件设定为无摩擦边界：∂u/∂y=0; ∂P/∂y=0;v=0。力源反馈系数取值为αf=-1.6×105；βf=-60。

柱体绕流计算域中，特征尺寸取为柱体迎风面高度D，计算区域中入口距方柱中心距离为10D，出口边界则设置为31D。上下计算域边界长度为H，D/H设定为1/28。考虑到方柱运动轨迹为竖向强迫振动，为增强柱体表面流动细节的捕捉，在其宽度B范围内，沿零时刻柱体上下表面各设置尺寸为D×B的均匀网格区域，格子大小统一选为0.01D。超出此区域，则设置拉伸网格，网格总数为412×242；时间间隔Δt为1.5×10-4，计算域布置如图5所示。

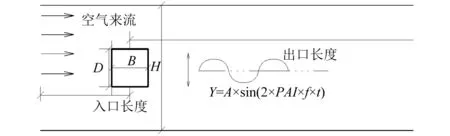
图5 振动方柱计算域示意图Fig.5 Illustration of calculation domain for oscillating rectangular

3 数值验证

为验证本文程序可靠性，首先利用该动态程序模拟Re=103，A=0，边长比B/D=1的静止方柱绕流。

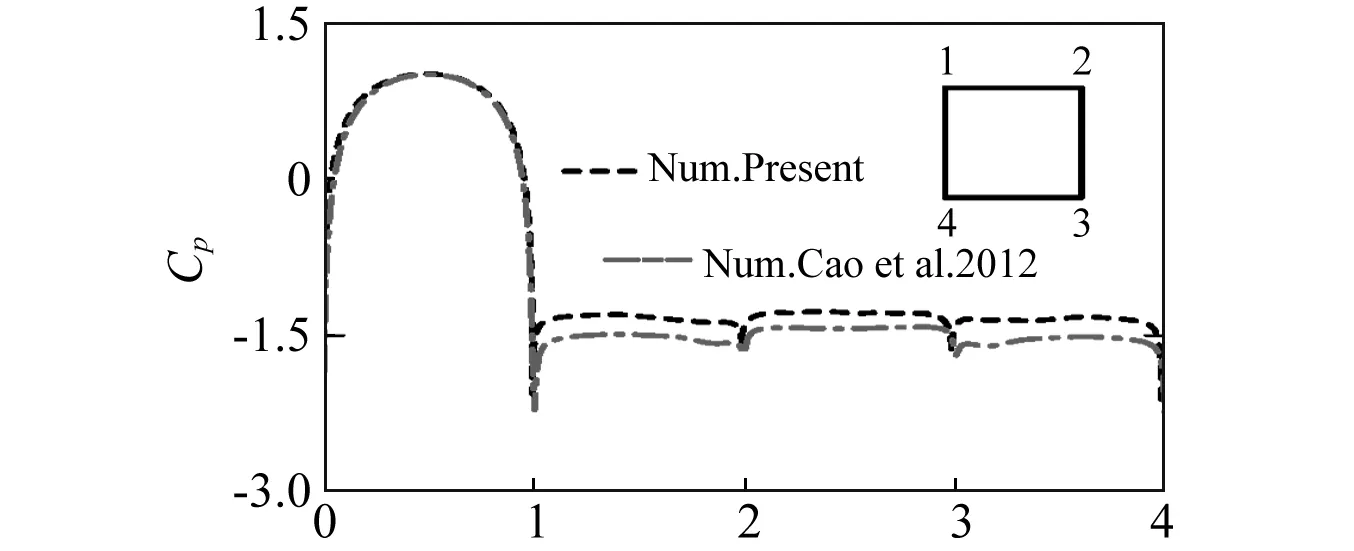
图6 方柱时均化表面压力分布曲线Fig.6 Distribution curve of mean pressure coefficient Cp for square cylinder at Re=103

图6为Re=103时方柱表面压力分布。图中可以看出柱体前缘表面压力分布与Cao 等[17]数据基本吻合，方柱其余表面压力分布特征亦吻合较好，但其值略大。原因可能存在于本文模拟为二维模拟，模拟维度的不同导致了流动分离时流场结构的差异性变化，进而影响到方柱表面压力分布。

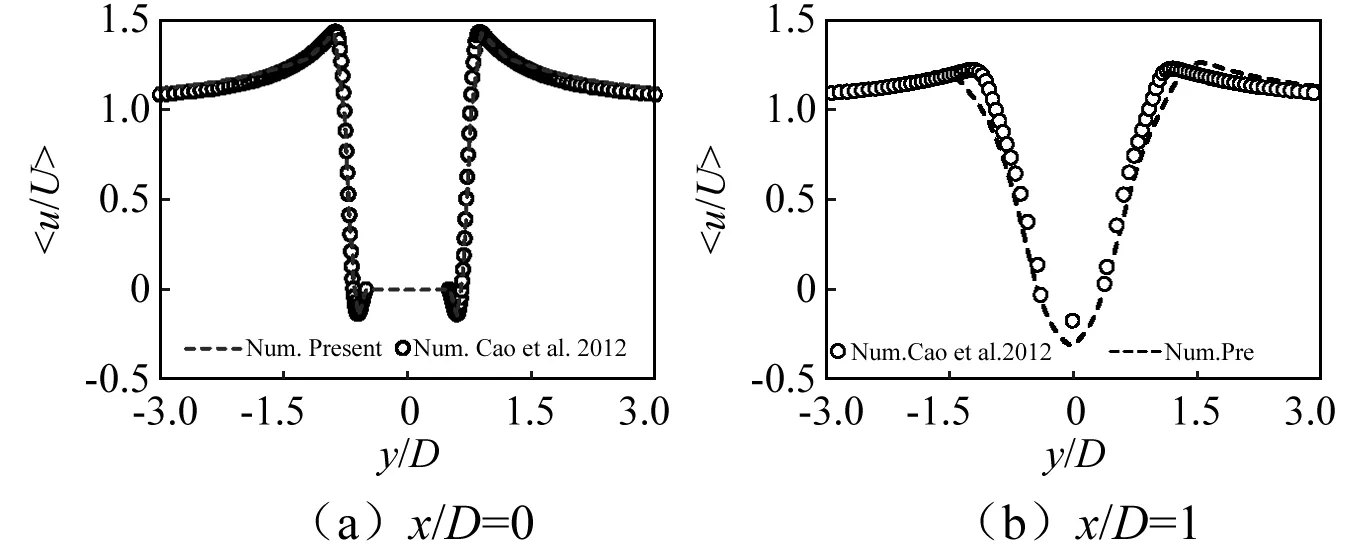
图7 方柱尾流区时均流向速度分布Fig.7 Mean stream velocity in wake region of square

图7为方柱尾流区平均流向速度分布，U为入口参考流速。图7(a)中x/D=0处方柱平均流向速度分布，由于其在钝体尖锐边角的流动分离会而造成的分离层内压力下降，导致尾流区流体的动量亏损，尾流区内速度减小，在偏于中心线的部分存在速度最小值；图7(b)中x/D=1处，由于已经远离方柱，此效应减弱，速度经过展现延伸后，趋于回归到来流风速。方柱此时模拟所得St为0.133，与Cao等所得结果0.129基本吻合。

在此基础上，展开模拟Re=103，A=0，边长比B/D=5的方柱绕流。

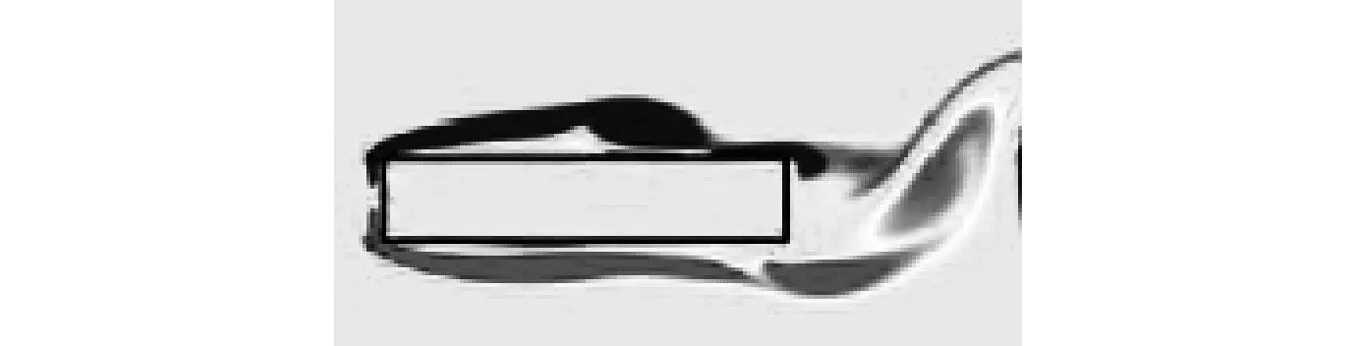
图8 矩形柱涡量图(B/D=5)Fig.8 Vortex contour of rectangular (B/D=5)

图8为边长比B/D=5的矩形柱涡量图。此时，矩形柱绕流已完全进入冲击剪切层阶段，柱体侧面附着涡形状不再稳定，涡脱结构更加复杂。柱后流场结构完全由柱体前缘流动分离所决定。本文模拟所得流场特征图符合Nakamura等[18]的研究描述。

进一步将本次模拟所得不同边长比矩形柱斯托罗哈数St(D)(Re=103)与Nakamura等对比，如表1所示，可以看出，本文数值结果吻合较好。

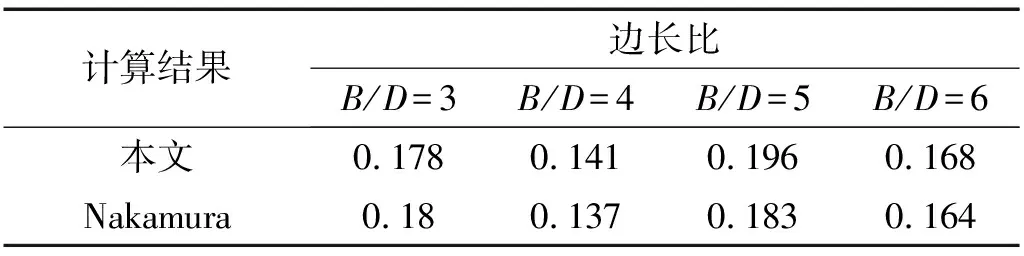
表1 不同边长比矩形柱St(Re=103)

上述各类计算数据的吻合验证了本文IBM算法程序的可行性和准确性。

4 振动柱体绕流模拟

振动矩形柱绕流计算中，关键无量纲参数包含：Stc=fcD/U，Stv=fvD/U，Stn=fvnD/U；其中fc为强迫振动频率，fv为振动柱体涡脱频率，fvn则代表静止涡脱频率；D为柱体高度；U为来流速度。

本节着手展开Re=1×103，振动频率Stc=0～0.5、振幅A=0.14D的不同边长比(B/D=1，3，5)强迫振动柱体的绕流模拟，分析柱后尾流涡脱特征，并结合柱后近尾迹流场显示、气动力系数以及气动稳定性三个方面，探索边长比效应对振动柱体绕流气动特征的影响。

4.1 涡脱频率分析

本次模拟参照Nakamura等的试验设置，亦在柱体后部1.5D处设置速度观测点，用以收集流场速度时程数据，通过对其作频谱分析，绘制出振动矩形柱尾流涡脱随振动频率变化的曲线。

图9 方柱涡脱随振动频率变化曲线(B/D=1)Fig.9 Variation of frequency ratio for squares with varying oscillating frequencies(B/D=1)

图9为方柱涡脱随振动频率变化曲线，通过速度频谱分析得出其锁定区长度(Lock-in region length)为0.06～0.2。当外加强迫振动频率Stc超过0.2时，柱体尾流涡脱频率回归静止涡脱的现象十分突出，并一直保持，使得振动频率与涡脱频率的比值(Stc/Stv)呈线性分布特征。本次模拟主要特征与Singh等得出的现象吻合，验证了本次模拟的可靠性。Taylor等[19]定义锁定区中Stc=Stv=Stn的点，为共振锁定点(Resonant point)，此时外加振动频率与静止涡脱频率完全保持一致，本次模拟中方柱(B/D=1)共振锁定点为0.133。

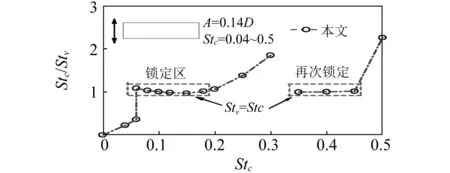
图10 B/D=3时柱体涡脱随振动频率变化曲线Fig.10 Variation of frequency ratio for rectangular(B/D=3)with varying oscillating frequencies

图10为B/D=3时矩形柱涡脱随振动频率变化曲线。图中可以看出：与振动方柱对比，矩形柱(B/D=3)涡脱亦在外界振动频率Stc=0.06时进入锁定区，柱体尾流涡脱频率与外界振动频率保持一致；当振动频率提升至Stc=0.2时，柱后尾流旋涡脱锁，振动柱体涡脱频率回归到静止时涡脱频率(Stn=0.178)；但不同于方柱(B/D=1)，此后继续增大强迫振动频率，至0.35时柱体再次进入锁定区，出现了呼和敖德同类试验所指出的多级锁定现象[20]，并一直持续到Stc=0.45，此后柱后尾流涡脱再次脱锁并接近静止涡脱频率。

图11 观测点速度频谱图(B/D=3)Fig.11 Frequency spectrum of observation point’s velocity(B/D=3)

图11为矩形柱(B/D=3)尾流速度频谱分析图，图11(a)可以看出Stc=0.25时，静止涡脱频率在尾流流场中起到控制作用，虽然振动频率响应部分也有明显的峰值，但仍小于静止涡脱频率部分，符合超越锁定区后的脱锁现象。图11(b)Stc=0.35时，强迫振动频率已基本控制柱后尾流涡脱，静止涡脱频率部分对柱后尾流涡脱的影响远小于外界激励部分。此前研究振动柱体绕流的文献，多集中于运动振幅增加对方柱涡脱频率、气动力系数的影响，鲜有对于边长比效应在此方面的研究。Nakamura等[21]虽然对不同边长比柱体的相位差、升力系数频响虚部值展开了分析，也并未明确标示出不同边长比下柱体涡脱锁定区情况，但其研究中升力系数频响虚部值两次转正的现象也从侧面说明柱后尾流涡脱多级锁定的情况。

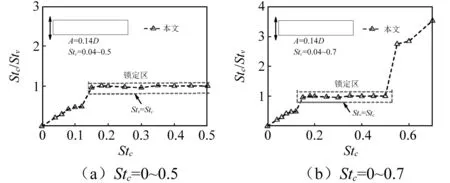
图12 边长比B/D=5柱体涡脱随振动频率变化曲线Fig.12 Variation of frequency ratio for rectangular(B/D=5)with varying oscillating frequencies

继续增大边长比至B/D=5，频谱分析其速度时程，得出涡脱随振动频率变化曲线，如图12所示。图中可以看出，柱体在强迫振动频率Stc=0.15处才开始进入锁定区，此时柱体涡脱频率完全由外界振动频率所控制；锁定区长度有所延长，Stc=0.5时柱体涡脱频率仍处于锁定区；强迫振动频率升高至Stc=0.6时，柱体尾部旋涡已经脱锁，静止涡脱频率重新控制尾流流场。

4.2 流场显示

流场显示对于分析不同强迫振动频率下钝体近尾迹流场特征十分重要，除此之外，流场显示还可用以分析钝体在不同振动频率下的气动力系数特征，揭示锁定区尾流涡脱作用的流动机理。

图13为Stc=0.1时振动相位分别为6π、8π的方柱流场涡量图，结果显示：柱后涡脱频率与强迫振动频率保持一致，柱后涡脱基本呈现周期性再现。

图13 不同相位振动方柱涡量图(Stc=0.1)Fig.13 Vortex contour of squares under different phase(Stc=0.1)

Yang等[22]在振动柱体研究中发现，振动物体涡的放出同运动方向密切相关，物体的运动会抑制同方向涡的产生。图14为本次模拟所得矩形柱不同运动位置处的瞬时涡量图，当物体向上运动时(图14(b))，柱体上侧壁的流动分离则得到明显抑制，外形呈带状，下侧壁流动分离尺寸增大；当物体向下运动时(图14(c))柱体下方的流动分离得到抑制，被压成扁平带状，上侧壁流动分离与零位移位置相比，尺寸增大；零位移位置处(图14(a))柱体上下表面不再明显出现上述流动抑制现象。此流动特征随着柱体振动位置的不同而不断的转换，并影响到尾流区涡脱的放出，使涡脱频率与振动频率逐渐保持一致。Yang等认为这可能就是造成柱体涡脱频率同振动频率锁定的原因。

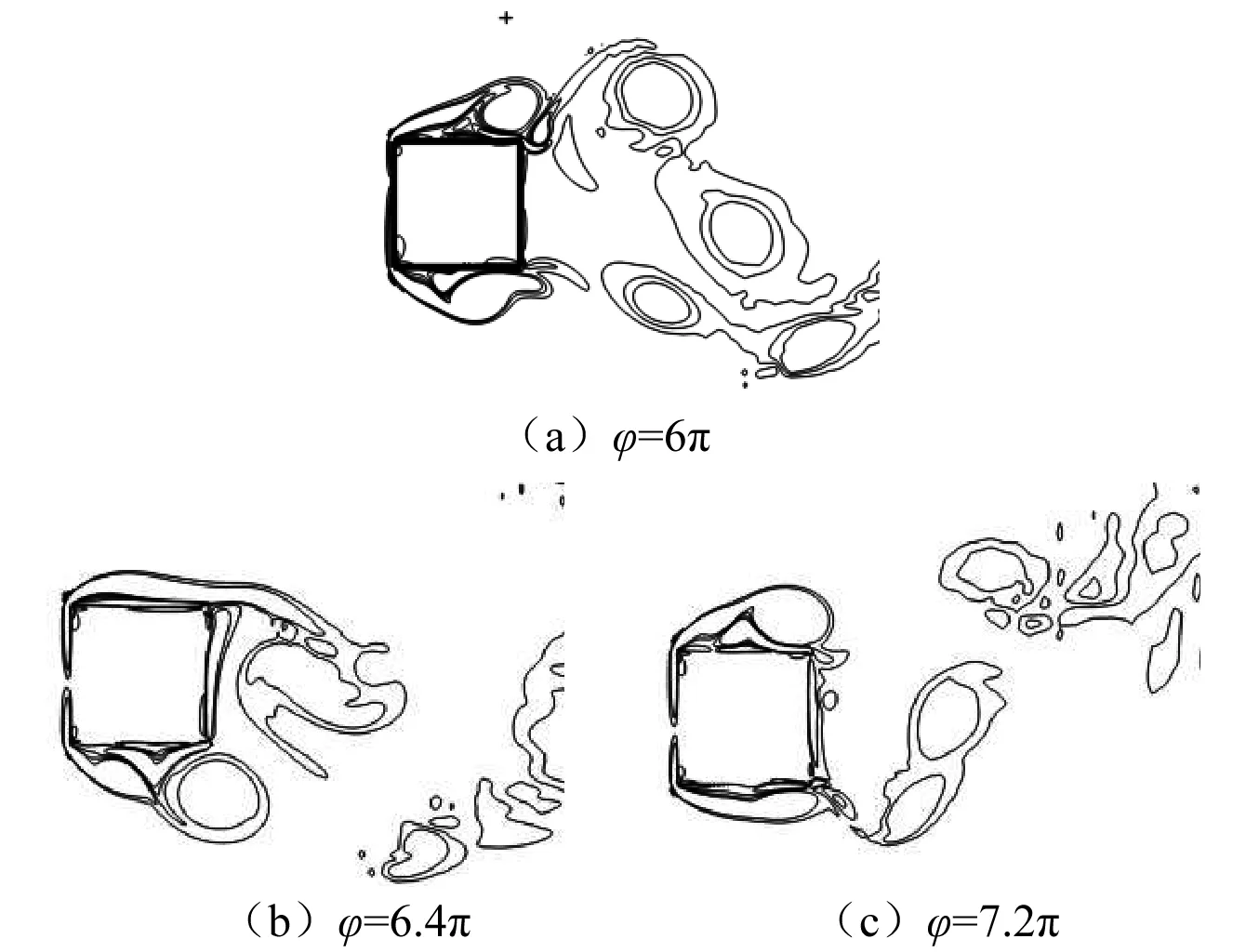
图14 不同运动相位处方柱涡量图(B/D=1，Stc=0.2)Fig.14 Vortex contour of squares at different oscillating phase (B/D=1，Stc=0.2)

图15～16为B/D=3，5时，不同运动相位处矩形柱涡量图。与方柱所得现象相同，柱体表面流动分离特征随着柱体振动位移的不同而不断的转换，并影响到尾流区涡脱的放出，使涡脱频率与振动频率逐渐保持一致；但由于柱体边长比的延长，上述流动特征在运动方向上的影响范围亦会增大，这也可能是涡脱锁定区随边长比变化的原因。

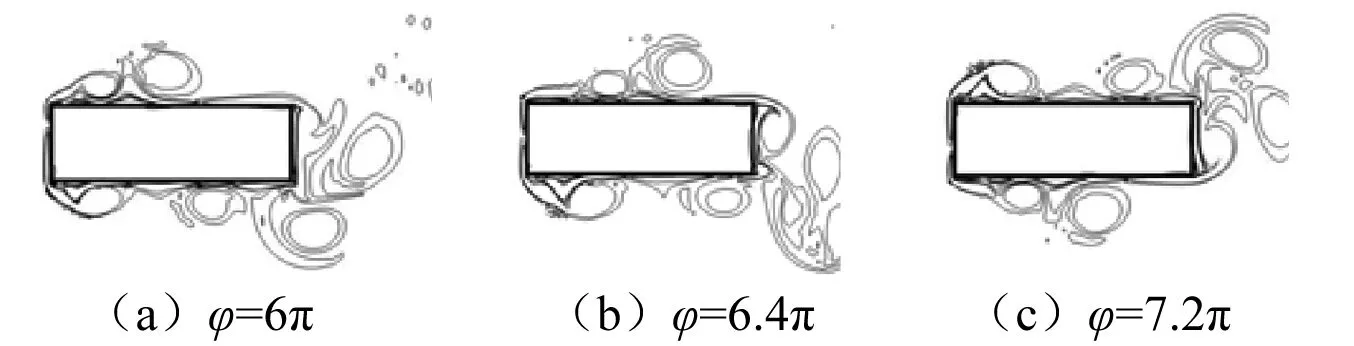
图15 不同运动相位处涡量图(B/D=3，Stc=0.2)Fig.15 Vortex contour of rectangular under different oscillating phase(B/D=3，Stc=0.2)

图16 不同运动相位处涡量图(B/D=5，Stc=0.2)Fig.16 Vortex contour of rectangular under different oscillating phase(B/D=5，Stc=0.2)

4.3 气动系数

图17为强迫振动方柱表面压力分布曲线，强迫振动频率Stc=0.04时，由于外界强迫振动的施加，柱后涡脱加强，此时压强分布表现为较强的吸力，；Stc=0.1时由于柱后尾流流场的转换，柱后压强吸力效应减弱；当Stc=0.15时，强迫振动频率靠近共振锁定点，柱后压强发生跃变，柱后吸力效应突然增强；此后随着外界振动频率逐渐增强，柱体背部表面压强发生较大的减弱，Taylor和Vazza指出这是由于高频振动下，侧壁涡脱和柱后涡脱相互干扰，共同作用的原因。

图17 不同振动频率下方柱时均表面压力分布曲线Fig.17 Distribution of mean surface pressure Cp for squares with varying oscillating frequencies

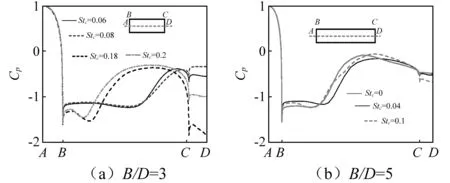
图18 不同振动频率下矩形柱时均表面压力分布曲线(B/D=3，5)Fig.18 Distribution of mean surface pressure Cp for rectangular with varying oscillating frequencies (B/D=3，5)

如图18所示，与方柱相同，边长比B/D=3，5时矩形柱在不同强迫振动工况下，迎风面压力分布曲线基本保持一致；柱体侧面压力分布曲线不再保持均匀分布，出现曲线特征，这可能是由于边长比增大，柱体侧面发生流动分离-再附而决定的；振动频率越高，柱体侧面前缘负压特征越明显，其表面压力曲线分布特征亦同时增强，表明此时柱体侧面涡旋尺寸发生改变，流动分离-再附区长度减小。

图19为矩形柱时均阻力系数随振动频率变化曲线。不同边长比矩形柱阻力系数均在小振动频率处均呈现先上升再降低的趋势；在共振锁定点附近处，阻力系数达到峰值，结合图17～18可看出，柱体背后表面吸力效应均突然加强，此后阻力系数迅速降低。此现象发生原因，可能在于共振锁定点之前，柱后旋涡脱落基本呈现平直脱落的特征，涡脱完全再附于柱体背面(图13)，超出此振动频率时，方柱近尾迹流场特征再次发生改变，涡脱向柱侧角退缩，再附于方柱背面的现象消失(图14)。

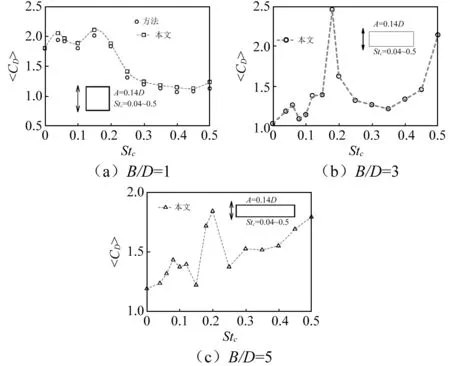
图19 不同边长比矩形柱阻力系数随振动频率变化规律Fig.19 Variation of drag coefficients for different side ratio rectangular with varying oscillating frequencies

5 结 论

本文利用IBM算法模型，在静止网格体系中完成竖向强迫振动柱体的绕流模拟。文章通过设置不同的柱体边长比，从旋涡脱落、流场特征、气动系数等方面入手，探究边长比效应对振动柱体气动特性的影响：

(1)柱体锁定区随边长比的增大而发生变化，在柱体边长比为3时，锁定区出现多级锁定现象，边长比升高至5时，柱体锁定区延长。

(2)柱体运动会抑制同方向涡的产生，并影响到尾流区涡脱的放出；柱体边长比增大后，柱后尾流涡脱影响范围变大，这也可能是不同边长比柱体锁定区发生变化的原因。

(3)边长比B/D=3，5时，矩形柱侧面压力分布曲线不再保持均匀分布，出现曲线特征；振动频率越高，柱体侧面前缘负压特征越明显，其表面压力曲线分布特征亦同时增强，表明此时柱体侧面涡旋尺寸发生改变，流动分离-再附区长度减小；振动工况下，不同边长比柱体阻力系数均在接近自然涡脱频率处(共振锁定点)发生峰值效应。

在此研究基础之上，后期将开展典型桥梁断面的振动绕流数值模拟，利用IBM数值程序的便捷性，增加计算风工程对实际结构的气动特性研究。