多面体外接球的求法

广东 郑荣坤

如果一个多面体的每个顶点都在同一个球面上，那么这个球称为多面体的外接球，这个多面体称为球的内接多面体.求多面体外接球是高考的高频考点，而抽象的空间想象通常让学生一片茫然，因此，“求多面体外接球”也是学生认为较难的考点.虽然它比较抽象,但也不是无法可依,下面笔者归纳常见的解题方法,与读者共勉.

一、长方体(正方体)外接球

由多面体的外接球定义可知，多面体外接球的球心到多面体每个顶点的距离都相等.而长方体(正方体)对角线中点到每个顶点的距离都相等，因此，长方体(正方体)对角线中点就是其外接球的球心.下面给予证明.

已知:如图所示，长方体ABCD-A1B1C1D1中,对角线AC1的中点为O.

求证:OA=OB=OC=OD=OA1=OB1=OC1=OD1.

证明:连接AB1，DC1得四边形AB1C1D如图所示，

四边形AB1C1D为矩形，由矩形对角线互相平分且相等，

得OA=OB1=OC1=OD.

同理容易证:

OA=OB=OC=OD=OA1=OB1=OC1=OD1.

【例1】已知长方体ABCD-A1B1C1D1的所有顶点在一个球面上，若球的表面积为4π，当|DC|·|AD1|的值最大时，则三棱锥B1-ADD1的高为__________.

解析：如图所示，设长方体ABCD-A1B1C1D1的外接球的半径为R，

|AB|=a,|AD|=b,|AA1|=c.

由4πR2=4π，解得R=1.

由长方体外接球的球心为体对角线AC1的中点O，得|AC1|=2R=2，则a2+b2+c2=4.

当且仅当a2=b2+c2时等号成立，

又a2+b2+c2=4，

而三棱锥B1-ADD1的高B1A1的长|B1A1|=|AB|=a,

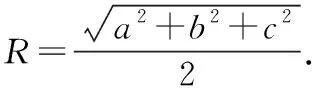
二、补形法

对于一些比较特殊的多面体，将其放入长方体(正方体)中，当多面体的每个顶点都为长方体(正方体)的顶点时，多面体的外接球就是所放入长方体(正方体)的外接球，称这种求多面体外接球的方法为补形法.特殊三棱锥(柱)、四棱锥(柱)外接球的求解常采用补形法，下列以三棱锥为例，说明如何利用补形法求解特殊多面体的外接球.

1.“垂角”三棱锥

“垂角”三棱锥:侧棱垂直于底面，底面是直角三角形的三棱锥就称为“垂角”三棱锥.

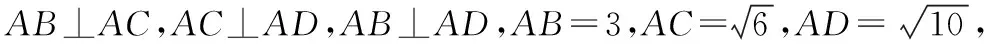
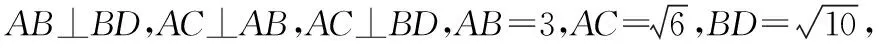
【评注】将“垂角”三棱锥补为长方体，长方体的外接球为该三棱锥的外接球.这样一来，“垂角”三棱锥外接球的求解自然有法可依.除了“垂角”三棱锥之外，求解“侧棱垂直于底面，底面是矩形的四棱锥”的外接球也常采用补形法，还有求解“底面是直角三角形(矩形)的直三棱柱(直四棱柱)”的外接球也常采用补形法.

2.“棱面”三棱锥

“棱面”三棱锥：由长方体的一条棱和一条对角线所形成的三棱锥就是“棱面”三棱锥，它的四个顶点所成空间四边形中恰有三个直角.

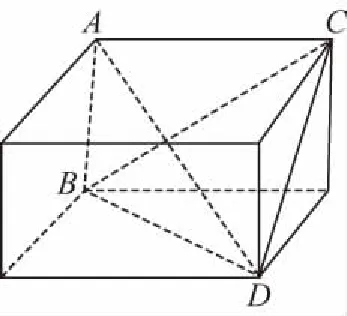
【评注】将“棱面”三棱锥补为长方体，长方体的外接球为该三棱锥的外接球.但在操作过程中，务必选好四面体中的一组对棱，其中一条要同时垂直于两条异面棱，将这条棱作为长方体的棱，它的对棱作为对面的对角线.例如上述例题，由于AB⊥BD，AB⊥AC，则把AB作为长方体的侧棱，AB对棱CD作为长方体一个面的对角线，由于AC⊥CD，则把AC作为长方体的另一条侧棱，进一步确定棱CD在长方体中的具体位置.

3.“对等”三棱锥

“对等”三棱锥：三组对棱分别相等，三棱锥的六条棱可以看成是长方体六个面的面对角线.

【评注】三棱锥中两条相对棱为一组，将其六条棱分为三组，如果每一组中两条相对的棱相等，那么将其补形为长方体，长方体的外接球为该三棱锥的外接球，但在操作过程中，应该将三棱锥的棱作为长方体的面对角线.

三、截面法

利用球截面小圆的圆心和球心连线与截面垂直的性质.先找球截面小圆的圆心，再连接截面小圆的圆心与球心，从而构造直角三角形来求解.

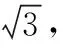
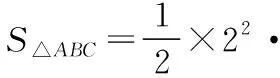
【评注】正三棱锥或正四棱锥的外接球的球心落在锥体顶点与底面几何图形外接圆的圆心的连线或延长线上，求“正三棱锥或正四棱锥”的外接球常采用截面法.先找截面几何图形的圆心，再连接截面小圆的圆心与球心，从而构造直角三角形来求解，其中截面几何图形外接圆的半径长可利用正弦定理来计算.求“正三棱柱或正四棱柱”外接球也常用截面法，连接正三棱柱或正四棱柱的上下底面外接圆的圆心，以两圆心为端点的线段中点就是其外接球的球心.

四、性质法

直角三角形斜边的中线等于斜边的一半，利用这个性质来确定球心位置的方法就称为性质法.

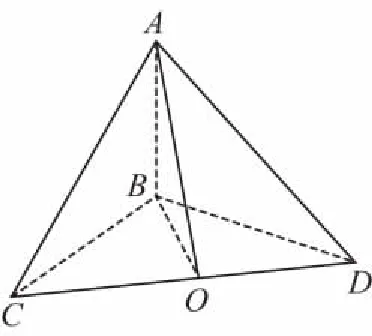
【评注】一个三棱锥中存在两个直角三角形,先确定这两个直角是否有共同的斜边.如果这两个直角三角形有共同的斜边,那么问题就简单了,外接球的球心就在斜边的中点上.根据题目给定条件求出两直角三角形的斜边长度,外接球半径就是它的一半.

五、投影法

球心与截面小圆的圆心连线与截面垂直，因此，如果两条线在两个截面中的投影分别为两个截面小圆的圆心，那么这两条线的交点就是球心，这种确定外接球球心的方法为投影法.

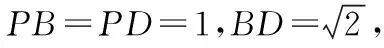
设该四面体内切球的半径为r，

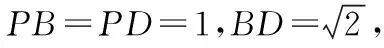
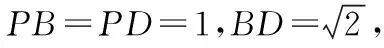
解法4(性质法)：由于平面PBD⊥平面BCD，平面PBD∩平面BCD=BD，CD⊥BD，则CD⊥平面BPD，由于BP⊂平面PBD，则CD⊥BP，由于PD⊥BP,PD∩CD=D,则BP⊥平面PCD，又由于PC⊂平面PCD，则BP⊥PC.由于△PBC，△DBC是以BC为共同斜边的直角三角形，则可以采用性质法求解.如图所示，取BC边的中点O，在Rt△PBC中，OP=OB=OC，在Rt△DBC中，OD=OB=OC，故O为四面体外接球的球心.后续求解过程同上.