解读匀变速曲线运动的分析策略

福建 郑行军

匀变速曲线运动作为中学物理的一个考点往往以具体的运动模型呈现，如平抛运动、带电粒子在电场中的偏转等，因此使得教师在讲解或是学生在复习的过程中也常常局限于以上几类较简单的问题，而对于运动的拓展和延伸分析难以形成清晰思路。近年来高考物理命题设计的总体思路往往是在教材资源的基础上通过转化、改编和迁移，推陈出新，考查学生的学习能力。匀变速曲线运动作为匀变速运动和曲线运动两类基本运动形式的结合体，在中学物理运动模型中具有特殊的地位，作为典型的运动模型，匀变速曲线运动的分析体现出与匀变速直线运动和圆周运动不同但又关联的解题思路，因此在高考中是一个热度较高的高频考点。这就要求学生不仅能分析典型直观的运动模型，还要拓展至一般的匀变速曲线运动问题，因此在高考最后冲刺阶段，做好回顾、反思、总结和预测就显得很有必要，本文就匀变速曲线运动的几个知识要点进行归类讲解，希望对冲刺阶段的备考有所帮助。

一、题型界定

1.模型定义：匀变速曲线运动是指在运动过程中，加速度方向与速度方向不共线且加速度恒定(即加速度大小不变，方向也不变)的运动。

2.运动性质(题型)判定：

(1)加速度始终为恒量(即合力为恒力)；

(2)初速度不为零且合力方向(即加速度方向)与速度方向不共线，即运动轨迹为曲线。

二、可行性方法策略探析

1.合成与分解法：将曲线运动正交分解为两个相互垂直的简单的直线运动，根据分解后的分加速度和分速度判断分运动的性质，由牛顿运动定律和运动学公式求出分速度和分位移，再利用运动的合成求出与合运动相关的物理量。其中用正交分解法分解矢量和分运动的性质判断是解题的两个重要环节。

【知识拓展】正交分解法的建轴标准：

(1)应使尽可能多的矢量(如力和速度)与坐标轴重合。

(2)若初速度方向与合力方向垂直，可以分别沿着初速度方向和合力方向建立直角坐标系。

(3)若采用不同的坐标轴分解的矢量(如力和速度)相同，应尽量不分解力。

2.动能定理、动量定理或功能关系法：对物体受力分析，运用动能定理或动量定理求解，此方法主要讨论物体的合运动参量，如合位移、合速度等，动能定理可分析速度与位移的关系，动量定理可分析速度与时间的关系。

三、典例剖析

【例1】一物体质量为m，在光滑的水平面上以速度v0沿AB方向匀速运动，在某一时刻(位置O处)受到两个互相垂直的水平恒力作用，一个力大小为F，另一个力的方向与v0的方向成θ角，如图1所示，当物体速度为2v0时，物体正处于另一个力的作用线OP上的P点，求：

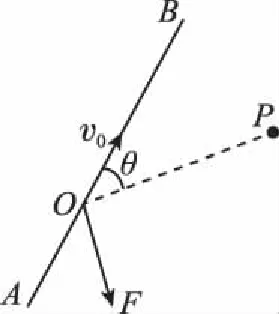
图1

(1)物体从O到P的运动时间t；

(2)物体从O到P的位移x；

(3)OP方向上的作用力F1。

【解析】(1)对物体受力分析，物体在水平面上做匀变速曲线运动，由建轴标准中的(1)，以OF为y轴，OP为x轴，O为原点建立坐标系如图2所示，由运动的合成与分解得：

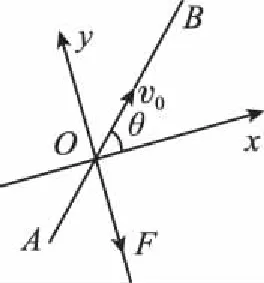
图2

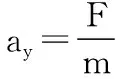
x方向的初速度：v0x=v0cosθ

从O到P的时间内y方向的位移为零：

(2)在P点x方向的速度和y方向的初速度等大反向，故x方向的速度：

从O到P的位移：

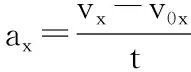
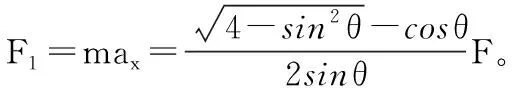
【点评】本题考查了匀变速曲线运动的研究方法——运动的合成与分解，受力分析后建立坐标系分解成两个分运动，运用牛顿运动定律和运动学公式研究分运动的规律，联立求解。

( )

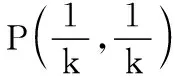
图3

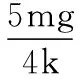
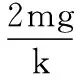
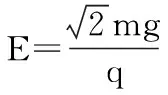
【答案】CD

【点评】本题结合了匀变速曲线运动和匀强电场的性质两个知识点，是高考常见的一种命题形式——组合题型。解题思路由轨迹方程入手可确定小球的运动性质及合力方向，根据运动的合成与分解得出小球分运动性质，再由分运动列方程求出小球运动的初速度、末速度及加速度，进而解出电场强度大小、动能和其他物理量。

【例3】在竖直平面内存在着互相垂直的水平匀强电场和水平匀强磁场，电场强度为E，磁感应强度为B。该场中有一长为L的绝缘硬直板AC，与水平方向成θ角，如图4所示。质量为m、电荷量为q的带电物块(可视为质点)，从板的A端由静止开始下滑，到达C端时物块对板面恰无压力，物块与板之间的动摩擦因数为μ。物块离开直板后运动到D点时速度达到最大值，同时撤去磁场，物块能继续运动到D点正下方高度差为h的P点，(重力加速度为g)求：

图4

(1)物块运动过C端时的速度大小；

(2)物块从A到C过程中克服摩擦力做的功；

(3)物块从D点运动到P点的时间t。

【解析】(1)小物块刚到达C端时，受力分析如图5，由于恰好无压力，有：

qvCB=mgcosθ+qEsinθ

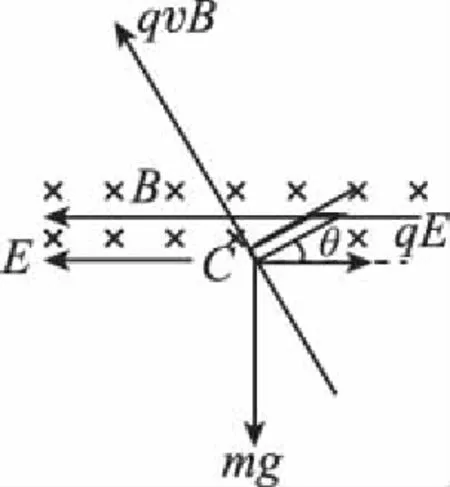
图5

(2)物块从A到C过程由动能定理有：

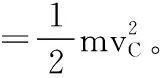
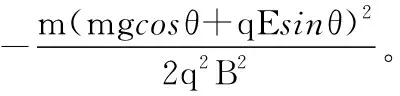
(3)物块速度最大时，速度方向与电场力、重力的合力方向垂直，撤去磁场后物块做匀变速曲线运动，根据建轴标准中的(2)分别沿重力和电场力的合力方向(y轴)和垂直于合力方向(x轴)建立直角坐标系，由运动的合成与分解得

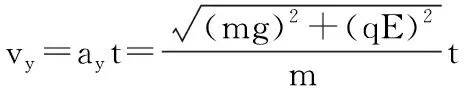
由于DP与电场线垂直，即DP是等势线，故从D到P过程电场力做功为0，设物块到达D点的速度大小为vD，由动能定理：

根据运动的合成与分解知P点的速度大小为：

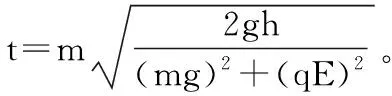
【点评】本题综合了电磁场的叠加场问题和匀变速曲线运动问题，解决关键是分析清楚物块的运动过程，合理的建立直角坐标系，运用运动的合成与分解逐步求解。

【例4】如图6，平行板电容器两极板的间距为d，极板与水平面成45°角，上极板带正电。一电荷量为q(q>0)的粒子在电容器中靠近下极板处，以初动能Ek0竖直向上射出。不计重力，极板尺寸足够大。若粒子能打到上极板，则两极板间电场强度的最大值为

( )

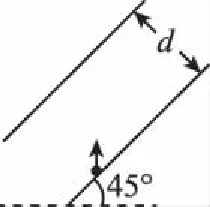
图6

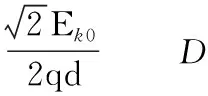
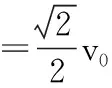
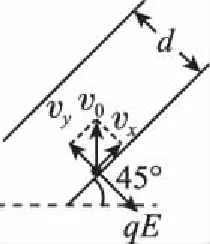
图7

【答案】B

【点评】粒子只受到电场力的作用，只有电场力做功，当粒子恰好到达上极板时速度恰好与上极板平行，根据粒子运动的性质将曲线运动分解为垂直极板和平行极板的两个分运动，再结合运动学公式求解。本题关键是明确粒子的受力情况和运动情况，然后根据匀变速曲线运动的规律和合理的建轴分解计算电场强度的大小。

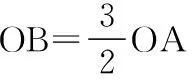
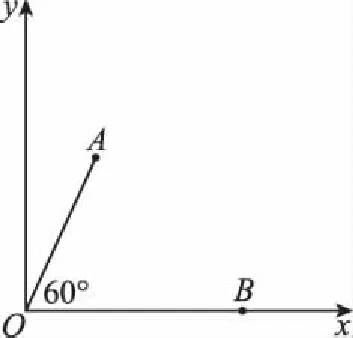
图8

(1)第一次运动经过A点时的动能与初动能的比值；

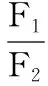
dsin60°=v0t

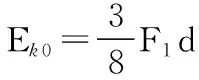
小球到达A点时水平方向的速度大小为：

则小球到达A点的动能为：

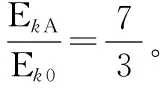
(2)施加恒力F2后，小球从O点到A点和B点，由动能定理得知：

运动到A点时有：

运动到B点时有：

设F2与x轴的夹角为α，则由功的公式得：

解得α=30°

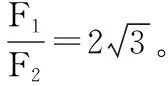
【点评】只有恒力F1时，滑块做匀变速曲线运动，根据运动的合成与分解和牛顿第二定律，加了恒力F2后，由功能关系列方程，再结合恒力做功的特点进行解答。本题的关键要掌握匀变速曲线运动的研究方法——运动的合成与分解，运用牛顿运动定律和运动学公式研究分运动的规律，结合功能关系研究问题。

综上所述，在运用运动的合成与分解分析匀变速曲线运动时，正交分解法建轴分解是一个非常重要的环节，科学合理的直角坐标系，会大大的简化解题过程，提高解题效率，因此在解题过程中要仔细分析题设条件呈现的物理情境，挖掘问题情境的内在规律，找出其共有本性，规范解题思路，从而收到事半功倍的效果。