不同的考生 相同的错误——几个临界问题拾零

重庆 杨天才(特级教师，研究员)

时隔几年后，关于临界问题，高考又出现了同类型的题目，但众多学生还是犯了相同的错误，如物体的速度为零，一定处于平衡状态；物体在最高点，速度一定为零；物体速度最大，加速度一定为零等。正确的观点如下表。

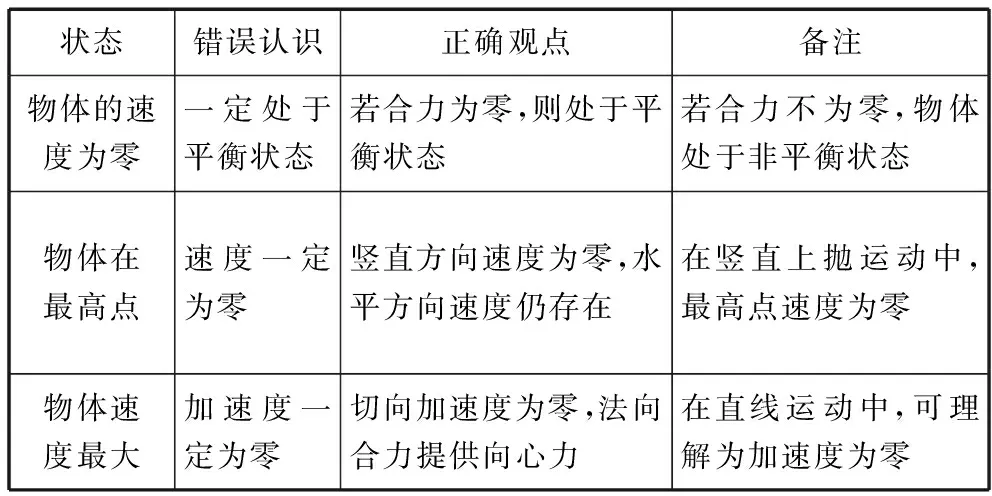
状态错误认识正确观点备注物体的速度为零一定处于平衡状态若合力为零,则处于平衡状态若合力不为零,物体处于非平衡状态物体在最高点速度一定为零竖直方向速度为零,水平方向速度仍存在在竖直上抛运动中,最高点速度为零物体速度最大加速度一定为零切向加速度为零,法向合力提供向心力在直线运动中,可理解为加速度为零

【例1】(1997·全国卷第24题)在方向水平的匀强电场中，一不可伸长的不导电细线的一端连着一个质量为m的带电小球，另一端固定于O点。把小球拉起直至细线与场强平行，然后无初速释放。已知小球摆到最低点的另一侧，线与竖直方向的最大夹角为θ(如图1所示)。求小球经过

最低点时细线对小球的拉力。

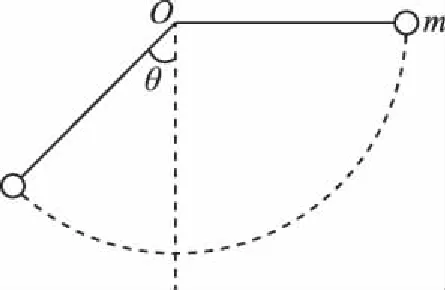
图1

【错解】线与竖直方向的最大夹角为θ，即小球的速度为零，小球处于平衡状态，对小球受力分析，由力的平衡条件得：qE=mgtanθ。

【分析】小球的速度为零时，未处于平衡状态，而是立即掉头进行往复运动(类似单摆的最高点)，由动能定理知：mglcosθ-qEl(1+sinθ)=0成立。

【解析】设细线长为l，球的电量为q，场强为E。若电量q为正，则场强方向在图1中向右，反之向左。从释放点到左侧最高点，重力势能的减少量等于电势能的增加量，有：

mglcosθ=qEl(1+sinθ)

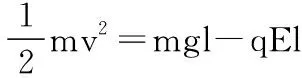
【例2】(2005·全国卷Ⅰ第24题)如图2所示，质量为m1的物体A经一轻质弹簧与下方地面上的质量为m2的物体B相连，弹簧的劲度系数为k，A、B都处于静止状态。一条不可伸长的轻绳绕过轻滑轮，一端连物体A，另一端连一轻挂钩。开始时各段绳都处于伸直状态，A上方的一段沿竖直方向。现在挂钩上挂一质量为m3的物体C并从静止状态释放，已知它恰好能使B离开地面但不继续上升。若将C换成另一个质量为(m1+m3)的物体D，仍从上述初始位置由静止状态释放，则这次B刚离地时D的速度的大小是多少(已知重力加速度为g)。

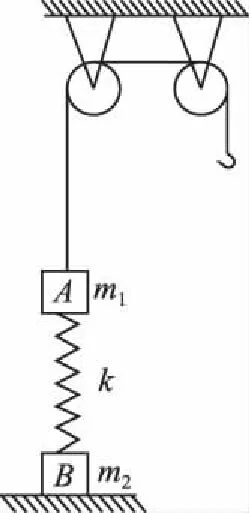
图2

【错解】挂钩上挂一质量为m3的物体C并从静止状态释放，它恰好能使B离开地面但不继续上升。说明此时C的速度为零，C也处于平衡状态，有：(m1+m2)g=m3g。

【分析】其实C的速度为零时并未处于平衡状态，(m1+m2)g=m3g不成立，从挂上物体C到其最低点，根据机械能守恒定律有：ΔE弹=m3gh-m1gh成立。

【解析】开始时，B静止平衡，设弹簧的压缩量为x1，有：kx1=m1g，挂C并释放后，C向下运动，A向上运动，当B刚要离开地面时，设弹簧伸长量为x2，有：kx2=m2g。此时，A和C速度均为零。从挂C到其最低点，根据机械能守恒定律，弹簧弹性势能的改变量为：

ΔE=m3g(x1+x2)-m1g(x1+x2)

将C换成D后，有：

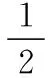
【例3】(2016·全国卷Ⅱ第25题)轻质弹簧原长为2l，将弹簧竖直放置在地面上，在其顶端将一质量为5m的物体由静止释放，当弹簧被压缩到最短时，弹簧长度为l，现将该弹簧水平放置，一端固定在A点，另一端与物块P接触但不连接。AB是长度为5l的水平轨道，B端与半径l的光滑半圆轨道BCD相切，半圆的直径BD竖直，如图3所示，物块P与AB间的动摩擦因数μ=0.5。用外力推动物块P，将弹簧压缩至长度l，然后放开，P开始沿轨道运动，重力加速度大小为g。若P的质量为m，求P到达B点时的速度的大小，以及它离开圆轨道后落回到AB上的位置与B点之间的距离。

图3

【错解】当弹簧被压缩到最短时，质量为5m的物体处于平衡状态，由力的平衡条件，有：5mg=kl

【分析】当弹簧被压缩到最短时，弹簧两端物体的速度相等，物体速度为零。但不满足平衡状态，此过程用能量守恒得：5mgl=Ep。

【解析】弹簧在地面上有重力势能转化为弹性势能，即5mgl=Ep，此时弹簧长度为l，A→B由能量守恒有：

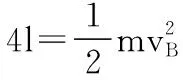
B→D由动能定理有：

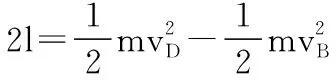
此后物体做平抛运动，满足：

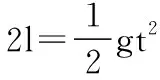
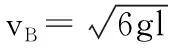
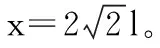
【例4】(2015·福建卷第22题)如图4所示，绝缘粗糙的竖直平面MN左侧同时存在相互垂直的匀强电场和匀强磁场，电场方向水平向右，电场强度大小为E，磁场方向垂直纸面向外，磁感应强度大小为B。一质量为m、电荷量为q的带正电的小滑块从A点由静止开始沿MN下滑，到达C点时离开MN做曲线运动。A、C两点间距离为h，重力加速度为g。

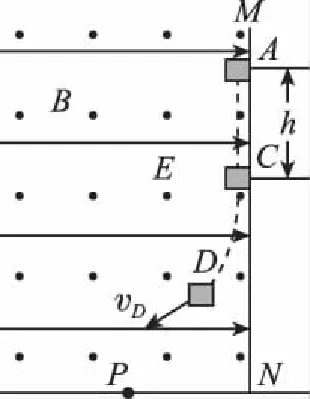
图4

(1)求小滑块运动到C点时的速度大小vC；

(2)求小滑块从A点运动到C点过程中克服摩擦力做的功Wf；

(3)若D点为小滑块在电场力、洛伦兹力及重力作用下运动过程中速度最大的位置，当小滑块运动到D点时撤去磁场，此后小滑块继续运动到水平地面上的P点。已知小滑块在D点时的速度大小为vD，从D点运动到P点的时间为t，求小滑块运动到P点时速度的大小vP。

【解析】(1)小滑块沿MN运动的过程中，水平方向受力满足：

qvB+N=qE

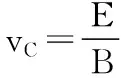
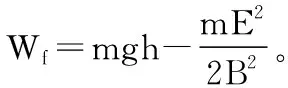
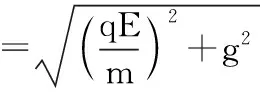
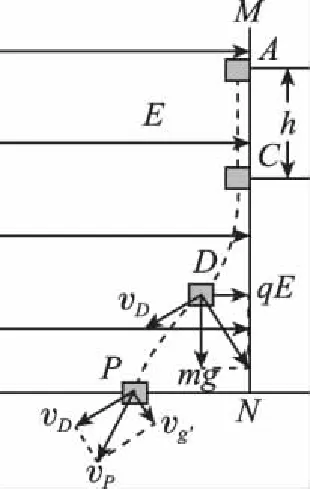
图5

【点评】第(3)问学生得分率较低，学生误以为速度最大的位置加速度为零，得出洛伦兹力与电场力、重力的合力相等的结论，其实，此时滑块做曲线运动，切向加速度为零，径向合力提供向心力。

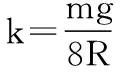
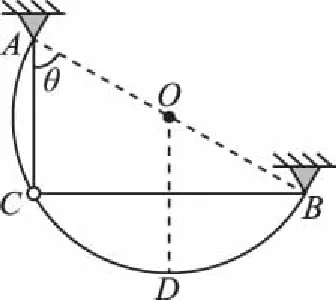
图6

(1)如果导轨是光滑的，求圆环到达D点时，弹性轻绳的弹力F的大小以及圆环到达D点时的速度v的大小；

(2)如果导轨是粗糙的，且圆环与导轨间的动摩擦因数为μ，已知圆环运动到D点时恰好达到最大速度，求圆环由C点运动到D点过程中克服摩擦力做的功Wf。

【解析】(1)在D点处弹性轻绳的伸长量为：

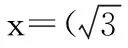
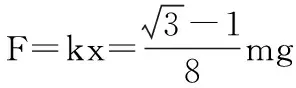
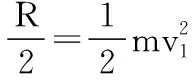
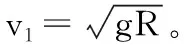
(2)圆环在D处速度最大，即切向合力为零，由μN+F·cos60°=F·sin60°得：

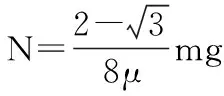
法向方向，由牛顿第二定律有：

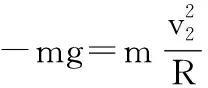
圆环由C到D由动能定理有：

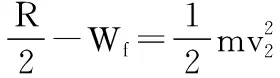
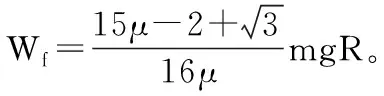
【点评】与上题类似，学生误以为圆环运动到D点时恰好达最大速度，加速度为零，得出错误结论。其实，此时滑块做变速圆周运动，径向合力仍然提供向心力，而切向加速度为零。