混合苍狼优化算法在全局最优中的应用研究
张小青,张玉叶,郝海燕
1.咸阳师范学院 物理与电子工程学院,陕西 咸阳 712000
2.西安电子科技大学 机电工程学院,西安 710071
1 引言
随着计算机的发展,各种智能控制器也应运而生,模仿生物群体功能的智能优化控制器越来越受到众多学者与科研人员的关注。目前较为典型的智能控制器的算法有遗传算法[1]、粒子群算法[2]、蚁群算法[3]、蜂群算法[4]、鱼群算法[5]等,在近几年又提出了一种苍狼优化算法(Grey Wolf Optimizer,GWO)。苍狼主要产于欧洲与北美,是一种较具战斗力的狼。苍狼猎食常是一种聚群行为,狼群里各个个体通过相互沟通与合作,常常能将体型远远大于其自身体型的猎物捕获。正是受苍狼群体捕猎的启发,2014年苍狼优化算法被提了出来[6]。
苍狼优化算法一方面由于其简单、通用性强,在理论和工程上都得到了一定的青睐,很快使其在各行各业的工程上得到了较好应用,主要包括电力系统领域及其相关的参数优化控制[7-10]、永磁同步电动机混沌控制[11]、多层感知器的训练[12]、表面波参数估计[13]、光普波段寻优选择[14]等。但另一方面由于其本身存在探索深度浅,开发能力差且易限于局部最优等缺点,又使得该算法在实际应用中受限。文献[15]针对苍狼算法进行了改进,提出了一种针对搜索狼中较差的个体进行重新定位的改进苍狼优化算法(GWO-EPD),在一定程度上提高了原算法的开发与探索能力,但从算法的实验验证结果中发现其搜索效果依然不太令人满意,因此为了更好地提升GWO性能,提出了一种新的混合改进的苍狼优化算法,结合自主搜索、差狼淘汰重组及优秀狼差分变异的思想构成了混合苍狼优化算法(MAR-GWO)。
2 算子分析
在GWO算法[6]中,苍狼分为四个等级,最高等级为alfa(α)狼,第二等级为beta(β)狼,第三等级为delta(δ)狼,此为三领导层狼,最后一等级为搜索狼即omega(ω)狼。α、β及δ狼一般在数量上仅设一只,而ω狼可设为几十只[16]。GWO算法关键在于ω狼的搜索行为,ω狼的搜索算法描述如下:
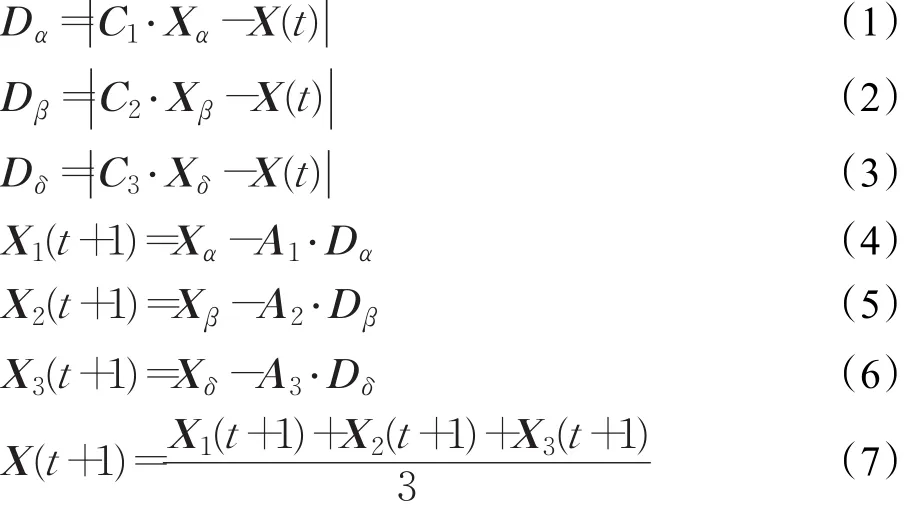
上面公式隐含着搜索狼仅在α、β及δ狼附近进行猎物抓捕行动,其中Xα、Xβ、Xδ分别是α、β与δ狼当前所在的位置矢量,X(t)是当前ω狼所在的位置矢量,X(t+1)是更新后的ω狼所在的位置矢量,C1、C2、C3分别是围绕α、β及δ狼搜索时的权值,C值小,在对应的领导层苍狼周围小范围内执行搜索,C越大,则在对应领导层苍狼周围越大范围内执行搜索。D用来计算ω狼到α、β及δ三领导层狼之间的距离,又用A来体现相应距离D的权重。A相应取值范围为[-1,1],A与C 的通用计算 A=2a·r1-a,C=2·r2,r1、r2是[0,1]范围内的随机向量,a中的元素是随迭代次数从2递减到0的数。
在标准苍狼优化算法中,ω狼仅在α、β及δ狼的基础上进行搜索,一旦α、β及δ狼全部处于某一局部最优附近的可行域时,算法较容易陷入局部最优,而且算法中α、β及δ只有当搜索狼的性能优越时才会被动地更新,这使得算法总体的开发与探索能力都不是很强。新的混合算法在GWO算法的基础上吸收进α、β及δ狼的自主搜索、性能较差的搜索狼淘汰重组机制及部分优秀搜索狼按概率变异等算子,以提升算法的开发与探索能力。这里所说的性能好坏是依据苍狼位置矢量求出来的性能值的好坏来衡量的,例如在求最小值问题中,如果某苍狼位置矢量代入问题中求得的解值越小,即认为其性能值越小,则该苍狼性能越优越。
2.1 自主搜索算子
自主搜索算子又被称为主动捕猎(Preying initiatively)[16]算子,指狩猎者在其可视范围内自主进行捕猎,其计算算子为:

式中x(i)是当前狩猎者的第i维状态的位置值,等号右边的第二部分可以认为是自主搜索的步长,其中λ是捕猎速度,r为可视范围,rand()为[-1,1]间的随机数。此算子又可以理解为在狩猎者周围一个大小为λ×r的圆域范围内进行随机自主搜索,其中可视范围r是一定值,与变量搜索范围有关。为了更好地体现变量搜索范围(xmax,xmin)与搜索步长的关系,将自主搜索算子式(8)改为:

式(8)中的rand()项用式(9)中的正弦项替代,表示每只苍狼在其周围h个方向进行自由搜索,式(9)中xid为第i只苍狼的第d维状态的位置值,为xid在第p个方向自主搜索后的位置值,其中 p=1,2,…,h,xmax、xmin分别为d维状态变量的最大、最小取值,λ为搜索速度,通常可取为1,τ为步长因子。τ越大表示搜索越细密,精度越高,但计算量也会越大,搜索效果进展可能会越慢,所以一般自主搜索需要权衡τ的取值。
2.2 淘汰重组算子
对性能较差的搜索狼提出淘汰重组机制,目的是优化搜索资源,提高搜索效率[17]。重组算子如下:
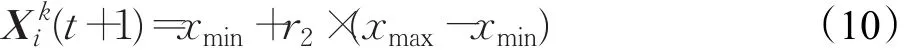
2.3 优秀搜索狼变异算子
优秀搜索狼的变异行为算子的引入是为了进一步全面扩展算法的搜索域,采用按概率进行的差分进化变异,算法如下:
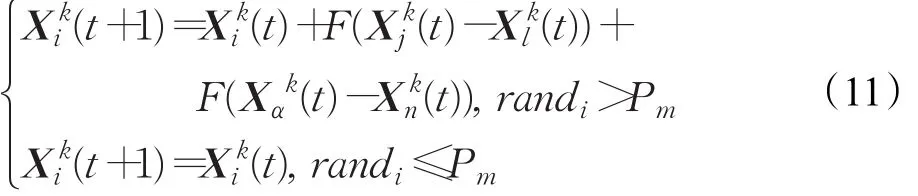
3 混合苍狼优化算法的设计
结合以上所述,给出混合苍狼优化算法的结构如下:
步骤1初始化。
(1)随机在搜索空间中产生alfa(α)、beta(β)、delta(δ)及omega(ω)群体。
(2)计算α_score、β_score、δ_score初始性能值。
(3)初始化自主捕猎方向数h、步长因子τ、变异概率Pm等相关参数。
(4)G=l%迭代次数计数
步骤2越界判断与处理。
步骤3根据具体的问题,求取各omega(ω)苍狼的性能值。
If omega(ω)性能优于alfa(α)、beta(β)或delta(δ)
omega(ω)替换alfa(α)、beta(β)或delta(δ)
else alfa(α)、beta(β)或 delta(δ)保持不变 end
步骤4 自主捕猎阶段:alfa(α)、beta(β)、delta(δ)采用式(9)进行自主捕猎行为。
步骤5按式(1)至式(7)更新omega搜索狼的位置。
步骤6优秀狼差分变异阶段。
(1)对性能优良的R_num只搜索狼按公式(11)进行差分变异
(2)贪婪选择:If变异后的搜索狼优于父代搜索狼
变异后代被保存else变异失败 end
步骤7淘汰重组阶段:对性能较差的搜索狼按式(10)进行淘汰重组操作。
步骤8 IfG≥Gmax
结束运行并输出最优解和最优个体
else转至步骤2 end
4 仿真实验
在这一章中把混合苍狼优化算法(MAR-GWO)应用到13个标准全局最优问题中,第一组为表1所示单峰寻优问题;第二组为表2所示多峰寻优问题。把MARGWO分别与GWO算法、GWO-EPD算法、粒子群算法(PSO)及进化算法(EA)进行比较,最大迭代次数均为500次,每个实验重复30次。所有实验中各算法的参数取值均一致,如表3所示。
4.1 单峰问题寻优分析
表4为单峰函数的数值寻优结果,表中AVE为30次重复实验得到的平均寻优值,STD为标准偏差,BEST为重复实验中的最佳寻优值,WORST为最差寻优值,多峰问题寻优结果的符号表述与此相同。在实验过程发现从 f1~f4,MAR-GWO算法均能100%找到其理论最优值0,这相对于其他算法来说其寻优能力占有明显的优势。虽然 f5和 f6的结果在所对比的算法中不是最优的,但其实验结果明显优于标准的GWO算法。图1给出了GWO、MAR-GWO、GWO-EPD、PSO及EA五种算法在单峰函数寻优迭代过程中最优轨迹图。从轨迹图来看,对于 f1~f4的结果图来说,始终未见MAR-GWO的轨迹曲线,这是由于MAR-GWO在 f1~f4中的寻优过程中收敛过快引起的。由于其收敛速度非常快,以至于在横坐标为500时迭代次数过小而不容易显示清楚,放大后的轨迹图如图2所示。从图2看,f1~f4基本在第2次迭代就已得到了理论最优值0,这充分说明了混合苍狼优化算法MAR-GWO具有很强的寻优能力。需说明的是图1的纵坐标为以10为底的对数坐标,横坐标为线性坐标。
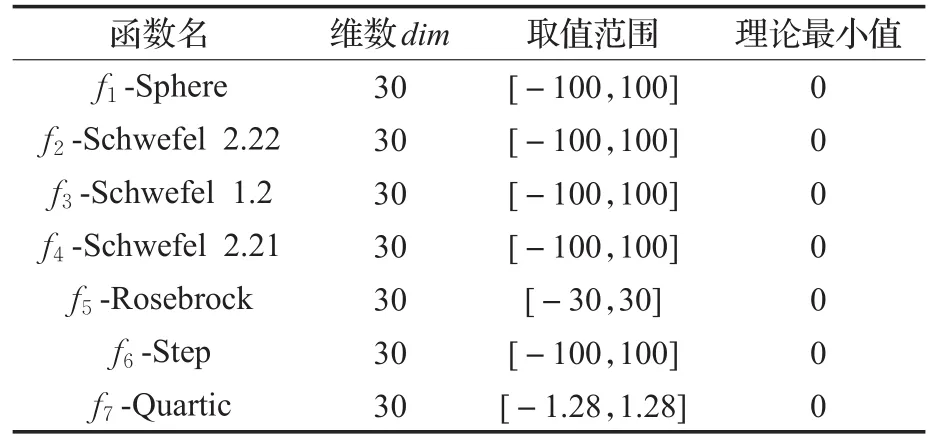
表1 单峰标准函数
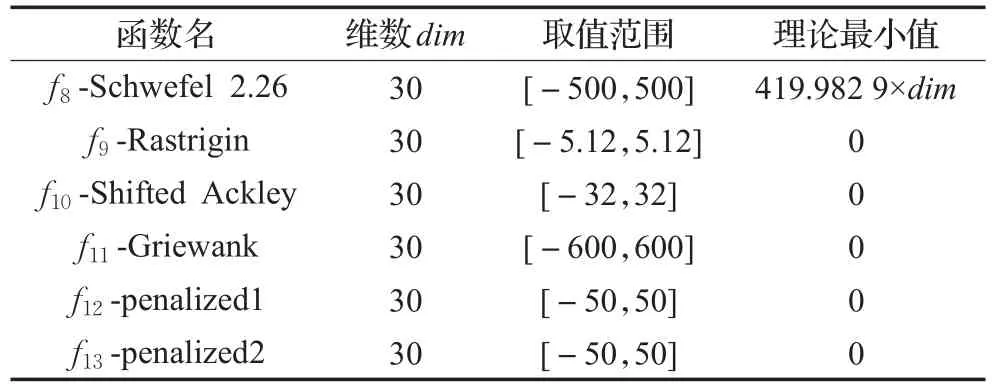
表2 多峰标准函数

表3 算法参数取值说明
4.2 多峰问题寻优分析
表2中各函数维数都为30维,难点在于避免进入局部最优。表5为多峰函数寻优数值结果,对于 f8~f11,MAR-GWO算法寻优结果具有较明显的优势,尤其对于f9~f11,在实验中MAR-GWO基本是100%能寻到其理论最佳值0,这一点通过寻优轨迹图(图3)也可看出。在图3中,f9~f11的轨迹曲线中又不见MAR-GWO的曲线,这与前面一样,说明该算法在此函数寻优过程中收敛相当快,稳定性好。虽然在 f12~f13的寻优中,MARGWO不是最优,但其寻优结果显然都要优于标准
GWO,这在一定程度上说明MAR-GWO改进的方向是正确的。另外,对于 f8与 f10的MAR-GWO寻优轨迹基本都在左下角与坐标轴重叠处,这也意味着算法收敛速度很快。
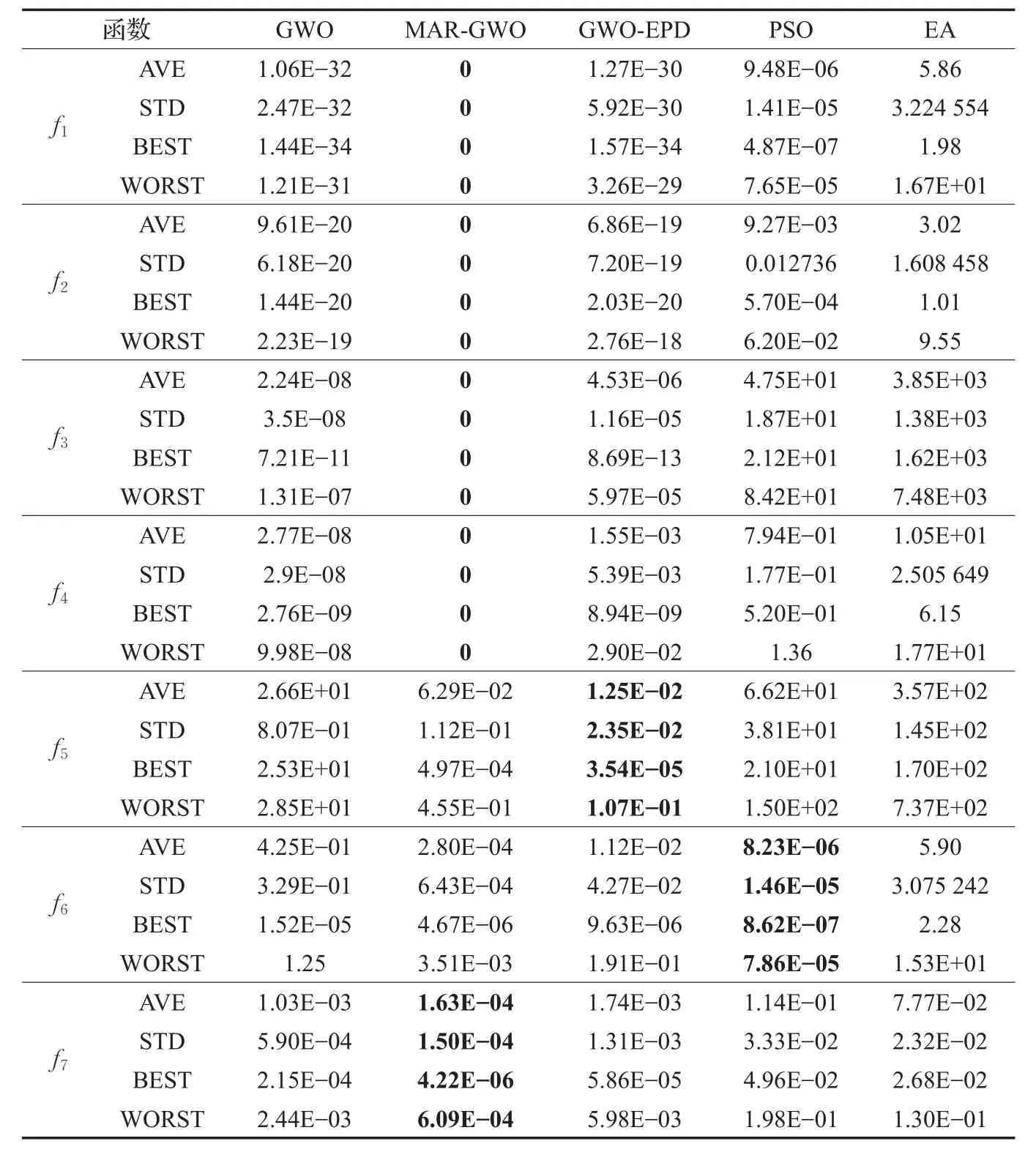
表4 单峰寻优结果
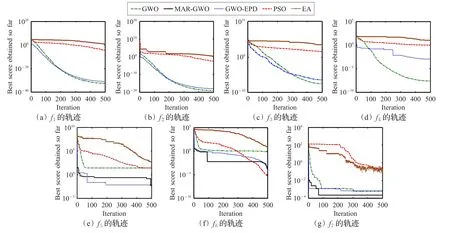
图1 单峰标准函数寻优实验迭代轨迹图

图2 f1~f4放大后的迭代轨迹图(MAR-GWO)

表5 多峰函数寻优结果

图3 多峰标准函数寻优实验迭代轨迹图
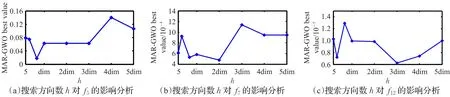
图4 搜索方向数h对控制算法的影响分析
5 参数对控制算法的影响
本章只研究自主捕猎中的两个比较重要的参数(步长因子τ与搜索方向数h)对控制算法性能的影响。
5.1 步长因子τ对控制算法的性能影响
把步长因子设定在2 000到20 000之间,以间隔2 000为步长进行测试,在每个步长确定的情况下进行30次重复试验,记录4个函数的平均值,共测试得到10个数据点,列表如表6。
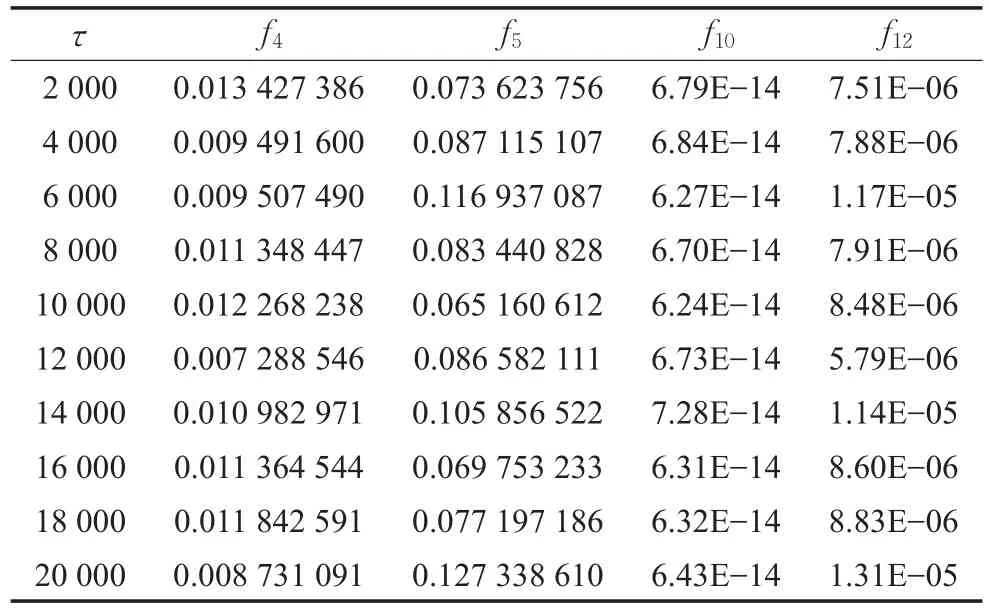
表6 步长因子τ的影响分析
如果不考虑计算机的计算能力有限,理论上增加步长,即可增加算法的开发深度,但事实上,从实验所得的数据来分析,步长τ增加的过程中,其最优平均值的变化并不是按照单一的方向进行增加或减少,而是在迂回振荡,不同的问题由于变量取值范围不同,最佳的步长因子τ也不一样。经分析 f4与 f12的最佳步长因子τ大约为12 000,而 f5与 f10的最佳步长因子τ大约为10 000。
5.2 搜索方向数h对控制算法的性能影响
一般,h对算法的影响规律:h越小开发能力越强,但其探索能力相应减弱;h越大则算法的开发能力变弱但其探索能力会相应地加强。所以在调试算法参数时需选择合适的h值。图4以 f5、f7、f12为例,通过改变搜索方向数h来研究MAR-GWO优化算法的性能。f5、f7为单峰函数,f12为多峰函数,从大体上来看h对单峰函数的性能影响规律更明显些,从图4大致可以得知,f5的最佳h约在20附近,f7可以近似认为h最佳值在20~2 dim附近,但 f12则似乎不只显示一个最佳值,在h为10 dim与3 dim处出现了明显的相差不远的谷值,这可以归为算法在多峰问题中开发与探索能力两方面的均衡结果。
6 总结
考虑到提高算法开发与探索能力,针对标准GWO算法,引入了α、β、δ领导层苍狼的自主捕猎算子、对性能较差苍狼的淘汰重组机制及优秀苍狼按概率变异算子,最终提出了一种混合苍狼优化算法,即MAR-GWO算法。以高维13个标准函数作为寻优对象,并把改进的GWO算法(GWO-EPD)、PSO算法、EA算法等作为比较算法,分别进行了数值寻优实验。相比于标准GWO算法,MAR-GWO寻优效果均优越得多,提高了算法克服局部最优的能力。另外,从各函数轨迹图来看,MAR-GWO收敛速度要较标准GWO快得多。与改进后的算法GWO-EPD的结果相比,优势也很明显,MARGWO具有很强的竞争力。
步长因子τ与搜索方向数h对控制算法的性能有一定的影响,对于性能要求不是太高的场合,一般取τ=2 000~6 000,h=20~50之间的某定值可满足要求,否则需具体问题具体确定其参数值。

