基于离散萤火虫算法的指控结构适应性调整

陈冠宇，孙 鹏，2，张杰勇，武君胜

1.空军工程大学 信息与导航学院，西安 710077

2.西北工业大学 计算机学院，西安 710077

3.西北工业大学 软件与微电子学院，西安 710077

1 引言

指挥控制（Command and Control，C2）组织是围绕特定的作战目标，由各作战单元紧密联系而形成的作战整体。组织权变理论认为，“没有普遍适用的组织模式，只有在具体使命环境下，适用于具体条件的最佳组织[1]。”面对复杂多变的战场环境，指控组织应当具有敏捷性，即指控组织能够根据战场环境的变化进行适应性调整[2]。

指挥控制结构是指控组织中的关键要素，合理的指挥控制结构能够提高组织的作战效率[3]。作战使命执行过程中，可能会出现平台损毁、任务新增、行动计划改变以及决策实体失效等突发情况[4]。若不相应地调整指控组织结构，仍保持突发事件出现前的指挥控制组织结构，则指控组织的作战效能将大大降低。因此，指控组织需要适应性地调整指控结构以应对突发事件对作战效能的影响。

当前对指控组织结构适应性调整问题的研究，已经取得不少成果，文献[2]考虑了响应时间、平均备份数和负载均衡等参数，采用着色Petri网研究组织结构的适应性调整；Levchuk等人提出了基于三阶段思想的指控结构调整方法，对调整代价和调整后的性能进行权衡来选择结构的调整路径[5]；杨春辉等结合着色Petri网和遗传算法进行了C2组织适应性优化研究[6]；文献[4]提出了基于粒度计算的组织结构适应性设计方法；牟亮等人[7]提出了基于滚动时域的C2组织动态适应性优化方法，提高了指控结构动态调整的性能。

从当前的研究来看，关于指控结构调整的研究上还有些问题亟待解决。在考虑突发事件上，较少考虑决策实体失效的情况，多以行动计划改变为主；在指控结构的性能测度上，缺少考虑变化前组织的状态对性能的影响；在调整算法方面，算法的实时性还可以进一步提高，以满足变化较快的战场环境。

针对这些问题，本文给出了指控结构性能测度方法，针对行动计划改变和决策实体失效这两类突发情形，分别建立指控结构适应性调整模型，并提出了一种基于离散萤火虫算法的求解方法。最后通过案例仿真验证该算法的有效性。

2 指挥控制组织的实体

指挥控制组织内有三类实体，分别是任务实体（Task，T）、平台实体（Platform，P）和决策实体（Decision-Maker，DM）[4]。这三类实体是C2组织的组成元素。

（1）任务实体（Task，T）：是由作战使命分解得到的作战活动，任务的完成需要相关的决策实体指挥控制特定的平台实体对任务进行处理。组织中所有任务实体的集合，记为ST={T1,T2,…,TNT}，NT为组织中任务实体的总数。

（2）平台实体（Platform，P）：为执行任务提供作战资源，是直接执行和完成作战任务的实体。组织中平台实体的集合，记为SP={P1,P2,…,PNP}，NP为组织中平台实体的数量。

（3）决策实体（Decision-makers，DM）：是组织中实施指挥控制、协作交流和管理平台活动的实体，负责指挥相关平台实体处理对应的任务。

根据决策实体的职责，决策实体可分为控制全局层面的战役决策实体（Operational Decision-Maker，ODM）和控制平台执行具体的作战任务的战术决策实体（Tactical Decision-Maker，TDM）。C2组织中存在多个战术决策实体，但只有一个战役决策实体。

组织中战术决策实体的集合，记为STDM={TDM1,TDM2,…,TDMND}，ND为战术决策实体的总数。

3 指挥控制组织结构适应性调整问题建模

3.1 关系变量定义

指控组织结构分为决策层、任务层和平台层，在这三层面中，同类以及不同种类实体间具有不同的关系，实体间的各种关系，共同构成了兵力组织的结构[8]，如图1所示。

图1 指挥控制组织结构

对C2组织中的各种关系进行如下定义：

（1）战术决策实体对平台实体的指控关系RTDM-P

RTDM-P由矩 阵 MTDM-P=()ND×NP表 示 ，决策实体TDMi与平台Pj的配置变量。MTDM-P也称为决策实体配置方案。

（2）战术决策实体间的协作关系RTDM-TDM

RTDM-TDM可由矩阵=()ND×ND表示，代表决策实体TDMi与TDMj间的协作变量。

（3）平台实体对任务实体的分配、处理关系RT-P

RT-P可由矩阵MT-P=()NT×NP表示，代表平台实体Pj与任务实体Ti的分配变量。

（4）战术决策实体对任务实体的执行关系RTDM-T

RTDM-T由矩阵 MTDM-T=()ND×NT表示，表示战术决策实体TDMi与任务Tj执行关系。

当MT-P和MTDM-P确定后，MTDM-T=()ND×NT可由下式确定：

（5）任务间的时序关系RT-T

RT-T可由矩阵 MT-T=()NT×NT表示，表示任务的时间关系。

3.2 指挥控制组织结构的优化目标

对于确知的任务计划，设计同任务计划匹配程度较高的指控组织结构，可使组织内每个战术决策实体承担的任务较为均衡，有效地减少了战术决策实体间的交流与协作，降低了决策实体的工作负载。因此，可用指控组织内战术决策实体的负载水平来衡量指控组织结构的性能。

3.2.1 工作负载的定义

战术决策实体的工作负载，反映了决策实体在执行作战任务的过程中指挥控制平台实体的情况。考虑到在作战进行过程中单个战术决策实体，除了对自身负责的平台实体进行指挥控制而产生负载；也会与其他战术决策实体进行局部协作，因此产生部分工作负载。因此，在定义工作负载时，既要考虑指控负载，也要考虑协作负载。即工作负载是由指控负载和协作负载两部分组成。

对于∀TDMi∈STDM，战术决策实体TDMi执行其负责的任务Tj时，由TDMi指挥控制的平台的集合记为={Pk|=1,=1,1≤k≤NP}。执行此任务Tj时，与TDMi具有协作关系的战术决策实体组成的集合为={TDMk|m=1,k≠i,1≤k≤ND}，因此定义TDMi执行任务Tj的负载为：

式（7）中，ωC2为指控负载系数，ωTC是指协作负载系数，‖j‖是指集合里元素的数目，‖‖是指集合里元素的数目。

定义TDMi在整个作战周期里面承受的负载为：

3.2.2 负载均方根的定义

考虑到组织中各战术决策实体的负载水平越均衡，组织表现出的整体作战效能越佳[5]，因此战术决策实体负载水平的均衡程度可以反映出指挥控制结构是否高效。

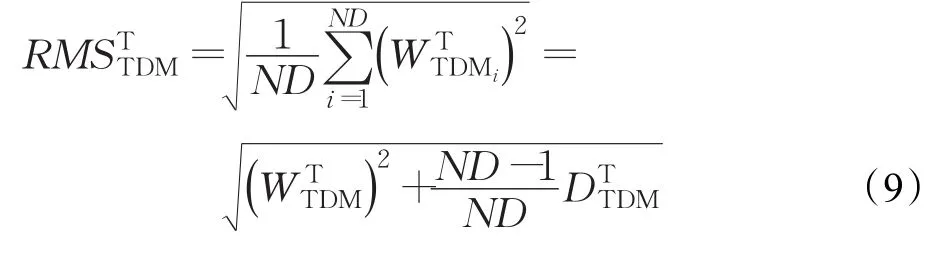
3.3 不同突发事件下的问题模型构建

战场环境具有较高的复杂性和动态不确定性，作战的进程中会出现各类复杂情况，对指控组织结构的性能造成较大影响的是行动计划发生改变和战术决策实体失效。因此，本文围绕这两种情况，研究指控组织结构的适应性调整方法。

3.3.1 行动计划变化

（1）问题描述

在作战进程中，战场环境发生变化，会导致任务增加、平台损毁等突发状况，战前的行动计划会对此进行调整。，任务与平台的关系MT-P也会根据计划的调整而改变，指挥控制组织结构需要针对变化后的任务—平台关系进行适应性调整，以保障在行动计划发生改变后，指挥控制结构能具有较好的性能，即具有较小的RM。

（2）建立模型

任务计划改变后，对指挥控制组织结构进行调整可以提升组织的性能，但组织结构的变化会给组织的稳定性带来不利影响，这就是组织的调整代价，兵力组织结构的适应性调整，不能超过组织能承受的最大代价。

调整过程里，控制权发生转移的平台数量NPTrans为：

由此，行动计划发生改变的情况下，指控结构适应性调整的模型如下：

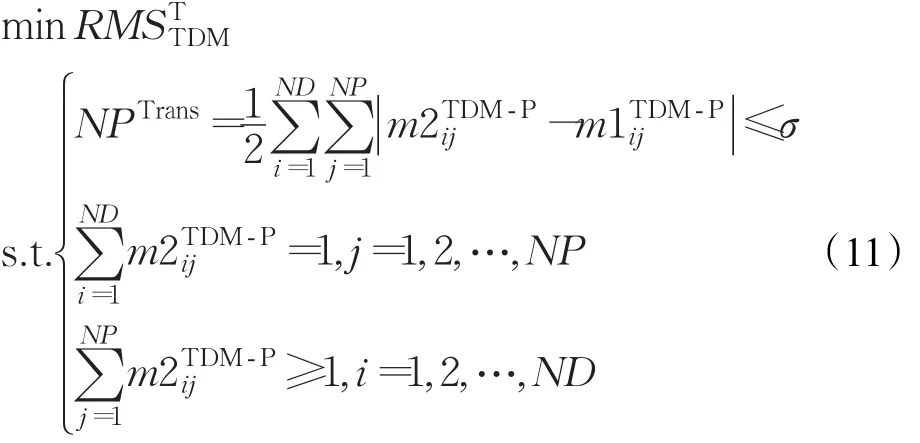
σ为组织所能承受的最大调整代价，即组织所能承受的平台控制权发生转移的最大数目。第一个约束条件表示，调整代价必须在组织的承受范围以内；第二个约束条件表示，组织内每个平台实体只能由一个战术决策实体指挥控制，第三个约束表示组织中的每个战术决策实体至少控制一个平台实体。

3.3.2 战术决策实体失效

（1）问题描述

战场上，战术决策实体是最受双方关注和打击频率最高的对象。作战过程中，某一战术决策实体受到毁坏而失效后，该战术决策实体所指挥控制的平台实体和相应的任务实体，应当由其他战术决策实体进行接替指挥，继续执行原来的任务。战术决策实体的损毁，会降低指控结构的性能，但进行适应性调整，选择出合适的替代者，则可以提高受损后指控结构的性能。

（2）建立模型

遭遇破坏前，组织内战术决策实体总数为ND，某个战术决策实体TDMND遭到破坏而失效后，战术决策实体数量变为ND-1，TDMND负责的平台实体的集合为。TDMND失效前，战术决策实体与平台实体间的指挥控制关系记为，用矩阵=()ND×NP来表示。

TDMND失效后要对TDMND所负责的平台实体进行接替指挥，把中的平台全部交由一个决策实体进行接替指挥，接替指挥后得到的指控关系用=()(ND-1)×NP表示，选择接替者的依据是，交由此决策实体进行接替指挥，相比交由其他决策实体接替指挥，得到的的RMS值最小。

综上，战术决策实体失效，指控结构的调整模型如式（12）所示：

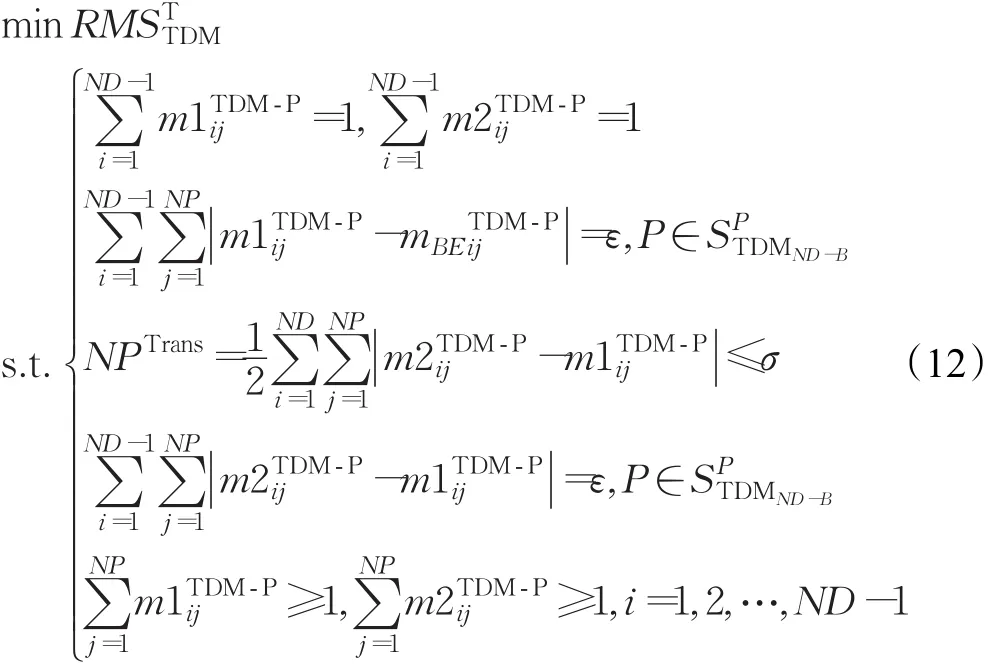
4 基于离散萤火虫算法的模型求解方法

求解模型式（11）和模型式（12），本质上都是组合优化问题寻找最优解，智能算法在解决组合优化问题上具有比较好的效果。2008年，剑桥大学的学者Yang提出了模拟萤火虫种群行为的萤火虫算法（Firefly Algorithm，FA）[9]。萤火虫算法是群智能优化算法中的一类，典型的群优化算法有蚁群算法、粒子群算法等。目前萤火虫算法已经在连续域的应用较多。通过对标准萤火虫算法进行修改而得到的离散萤火虫算法（Discrete Firefly Algorithm，DFA），目前在任务调度[10-12]、装配序列规划[13]和旅行商[14]等组合优化问题，相比传统算法有着一定的优越性，应用范围逐渐扩大[15-16]。

4.1 离散萤火虫算法

指控组织结构的适应性调整问题，属于组合优化问题，对应的求解空间属于离散的整数空间。因而，需要将标准萤火虫算法进行离散化，采用离散萤火虫算法来求解指控组织结构适应性调整问题，在指控组织结构的优化调整过程中，离散萤火虫算法的几个关键要素分别是：萤火虫位置、目标函数、距离和移动。

4.1.1 萤火虫位置的初始化及编码

算法的优化对象是，遇到突发状况后的战术决策实体与平台实体间的指挥控制关系为，用矩阵表示。寻找模型的最优解，即找到能使战术决策实体任务负载均方根RM最小的战术决策实体—平台实体系矩阵M2TDM-P。

结合组织内每个平台实体仅能由一个战术决策实体进行指挥控制的约束条件，以及每个战术决策实体至少指挥控制一个平台实体。生成和M1TDM-P矩阵相比，只有一个平台实体控制权发生转移的所有关系矩阵M={,,…,,…,}，作为算法的初始解，Q为符合条件的关系矩阵总数，也即萤火虫的总数

结合本文进行调整的指控关系矩阵MTDM-P，在编码方式上选择整数编码。

每个萤火虫都代表一个MTDM-P关系矩阵，对于任意的萤火虫i，使用n维向量 Xi=(xi,1,xi,2,…,xi,k,…,xi,n)，来表示萤火虫i的位置，n由组织中平台实体的总数来确定，即NP。xi,k∈[1,ND]，xi,k表示平台实体Pk由战术决策实体TDMxi,k指挥控制。基于此编码规则，对于如下所示的指控关系矩阵。进行编码后得到Xi=(1,3,2,4,2,1,3,1)，xi,2=3表示，平台实体P2由战术决策实体TDM3指挥控制。

4.1.2 目标函数

萤火虫算法中，亮度最高的萤火虫对应的解，即为优化问题中的全局最优解，式（11）和式（12）都是为了寻找能使RM最小的解，每个萤火虫i解码后的MTDM-P矩阵有相应的RMSi值。RMSi越小，说明此萤火虫对应的解越优，萤火虫的自身亮度I0i与RMSi成反比关系。因此把I0i的计算公式定义如下。

上式表明，计算萤火虫i的亮度时，要判断其对应的MTDM-P关系矩阵同M1TDM-P相比，平台控制权发生转移的数目是否符合幅度约束，即是否满足NPTrans≤σ。不满足幅度约束条件的解亮度值为0，随机生成满足条件的解，替代原解，并再次计算亮度值。

4.1.3 萤火虫之间的距离

两个萤火虫之间的距离反映了两种决策实体配置方案MTDM-P的差异化程度。标准萤火虫算法定义的距离基于连续域，不适用在离散空间。因此，本文用式（14）来计算萤火虫i与萤火虫 j在离散空间内的距离，进而得到两种配置方案的差异化程度。

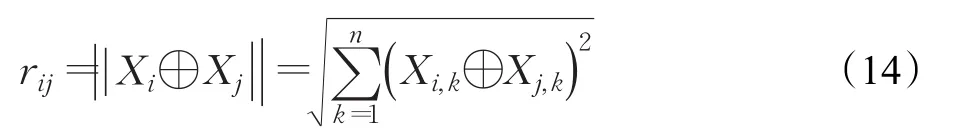
4.1.4 萤火虫的移动

针对决策实体配置方案MTDM-P的优化调整特点，重新构建萤火虫位置更新公式如下：

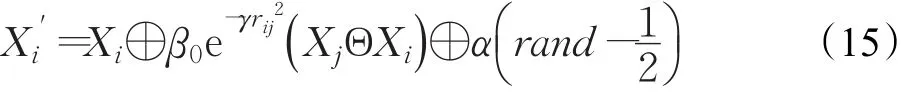
式（15）中，萤火虫移动的相关操作定义如下：

（1）位置间的减法操作XjΘXi

减法操作是用来得到萤火虫i向萤火虫 j的主移动向G。操作过程中需要对Xi和Xj进行逐维比较。

方向的数乘操作决定了Xi从Xj处继承元素的个数。在标准萤火虫算法中吸引度β决定了萤火虫的移动距离，因此本文结合2和α| rand-0.5|来决定G′从G中继承元素的数目。

（3）位置和方向的加法操作

通过以上两步的操作后，位置更新的公式可简化为式（18）。在更新位置时，若方向矢量G′中的G′k为0，则 Xi中的 xi,k保持不变。若 G′k不为0，则用 G′k替换xi,k。

4.2 离散萤火虫算法的步骤

离散萤火虫算法的具体实现步骤如下。

步骤1设置萤火虫算法的基本参数，初始化萤火虫种群，最大迭代次数MaxCycle以及光强吸收系数γ、最大吸引度β0。

步骤2按照3.2.1小节中的整数编码方法。由式（13）计算每个萤火虫的最大荧光亮度I0。

步骤3由式（14）计算，每两个萤火虫之间的距离。进而可以把距离参数用于接下来的计算。根据式（14）和式（15）计算相对亮度I和吸引度β。

步骤4根据式（15）移动萤火虫，亮度最高的萤火虫搜寻附近的最优解，并进行移动。

步骤5根据式（13）计算移动后的所有萤火虫的亮度值，对亮度进行排序，（不满足约束条件的解不参加排序，替代后的新解参与下一轮的位置下移动）此排序也是RMS值从优至差的顺序，记录下亮度最高的萤火虫的亮度值以及对应的位置。迭代次数加1。

步骤6如果达到最大迭代次数MaxCycle，结束算法并输出步骤5中保存的最优解，否则转步骤3。

对最优解进行解码，得到的MTDM-P即为使RMS最小的指控关系。

4.3 指控结构适应性调整过程

以上内容对指控组织结构适应性调整问题中的模型构建和算法求解进行了研究。任务执行过程中，产生突发事件后，首先判断事件类型，根据事件类型建立相应的调整模型，然后利用离散萤火虫算法进行求解，得到适应性调整之后的指挥控制组织结构。

5 仿真结果及分析

5.1 仿真案例

本文选择文献[19]中的联合作战案例，作为实验案例，验证离散萤火虫算法解决指控结构适应性调整问题的性能。实验在Windows 7系统环境下，使用Matlab 2014a进行仿真分析。初始的任务—平台分配关系以及战术决策实体—平台分配关系分别如表1和表2所示。关键参数设置方面，模型参数设置：指控负载系数ωC2取1，协作负载系数ωTC取2，平台控制权发生转移的最大数目取5。离散萤火虫算法参数设置：萤火虫数目Q=60，最大吸引度β0=1.0，光强吸收系数γ=1.0。

表1 初始的任务—平台关系表

表2 初始的战术决策实体—平台关系表

5.2 仿真实验

5.2.1 行动计划改变

行动计划制定了平台实体对任务实体的分配、处理关系RT-P。造成行动计划改变的情况，有任务的完成、任务取消，增加任务，平台增加和损毁，这些情况都会改变原有的行动计划，实验中突发情况随机产生，行动计划变更后，采用离散萤火虫算法对针对变化后的RT-P，对当前的决策实体配置方案进行适应性调整。

仿真实验1方法可行性验证

实验中，随机生成导致行动计划变化的情况，本次仿真生成的随机事件是平台实体P1,P5,P6,P14损毁。平台损毁后的TDM-P关系矩阵，如表3所示，作为本次仿真调整前的关系矩阵MTDM-P1。

通过离散萤火虫算法调整后得到的指控关系矩阵MTDM-P2如表4所示，调整的结果是平台实体P10的控制权发生转移，平台实体P10从由TDM1指控变为由TDM3指控。

调整前，MTDM-P1对应的RMS值为36.814 4，适应性调整后得到的MTDM-P2对应的RMS值是31.827 8，RMS值降低明显，说明在本次仿真中本方法对指控组织结构进行了合理的优化。

仿真实验2方法的性能比较

实验1为单次仿真的结果，在行动计划改变的情况下，进行20次仿真实验，验证本方法的有效性，同时也和其他方法进行对比分析。对于每次仿真，致使行动计划改变的突发情况都采用随机生成的办法。贪心搜索算法（Greedy Search Algorithm，GSA）也能较好地用于解决该问题[8]，离散人工蜂群算法（Discrete Artificial Bee Colony Algorithm，DABC）作为较为新颖的解决组合优化的启发式搜索算法[17-18]，也可用于求解本文的模型，因而将离散萤火虫算法同这两种算法进行对比。实验结果如图2和图3所示。

表3 平台损毁后的指控关系矩阵

表4 调整后的指控关系矩阵

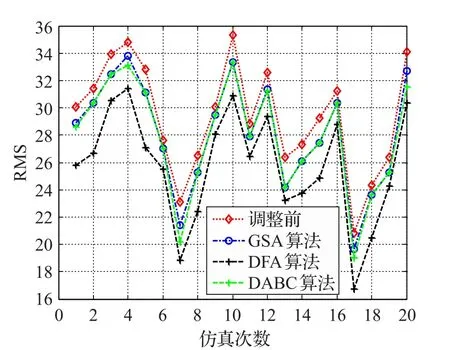
图2 性能对比图

图3 算法耗时对比图

5.2.2 决策实体失效

情形1的突发情况致使行动计划做出改变，情形2在行动计划改变的基础上，增加战术决策实体失效的情况。仿真中随机确定失效的决策实体。对失效之后的决策实体进行接替指挥，图4中红线部分代表接替后的RMS值。

仿真实验1方法可行性验证

本次仿真中出现了战术决策实体TDM3损毁，行动计划变化上为P18损毁，新增平台P21与P22。TDM3失效后的关系矩阵如表5所示。TDM3所负责的平台P7,P12,P13,P20交由TDM4接替指挥，交由TDM4指挥控制是剩余三个决策实体中RMS值最低的接替方法。接替指挥后得到的指控关系如表6所示。

仿真实验2方法的性能比较

针对情形2，进行20次仿真实验，对算法效果进行验证，突发事件均随机产生同样采用离散萤火虫算法、贪婪贪心搜索算法和离散萤火虫算法这三种算法，仿真结果如图4、图5所示。

5.3 仿真分析

在情形1的仿真实验中，由图2可以看出采用DFA算法、GSA算法和DABC算法，指控组织结构调整后的RMS值均低于调整前的RMS值，说明此三种方法都能解决此问题。采用DFA算法得到的RMS值降低幅度最大，说明DFA算法在解决指控组织结构适应性调整的效果优于DABC和GSA算法，DABC和GSA算法的效果较为接近。在算法耗时上DFA算法的耗时最低，GSA的耗时最高，说明DFA算法的效率最高。

表5 战术决策实体失效后的指控关系矩阵

表6 进行接替指挥后的关系矩阵

表7 调整后的指控关系矩阵

图4 性能对比图

图5 算法耗时对比图

情形2的仿真实验中，从图4的结果上可以看出，三种算法中，采用DFA算法和DABC算法降低RMS值更加明显，在大部分仿真中，DFA算法的效果优于DABC算法。图5对三种算法的耗时情况进行比较，采用贪婪算法的耗时显著高于DFA算法和DABC算法，DFA算法耗时最短。

综上，采用DFA算法可以更好地降低负载均方值，并且在算法耗时上有较大优势，更能够满足战场环境下，指控结构调整对时效性的要求。

6 结束语

本文研究了指挥控制组织结构的适应性调整问题，基于离散萤火虫算法提出了解决指控结构适应性调整方法，分别在两种作战情形下对算法进行仿真验证，并与贪心算法以及离散蜂群算法进行对比，验证了离散萤火虫算法用在指控结构调整中的可行性以及高效性。