最小化误差平方和k-means初始聚类中心优化方法

周本金，陶以政，纪 斌，谢永辉

中国工程物理研究院 计算机应用研究所，四川 绵阳 621900

1 引言

聚类是依照某种相似度度量标准，将数据集划分成多个簇的过程，其目的是最大化簇内相似度，最小化簇间相似度。目前聚类已经广泛应用于多个领域，包括商务智能、模式识别、异常检测、信息检索[1]等领域。聚类也可以作为其他算法的预处理步骤。

k-means作为聚类算法中的一种，自MacQueen于1967年提出以来，因为其实现简单、时间开销低并且适合于并行计算[2]，目前已经得到了广泛应用。传统的k-means算法是一种启发式的贪心算法，常常得到的是一个局部最优解，聚类效果很大程度取决于初始中心点的选择。鉴于上述不足，很多学者对其提出了优化方法。以PAM算法为代表的k-medoids聚类算法以及其改进算法[3]，尽管算法能够取得比较良好的聚类效果，但是时间开销过大，不适合大规模数据聚类。最近几年新兴的模拟退火算法[4]和遗传算法[5]，其目的是获取全局最优解，不过在实践中这些方法没有被广泛接受。本文主要针对k-means对初始聚类中心敏感进行优化。目前优化方法大体分为两种，一种是基于距离的，另一种是基于密度的方法。基于距离的方法主要优点是时间开销较小，不过无法反映数据点的分布信息，容易选取到孤立点。常见的有最大最小距离法[6]，该方法选取距离已有聚类中心距离之和最大的数据点作为下一个聚类中心，但是该方法对孤立点过于敏感。基于密度的方法通常能够比较准确地反应数据的分布情况，不过计算开销较大。文献[7-9]提出了样本密度的概念，通过选择密度最大且相互远离的数据点作为初始聚类中心点，通过设定参数调节样本的邻域半径，并计算邻域内样本数目作为样本密度，但是参数的设置缺乏客观性，需要先验知识或者经验。文献[10]通过计算样本方差的形式，选择样本方差较小数据点作为聚类中心，能够有效地降低误差平方和；文献[11]通过计算所有数据点的紧密性，将高紧密型的数据点集合作为候选聚类中心集合，选择紧密性最大的数据点作为第一个聚类中心，之后按照最大最小距离原则，选择后续的聚类中心。

2 k-means算法

2.1 经典k-means算法

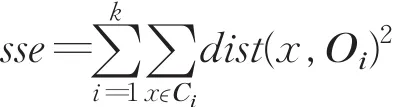
其中k为簇的个数，Oi是第i个簇Ci的聚类中心，dist(x,Oi)指的是数据点x与Oi的相异度，不同的相异度计算常常会导致不同的聚类结果[12]，通常采用欧式距离度量。

定义2欧式距离

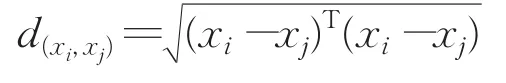
定义3簇Ci的聚类中心Oi

k-means是一种迭代重定位方法，主要有两个步骤，步骤1是依据最近邻原则将数据点分配到距离最近的中心点；步骤2是重定位，即重新计算聚类中心。如此反复，直到到达指定的收敛条件，聚类结束。

k-means以最小化误差平方和（简称sse）为目的，sse定义如下：

定义1误差平方和

2.2 改进算法minSseKmeans

传统的聚类中心选择方法由于是随机选择，容易选取到孤立点，或者多个数据点位于同一个类中，导致聚类结果质量较差。由于数据选择的随机性，聚类结果也不稳定。一个良好的初始聚类中心集合，应该使得每一个类中都有一个数据点被选择到，并且数据点越接近实际的聚类中心，效果越好。

2.2.1 基本原理

不同于目前已有的k-means初始中心优化算法，本文是通过最大化减少sse的值来获得初始聚类中心集合。k-means算法本身是以最小化sse为目标，每次聚类迭代的过程中，实际上都是sse逐步减少的过程，如果初始聚类中心集合的sse能够达到最小，那么不仅能够减少聚类的迭代时间，同时较小的sse一定程度上能够有效地避免选取到孤立点，后面的人工模拟数据能够充分体现该点。本文提出的minSseKmeans算法就是基于这一原理提出。

为了在聚类初始中心选择阶段获取较小的sse，Mt表示t次迭代之后所获得的t个初始聚类中心数据点(t＜k)集合，在选择第t+1的聚类中心Zt+1的时候，显然会降低sse的值，因为至少有一个数据点（实际上是Zt+1本身）到Mt中聚类中心的最小距离要大于它到自身的距离。基于这样的原则，从数据集中选择初始聚类中心的时候，选择能够最大程度地减少sse的数据点作为下一次聚类中心。即在第t+1次迭代的过程中，第t+1个聚类中心Zt+1应该满足（D是数据集集合）。

定义4

定义5

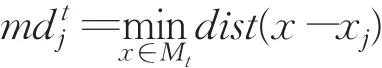
定义6

diffSSE(i)是将第i个数据点xi设置为聚类中心时候能够减少的sse，mdtj是第 j个数据点xj在t次迭代之后到目前选择到的聚类中心数据集合的最小距离。

2.2.2 基本步骤

为了减少不同量纲对聚类的影响，需要对数据标准化，采用离差标准化方法，使得数据落在[0，1]区间上。

定义7

其中maxp和minp分别是p属性上的最大和最小值。

minSseKmeans步骤如下：

（1）利用定义7对数据集中的数据进行标准化，迭代次数t=0。

（2）计算数据集中数据点之间相互距离。

（3）如果t=k，那么算法终止。否则转到步骤（4）。

（4）如果‖ ‖M =0，说明聚类中心集合中还没有一个数据点，根据定义1，以数据集中每个数据点作为聚类中心，计算其所对应的sse，选择最小的sse对应的数据点作为第一个初始聚类中心Z1，并加入集合M中，记录数据点xj到Z1的距离md1j；否则，根据定义6选择能够最大程度地减少sse的数据点作为第t次迭代的聚类中心Zt，加入集合M 。

（5）更新数据集中的所有数据点xj到集合M中的最短距离mdtj。迭代次数t自增1，转至步骤（3）。

2.2.3 算法复杂度分析

步骤（2）计算数据点之间距离时间开销是O(n2)。步骤（4）最外层循环是k次，表示需要选择k个聚类中心，每次迭代过程中，计算数据集中每个数据点Z作为下一个聚类中心能够减少的sse。由定义4可知，计算diffSSE的时候，需要比较数据集每个数据点上次迭代的最短距离和Z的距离，所以计算一个数据点的diffSSE的时间开销是O(n)，而每次迭代需要比较所有的数据点，所以每次迭代算法复杂度是O(n2)，步骤（4）总的时间复杂度是O(kn2)。结合步骤（2）和步骤（4），文中minSseKmeans算法复杂度是O((k+1)n2)。

3 实验验证

实验部分数据集分为人工模拟数据和真实数据，对比的两个方法分别是文献[6]中的基于最大距离法以及文献[10]中基于最小方差优化初始聚类中心方法。聚类质量评价目前有很多个指标，当事先知道数据点所属分类时候采用外在方法，当数据点所属分类事先未知采用内在方法。由于采用的数据集已经有基准类别信息，所以采用BCubed[13]外在度量方法，其主要分为两个度量指标，精准度Precision和召回率Recall。为了全面地评价聚类的好坏，采取二者的调和均值F作为聚类结果的综合评价指标。实验平台采用Win8.1操作系统、i7-4710MQ 2.5 GHz处理器、Matlab2014。

定义8

定义9

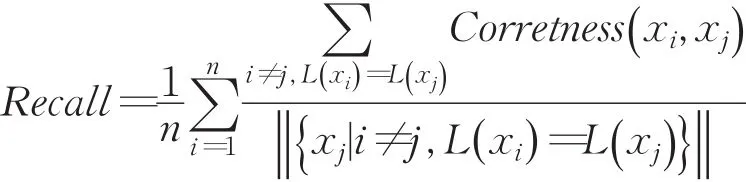
其中L(xi)是基准确定的xi的类编号，P(xi)代表聚类结果中xi所属的簇编号。

定义10

3.1 真实数据集

测试数据集描述信息如表1所示（其中CMC数据集是Contraceptive Method Choice数据集的缩写）。数据集按照样本数从低到高排列，覆盖了多种类型的数据分布，包括高维数据（属性个数10个或以上）集、非均匀数据集（Indians Diabetes）以及混合型数据类型数据集（Ecoli）。对分类属性的均值，采用众数计算方法。聚类评价的指标包括聚类时间、迭代次数以及F值，实验次数50。

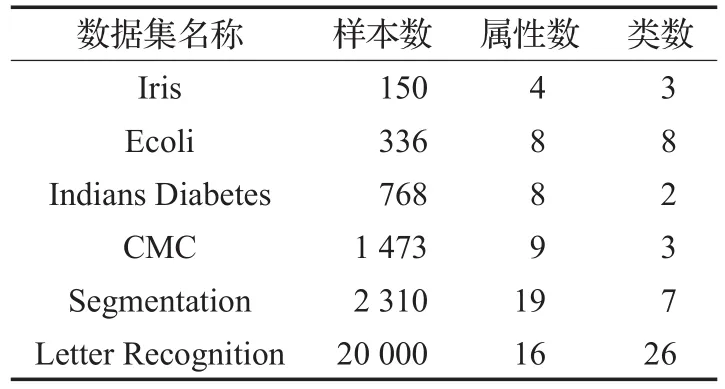
表1 UCI数据集描述信息

3.1.1 聚类时间对比

除了传统的k-means算法外，其他两种算法时间复杂度和本文相同，都是O(n2)，不过n2对应的常数项要低于本文算法，对于规模不大的数据，彼此之间的时间差距并不明显。对于文中的大部分数据集，本文算法时间开销都低于其他两种算法，主要是因为时间开销由两部分组成，前一部分是初始聚类中心的选择，后一部分才是真正的聚类，当数据集较少时候，后一阶段聚类部分时间开销占主要成分。由于minSseKmeans以最大程度的减少sse为目的，导致选择初始聚类中心之后所获得的sse是4个算法中最少的，使得后一阶段的聚类的迭代次数减少，所以时间开销要低于其他两种算法。当数据集规模较大时候（比如Letter Recognition数据集），本文算法时间开销要显著高于其他算法。Ecoli数据集是唯一一个混合型属性的数据集，时间开销较大。主要在于计算分类属性距离的时候，比较的是字符串，而字符串比较的开销要显著高于单纯的数值比较。聚类时间如表2所示。

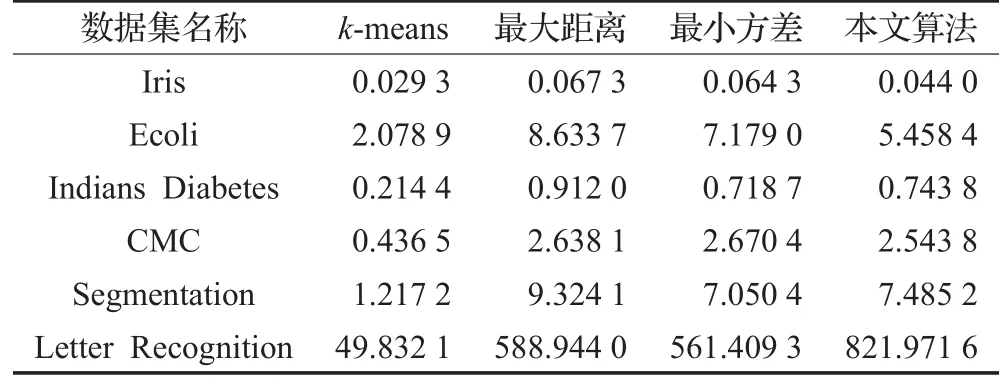
表2 聚类时间 s

3.1.2 F值比较

实验结果如图1所示，4种聚类方法在Letter Recognition上的F值都不到17%，说明该数据集聚类趋势不明显。另一方面，Letter Recognition本身类的数目和属性较多，由于文中采用的是欧几里德距离度量方法，而该度量方式容易受变量多重相关性[14]和噪声影响[15]，当对高维数据进行聚类的时候，由于变量相关性影响会出现维度灾难[16]，使得不同簇之间区分度进一步下降，所以导致最终聚类效果较差。鉴于此，在聚类开始前需要对高维数据进行降维[17]。由于F值过低，没有实际的对比价值，后面的验证部分不再使用Letter Recognition数据集。5个数据集中，只有Ecoli数据集，minSseKmeans算法所对应F值不是最高。主要原因在于Ecoli有一个分类属性，在对数据进行标准化之后，会导致数值型属性所占的权重低于分类属性，致使分类属性对数据集的聚类效果的贡献程度大于其他数值型属性。

图1 聚类效果F值比较

尽管本文算法相较于其他三种算法聚类质量提升程度不明显，不过相较于其他两种优化初始聚类中心算法，本文算法相对于传统的k-means算法在5个数据集上聚类质量都有所改善，平均F值提升8%，而其他两种算法往往只是针对于某种类型的数据的聚类质量好于传统k-means。尽管本文算法时间复杂度高于其他两种算法，但是当簇的个数相对较少，数据集规模不大的情况下，本文算法时间复杂度和其他两种算法时间差异并不明显。

3.1.3 迭代次数以及sse比较

一个好的初始聚类中心应该尽可能地靠近真实聚类数据的聚类中心，同时能够很大程度减少后续聚类阶段迭代次数。因此迭代次数一定程度能够体现初始聚类中心的优劣。由图2可以看出，在5个数据集中，本文算法中的迭代次数总是最少的，主要是因为minSseK-means方法在获得初始聚类中心所对应的sse是4个算法中最小的，在后期聚类阶段达到收敛条件所需要的迭代次数自然较少。

图2 迭代次数对比

最终聚类结束之后各个算法的sse如表3所示，对于大部分数据集来说，本文算法的sse较小。

表3 真实数据集sse对比

3.2 人工模拟数据

为了测试该算法相对于其他两种算法对孤立点不敏感，不需要像其他基于密度的算法[18]需要事先选择高密度的数据点作为候选初始聚类中心。为此人工生成了一些模拟数据。

由minSseKmeans的步骤中不难看出，该方法不太可能选取到孤立点。在初始聚类中心选择阶段，当选中当前数据点 pi作为聚类中心的时候，计算该数据点到数据集中的其他数据点 pj的距离dist(i,j)，设当前pj距离当前聚类中心集合的最短距离为dmin，只有当dist(i,j)小于dmin的时候，才能够减少当前sse。而k-means中孤立点通常指的是全局离群点，全局离群点定义为显著偏离数据集中的大部分数据点。假设选择孤立点作为聚类中心，由于大部分的数据点都远离孤立点，会导致diffSSE(i)较小，相对于数据集中的正常点，孤立点不太可能作为聚类中心。

人工生成了3个符合高斯分布的二维数据点，每个簇有100个数据点。然后人工添加指定比率的孤立点，表4是模拟数据参数信息。其中σo表示孤立点数据高斯分布所对应的标准差。

表4 人工模拟数据点参数信息

为了更清楚地显示聚类中心选择的最终结果，从多个模拟数据集中选取了一组孤立点比例为0.1的数据点集合进行分析。图3是数据点二维分布。其中+号代表实际的聚类中心。

图3 模拟数据二维空间分布

采用不同比例的孤立点数据，分别使用最大距离法、最小方差法以及本文的minSseKmeans算法对人工模拟数据进行聚类，获得初始聚类中心。比较sse，结果如表5所示。

表5 模拟数据聚类最终sse

由表5容易看出，三种方法中，minSseKmeans总是能够获得最小的sse。sse最大的总是最大距离方法，因为该方法初始两个聚类中心选择的是数据集中距离最大的两个数据点，这种方式很容易选取到位于两个相距较远的孤立点。

初始聚类中心结果如图4所示。三种算法都受到了孤立点的影响，导致它们所获得初始聚类中心都较大程度地偏离实际的聚类中心，其中最大距离法选取的初始聚类中心偏离程度最大，甚至有两个聚类中心是孤立点，另一个聚类中心偏移实际簇中心较远。最小方差方法聚类效果相对次之，只选取到一个孤立点。minSseK-means效果最好，从图中容易看出三个聚类中心彼此远离，并且有两个聚类中心比较接近实际的聚类中心。

图4 孤立点比例0.1聚类初始中心结果

4 结束语

针对k-means算法对初始聚类中心敏感问题，以最大程度减少当前sse为思想，提出了minSseKmeans方法，该方法简单而且容易理解。使用UCI真实数据集和人工模拟数据集，同其他已知的优化k-means初始聚类中心的算法进行对比，结果显示该算法在选择初始聚类中心方面不仅减少了聚类的迭代次数，而且提高了聚类质量，同时该算法对孤立点不敏感。不过该方法算法复杂度较高，当数据集规模较大的时候可以采取多次随机取样的方式，计算每个样本的sse，选择具有最小sse的样本所对应的聚类中心作为初始聚类中心。

尽管该方法能够有效的选择合适的初始聚类中心，但k-means的聚类质量还和后面的重定位阶段有关。单纯拥有好的初始聚类中心，并不能保证聚类效果一定较好。主要是因为在重定位阶段新的聚类中心的计算对孤立点过于敏感，在进行均值计算的时候，孤立点很可能使聚类中心偏离实际的聚类中心。所以后续阶段还需要对k-means重定位阶段进行优化，能够将孤立点有效地筛选出来。