有限自动机可识别语言的基数

迟晓晴，王玉涵，王艳慧

山东科技大学 数学与系统科学学院，山东 青岛 266590

1 引言

自动机是计算理论中最简单的数学模型[1]。它不仅是计算机科学理论的基础，而且与神经网络和模型论等领域密切相关[2-3]。有限自动机在软件工程、句法分析、形式语言和程序语言等多个领域得到了有效的应用[4-6]。由于自动机具有固定的内在状态、记忆能力和识别判断能力或决策能力，因此它适宜于作为一切信息系统的数学模型[7-9]。特别的，在形式语言方面，自动机提供了一种处理语言的可靠工具[10-11]。自动机可识别语言[12-14]是形式语言与自动机理论研究的一个重要领域[15-16]。

从图论的角度讲，自动机可看作一个有向图。利用图的邻接矩阵可研究图中的路及图中任意两个结点间的可达性等问题。对于一个字符集Σ上的有限自动机M，一个字w∈Σ*（Σ*是Σ上有限字符串的集合）可被M识别当且仅当在w的作用下，按照状态转移函数，自动机由初始状态到达终止状态。这表明，如果把自动机看作一个有向图，可利用其邻接矩阵，研究该自动机可识别的语言。因此，本文利用有向图的邻接矩阵研究有限自动机可识别语言的基数问题。

2 有向图的邻接矩阵

简单回顾有向图及其邻接矩阵的相关知识，详见文献[18]。

一个图是一个三元组 V(G),E(G),φ(G)，其中V(G)是一个非空的结点集合，E(G)是边集合，φ(G)是从边集合E到结点元序偶（有序偶）集合上的函数。若把图中的边e∈E(G )看作总是与两个结点关联，那么一个图亦可简记为G=V,E ，其中V是非空结点集，E是连接结点的边集。若边e与结点有序偶 vi,vj相关联，则称该边为有向边。每一条边都是有向边的图称有向图。每一条边都有权值的有向图称赋权有向图。

根据文献[18]中简单图的邻接矩阵的定义，任意一个有向图的邻接矩阵的定义如下：

定义1设G=(V,E)是一个有向图，它有n个结点V={v1,v2,…,vn}。则n阶方阵A(G)或(aij)称为G的邻接矩阵，其中aij=k，若从vi到vj存在k条边，k∈N0。

注1在有向图同构的意义下，有向图与其邻接矩阵存在一一对应的关系，即有向图确定时，其邻接矩阵唯一确定，反之，邻接矩阵确定时，其对应的有向图唯一确定。

例1设图G如图1所示，其邻接矩阵为：

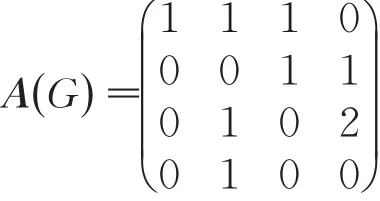
图1 有向图G

文献[17]中证明，若A(G )是一个简单图G的邻接矩阵，则A(G)m中的i行、j列元素表示等于G中联结vi与vj的长度为m的路的数目。下面证明此结论对任意一个有向图的邻接矩阵仍然成立。

引理1[18（]乘法原理）若完成一件事情要经过两个步骤，其中第一步有n1种不同的方法，第二步有n2种不同的方法，对完成这件事情共有n1n2种方法。

定理1设A是有向图G的邻接矩阵，其中V={v1,v2,…,vn}，则Am中的i行、j列元素等于G中从结点vi到vj的长度为m的路的数目。

证明 对m用数学归纳法。

当m=1时，由定义1可知显然成立。

当m≥2时，假定命题对m成立，由

Am+1=Am·A故

3 有限自动机及其可识别语言

为保证本文知识的完整性，本章回顾有限自动机及其可识别语言的一些基本概念。

定义2[19]有限自动机M是一个五元组M=(Q,Σ,δ,q0,F)，其中，Q是一个非空有限集合，称为状态集；Σ是一个非空有限集合，称为字符集；q0∈Q是M的初始状态（或开始状态）；F⊂Q是M终止状态的集合；δ：Q×Σ→Q是一个映射，称为状态转移函数。

对于一个有限自动机 M=(Q,Σ,δ,q0,F)，每个q∈Q称为M 的一个状态。若q∈F，则q是M的一个终止状态（或接收状态）。对任意的(q ,a)∈Q×Σ，p∈Q ，δ(q ,a)=p表示M在状态q读入字符a时，其状态由q转移到 p，即：

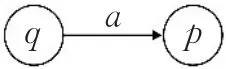
因此，按照结点表示状态，边表示遵循δ的状态转移，有限自动机M可以用一个赋权有向图来表示。与M对应的赋权有向图M′的结点集合是Q，边集合V={(q,a,p):q,p∈Q,a∈Σ,δ(q,a)=p}。

例2给定有限自动机M=(Q ,Σ,δ,q0,F )，其中Q=(q0,q1,q2,q3)，Σ={a ,b}，F={q3}，δ：Q×Σ→Q定义为：

δ(q0,a)=q1，δ(q0,b)=q3

δ(q1,a)=q3，δ(q1,b)=q2

δ(q2,a)=q2，δ(q2,b)=q2

δ(q3,a)=q2，δ(q3,b)=q2

与M对应的赋权有向图M′如图2所示。

图2 有向图M′

若Σ是一个非空有限的字符集，则Σ*是Σ上有限个字符构成的字符串的集合，即Σ*={a1a2…an:a1,a2,…,an∈Σ,n∈N0}。这里Σ*含有空字符ε。给定一个有限自动机M=( )Q,Σ,δ,q0,F ，其状态转移函数δ可以诱导定义一个从Q×Σ*到Q的映射，即δ：Q×Σ*→Q，其作用法则对任意的q∈Q，w∈Σ*。

若对任意的w∈Σ*，δ(q0,w )∈F，则称w可被自动机M识别（或接受）。

在例2中，若取q=q0，w1=abab，则：

δ(q0,a)=q1，δ(q1,b)=q2

δ(q2,a)=q2，δ(q1,a)=q3

即，在图2中：

则δ(q0,w1)=q2∉F，从而w1不能被自动机M识别。

若取 q=q0，w2=a2，则：

δ(q0,a)=q1，δ(q1,a)=q3

即，在图2中：则δ(q0,w2)=q3∈F，从而w2可被自动机M识别。

注2 若w=a1a2…an∈Σ*被有限自动机M=(Q,Σ,δ,q0,F)识别，则在与M对应的赋权有向图M′中存在一条由w作为权值的从q0到q(q ∈F)的路，即，其中qin=q∈F。反之，因M 与M′一一对应，故若在M′中，存在从q0到q(q ∈F)的路，即qjm，其中qjm=q，则b1b2…bm可被有限自动机M识别。给定一个有限自动机M=(Q ,Σ,δ,q0,F )，Σ*中所有可被M识别的字符串的集合称为有限自动机M可识别的语言，记作L(M )。

例2中L(M )={b ,a2}。

4 有限自动机可识别语言的基数

利用有向图的邻接矩阵研究有限自动机可识别语言的基数。一个集合S含有元素的个数称为这个集合的基数（或势），记作 ||S。

一个有限自动机M=( )Q,Σ,δ,q0,F ，对应的有向图记作M′。对任意的q∈F，Pq表示M′中从q0到q的所有路的集合。令

由注2知，PF与L(M )一一对应，因此可得：

命题1对于一个有限自动机 M=(Q,Σ,δ,q0,F)，则 | L(M ) |=| PF|。

一个有限自动机M=(Q ,Σ,δ,q0,F )对应的有向图M′的邻接矩阵A(M ′)是一个 | Q|×|Q |的方阵，用Q标识A(M ′)的行和列。由定理1知，对任意的q∈F，[A (M ′)]m中q0行，q列的元素表示的是M′中从q0到q的长度为m的路的数目。因此：

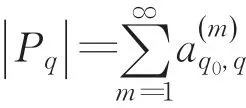
定理2对于一个有限自动机M=(Q,Σ,δ,q0,F)，

例3给定一个有限自动机M=(Q,Σ,δ,q0,F)，其中Q=(q0,q1,q2,)，Σ={a}，F={q2}，δ：Q×Σ→Q 定义为：

δ(q0,a)=q1

δ(q1,a)=q2

δ(q2,a)=q2

与M对应的有向图M′如图3所示。

图3 有向图M′

例4自动咖啡机M售出一杯咖啡15元，M只接受5元和10元的纸币。在确定收到足够的钱时它处于4种状态q0、q1、q2、q3。M 在投入新的纸币后改变状态，且终止状态只接受最终金额为15元。与M=(Q,Σ,δ,q0,F)对应的有向图如图4。

图4 咖啡机M

其中Q=(q0,q1,q2,q3)，Σ={a ,b}，F={q3}，a和b分别表示输入的纸币金额为5元和10元。易知咖啡机M的邻接矩阵为：

从而

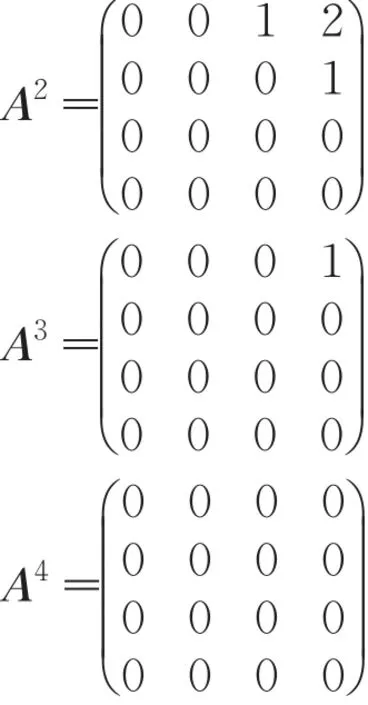
两个有限自动机M1和M2等价当且仅当L(M1)=L(M2)。因此若M1和M2等价，则L(M1)和L(M2)中含有长度为m(m ∈N )的字的数目必相等。由定理1可得M1和M2不等价的一个充分条件。

推论1对于两个有限自动机M1=(Q1,Σ,δ1,q0,F1)和M2=(Q2,Σ,δ2,q0,F2)，若存在m∈N ，使得，则 M和 M不等价。12

5 结论

利用有向图的邻接矩阵给出了有限自动机的可识别语言的基数公式，讨论了判定两个自动机不等价的充分条件。这些工作将有限自动机与矩阵联系起来，为应用矩阵理论处理一些自动机问题奠定基础。