硬质聚氨酯泡沫动静态劈裂拉伸的试验研究

江 伟，卢玉斌*，姜锡权，段俊舟

(1.西南科技大学制造过程测试技术教育部重点实验室，四川 绵阳 621010； 2.陆军炮兵防空兵学院先进材料动力学实验室，合肥 230031)

0 前言

RPUF作为一种轻质、疏松、蜂窝状的结构材料，其质量轻、比强度高、抗疲劳性能好，具有良好的冲击吸能特性以及隔音、绝热和减振性能，因此常用来作为人们日常生活中的结构、包装以及防护材料，具有广阔的应用前景。在实际工程应用中，RPUF通常是承受压缩载荷，而由于材料的抗压能力相对抗拉能力较高(抗压强度约为抗拉强度的3倍)，这就使得材料在压缩载荷作用下间接(3点弯曲、劈裂等)地导致其拉伸失效。因此，对RPUF劈裂拉伸的研究就显得至关重要。

目前，关于RPUF材料拉伸性能的研究, 国内外也展开了广泛的研究。伍壁超等[1]从密度、应变率、取向、温度等方面在MTS实验机上对哑铃型RPUF板材试件进行了准静态拉伸实验。发现在弹性阶段应变率效应并不明显，而在塑性阶段抗拉强度却随应变率的增大而减小；从0 °、45 °和90 ° 3个取向研究发现具有一定的各向异性；另外，无论高密度还是低密度，RPUF的抗拉强度与弹性模量都会随温度的升高而降低且高密度下降幅度相对较大。

陈诚[2]对RPUF进行了6种不同应变率下的准静态拉伸试验和数值模拟，发现RPUF的断裂表现明显的脆性特征，并且拉伸断裂强度与弹性模量随着应变率的增大而增大，而拉伸断裂应变却表现相反的规律。

付顺强[3]采用旋转盘式间接杆型冲击拉伸实验装置对硬质泡沫塑料(聚碳酸酯棒材)进行了动态拉伸，并从准镜静态和动态2个方面对比研究，结果表明该种材料表现明显的非线性、黏弹性特征，而且其力学性能具有明显的应变率相关性，屈服应力和失稳应变随应变率的增加而显著增大。

(a)双立柱微机控制电子万能试验机 (b)非接触应变测量系统 (c)霍普金森压杆图1 试验设备Fig.1 Test device

Ridha等[4]从RPUF的加载方向、材料密度和泡孔各向异性等角度对其拉伸变形响应进行了研究。结果表明：该种泡沫材料表现明显的各向异性，刚度和强度随着加载方向和泡沫上升方向之间的角度增大而减小，随着密度的增加而增强，并且力学性能中的各向异性与几何单元中的各向异性有一定的相关性。

Kabir等[5]在准静态试验中研究了不同密度、微结构下硬质聚氨酯泡沫塑料的拉伸、准静态断裂和动态断裂的力学特性，发现拉伸强度和弹性模量强烈依赖于泡沫密度，而且其断裂韧性也往往依赖于泡沫密度以及微观结构。

Doroudiani等[6]研究了聚苯乙烯(PS)泡沫塑料泡孔结构对其拉伸力学性能的影响，分别对相同泡孔尺寸、不同泡沫密度以及相同泡沫密度、不同泡孔尺寸的PS泡沫塑料的拉伸性能进行测试。研究发现，随着相对密度的增大，泡沫塑料的相对拉伸强度呈幂指数关系显著增大；随泡孔尺寸的增大，泡沫塑料的相对拉伸强度会有所下降。

卢子兴等[7]通过准静态试验对3种不同密度的硬质聚氨酯泡沫塑料的拉伸本构关系及其失效机理进行了研究。发现高密度聚氨酯泡沫塑料的弹性模量和抗拉强度均随其密度的增加而增大，而断裂应变则随密度的变化没有明显的规律性。此外，还说明了硬质聚氨酯泡沫塑料在拉伸应力状态下的脆性变形特征。

综上所述，以上学者主要是基于硬质聚氨酯泡沫塑料的准静态直接拉伸力学特性的研究，而关于RPUF的动态拉伸很少有人涉足，尤其是RPUF的动态劈裂拉伸，目前还没有学者进行相关的研究。因此，很有必要对其进行动态和静态劈裂，对间接研究RPUF的破坏形式及拉伸力学性能具有重要意义。本文利用MTS试验机并结合应变分析测量系统对密度为0.54 g/cm3和0.62 g/cm3的2种RPUF进行准静态劈裂以及利用分离式霍普金森压杆对密度为0.62 g/cm3的RPUF进行动态劈裂，试验研究主要考虑应变率、密度和长径比3个影响因素。

1 实验部分

1.1 主要原料

高密度RPUF，由多元有机异氰酸酯与多元醇(聚醚多元醇或聚酯多元醇)反应产生，材料密度为0.54、0.62 g/cm3，热导率分别为0.022、0.024 W/(m·K)，闭孔率均高于95 %，北京京都顺发保温材料有限公司。

1.2 主要设备及仪器

双立柱微机控制电子万能试验机(MTS)，WDW-100，上海百若试验仪器有限公司，如图1(a)所示；

非接触应变测量系统，XJTUOM，西安交通大学，如图1(b)所示；

钨灯丝扫描电子显微镜(SEM)，EVO18，德国蔡司公司；

霍普金森压杆，SHPB，陆军炮兵防空兵学院，如图1(c)所示。

1.3 样品制备

根据试验研究方案对试样进行加工，试验试件形状均为圆柱体，尺寸允许误差范围为0.1～0.3 mm；

在静态劈裂试验中，对应变率效应的研究，所用材料密度为0.54 g/cm3和0.62 g/cm3，试件尺寸均为Φ74 mm×37 mm；而对试件长径比的研究，所用材料密度为0.62 g/cm3，由于考虑0.4、0.5和0.8这3种长径比，对应的试件尺寸分别为Φ50 mm×20 mm、Φ50 mm×25 mm和Φ50 mm×40 mm，试件均加工成平台巴西圆盘，中心角为2α=20 °，如图2所示；

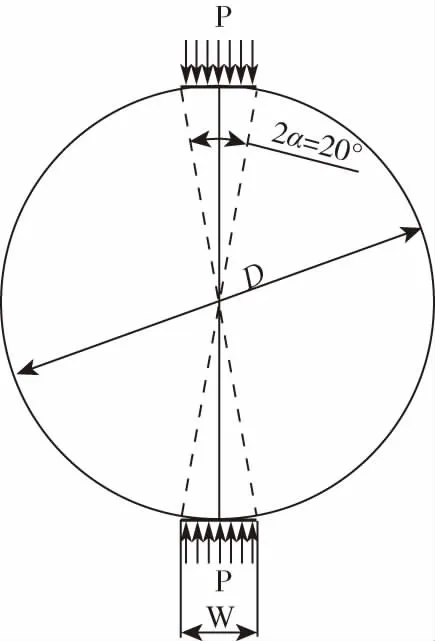
图2 准静态劈裂加载示意图Fig.2 Loading diagram of quasi-static split

在动态劈裂试验中，所用材料密度均为0.62 g/cm3，对于应变率效应的研究，试件尺寸为Φ50 mm×25 mm；对于长径比的研究，考虑0.2、0.4、0.6、0.8这4种长径比，对应的试件尺寸分别为Φ50 mm×10 mm、Φ50 mm×20 mm、Φ50 mm×30 mm、Φ50 mm×40 mm；试样均为巴西圆盘(无平台)，但为了保证试样从中心起裂，本实验设计了一定宽度的弧形垫条，以形成中心角为2α=20 °的平台；该种方法相对于巴西圆盘，克服了加载端处的应力集中现象，使得两端在加载过程中处于均匀加载状态，从而使试件破坏时能够沿其中心线开裂；其平台宽度(w)取决于试件的中心角，垫条式平台巴西圆盘的加载示意图，如图3所示。

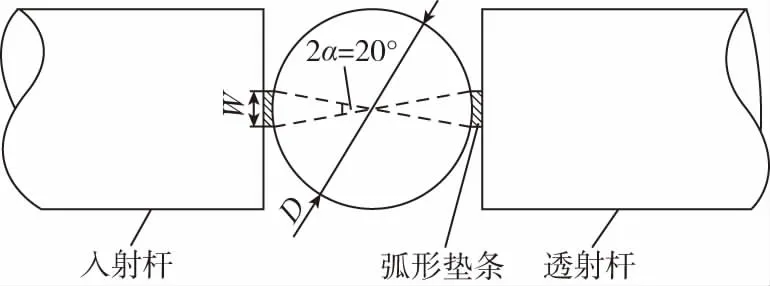
图3 动态劈裂加载示意图Fig.3 Loading diagram of dynamic split

1.4 性能测试与结构表征

准静态劈裂试验是在承载力为100 kN的MTS上进行，同时结合非接触式三维动态应变测量系统(VIC-3D)对材料的位移场和应变场进行实时记录和分析。试验前，需对散斑系统进行调试，调试完毕后将试件放于压盘中心下方，调整试件位置，使得相机的校正中心线与试件中心线重合，然后开启图像采集并同时启动伺服。其中，应变率效应研究中，RPUF的加载速度分别为2、10、20、30 mm/min；长径比的研究，加载速度均为5 mm/min。该系统使用2个LED灯作为光源来保证图像清晰，通过2个互成一定角度(2α=30 °)的高速摄像机(分辨率为1 392×1 040)实时采集试件的各个变形阶段的散斑图像，并计算出全场应变和显示变形情况。后处理中，以图形化显示测量结果，便于更好地理解和分析材料的性能。RPUF的准静态劈裂的加载，如图4所示。

图4 RPUF的准静态劈裂效果Fig.4 Quasi-static splitting effect of RPUF

动态劈裂试验是在加长型分离式霍普金森压杆(SHPB)上进行，SHPB主要由气炮系统、入射杆、透射杆、吸收杆以及数据采集系统组成，试验装置示意图如图5所示。杆系直径均为 75 mm，入射杆、反射杆和透射杆的长度分别为6 000、3 500、3 000 mm，杆系材料为45钢，密度为7 800 kg/m3，弹性模量为210 GPa。入射杆和透射杆上应变片的贴片位置分别距离试件端面为2.20 m和1.03 m，整个实验中应变片位置无变化。在应变率效应研究中，试验加载气压份分别为0.24、0.28、0.32 MPa；关于试件长径比的研究，加载气压均为0.26 MPa。

图5 SHPB装置示意图Fig.5 SHPB device diagram

由于RPUF属于吸能材料，且透射杆上信号较弱，电阻应变片不能很好地采集到信号，因此透射杆均采用灵敏度系数为110，阻值为120 Ω的半导体应变片，而入射杆采用的是灵敏度系数为2.03，阻值为120 Ω的电阻应变片，RPUF试件的动态劈裂加载如图6所示。

图6 RPUF的动态劈裂Fig.6 Dynamic split of RPUF

1.5 试验原理

1.5.1 静态劈裂实验原理

一般而言，脆性材料Griffith破坏准则的等效应力σG是以最大主应力σ1和最小主应力σ3的组合情况进行计算的，如式(1)所示：

(1)

其中，规定主应力符号以拉为正，压为负，且σ1≥σ2≥σ3。RPUF的抗拉强度为σT，当σG≥σT时材料破坏。巴西圆盘劈裂试件的受力分析，如图7所示。通过求解，可以得到直径上任意一点处的弹性力学解：

(2)

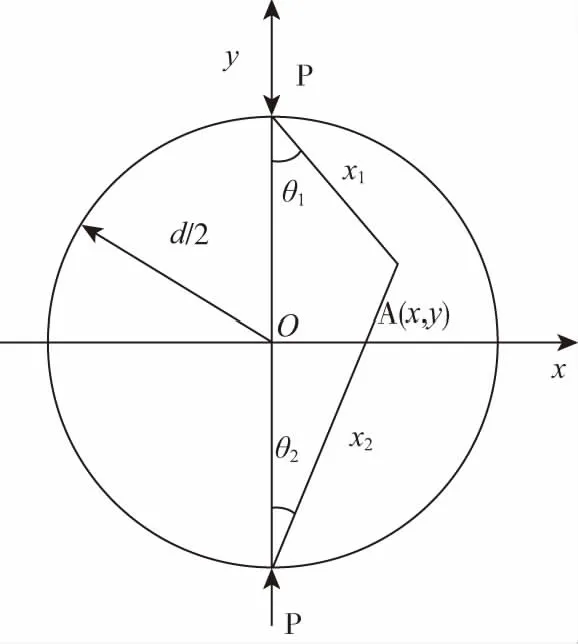
图7 巴西圆盘劈裂的弹性力学模型Fig.7 Elastic mechanics model of Brazilian disc split

又由于：

(3)

屈嘉[8]从理论上已经证明了在巴西圆盘准静态劈裂试验中，试件最先是从圆心处开始起裂；文献[9]也用精细的有限元分析证明，只有当平台对应的加载角2α≥20 °时才能根据Griffith强度准则保证中心起裂条件。在圆心处有r1=r2=d/2，θ1=θ2=0，通过式(2)计算得到的σx、σy和τxy，再将这3个应力分量带入式(3)得到：

(4)

按照弹性力学中力的方向规定，式(4)中的P为负，故式中的σ1为正，σ3为负。由此式可知，对于RPUF的材料性质，其抗压强度远大于抗拉强度，即抗压强度是抗拉强度的3倍。因此，通常认为试件是受拉破坏而非受压破坏，将式(4)中的P替换为-Pt并带入式(1)，可得到巴西圆盘劈裂抗拉强度的计算公式：

(5)

对于平台巴西圆盘，其抗拉强度需在式(5)加入一个修正系数k[10]，即：

(6)

式中σT——试件的抗拉强度

Pt——试件破坏时的压力载荷

d——试件直径

h——试件的厚度

k——与平台尺度有关的系数，当加载角2α=20 °时，k=0.96

因此，平台巴西圆盘的劈拉强度为：

(7)

1.5.2 动态劈裂实验原理

由于RPUF属于高硬度的高密度泡沫材料，因此可以考虑将岩石动态劈裂试验方法应用于此。利用霍普金森压杆(SHPB)装置进行动态劈裂，在高压气体被释放的瞬间，驱动撞击杆(子弹)加速运动撞击入射杆时，入射杆中产生向右的应力脉冲，即入射波；应力脉冲到达入射杆右端面时，一部分反射会入射杆中形成反射波，另外一部分继续向前传播，推动试件高速变形，透过试件的应力脉冲进入透射杆形成透射波。压杆中的传播的应力脉冲信号，分别由粘在入射杆和透射杆上的应变片采集，并由超动态应变仪转变为电信号，然后再由瞬态波形存储器转换为离散信号存储起来，显示在示波器中。

其中，试件与入射杆、反射杆胶粘的两端的载荷P1、P2分别为：

P1=A0E0[εi(t)+εr(t)]

(8)

P2=A0E0εt(t)

(9)

(10)

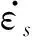
(11)

(12)

(13)

其中，εi(t)、εr(t)、εt(t)分别为电压信号转换之后的入射应变、反射应变和透射应变；C0、A0和E0分别为压杆的纵向波速、横截面积和弹性模量，As和Ls分别为试件的横截面积和长度。

对于垫条式的平台巴西圆盘，当平台中心角为2α=20 °时，其抗拉强度计算仍需添加修正系数k，即其抗拉强度计算公式为：

(14)

2 结果与讨论

2.1 静态劈裂试验结果与分析

针对RPUF的准静态劈裂，本文考虑了密度、应变率、长径比3种因素对其拉伸性能的影响，主要从应变率效应和尺寸效应2个方面进行研究。

2.1.1 RPUF准静态劈裂的应变率效应

试验试件尺寸均为φ74 mm×37 mm，密度分别为0.54 g/cm3和0.62 g/cm3的2种高密度材料；加载速率分别为2、10、20、30 mm/min，对应的应变率分别为9.00×10-4、4.50×10-3、9.00×10-3和1.35×10-2s-1，2种不同高密度的RPUF准静态劈裂力学性能参数分别表1和表2所示。

表1 低密度RPUF准静态劈裂的力学性能参数Tab.1 Quasi-static splitting mechanical properties of low density RPUF

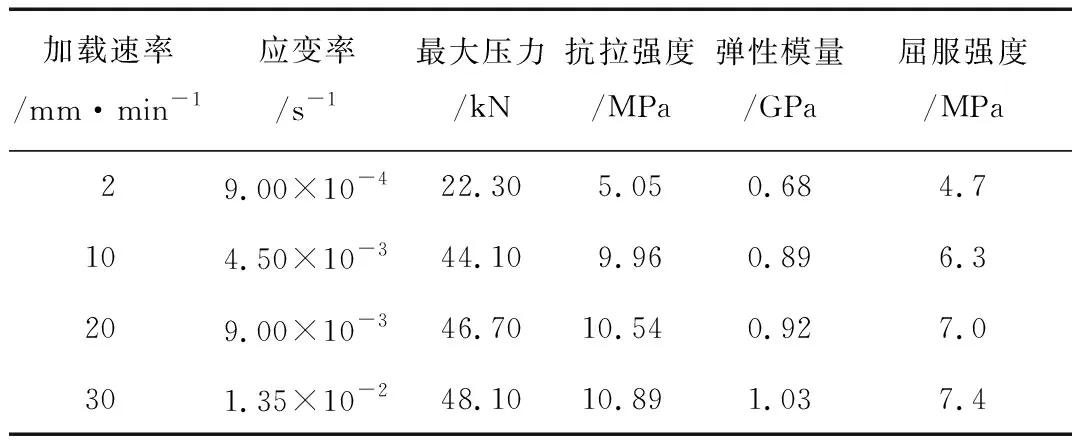
表2 高密度RPUF准静态劈裂力学性能参数Tab.2 Quasi-static splitting mechanical properties of high density RPUF

从表中数据可以看出，RPUF的抗拉强度随着加载应变率的增大而提高，而且与密度有一定关系，即密度越大，其抗拉强度也相对较大。然而，对于较高密度材料，当应变率达到一定值后，其抗拉强度的变化不再明显。这是由于RPUF的密度越高，则脆性越大的缘故，表现为脆性破坏。另外，材料的弹性模量、屈服强度也随加载应变率的增加而有增大的趋势，只是高密度材料的弹性模量和屈服强度要相对低密度有一定的提高。由此可见，虽然高密、低密度RPUF材料均表现出一定的应变率效应，但是低密度材料相对高密度材料具有较强的率敏感性。

从图8中可以看出，RPUF的加载过程主要有弹性变形和塑性屈服2个阶段。在弹性变形阶段，载荷随加载位移的增大而呈线性增加；在塑性屈服阶段，试件的抗拉能力随着加载速率的变化开始发生明显的分歧，即加载速率越大，RPUF的抗拉承载能力就越大，也即抗拉强度越大，故表现出明显的应变率效应。此外，RPUF的密度对其拉伸性能也具有重要影响，其抗拉强度有随材料密度的增大而增加的趋势。

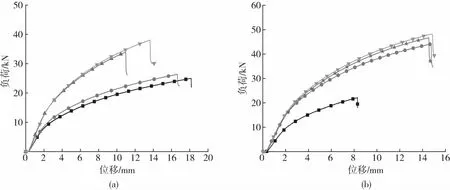
加载速率/mm·min-1：■—2 ●—10 ★—20 ▼—30ρ/g·cm-3:(a)0.54 (b)0.62图8 不同加载速率下的负荷 - 位移曲线Fig.8 Load-displacement curves at different loading rates

2.1.2 RPUF准静态劈裂的尺寸效应

试验材料密度为ρ=0.62 g/cm3，加载速率均为5 mm/min，试件长径比分别为0.4、0.5和0.8(尺寸分别为Φ50 mm×20 mm、Φ50 mm×25 mm和Φ50 mm×40 mm)。不同长径比劈裂拉伸的力学性能参数如表3所示。显然，由试验结果可以看出，抗拉强度、弹性模量均随试件长径比的增大而有降低的趋势。实际上，这也验证了试件与压盘的接触面积和抗拉强度的本质关系，因为长径比越大，即厚度方向增大，使得其与压盘的接触面积也就越大，从而使得单位面积上的应力减弱，故抗拉强度降低。平均抗拉强度与长径比的关系，如图9所示。

表3 不同长径比劈裂拉伸的力学性能参数Tab.3 Tensil mechanical properties of splits at different aspect ratios

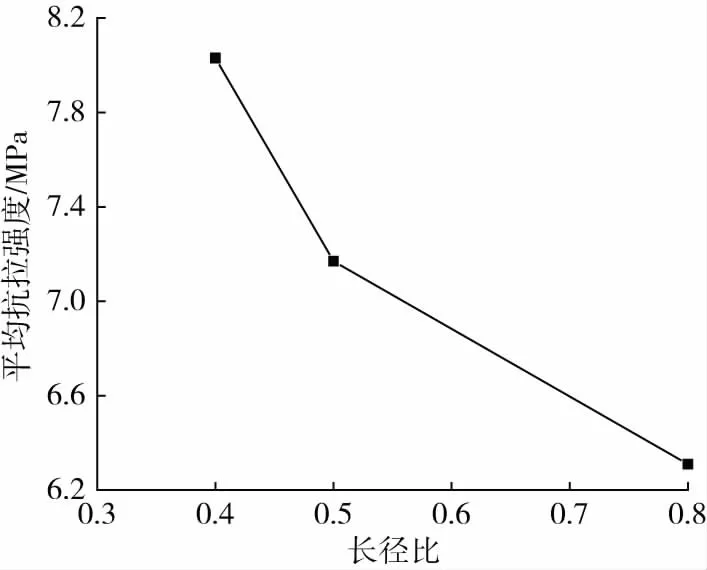
图9 平均抗拉强度与长径比的关系Fig.9 Relationship between average tensile strength and aspect ratios

2.2 准静态劈裂的结构破坏分析

(a)阶段1 (b)阶段2 (c)阶段3 (d)阶段4 (e)阶段5 (f)临界图10 x方向的应变场演化Fig.10 Strain field evolution in x direction

(a)阶段1 (b)阶段2 (c)阶段3 (d)阶段4 (e)阶段5 (f)临界图11 y方向的应变场演化Fig.11 Strain field evolution in y direction

从图10和图11中可以看出，x方向上的应变主要表现为拉伸应变，y方向主要表现为压缩应变。其中，最大拉应变为20.34 %，最大压应变为14.01 %，但无论是拉应变还是压应变，最终临界状态的最大变形区域还主要集中于试件的中心区域。可以明显看到，x方向的最大拉伸应变，由试件中心逐渐向左右两端扩展，最终导致试件拉伸失效；相反，y方向的最大压缩应变是从试件上下两端逐渐趋向中心区域，最终贯穿了试件的上下两端。

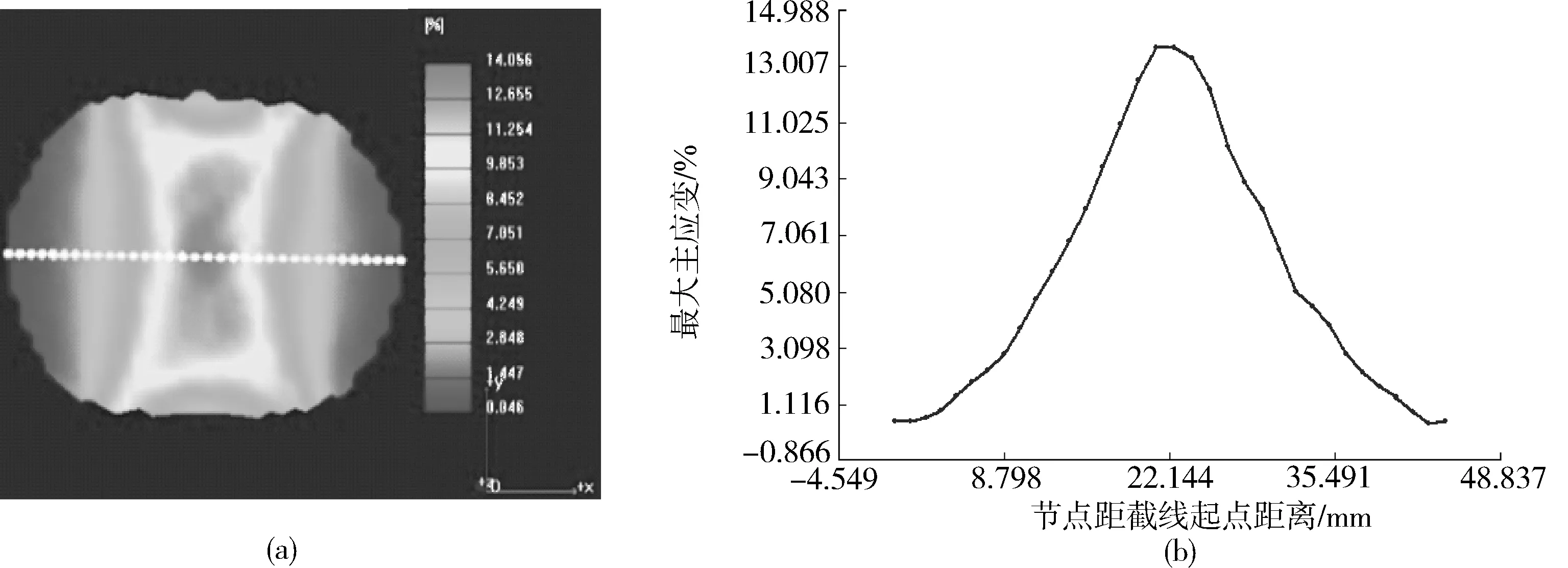
(a)x方向临界状态的最大主应变云图 (b)x方向临界状态的最大主应变 - 节点距曲线图13 x方向临界状态的最大主应变Fig.13 The maximum major strain of the critical state in x direction

图12为RPUF的最大主应变场演化过程，最大主应变的演化过程与y方向上的应变场演化过程略有相似之处，均是由试件的上下两端同时缓慢地向试件中心并贯穿试件的整个纵向区域，最终向中心部位靠拢，达到临界破坏状态。此时的试件既在x方向达到最大拉应变，且在y方向达到最大压应变。虽然在加载过程中既承受x方向的拉应力，又承受y方向的压应力，但由于抗拉强度要远小于抗压强度，因此x方向的拉应力最先达到承载极限而导致试件拉伸失效。x方向、y方向临界状态的最大主应变与节点距之间的关系分别如图13和图14所示。

(a)阶段1 (b)阶段2 (c)阶段3 (d)阶段4 (e)阶段5 (f)临界图12 最大主应变场的演化图12 Evolution of the maximum major strain field

2.3 动态劈裂试验结果

(a)y方向临界状态的最大主应变云图 (b)y方向临界状态的最大主应变 - 节点距曲线图14 y方向临界状态的最大主应变Fig.14 The maximum major strain of the critical state in y direction

图15为RPUF试件在SHPB动态劈裂试验中的典型波形。从图中可以明显看到，透射波波形要远小于入射波、反射波的波形，这是由于试件与压杆的端面相切，接触面积较小，且试件波阻抗小于压杆的波阻抗，使得大部分应力波被反射，导致透射杆上的信号比较少。为了较少端面的摩擦效应，试验前在试件与压杆接触端面涂有适量的凡士林。

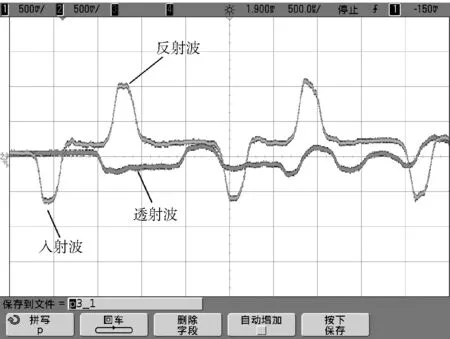
图15 RPUF的动态劈裂的典型波形Fig.15 A original waveform of dynamic split of RPUF

此外，由于RPUF为吸能缓冲材料，在加载过程中，试件端面的平台被挤压变形，即与压杆的接触面积会增大，使得透射波波形峰值呈现平台。本次RPUF的动态劈裂拉伸试验，主要考虑长径比和应变率2种因素对其间接拉伸性能的影响，即不同应变率、长径比下RPUF的动态劈裂拉伸性能参数分别如表4、表5所示。

表4 不同应变率下RPUF的动态劈裂拉伸性能参数Tab.4 Dynamic split tensile properties of RPUF at different strain rates

表5 不同长径比下RPUF的动态劈裂拉伸性能参数Tab.5 Dynamic split tensile properties of RPUF at different aspect ratios

2.3.1 应变率对劈拉强度的影响

(15)

式中σts——准静态劈拉强度

σtd——动静态劈拉强度

拟合曲线方程为：

y=A+Bx+Cx2

(16)

表6 DIF的拟合参数值Tab.6 Fitting parameter values of DIF

图16为RPUF的DIF值与平均应变率的关系，从图中可以看出，DIF值随应变率的增大而明显升高且呈非线性增长的趋势，这表明RPUF材料具有较强的率敏感性。但随着应变率的增大，DIF值的增长率逐渐变缓。一般认为，材料强度的增强主要是由于随着加载应变率的增大，材料在破坏时内部泡孔壁裂纹来不及充分扩展，在惯性力的作用下导致材料失效，而且应变率越高，惯性力越大，材料破坏时的抗拉强度也就越高。

图16 RPUF的DIF值与平均应变率的关系Fig.16 Relationship between DIF value of RPUF and average strain rate

由于试验过程中不可避免地受到外界信号及噪声等因素的干扰，使得采集到的信号毛刺较多，故在数据处理时借助Origin9.1软件中的FFT功能对由三波法处理得到的应力 - 应变曲线进行平滑和滤波处理。另外，为了降低惯性效应对试验结果的影响，试验试件采用统一的长径比0.5，在0.24、0.28、0.32 MPa 3种不同加载气压下对长径比下进行动态劈裂试验，得到的典型应力 - 应变曲线，如图16所示。

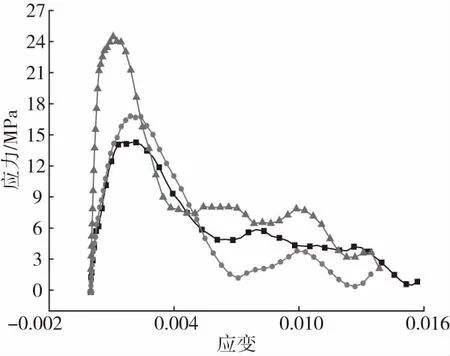
气压/MPa：■—0.24 ●—0.28 ▲—0.32图17 RPUF动态劈裂的应力 - 应变曲线Fig.17 Stress-strain curve of RPUF in dynamic split

由图17可知，RPUF的应力随着应变的增加都是先增大，而后逐渐减小，这是由于在RPUF变形的初期，内部泡孔结构受到挤压而闭合密实，为了抵抗外部的力量不得不提高自身的强度，随着冲击速度不断加大，RPUF内部的泡孔逐渐被挤压破碎且微裂纹开始不断扩大、贯通，其自由表面不断增加，传递荷载能力不断减小，因此其强度急剧下降。另外，由于RPUF具有吸能缓冲的特性且波阻抗较低，在材料失效之后，应力波需要在试件内多次来回反射才能趋于平衡。

2.3.2 长径比对平均劈拉强度的影响

为避免因加载气压过大而对试件造成多处裂纹开裂以影响试验结果的可靠性，故对长径比的研究均采用0.26 MPa的加载气压，分别对长径比为0.2、0.4、0.6和0.8这4组长径比进行了动态劈裂试验。不同长径比的应力 - 应变曲线，如图17所示。从图中可以看出，峰值应力随长径比的增大而降低，而且拉伸弹性模量也呈下降的趋势。

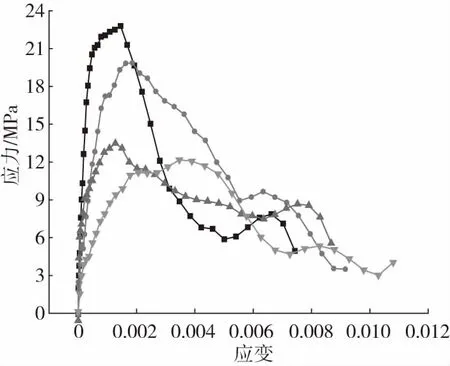
长径比：■—0.2 ●—0.4 ▲—0.6 ▼—0.8图18 不同长径比的应力 - 应变曲线Fig.18 Stress-strain curves of different aspect ratios

同静态劈裂试验一样，RPUF动态劈裂的应力 - 应变曲线也划分为3个阶段：第一阶段为RPUF的弹性变形阶段，该阶段的应力应变曲线近似为一条直线，其斜率为一定值，表现为较强的弹性特征以及较高的耐冲击强度；第二阶段为非线性弹性阶段，该阶段的曲线表现为非线性变形，进入本阶段后，在试件纵向产生拉伸载荷使得内部泡孔受拉破坏，微裂纹开始逐步扩展开来，发生了质的改变。RPUF内部的裂隙在冲击载荷作用下开始增加、贯通。当达到该阶段的最高点，即试件的峰值强度之后试件便开始发生破坏，导致应力急剧下降；第三阶段为破裂后阶段，RPUF的承载能力到达了极限后，其内部发生损伤，试件内部的微裂纹快速发展，形成了宏观断裂面。此后，其承载力随变形增大而快速下降，但试件的总应变会持续增加。

图19为长径比与平均抗拉强度之间的关系，由图可知，平均抗拉强度随长径比的增大逐渐降低。其中，长径比由0.4增大到0.6，平均抗拉强度的下降幅度最大约为28.0 %，由0.6增大到0.8下降幅度最小约为 17.7 %。这是由于在同一加载气压下，试件长径比越大(即厚度方向增大)则单位面积上的承载作用力就相对较小，反之越大。

图19 平均抗拉强度与长径比的关系Fig.19 Relationship between average tensile strength and aspect ratio

3 结论

(1)在RPUF的准静态劈裂试验中，RPUF的抗拉强度随着加载应变率的增大而提高，而且与密度有着密切关系，即材料密度越大，其抗拉强度也相对较高；对于较高密度材料，当应变率达到一定值后，其抗拉强度的变化不再明显；另外，材料的弹性模量、屈服强度也随加载应变率的增加而有增大的趋势；在RPUF尺寸效应研究中，发现RPUF的抗拉强度、弹性模量均随长径比的增大而降低；

(2)由准静态劈裂的结构破坏分析得知，在x方向主要承受拉伸载荷，y方向承受压缩载荷，并且x方向临界破坏状态的最大主应变还主要集中于试件的中心区域，随载荷的增大而逐渐增加，而最大主应变由试件中心逐渐向左右两端逐渐减小；

(3)在动态劈裂试验中，RPUF的DIF值随应变率的增大而明显升高，且呈非线性增长的趋势，这表明RPUF材料具有较强的率敏感性。但随着应变率的增大，DIF值的增长率逐渐变缓。另外，RPUF的抗拉强度峰值应力随长径比的增大而降低，而且拉伸弹性模量也呈下降的趋势。