城市轨道交通桥梁线形变化对列车运行性能的影响

秦清华

(重庆市轨道交通(集团)有限公司，重庆 401120)

城市轨道交通具有运输能力大、安全快捷和环境污染小等优点，迅速发展成为城市公共交通的重要组成部分。在城市轨道交通中高架桥梁占据着举足轻重的地位，在河道和公路的跨越方面具有很大优势，整段线路中高架桥梁往往具有十分高的比例。由于列车疲劳荷载、温度变化、混凝土收缩徐变、预应力损失、墩台差异沉降、支座老化等不利因素的影响，高架桥在长期服役过程中梁体线形将发生变化，进而影响线路的平顺性[1-3]。列车高速运行时若线路平顺性不良，则会导致列车振动加剧、轮轨力增大，旅客舒适度会受到严重影响，轨道状态不能保持稳定，甚至造成列车脱轨，影响列车的运行安全。桥梁线形的变化主要表现为桥墩沉降和主梁的下挠或上拱。研究表明，桥墩发生不均匀沉降后铺设在桥面上的轨道结构会随之发生变形，线路平顺性变差，高速列车通过该区域时，其平稳性和安全性将受到影响[4-6]。同样，主梁产生下挠或上拱变形时，高速列车与桥梁间的耦合振动也会加剧[7-9]。城市轨道交通桥梁结构的刚度与高速铁路有一定差异，其车辆性能与运行速度与高速铁路车辆也有较大差距，城市轨道交通与高速铁路的车-桥耦合振动特性必然有所不同。然而，目前针对城市轨道交通高架桥梁线形变化对列车运行性能影响的研究相对较少，因此有必要对此开展研究。

本文将多体动力学与有限元方法结合起来进行计算。采用有限元方法建立桥梁模型，而包含复杂轮轨关系的车辆模型则通过多体动力学进行分析，二者的数据交换在包含离散信息点的轮轨接触面上进行，从而构建联合仿真平台，实现车-桥系统的耦合振动分析。针对城市轨道交通高架桥梁，研究了桥墩沉降和主梁下挠及上拱对列车安全性和舒适性的影响，并提出了相应的建议限值，为桥梁结构的优化设计提供参考。

1 车-桥耦合振动分析方法

1.1 车辆模型

采用地铁B型车，车辆模型包括1个车体、2个转向架和4个轮对共计7个刚体，并通过一系弹簧、二系弹簧、减振器、抗侧滚扭杆等构件进行连接，采用多体动力学软件SIMPACK建立动车和拖车的仿真模型[10-12]。车辆模型独立铰为34个，约束为8个，总计42个自由度。列车系统模型考虑了轮轨接触几何非线性、轮轨蠕滑力非线性和一、二系弹簧的非线性。列车采用6车编组，编组方式为TC+MP+M+M+MP+TC，列车三维模型如图1所示。

轮轨接触关系主要包括轮轨间的几何相容条件和轮轨相互作用力2个方面。车辆模型采用LM coach型车轮踏面，并配以我国60 kg/m钢轨。轮轨接触的几何关系中名义滚动圆半径为420 mm，轨底坡为1/40，轨距为 1 435 mm。轮轨相互作用力主要包括轮轨间的法向力和蠕滑力，轮轨法向力通过Hertz非线性弹性接触进行计算，蠕滑力则通过Kalker简化理论——FASTSIM算法计算。随机不平顺采用美国六级谱，轨道激励包括左右轮轨的横向和垂向不平顺，如图2所示，并考虑了速度和加速度激扰。

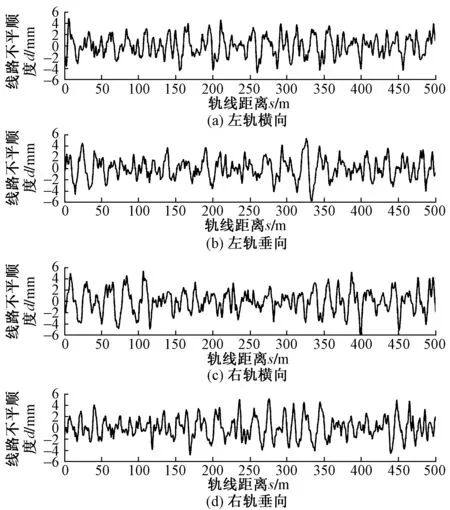
图2 美国六级谱轨道激励

1.2 桥梁模型

以重庆市某地铁高架5跨简支梁桥为研究对象，桥梁跨度为30 m，3个桥墩高度为18 m，主梁和桥墩尺寸如图3所示。

采用通用有限元软件ANSYS对桥梁进行建模，有限元模型如图4所示。通过模态分析得到桥梁的前10阶自振频率，见表1。图5给出了前10阶的振型。为提高计算效率，采用经典的Guyan缩减法对桥梁结构进行子结构分析。其分析过程分为生成部分、使用部分和扩展部分，如图6所示。

1.3 车-桥耦合方法

SIMPACK的前处理程序调用桥梁的质量矩阵、刚度矩阵、节点坐标等信息，将桥梁作为弹性体耦合集成到多体系统中。弹性体在多体动力学中的建模方法是引入浮动坐标系，弹性体的运动通过浮动坐标系的运动和相对于浮动坐标系的弹性变形叠加得到。其中，浮动坐标系的运动利用广义笛卡尔坐标表示，弹性变形则可通过相对较少的模态坐标处理，即采用模态叠加法考虑。弹性体桥梁在多体系统中的运动可通过1个惯性坐标系和3个浮动坐标系进行描述[13]。

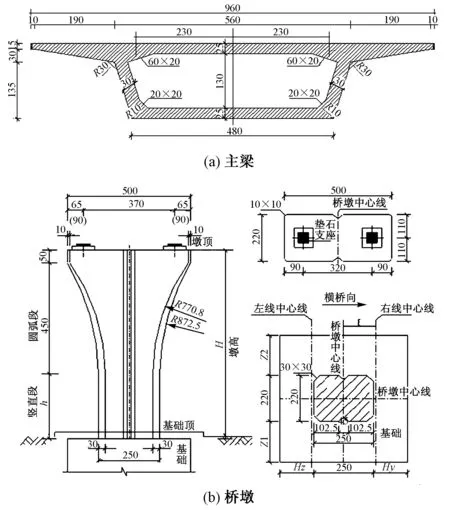
图3 主梁及桥墩尺寸(单位：cm)

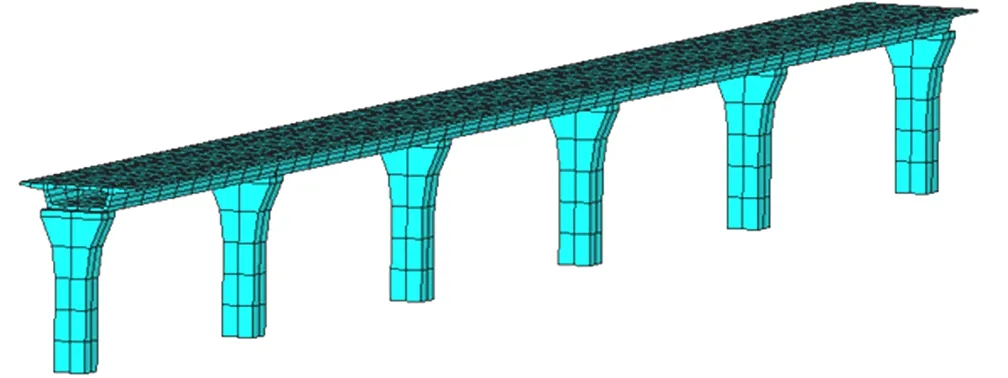
图4 桥梁有限元模型

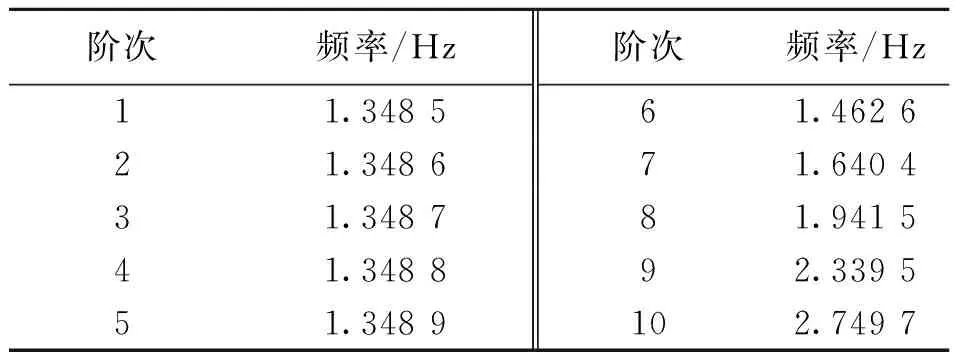
表1 桥梁自振频率

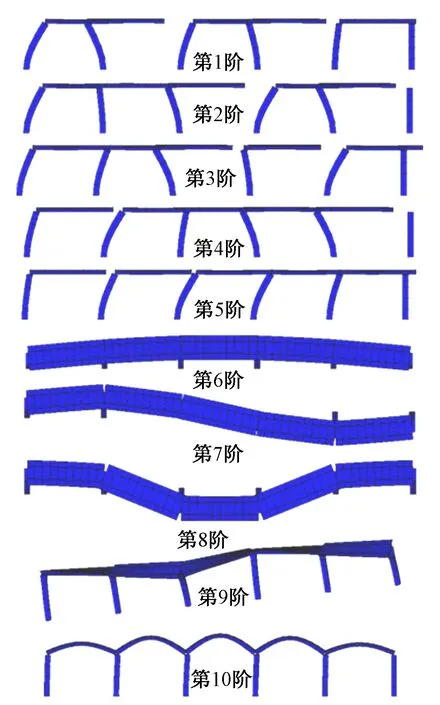
图5 桥梁前10阶振型

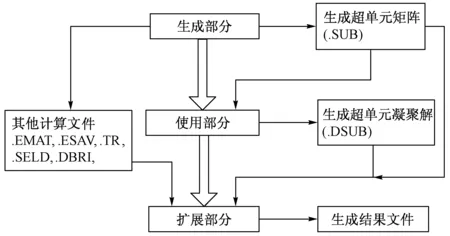
图6 子结构分析流程

通过约束和力元对桥梁和轨道进行连接，使力和位移得到传递，从而实现车-桥耦合振动，车-桥系统的耦合振动仿真模型如图7所示。

图7 车-桥系统耦合振动仿真模型

2 线形变化对车-桥系统动力特性的影响

参照日本规范，采用图8所示半波正弦曲线模拟主梁变形(下挠/上拱)[14]。将此静态变形与随机不平顺谱进行叠加，得到叠加不平顺，对车辆模型进行激励。桥墩沉降则以位移边界作用于墩底，假定4号桥墩发生沉降，如图9所示。在此基础上，分别计算了车速为80，100，120 km/h时不同桥墩沉降量及主梁变形量下车辆动力响应，计算结果如图10—图12所示。图13给出了车速为120 km/h时，桥梁无线形变化、桥墩沉降50 mm、主梁下挠30 mm 和主梁上拱30 mm 4种情况下车辆动力响应时程曲线。图14给出了车速为120 km/h时，桥墩沉降50 mm、主梁下挠30 mm和主梁上拱30 mm 3种情况下主梁竖向位移时程曲线。

图8 简支梁半波正弦曲线模型

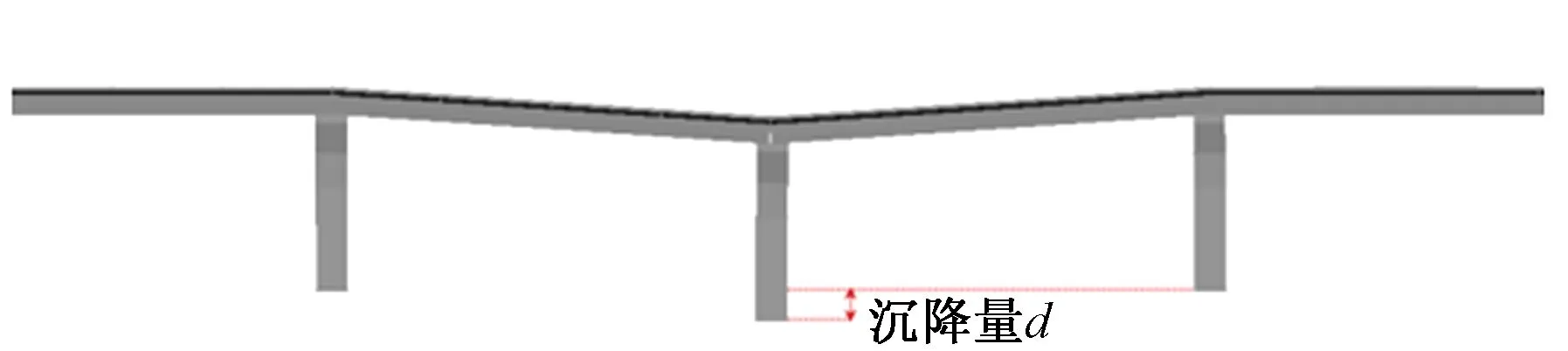
图9 桥墩沉降示意

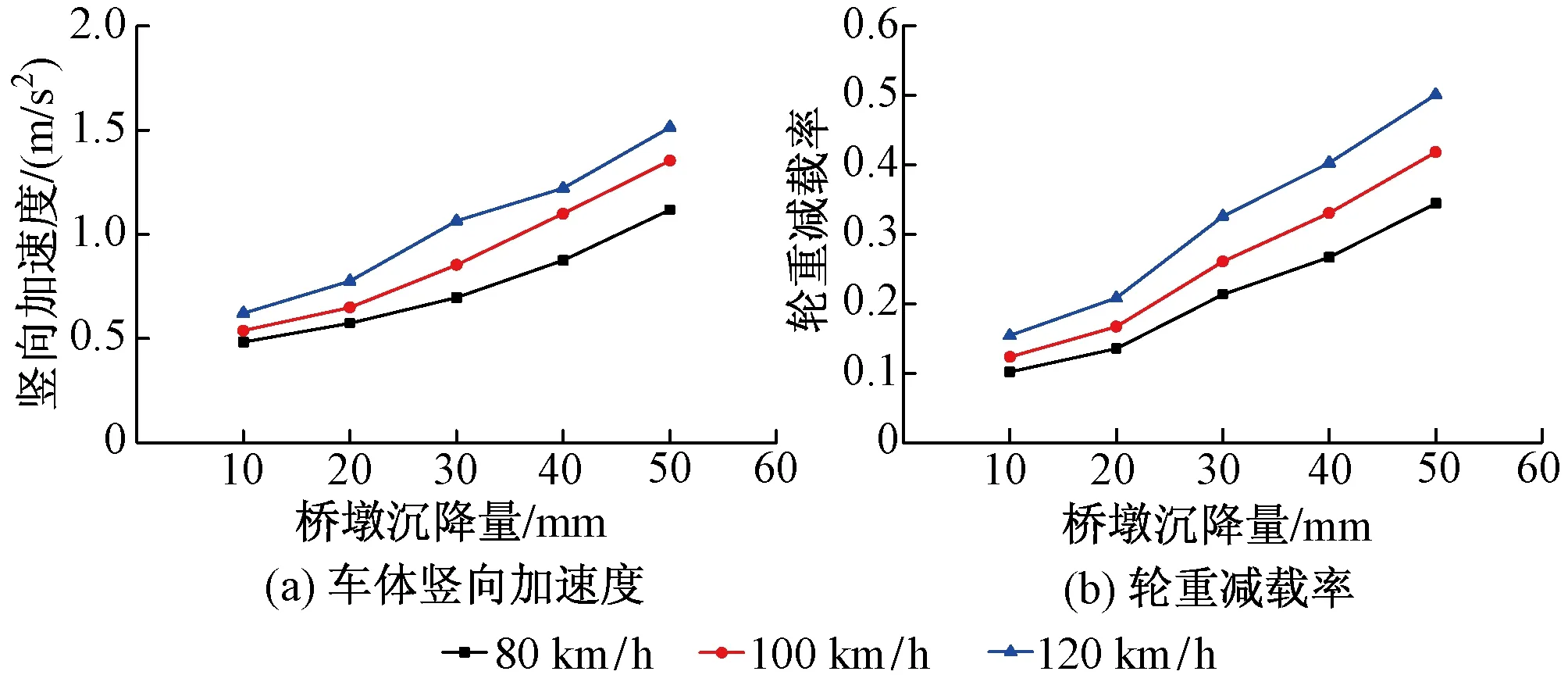
图10 不同桥墩沉降量时车辆动力响应

图11 不同主梁下挠量时车辆动力响应

图12 不同主梁上拱量时车辆动力响应

图13 车辆动力响应时程曲线

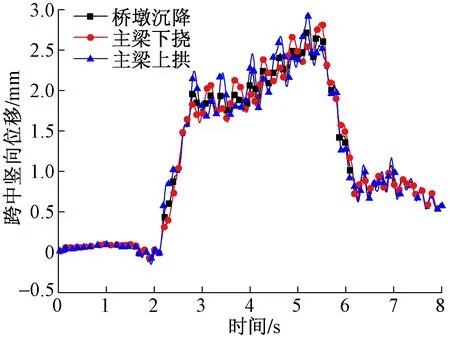
图14 主梁竖向位移时程曲线

由图10—图14可以看出：

1)桥墩发生沉降后，列车在未沉降区车体竖向加速度和轮重减载率与未发生沉降时相近，列车经过沉降区时车体竖向加速度和轮重减载率均明显增大，且在沉降墩处出现最大值。车速相同时，随着沉降量的增加车体竖向加速度和轮重减载率均不断增大，沉降量每增加10 mm车体竖向加速度最大可增加37.2%，轮重减载率最大可增加57.5%。在相同的沉降量下，车体竖向加速度和轮重减载率随车速的增大而增大，且沉降量较大时不同车速间列车动力特性的差距更加明显。

2)主梁发生下挠或上拱变形时，列车的车体竖向加速度和轮重减载率均明显增大。车速一定时，车体竖向加速度及轮重减载率均随主梁变形量的增大而增大。下挠量每增加5 mm车体竖向加速度最大可增加49.5%，轮重减载率最大可增加47.1%;上拱量每增加5 mm车体竖向加速度最大可增加48.3%，轮重减载率最大可增加43.8%。主梁变形一定时，车体竖向加速度和轮重减载率均随车速的增大而增大，与上拱相比，下挠对列车的动力特性更加不利，这是由于列车上桥后车辆荷载可以平衡一部分上挠量，而车辆荷载会加剧主梁的下挠。

3)车速不高于120 km/h，沉降量在50 mm以内时，列车的轮重减载率均小于0.6，满足规范要求[15]，行车安全性可以得到保证;而车体竖向加速度最大为1.51 m/s2,不能满足规范要求的1.3 m/s2[15]，无法完全保障乘客的舒适性。同样，车速不高于120 km/h，主梁下挠或上拱变形量在30 mm以内时，列车的轮重减载率均满足要求，但车体竖向加速度不能完全满足要求。

3 线形变化限值的确定

以轮重减载率0.6为安全性评价指标，以车体加速度1.3 m/s2为舒适性评价指标，基于车-桥耦合振动方法，通过改变主梁的竖向变形量和桥墩的沉降量，不断试算使车体加速度和轮重减载率分别达到限值，从而确定运营舒适性限值和行车安全性限值，计算结果如表2所示。

表2 桥梁线形变化限值

由表2可知：列车以低于120 km/h速度通过 30 m跨度的简支梁桥时，桥墩沉降的运营舒适性限值为47 mm，行车安全性限值为63 mm；主梁下挠的运营舒适性限值为19 mm，行车安全性限值为32 mm；主梁上拱的运营舒适性限值为24 mm，行车安全性限值为35 mm。

4 结论

针对城市轨道交通高架桥梁线形变化问题，以30 m 跨简支梁高架桥为研究对象，通过有限元软件ANSYS和多体动力学软件SIMPACK分别建立了桥梁的有限元模型及多体动力学模型，并通过子结构分析及刚柔耦合技术，实现二者的联合仿真，建立了车-桥耦合联合仿真模型。以车体加速度为舒适度评价指标，以轮重减载率作为安全性评价指标，研究了桥墩沉降和主梁下挠及上拱对列车动力特性的影响，主要得出以下结论：

1)桥墩发生沉降后，列车在未沉降区车体竖向加速度和轮重减载率与未发生沉降时相近，列车经过沉降区时车体竖向加速度和轮重减载率均明显增大，且在沉降墩处出现最大值。车体竖向加速度和轮重减载率均随桥墩沉降量及车速的增大而增大。

2)主梁发生下挠或上拱变形时，列车的车体竖向加速度和轮重减载率均明显增大，与上拱相比，下挠对列车的动力特性更加不利。车体竖向加速度和轮重减载率均随主梁变形量及车速的增大而增大。

3)城市轨道交通车辆以低于120 km/h速度通过30 m跨高架桥梁时，桥墩沉降的运营舒适性限值为47 mm，行车安全性限值为63 mm；主梁下挠的运营舒适性限值为19 mm，行车安全性限值为32 mm；主梁上拱的运营舒适性限值为24 mm，行车安全性限值为35 mm。