运营高速铁路路基变形段轨道几何状态自动监测技术

高至飞

(广州铁路科技开发有限公司，广东 广州 510100)

路基病害、涉及铁路的工程施工等引起运营高速铁路路基变形，造成轨道几何状态变化时，需对线路几何状态进行测量。这类问题的明显特征是受影响区域相对集中，轨道几何状态变化量较大。目前，对既有铁路轨道几何状态监测主要采用人工测量的方法[1]。由于高速铁路行车速度快、行车密度大、线路全封闭，人工测量的方法只能在晚上天窗点进行，无法实时监测线路的运营状况。

本文探讨如何在高速铁路路基变形段对轨道几何状态变化进行实时自动监测。基本思路是在轨道(轨腰)上安装专用棱镜，组建基于自动全站仪的轨道几何状态实时自动监测系统，连续监测高程、平面位置、轨距、水平、高低、轨向等轨道几何参数变化情况[2]，实现数据自动采集、计算、传输和报警，以保证高速铁路运营安全。

1 轨道几何状态自动监测技术

1.1 轨道几何状态自动监测原理

本文采用相对变化量的方法计算轨道几何状态参数[3-4]。轨道几何状态变化量，采用带自动监测系统的极坐标法进行测量。首先在监测范围的轨腰上安装专用棱镜，人工利用安博格小车测出监测范围内轨道几何状态参数作为初始值，然后通过自动全站仪测量出轨道上各测点的坐标，用每次测量值与前次测量值相减即得到本次变化量。用每次测值与初始测量值相减即得到累计变化量，经几何关系换算得到高程、平面位置以及轨距、水平、高低、轨向、扭曲及轨距变化率的本次及累计变化量。累计变化量与人工测得的初始值相加即为当前的轨道几何状态。

假设某段轨道上有A(xA,yA,hA)，B(xB,yB,hB)，C(xC,yC,hC)及相对应另一条轨道上的A′(xA′,yA′,hA′)，B′(xB′,yB′,hB′)，C′(xC′,yC′,hC′)6个点，式中(x，y，h)指测点的空间坐标。由安博格小车测出的几个测点(断面)的轨道几何状态初始值分别为高程H0，平面位置S0，水平P0，轨距G0，根据上述计算原理和轨道几何状态参数的基本定义来计算各个参数。

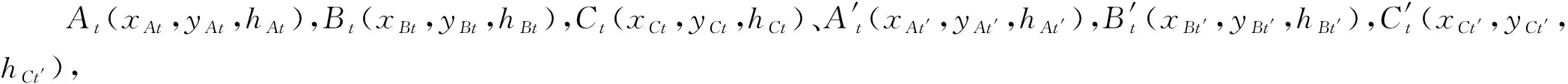
则A点时刻t的轨面高程HAt

HAt=HA0+(hAt-hA)

(1)

式中：HA0为A点的初始高程;hAt为A点时刻t的竖向坐标。

以A,B为基点，计算轨道点C到AB直线的距离。C点到AB直线的距离初始值LC0为

(2)

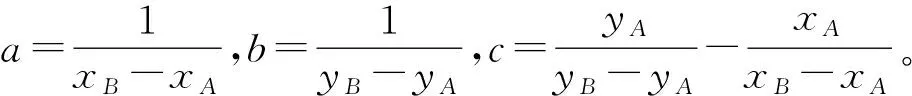
C点t时刻的平面位置SCt为

SCt=SC0+(LCt-LC0)

(3)

式中：SC0为C点初始平面位置；LCt为t时刻C点到AB直线的距离。

A和A′两点初始距离LAA′为

(4)

AA′断面t时刻的轨距GAtA′t为

(5)

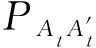
(6)

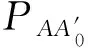
得到外部轨道几何状态4个参数后，根据内部轨道几何状态参数定义可以分别求得内部轨道几何状态参数,故本文中只讨论上述4个参数。

1.2 误差分析

(7)

式中，mh为h坐标的中误差。

平面位置中误差m平面位置为

(8)

式中：mx为x坐标的中误差，my为y坐标的中误差。

水平中误差m水平为

m水平=2m平面位置

(9)

轨距中误差m轨距为

(10)

以2测回的测量条件下对上述轨道几何状态参数进行误差分析，确定是否满足使用要求。

监测仪器采用徕卡-TS30型全站仪，该仪器测角精度为0.5″，测距精度为0.6 mm+每1 km增加1 mm，现场测量最大斜距D=100 m，最大竖直角θ=-10°，则最大天顶距Z=100°，考虑水平角β=0.01°，β=89.99°，β=45°，测站和监测点均强制对中，不考虑对中误差。

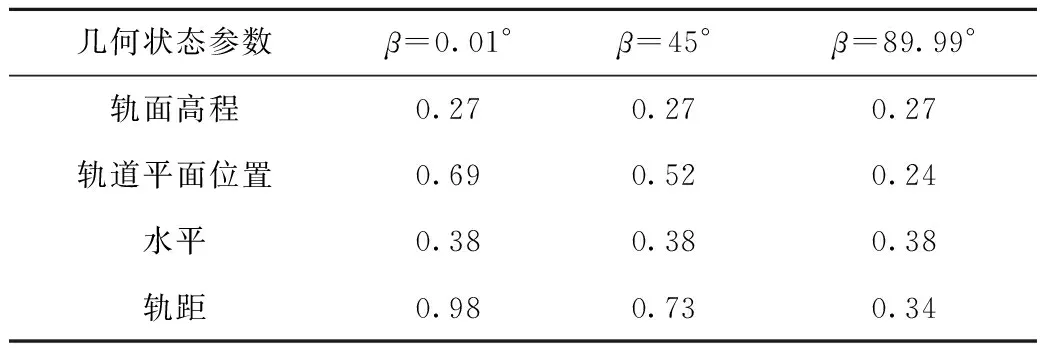
表1 t时刻轨道几何状态各参数的中误差 mm

由表1可知:在2测回的测量条件下t时刻轨道几何状态参数轨面高程、轨道平面位置、水平、轨距中误差皆在1 mm以内，可以满足对轨道几何状态参数的测量要求。

相信大多数朋友已经对全画幅数码相机的技术特点与发展历程比较熟悉了，今天我们就从一些重要节点入手，来看看全画幅机型是如何一路走来发展至巅峰的。

2 高速铁路轨道几何状态自动监测技术可靠性对比分析

对比机器人和安博格小车的实测数据，分析两者所测得区段轨道几何状态参数的相关性和二者差值分布情况，试验选取2016年8月5日的数据进行对比分析。

对机器人与安博格小车所测轨道几何状态数据作相关性及显著性分析，采用SPSS软件计算结果见表2。可知：在相同的试验日期，机器人与安博格小车所测轨道高程、平面位置、水平和轨距在试验段的分布曲线形态基本一致，高度相关。

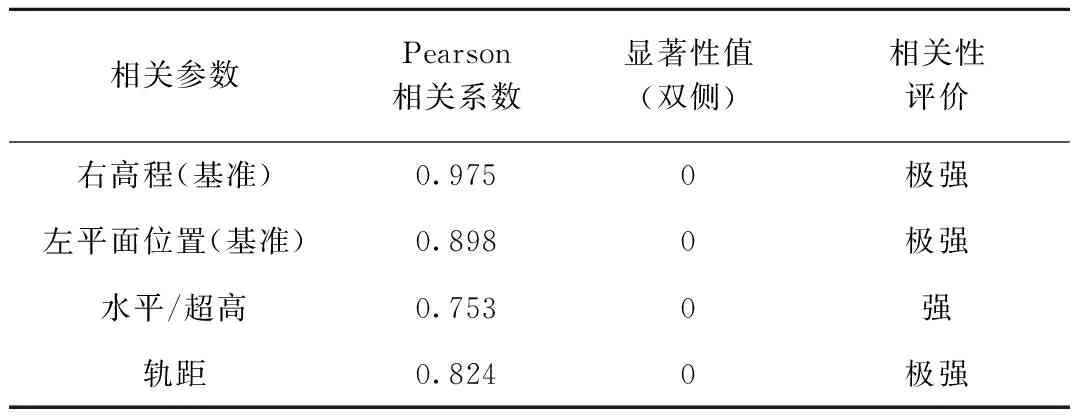
表2 2种方法测值的Pearson相关系数和显著性值

在相同的试验日期，机器人和安博格小车对轨道高程、平面位置、水平、轨距的测量差值按正态分布规律来统计(见表3)，越靠近差值样本均值，分布频数越高，越远离均值，分布频数越低。从表3可知：机器人和安博格小车所测轨道高程、平面位置、水平、轨距差值均值分别为-0.9,0.5,0.5,-0.1 mm，均小于1 mm；在(μ-2σ)～(μ+2σ)分布数量分别达到了28,29,28,30，分别占总样本数31的90%,94%,90%,97%。可见，机器人和安博格小车对轨道高程、平面位置、水平、轨距的测量差值不大且较为集中。

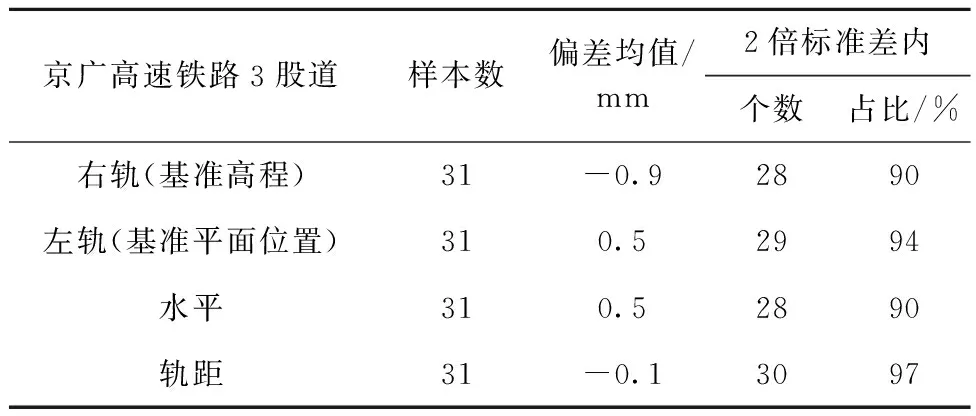
表3 2种方法所测轨道几何参数差值正态分布统计

综上所述，机器人与安博格小车测得的轨道几何状态相关性高，差值不大且离散性小。由此可见机器人测得的轨道几何状态是可靠的，用机器人代替安博格小车在固定区段进行轨道几何状态的自动监测是可行的。

3 高速铁路轨道几何状态自动监测技术在工程中的应用

3.1 工程概况

广州市轨道交通9号线工程广州北—花城路区间隧道在出广州北站后下穿京广高速铁路4条股道及两侧站台(穿越里程为K2247+510—K2247+550)，下穿铁路站台及股道宽度共约60 m[6-7]。此项目为国内首例地铁在灰岩、砂层地区以浅埋隧道方式下穿高速铁路路基施工，工程风险极大，为了确保施工中京广高速铁路安全运营，需要连续监测加固及隧道穿越施工时引起的轨道几何状态变化情况。

3.2 监测方案

对京广高速铁路3股道及4股道进行监测，监测频率为3次/d。轨道几何状态自动监测系统硬件主要为测量机器人和特制棱镜。轨道几何状态监测点以专用棱镜作为观测标志，棱镜具体尺寸为2 cm×2 cm×1 cm，外壳材料为工程塑料，棱镜用环氧树脂系胶结剂粘结在轨道(轨腰)上，间隔1 m布置，并面向观测基站。

3.3 施工过程中监测试验及数据分析

轨道几何参数的符号取值与安博格小车一致，因下一段曲线为右转曲线故轨面高程右轨为基准轨，轨道平面位置以高速铁路3股道左轨为基准轨。轨道平面实际位置位于设计位置左侧时，偏差为负；平面实际位置位于设计位置右侧时，偏差为正。轨面实际高程高于设计高程时，偏差为正；低于设计高程时，偏差为负。左轨高于右轨，则超高为正值；左轨低于右轨，则超高为负值。实际轨距大于标准轨距时轨距偏差为正，反之为负[8]。

由于K2247+526里程位置处于竖向沉降较大区域，故选取其作代表性的断面进行分析。

3.3.1 高程

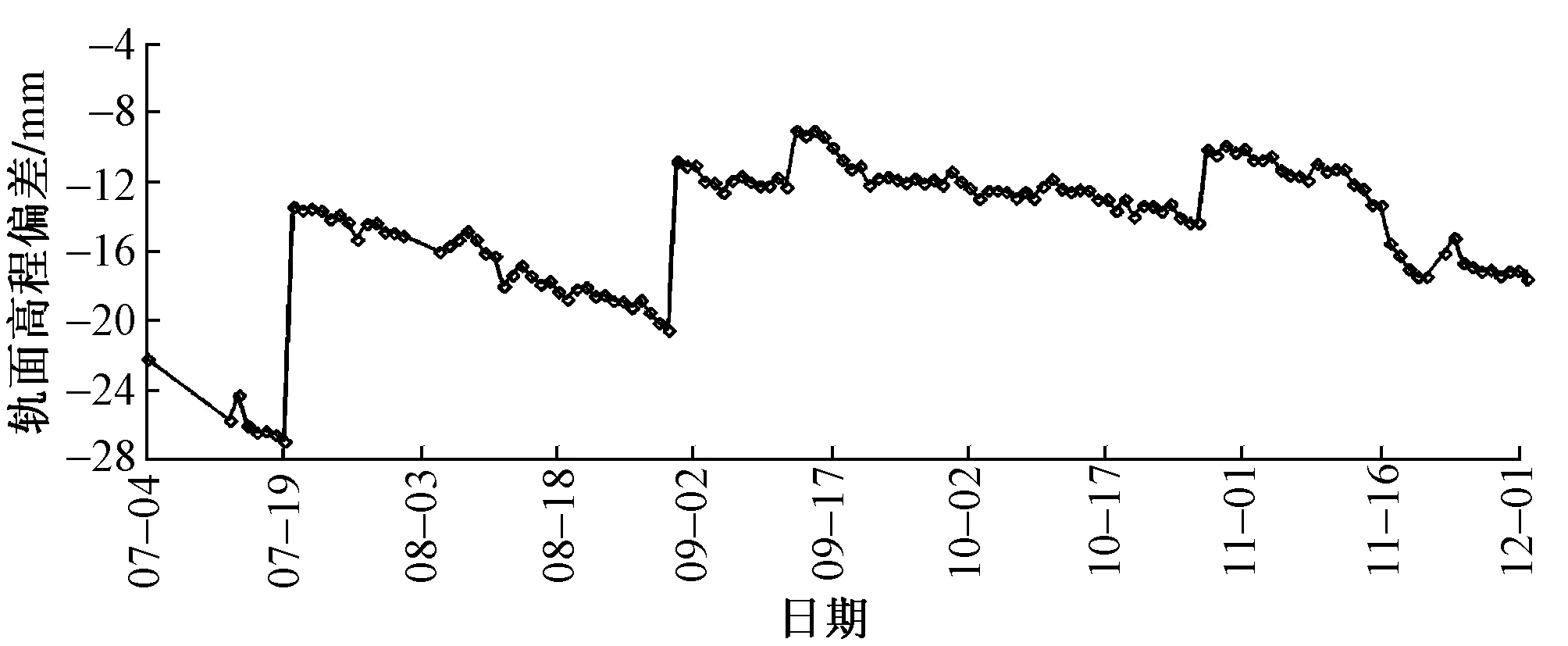
图1 K2247+526断面轨面高程偏差随时间变化曲线(2016年)

2016年K2247+526断面轨面高程偏差随时间变化见曲线图1。可知：7月4—19日轨面高程偏差由-22.1 mm 逐渐变化为-26.9 mm，7月2—30日偏差由-13.3 mm逐渐变化为-20.5 mm，8月31日—10月27日偏差由-10.7 mm逐渐变化为-14.2 mm，10月28日—12月2日偏差由-10 mm逐渐变化为-17.5 mm，说明施工期间轨面处于持续下沉状态；另外，分别经7月19日、8月30日、10月27日3次精调后，轨面高程变化明显，分别由-26.9 mm直接抬升为-13.3 mm，由-20.5 mm直接抬升为-10.7 mm，由-14.2 mm 直接抬升为-10 mm，说明精调对轨面高程影响显著。另外，9月12—13日出现了轨面高程突然抬升的情况，原因为施工单位在施作水平旋喷桩时，注浆压力未控制得当，引起轨道板结构被注浆压力顶起的情况，从而引起轨面高程变化。

2016年各断面轨面高程偏差随时间变化曲线见图2。可知，轨面高程偏差均为负值，说明各断面轨面高程均低于设计高程；里程K2247+524—K2247+528处于沉降漏斗的中心区域，7月4—19日各断面轨面高程处于持续下沉状态，越靠近漏斗中心，下沉量越大，7月19日轨面高程偏差最大点K2247+526为-26.9 mm，最小点K2247+546为-10.8 mm，相差16.1 mm；经7月19日精调后，7月20日各断面轨面高程最大偏差-13.3 mm，最小偏差-7.2 mm，相差6.1 mm；通过精调，不仅使各断面轨面高程偏差变小，同样也使得轨面高程曲线变得平缓。再对比8月3日，8月31日及10月27日,10月28日轨面高程曲线，精调同样也达到了相应的效果。

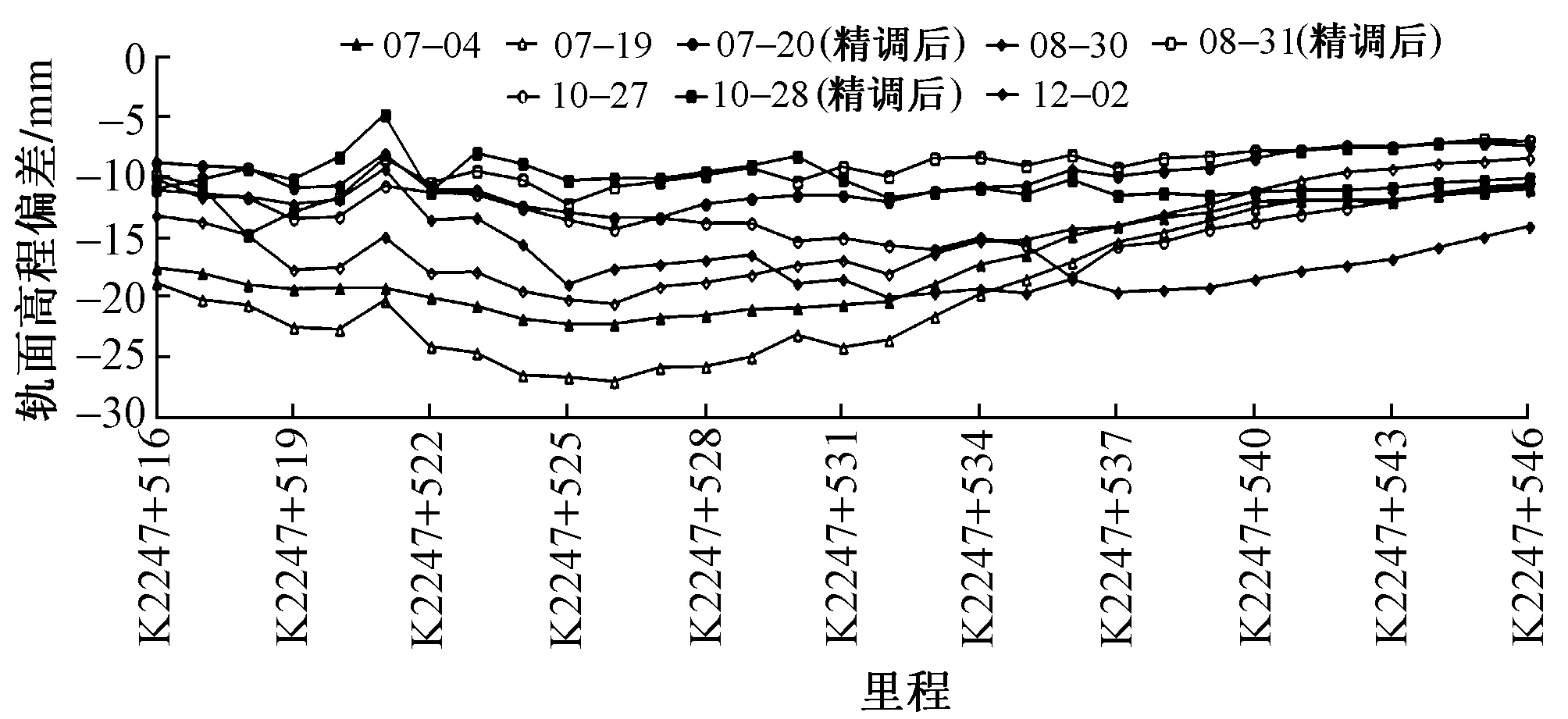
图2 各断面轨面高程偏差随时间变化曲线(2016年)

3.3.2 轨道平面位置

2016年K2247+526断面轨道平面位置偏差随时间变化曲线见图3。可知：7月4日—10月27日中间虽然经历7月19日,8月30日2次精调，轨道平面位置偏差变化基本不大，介于-4～-7 mm，曲线平缓且较稳定，说明这2次精调未对轨道平面位置进行调整。10月27日对轨道平面位置进行了精调，使得轨道平面位置偏差从10月27日的-5.7 mm 调整到10月28日的-1.5 mm，说明精调效果显著。

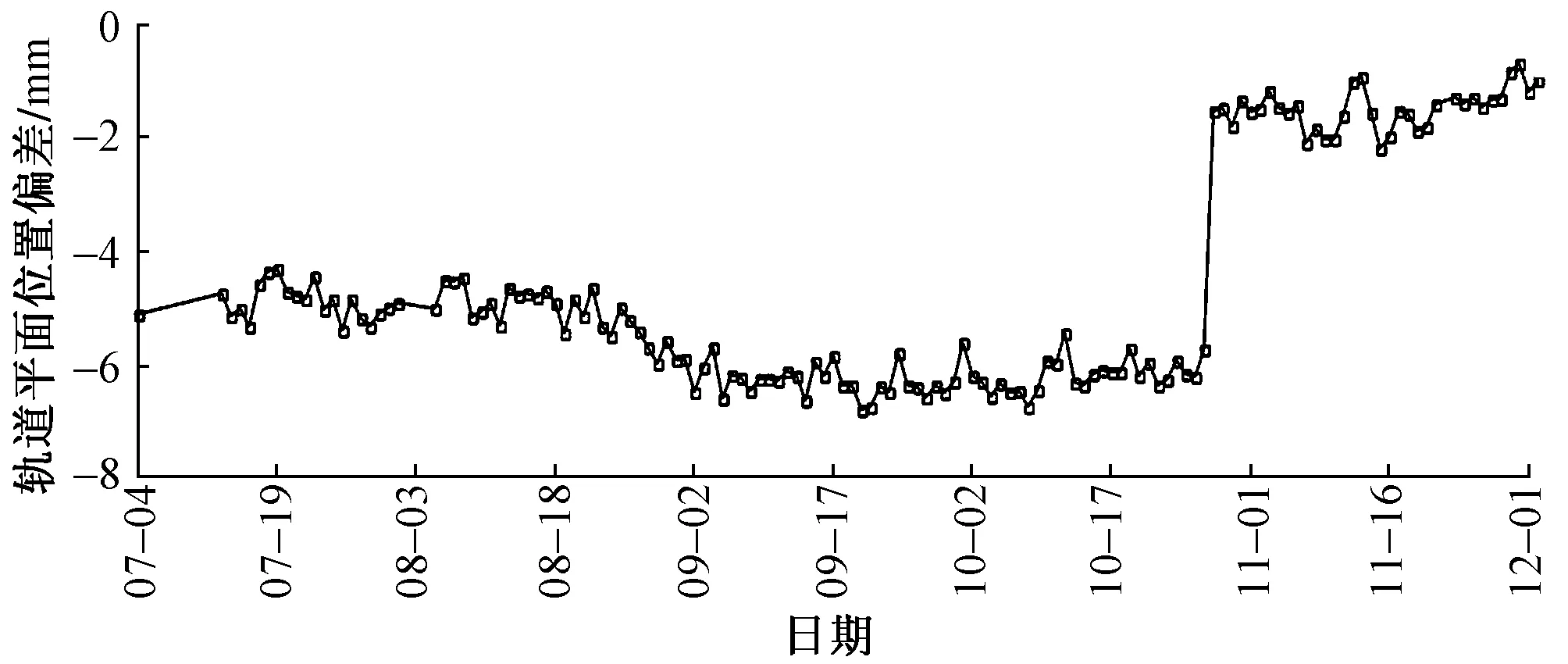
图3 K2247+526断面轨道平面位置偏差随时间变化曲线(2016年)

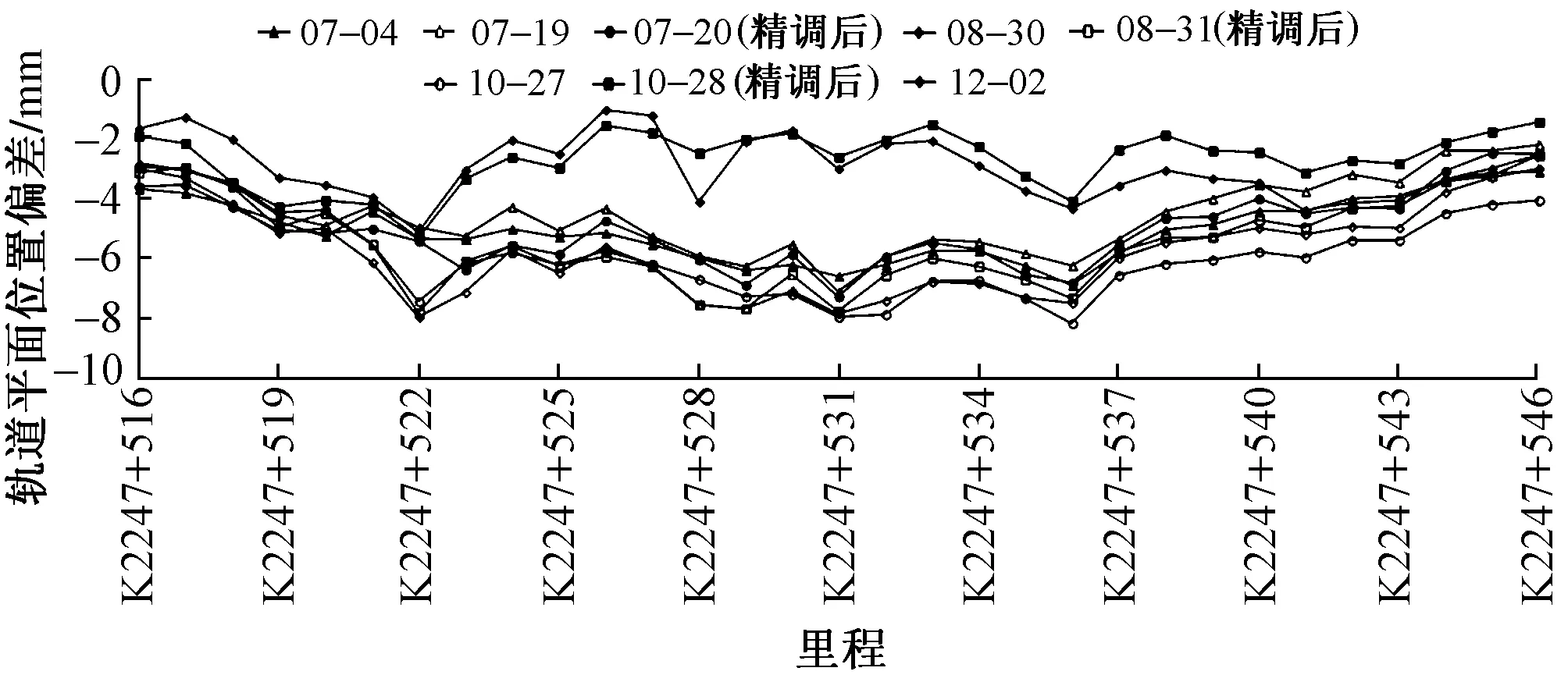
图4 各断面轨道平面位置偏差随时间变化曲线(2016年)

2016年各断面轨道平面位置偏差随时间变化曲线见图4。可知：轨道平面位置偏差均为负值，说明各断面轨道平面位置均位于设计位置左侧；7月4日—10月27日各断面轨道平面位置曲线基本处于重叠状态，说明这段时期轨道平面位置变化不大，同样也说明7月19日,8月30日2次精调未调整轨道平面位置；10月28日曲线明显与7月4日—10月27日之间的曲线分离，向0靠近，说明10月27日对轨道平面位置进行了精调，精调后轨道平面位置偏差明显减小，精调效果显著。

3.3.3 水平(超高)

2016年K2247+526断面水平偏差随时间变化曲线见图5。可知：K2247+526断面水平偏差基本上为负值，说明其断面基本处于左轨低于右轨状态；K2247+526断面水平偏差均在允许偏差范围内。7月4日—10月27日中间虽然经历7月19日,8月30日2次精调，水平偏差变化基本不大，介于-1～-4 mm，曲线平缓且较稳定，说明这2次精调未对轨道水平参数进行调整。10月27日对轨道水平参数进行了精调，使得轨道水平偏差从10月26日的-2.9 mm调整到10月29日的-0.4 mm，说明精调效果显著。

图5 K2247+526断面水平偏差随时间变化曲线(2016年)

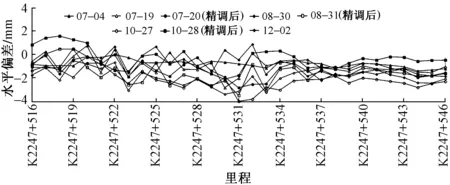
图6 各断面水平偏差随时间变化曲线(2016年)

2016年各断面水平偏差随时间变化曲线见图6。可知：大多时间各断面水平偏差为负，随着时间推移部分断面水平偏差存在由负变正的情况，说明大部分时间左轨低于右轨，左右轨存在不均匀沉降的问题并且随着轨道板的沉降量增大在缓慢变大。7月4日—10月27日各断面水平偏差曲线基本处于重叠状态，说明这段时期轨道水平变化不大，各断面水平偏差均在允许偏差范围内。10月28日水平偏差曲线明显与10月27日曲线分离，向0靠近，说明精调后轨道水平偏差明显减小，精调效果显著。

3.3.4 轨距

2016年K2247+526断面轨距偏差随时间变化曲线见图7。可知：K2247+526断面轨距偏差大多不在允许偏差范围内，超过了预警值。7月4日—10月27日中间虽然经历7月19日,8月30日2次抬道，轨距变化基本不大，处于-2 mm上下，曲线平缓且较稳定，说明这2次精调未对轨距进行调整。10月27日对轨距进行了精调，使得轨距偏差从10月26日的-2.0 mm 调整到10月29日的-3.3 mm，说明精调后轨距进一步收窄。

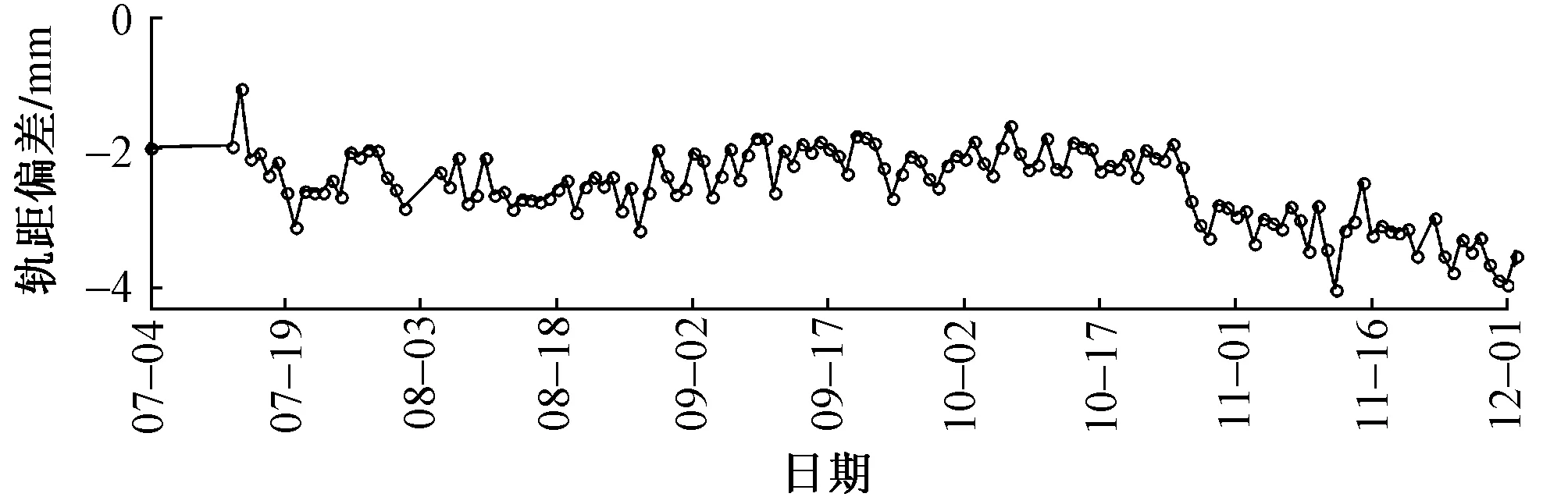
图7 K2247+526断面轨距偏差随时间变化曲线(2016年)

图8 各断面轨距偏差随时间变化曲线(2016年)

2016年各断面轨距偏差随时间变化曲线见图8。可知：各断面轨距偏差均为负值，说明各断面轨距均小于标准轨距；部分断面轨距偏差在某一时间段内超出了允许偏差范围。7月4日—12月2日各断面轨距偏差曲线基本在-2 mm上下波动，但波动幅度不大，说明轨距偏差一直较为稳定。

在监测过程中发现无砟轨道部分几何状态参数已经达到二级超限的标准，广州南高速铁路工务段分别于2016年7月19日,8月30日,10月27日对施工路段的无砟轨道结构进行了精调。通过运用轨道几何状态自动监测系统对施工区域不间断地监测，保证了京广高速铁路的安全运营和施工安全，下穿盾构隧道已于2016年12月17日成功穿越京广高速铁路。

4 结论

1)在一定的技术条件下，机器人测得的轨道几何状态参数轨面高程、轨道平面位置、水平、轨距中误差皆在1 mm以内，理论上可以满足轨道几何状态参数的测量精度要求。

2)实测数据表明机器人与安博格小车测得的轨道几何状态参数相关性高，差值离散性很小，机器人测得的轨道几何状态参数是可靠的，用机器人代替安博格小车在固定区段进行轨道几何状态的自动监测是可行的。

3)现场的实际应用中能准确地在线实时监测施工区段轨道几何状态的变化情况，保证高速铁路的运营安全，值得在实践中推广。

轨道几何状态监测系统天窗时间内测量值较为可靠稳定，但在运营时段如何排除列车对测量造成的影响是后续的研究方向。