交直流微电网三阶段分布式状态估计方法

赵小波, 严正, 徐潇源

(上海交通大学 电子信息与电气工程学院，上海 200240)

0 引 言

大规模分布式电源接入配网，使配网呈现新的形态，微电网有助于提高分布式电源消纳能力，增强配网可靠性[1]。交直流微电网由交/直流微电网以及变换器组成，可减少换流装置，降低损耗，逐渐引起研究者重视[2]。针对其运行控制已有许多研究[3]，但状态估计方面的研究还较少。文献[4]研究了交直流微电网集中状态估计，有一定的创新意义。

然而，相比于集中式方法，分布式方法在计算效率、通信和隐私保护等方面具有优势。集中状态估计器需收集系统所有信息统一计算，计算效率低，通信量大，当子系统内的信息未能更新时，将导致状态估计过程中断。而在分布式方法中，各子系统均有状态估计器，通过并行求解，最终可以得出状态量。文献[5]1研究了交直流微电网的分布式状态估计方法，但该方法只适用于量测方程呈线性的情况。因此本文在此基础上，基于三阶段状态估计理论[6]建立了集中式状态估计模型，并基于拉格朗日松弛法[7]实现了交直流状态估计的解耦，提出了三阶段分布式状态估计方法。算例仿真验证了该方法具有较高的精度与较好的收敛特性。

1 交直流微电网三阶段状态估计模型

文献[5]2中的交直流微电网状态估计模型为：

minJDC(xDC)+JAC(xAC)
s.tPAC+ηPDC=0

(1)

式中：xAC、xDC为交/直流微电网的状态变量;JAC、JDC为状态估计目标函数;PDC、PAC为由直(交)流侧流向交(直)流侧的有功;η为传输系数。一般而言，量测量与状态变量是非线性的，模型(1)非凸，分布式算法不适用。本文采用三阶段(第一阶段状态估计，中间变量非线性转换阶段以及第三阶段状态估计)状态估计理论，量测量与状态变量保持线性关系。

在第一阶段，定义以下变量：

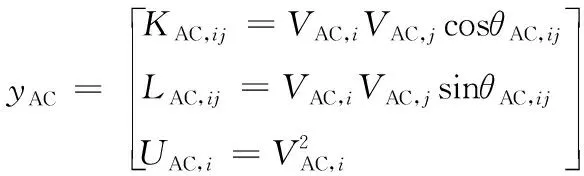
(2)

式中:yAC、yDC为交/直流微电网的状态变量;VAC,i、θAC,i为交流节点i的电压幅值和相角;VDC,i为直流节点i的电压值。交直流微电网量测均可由yAC与yDC线性表示，则状态估计模型有以下形式：

minJDC,1(yDC)+JAC,1(yAC)
s.tEACyAC-CA+η(EDCyDC-CD)=0

(3)

JAC,1(yAC)=(zAC-hAC(yAC))TWAC,z(zAC-hAC(yAC))
JDC,1(yDC)=(zDC-hDC(yDC))TWDC,z(zDC-hDC(yDC))

(4)

式中:zAC、zDC为交直流微电网中的量测量;hAC(yAC)、hDC(yDC)为量测方程;WAC,z、WDC,z为量测误差权重系数矩阵;EAC、EDC、CA与CD均为已知值。模型(3)为凸优化问题，等式约束使得交直流之间存在耦合，交直流状态估计无法直接解耦，第2节中将对分布式过程阐述。

第二阶段为中间变量非线性转换。对于交直流微电网，中间变量uAC以及uDC有以下非线性转换过程：

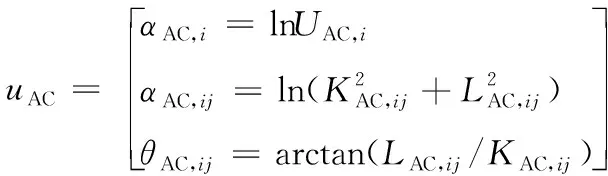
(5)

第三阶段将第二阶段的中间变量uAC以及uDC作为等效量测量，交流微电网的状态变量为xAC=[lnVAC,i;θAC,i]，直流微电网的状态变量为xDC=[lnVDC,i]。uAC及uDC可由xAC与xDC线性表示，第三阶段的交直流微电网状态估计模型如下：

min(uAC-AACxAC)TWAC,2(uAC-AACxAC)+
(uDC-ADCyDC)TWDC,2(zDC-ADCxDC)

(6)

式中:AAC、ADC为常系数矩阵;WAC,2、WDC,2为误差权重系数矩阵，求解可由交直流并行计算。

2 交直流微电网分布式状态估计方法

在三阶段模型中，第二、三阶段均可由交直流并行求解，而第一阶段中，等式约束使交直流存在耦合。拉格朗日松弛法是一种分散优化算法，其思想是将造成问题难以分布式求解的难约束松弛到目标中，从而原问题可分成多个子问题并行求解。采用拉格朗日松弛法对式(3)求解，迭代过程如下：

(7)

(8)

(9)

式中:λ为拉格朗日乘子;k为迭代数。迭代收敛的条件设为|λk-λk-1|/|λk|≤ε。λ协调交直流侧以使等式约束得到满足。图1为基于拉格朗日松弛法的第一阶段分布式状态估计实现机制示意图。式(7)与式(8)的求解分别由交/直流微电网状态估计器根据本地信息并行计算，最终满足收敛条件即结束迭代。

图1 第一阶段分布式机制

本文所提出的分布式方法分为三个阶段，均由交/直流微电网并行计算，在第一阶段需要交直流微电网之间进行信息传递。图2为本文所提出的三阶段分布式状态估计方法的流程。

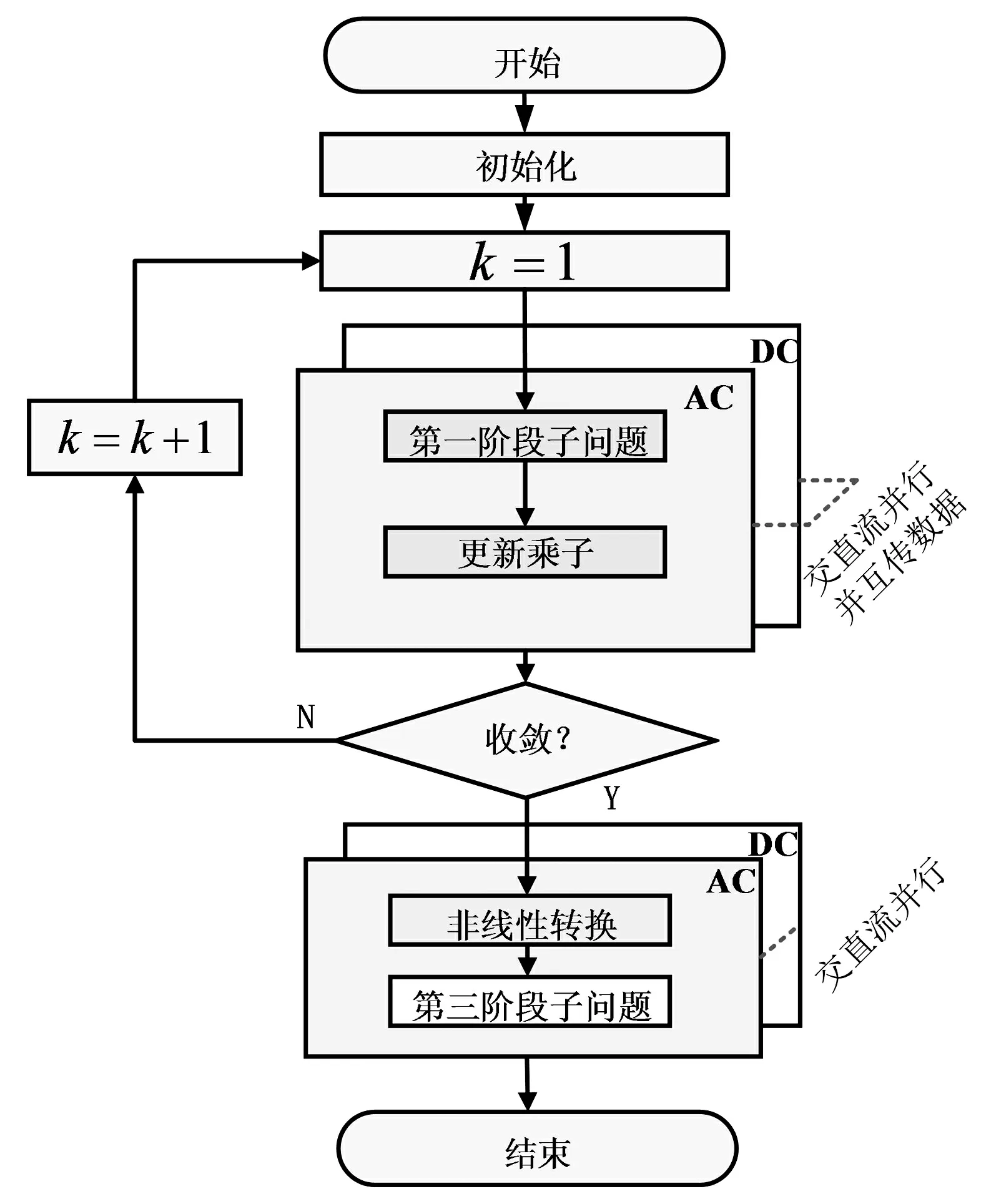
图2 三阶段分布式状态估计流程

3 仿真分析

本文采用文献[5]4中的仿真系统。在潮流计算基础上叠加随机正态分布误差得量测值,包括：交/直流节点1～5的电压幅值(标准差为0.2%),注入功率(标准差为2%)；交/直流节点1～2及节点1～3线路的电流幅值(标准差0.3%)。非特殊说明情况下，ρ取为20，ε=0.000 1。仿真结果在配有Intel双核2.4 GHz CPU和2G内存的台式机上获得。

为验证本文方法的精确性，对直接求解式(1)与采用本文方法的结果进行对比。由表1可知，采用本文方法与最优结果存在一定的误差，但误差极小，在实际应用中可以忽略不计。

表1 状态估计结果精度比较

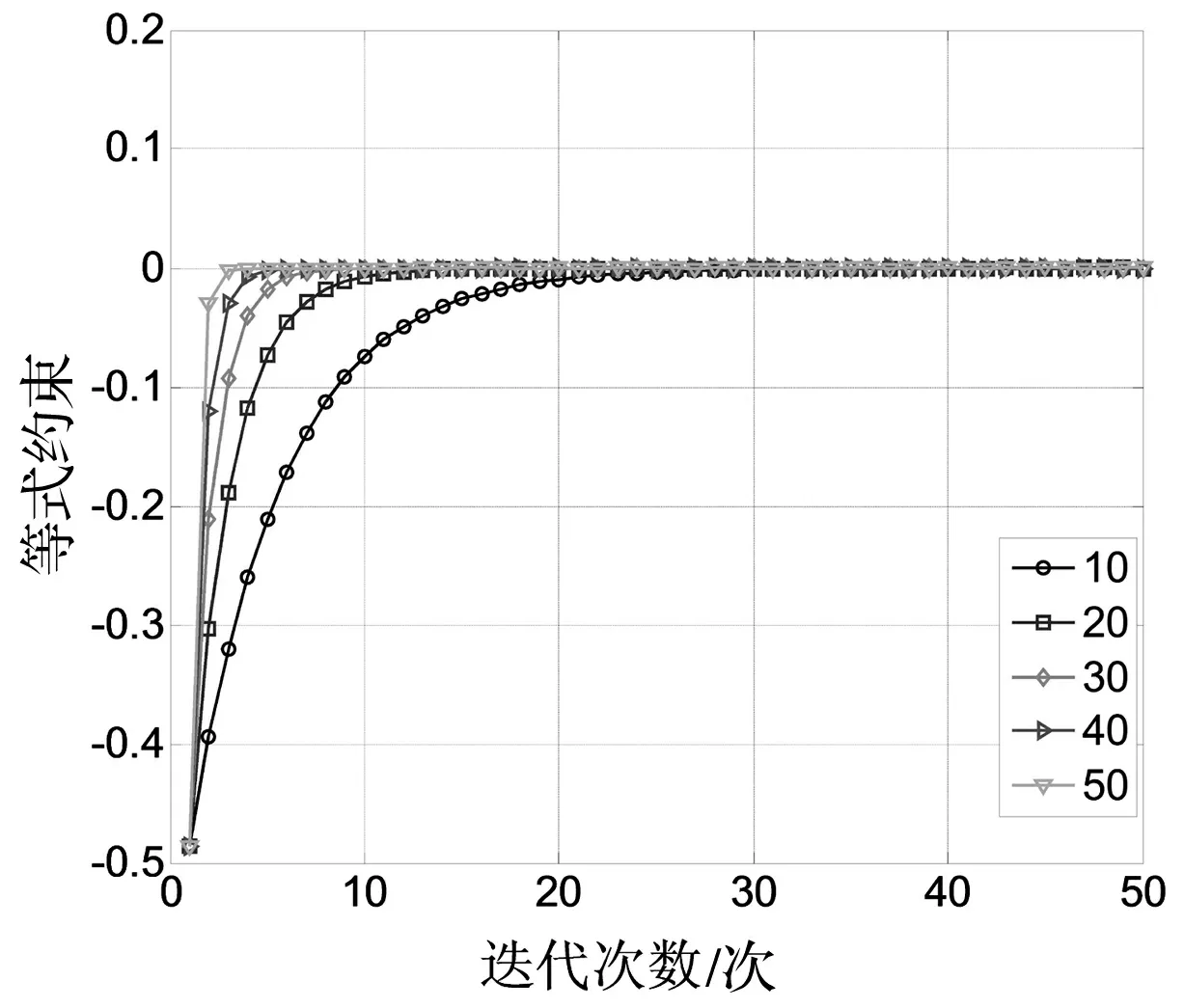
图3 第一阶段等式约束迭代

下面着重对第一线性阶段的分布式状态估计算法进行仿真分析。图3为ρ取不同值时，等式约束的迭代过程。由图3可知，通过迭代求解，最终PAC+ηPDC趋于0，等式约束可以满足。

交替方向乘子法[8]也是一种常用的分布式方法，将本文方法与基于交替方向乘子法的分布式方法进行对比。表2～表3给出了收敛性以及运算时间的对比。由表2可知，拉格朗日松弛法的收敛性优于交替方向乘子法。另外，交替方向乘子法在目标函数中增加二次惩罚项，单次计算时间比拉格朗日松弛法长。收敛次数与单次时间两方面的因素导致拉格朗日松弛法的计算时间小于交替方向乘子法。表3验证了这一点。综上所述，基于拉格朗日松弛法的分布式状态估计方法优于基于交替方向乘子法的分布式状态估计方法。

表2 分布式方法收敛性对比

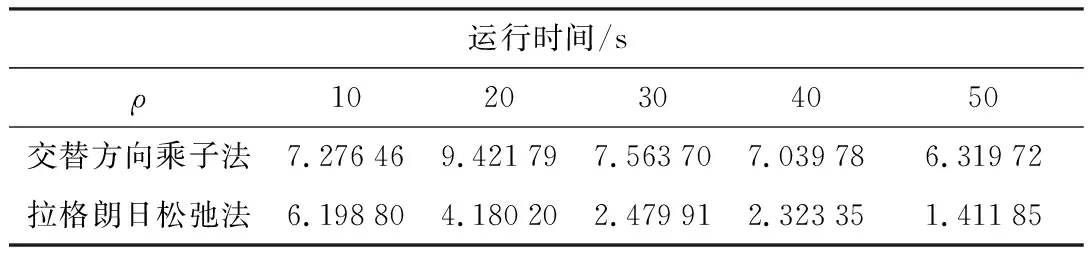
表3 分布式状态估计运行时间对比

4 结束语

本文针对交直流微电网提出了一种三阶段分布式状态估计方法。第一阶段与第三阶段为状态估计环节，第二阶段为非线性转换环节，三个阶段均由交直流微电网分布式计算。本文所提出的分布式状态估计方法不需要集中协调机制，仅在相邻的交直流微电网之间传递信息，通信量大大降低。最终的仿真算例表明该方法收敛性好，结果精度高。