永磁同步电机的自抗扰控制方法研究

张旭秀， 陆梦羽

(大连交通大学, 辽宁 大连 116028)

0 引 言

新世纪以来，在新型永磁同步电机( Permanent Magnet Synchronous Motor, PMSM)飞速发展的今天，非线性控制理论也在进行突飞猛进的发展，以矢量控制为基础的情况下，与更加先进的策略如神经网络控制，模糊控制，分数阶控制，滑模控制等[1-4]结合的控制方法越来越受到欢迎。众多非线性控制策略中自抗扰控制不依赖被控对象的数学模型，不仅可以自动检测被控对象的扰动，还可以对其扰动进行补偿，对因为参数变化或者有负载扰动变化的系统进行较好的控制，其强大的适应性和鲁棒性是很多控制方法难以达到的。然而由于经典自抗扰控制需要整定的参数的个数多，最普通的二阶系统需要整定个数就有十几个，针对调节复杂这一问题，越来越多的研究人员着眼于自抗扰参数设计的研究，提出一种不需要参数整定的自抗扰控制方式[5]，但是此类控制方法在应用于永磁同步电机(PMSM)时，受转动惯量(J)、负载突变(TL)等系统影响时，抗扰动能力会变差，超调量不仅增大，并且很难达到高稳态的控制要求。

因此，本文在非线性自抗扰的理论基础上结合前馈补偿控制，提出一种改进线性自抗扰方法，通过对非线性状态误差反馈(NLSEF)控制律的改进，保持了经典控制器的优点，减小了系统的误差，参数切换时平滑过渡，提高系统鲁棒性和抗负载扰动能力。本文所给方法的具体实施步骤：首先将前馈控制对比传统PID控制，在负载扰动发生变化时前馈控制能较好的观测并补偿扰动实现转速的更优控制;其次改进自抗扰对比前馈补偿，改进自抗扰的前馈补偿控制有响应速度快、超调量小、稳态误差小，改善了系统控制性能。

1 永磁同步电机的数学模型

永磁同步电机(PMSM)是一个强耦合、复杂的非线性系统，依照永磁体转子上方位的不一样，三相PMSM的转子结构有面贴式和内嵌式两种。本系统采用了面贴式PMSM为被控对象，考虑转动惯量小、结构单一、制造成本低的因素，Ld=Lq，假设转子上没有阻尼绕组，转速在基速以下时，给定定子电流，采用id=0的控制方式，更好地生成电磁转矩。PMSM 的数学模型在交直轴坐标系下为：

(1)

式中：ud、uq为定子电压在直、交轴上各自的分量;id、iq为定子电流在直、交轴上各自的分量;Ld、Lq为直、交轴的定子电感分量;ψd、ψq为直、交轴的定子磁链分量;R为定子电阻;ψf为转子上永磁体产生的磁链;J为转动惯量;P为磁极对数;TL为负载转矩;B为黏滞系数;与转速成正比。

2 自抗扰控制系统的负载转矩数学模型

2.1 前馈控制

与常见的闭环控制系统相比，前馈控制是一种开环控制系统，原理是测取进入过程的干扰包含外界干扰和设定值变化，并按其信号产生合适的控制作用去改变操作变量，使受控变量维持在设定值上。在控制系统中即保持被控对象输出不变的一种开环控制方法。一个典型控制模型可用图1表示。其中虚线框内为被控对象，系统包括控制通道和扰动通道。

GYD(s)：扰动通道传函

GFF(s)：前馈控制器传函

GYC(s)：控制通道传函

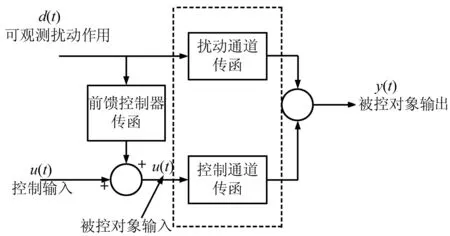
图1 前馈控制框图

被控对象与干扰信号无关，即传函G(s)=0，所以得出：

(2)

前馈控制的不变性原理包含动态不变性与稳态不变性[6]。动态不变性原理指的是在扰动d(t)作用下被控对象的输出y(t)在整个过度过程中保持不变，即Y(s)/D(s)=0，表示理想情况下调节过程中动态误差和稳态误差都为0。稳态不变性指的是在扰动d(t)作用下，被控对象的输出y(t)在整个过渡过程中动态误差不为0，而稳态误差为0[7]。

对患者PCI术前及术后1个月与3个月和1年的APTT（活化部分凝血活酶时间）、D-二聚体、Fib（纤维蛋白原）和INR（国际化标准比值）与PT（凝血酶原时间）以及TT（凝血酶时间）等六项凝血指标进行检测分析。同时对两组患者进行治疗后出现不良心血管事件（短暂性脑缺血发作、再发心梗、支架内血栓和缺血性脑卒中与再次置入药物洗脱支架治疗以及再次药物支架置入治疗等）以及出血事件（鼻粘膜出血、消化道出血以及皮下淤血与血尿等）进行记录。

2.2 直接计算负载转矩观测器

在PMSM数学模型中就可以计算负载转矩：

(3)

式中：TL为负载转矩;Te为电磁转矩;J为转动惯量;ωm为机械角速度;B为黏滞系数。本文这里给出了直接计算得到的负载转矩Simulink仿真图，如图2所示。

图2 直接计算的负载转矩观测器

此种观测器的跟踪负载转矩的能力很强，其实时性和跟踪效果统一。因此，由其构成的控制器应用于PMSM的控制系统中，给定转矩为5 N·m，在0.4 s时突加负载转矩为10 N·m，观测PMSM的转速输出，此种控制器的控制结果与传统的PID控制相比实时性会更好，对比图如图3所示。

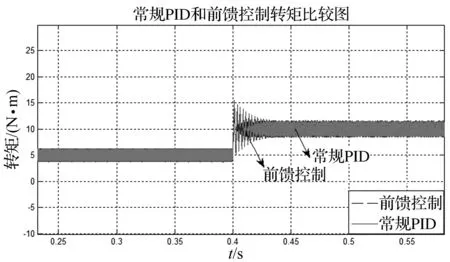
图3 前馈控制器与传统的PID控制转矩对比图

2.3 自抗扰控制器的线性化

自抗扰控制技术(ADRC)[8]是韩京清教授针对传统的PID控制的缺点与不足进行了改进提出的，它的设计不受被控对象的准确模型的影响，在鲁棒性和稳定性方面都比PID有显著提高。

非线性的自抗扰控制技术的三部分中都用到了非线性函数，对二阶系统而言其需要整定的参数多达十几个，文章的非线性状态误差反馈采用PI控制，以PSMS速度环一阶自抗扰控制为例，介绍线性化模型。ADRC数学模型包括：跟踪微分器(TD)，扩张状态观测器(ESO)，状态误差反馈控制律(NLSEF)。

跟踪微分器：

(4)

扩张状态观测器：

(5)

(6)

3 基于ADRC的PMSM负载转矩补偿控制系统的实现

3.1 负载转矩前馈补偿控制器的实现

前馈控制原理已阐述，需要用到控制通道及扰动通道，上面PMSM运动方程可以整理为如下式所示[9]：

(7)

当id=0时方程又可整理为:

(8)

(9)

3.2 控制系统仿真模型

将直接计算负载转矩观测器和前馈补偿器结合构成负载转矩补偿通道，输出直接补偿到交轴电流，PMSM的速度环线性化ADRC通过对转速误差的反馈补偿，输出q轴电流的参考值，与前馈控制器的补偿作用一起构成q轴电流环参考输入。系统模型如图4所示，dq轴电流环、逆变器、PMSM整体看作一个前馈-反馈控制系统的被控对象，其中反馈控制器采用线性ADRC控制器。

图4 基于ADRC的PMSM负载转矩观测控制系统模型

4 仿真及结果分析

为验证线性ADRC的PMSM负载转矩补偿系统的性能，本文利用Simulink对整个系统实现了仿真，电机各个参数如下：额定转速500 rad/s，定子电阻2.875 8 Ω，交轴、直轴分别为Lq=Ld=8.5 mH,转动惯量J=0.008 5 kg·cm2,极对数p=4,额定转矩为5 N·m,转子磁通φf=0.175 Wb。

图5是系统启动阶段的转速对比图，设额定转速为500 rad/s，0.4 s时突加转速到1 000 rad/s，额定负载转矩下进行仿真，从动态指标和稳态指标看出，改进ADRC控制的PMSM的负载转矩补偿具有不错的控制效果，改进线性自抗扰震荡频率和幅值较小，有更好的速降和恢复时间，最主要的是由于ADRC中ESO对未知扰动进行准确观测并补偿，这是自抗扰控制技术最大的优点。图6是在速度一定的前提下在0.6 s时增加TL的对比图。如图6所示，改进自抗扰振荡次数减少，剧烈程度也变小，稳态波动区间要小于前馈控制。

5 结束语

本文将自抗扰和前馈控制器结合起来的方法运用到高性能PMSM系统上，设计出速度补偿控制器，提升整体的抗负载扰动能力，综合比较非线性自抗扰多参数的复杂性，改进的自抗扰补偿器，保证动态稳定同时增加了鲁棒性。仿真结果显示，改进自抗扰前馈补偿的永磁同步电机调速系统具有较好的动静态特性，减少系统可调参数，增加系统鲁棒性。

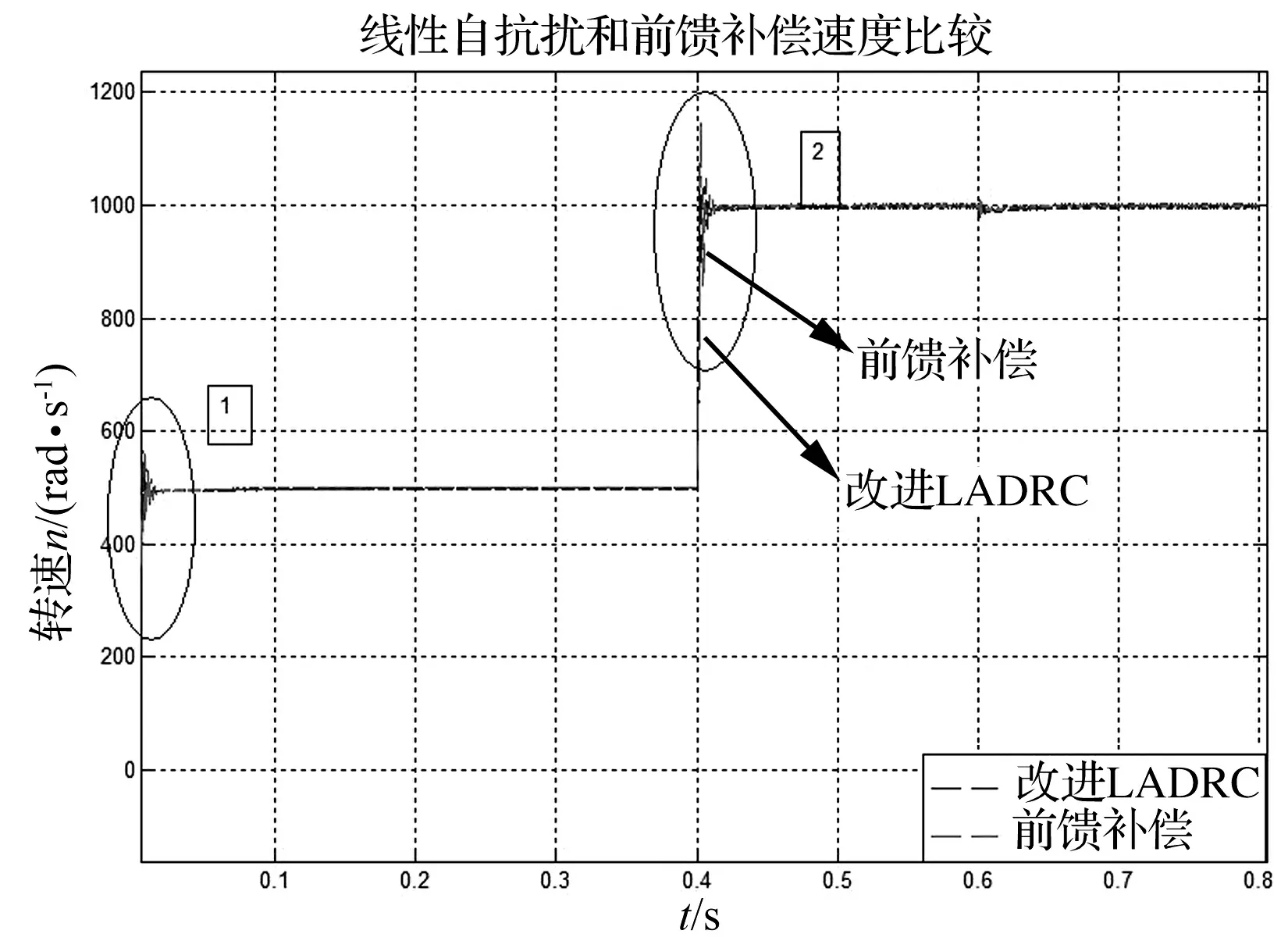
图5 速度动态响应曲线对比图

图6 转矩响应曲线对比图