基于模糊控制的模型车轨迹跟踪系统设计

沈芳, 韩国栋, 吴钫

(1.华中科技大学 自动化学院, 河北 武汉 430074； 2.中核兰州铀浓缩有限公司,甘肃 兰州 730065)

0 引 言

自动引导车辆是现代科技的产物，车载微机的性能日益强大[1]，并且能通过无线的方式接收控制中心的调度指令，完成启动、停止、路径规划、避障等功能，完美诠释了其智能化、无人化等特点。在移动方式上，以轮式移动最为常见[2]，应用范围不仅限于仓储业和制造业上，其他行业如：邮电、烟草、港口搬运等也都是自动引导小车的应用场所。其作为柔性运输的重要工具和自动化生产的典型代表，是我国高新技术研发的重点。在工业化生产制造中，性能卓越的模型车控制系统所担当的角色越来越受到国内外学者的高度关注。

此系统构建是以小车视觉[3]为基础，将模糊控制理论应用于小车控制研究。根据仿真波形及调试经验完善模糊规则表，快速消除运行过程中产生的偏差，实现轨迹的快速准确跟踪。

1 系统概要

1.1 控制系统组成

此系统主要由四个部分组成：摄像头、上位机、无线路由器、模型车，如图1所示。上位机给智能车下发不同的任务指令，并规划相应的执行路径；模型车接收到上位机指令后，自主解析数据，执行相应任务；摄像头按照一定的频率实时获取模型车位置，并发送给上位机和模型车，实现位置反馈；无线路由作为各个模块的网络连接，实现所有数据的传输。

图1 系统框图

图2 模型车运动模型

1.2 模型车数学模型

模型车采用三轮式结构，前轮为自由轮，后两轮独立驱动且通过差速来控制转向[4]，其曲线运动半径或转动方向可通过控制两轮速度差ΔV或旋转方向的不同来实现。小车运动模型如图2所示，以小车前进方向为x轴建立坐标系x0y，L是两独立驱动轮的轴距，0点是它们的中点，小车在行驶过程中受到外部干扰，产生前进方向上的角度偏差θ和距离偏差d，θ为小车当前行驶方向与规划轨迹方向的偏差，d为小车行驶过程两驱动轮中点与理想轨迹的偏移距离，R为智能车瞬时转向半径，VR、VL、Vo分别是右驱动轮、左驱动轮和车轮中点速度。

小车瞬时半径随着两驱动轮转速的改变而改变，瞬时半径R表达如式(1)所示。

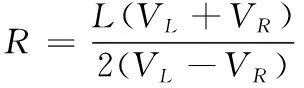
(1)

已知左右轮速度VL和VR，两驱动轮中点速度V0=(VL+VR)/2，中点速度在xy轴上的分量分别为Vx=V0cosθ，Vy=V0sinθ。若通过一段时间Δt，小车在行驶过程中出现了角度偏差Δθ和距离偏差Δd，RΔθ=V0Δt，Δd=VyΔt。当θ较小时Δθ≈tanθ，整理小车运动关系如式(2)所示。

(2)

这样就建立起了小车在t时刻及在t+Δt的运动关系。同时对上述两式左右时间求导，就是两偏差的变化率，整理如式(3)所示。

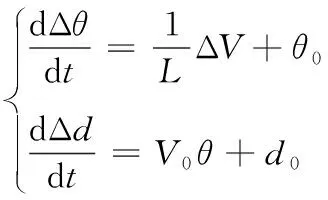
(3)

式(3)描述的是两偏差变量d，θ与左右驱动轮速度差ΔV之间的关系。θ0，d0分别表示小车初始位置的角度偏差与距离偏差。将模型车的运动偏差方程与驱动系统中电压与速度的传递函数结合起来，建立能描述整个被控对象的动态响应状态方程。驱动系统的数学模型通常是由输入输出的函数关系式建立的。此处选用系统辨识法[5]求得能够表示出系统本质属性的数学模型，如式(4)所示。

(4)

2 系统模糊控制

2.1 模糊变量的确定

本文设计一个双输入单输出模糊控制系统，系统偏差主要由d和θ组成，两者通过线性权重组合得到系统综合偏差，作为控制器第一个输入变量E，两偏差变化率的权重组合作为第二个输入变量EC，如式(5)所示。将调节两变量的电机输出电压差作为输出变量U。

(5)

根据试验测试，距离偏差d的基本论域为[-0.5,+0.5](单位：m)，角度偏差θ的论域为[-10,+10](单位：°)，计算两偏差量化因子为：Kd=6/0.5=12,Kθ=6/10=0.6, 距离偏差变化率dc论域为[-0.1,+0.1]，角度偏差变化率θc的论域为[-10,+10]，计算两偏差变化率量化因子为Kdc=6/0.1=60,Kθc=6/10=0.6。系统输出变量U的论域为[-0.6,+0.6](单位：V)，输出量的比例因子为：KU=0.6/6=0.1。两个输入变量的量化因子由式(5)计算为：

(6)

2.2 变量语言和隶属函数的确定

依据需求和控制的复杂程度，控制器的输入输出变量E、EC、U模糊集论域均取为：{-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6}，用字母表示为：NB、NM 、NS、ZO 、PS、PM 、PB。在跟踪理想轨迹时，一旦产生偏差，需控制系统能快速响应，所以输入输出变量的隶属函数采用三角型隶属函数。本文中，输出变量去模糊化方法采用重心法，即取隶属函数曲线与坐标轴围成的闭合区域的重心。经过多次试验及经验积累，总结出模糊规则表，如表1所示。

表1 模糊控制规则表

3 仿真及其结果

利用Simulink搭建仿真模型[6]如图3所示。设定初始角度偏差为1°(degree)，距离偏差为0.2 cm，设角度偏差权重为0.5，两驱动轮轴距L=16 cm。仿真模块设定相应初始值，运行结果如图4所示。

图3 控制器仿真模型

图4 d与θ的输出

如图4所示，偏角从初值1°(degree)开始减小，但是距偏差并不能马上减小，这是因为偏角还存在。此时距离偏差从0.2 cm到0.75 cm，等偏角减小到0进入负值域时，距离偏差开始减小。随着偏转角度的减小和控制规则的调整，偏转角度和距离偏差都趋于0，使得小车行驶在预定轨迹上。在20 s处，给小车一个0.4 cm的距离偏差，由仿真波形可以看出，系统能够快速响应，偏差最终收敛于零，达到跟踪理想路径的目的。

根据实际操作经验可知，角度偏差对路径跟踪较为敏感、直观，我们设角度偏差在综合偏差E的权重a分别为0.2，0.8，分析权重对系统性能的影响。

由图5、图6可知，角度偏差权重大于0.5时控制性能较好，多次仿真，当a=0.65时，系统响应迅速且超调较小。

4 试验研究

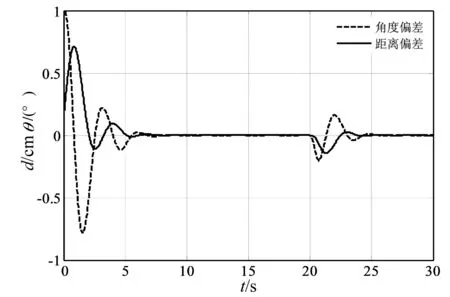
图5 a取0.2时，d与θ的输出

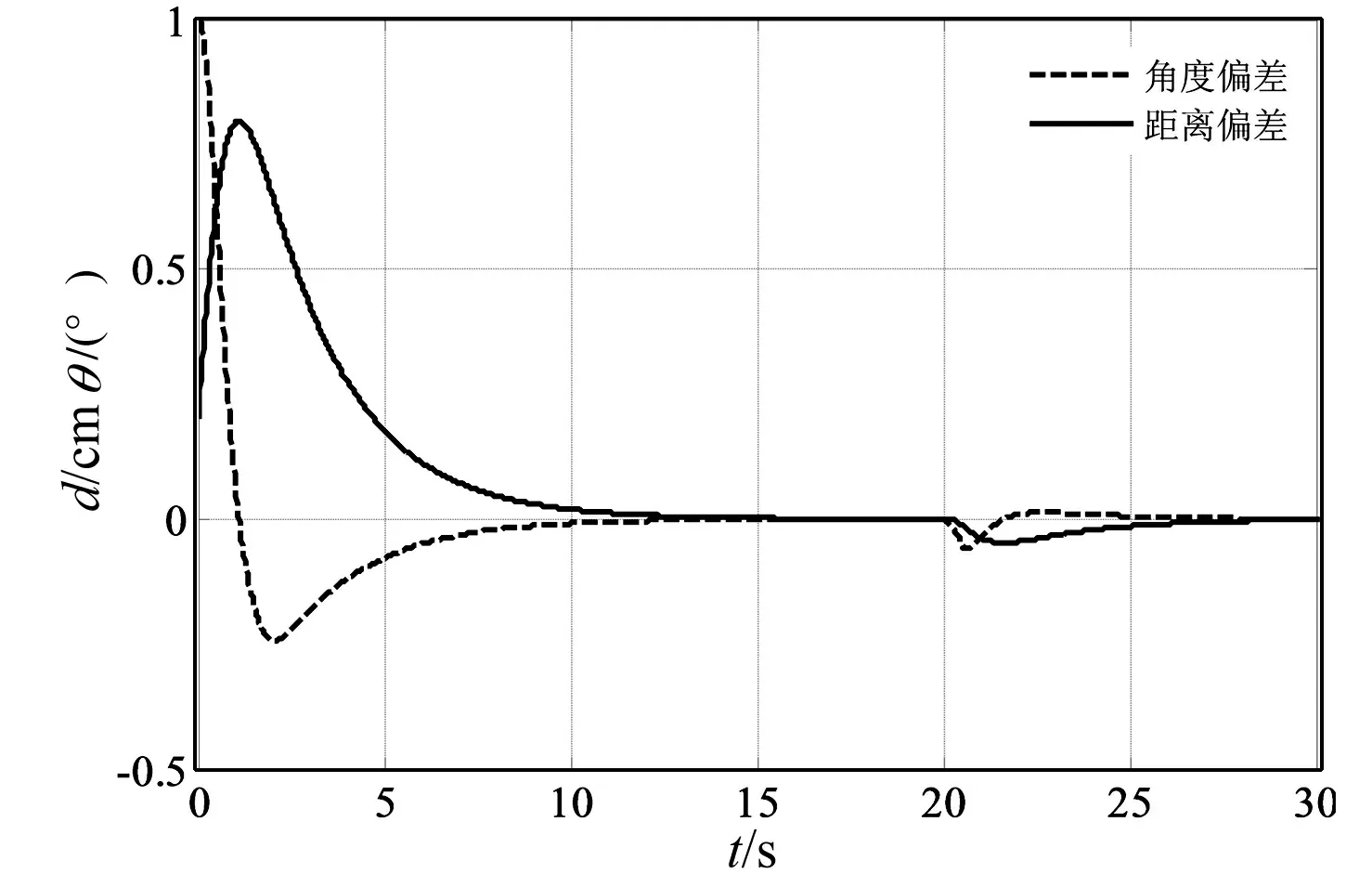
图6 a取0.8时，d与θ的输出

设计模型车控制电路，主要以低功耗嵌入式WIFI模块为核心，其内置高性能低功耗Cortex-M3微控制器[7]，另外还包括两个测量单元，测量单元分别测量电机的转速、电流和电压，为伺服电机控制算法提供状态反馈；一个双PWM发生单元，将控制单元得到的控制信号转化为实际的控制输出；一个通信单元，接收ARM控制主机过来的命令信号，并把伺服机构的状态反馈给ARM控制主机和一个电池管理单元，系统结构框图和模型车样机分别如图7、图8所示。

图7 模型车系统结构图 图8 模型车样机

图9 小车实验基地路径跟踪地图

图9所示为小车实验基地路径跟踪地图，上位机给小车规划一段轨迹，并根据摄像头反馈回来的小车坐标位置绘制出行走路径。开始运动时，在原点处小车偏离理想轨迹0.5 m，小车很快调整至规划路径。运行至圆弧阶段时，由于在圆弧处角度变化率较大，调整时间相对较长，但还是能稳定跟踪。在最后一段直线轨迹处，小车受到一个外部干扰，产生0.3 m的距离偏差和5°(degree)的角度偏差，由于角度偏差会优先调节，距离偏差会有所增加；经过一段时间两者偏差均减小至零，小车恢复到规划路径。

5 结束语

从试验结果可以看出，该轨迹跟踪控制系统能快速调整偏差，并回归至理想轨迹，验证了模糊控制系统的可行性与高效性，为以后的试验研究提供了理论依据和技术手段。