基于相对性原理的洛伦兹变换

刘志明，刘春清

(长春工程学院理学院，长春 130012)

0 前言

爱因斯坦分别于1905年6月30日和9月27日在德国《物理年鉴》(Annalen_der_Physik)上发表了“论运动物体的电动力学”[1]和“一个物体的惯性(质量)依赖于它的能量吗？”[2]两篇论文，系统地探讨了物质运动的时空—物质相关性问题，奠定了相对论物理学的坚实基础。在《论运动物体的电动力学》一文中，爱因斯坦提出了两条具有公理意义的假定：真空中光速不变性(下称“光速不变原理”)和物理规律的“形式”不变性(下称“相对性原理”)。

光速不变原理的理论支持来源于真空无源区麦克斯韦方程组的基本性质，依据该方程组得到的电磁波动力学方程中，传播速度是真空属性量，仅仅由真空介电常量和真空磁导率决定，不依赖于惯性系的选择，从而导致光速具有时空属性本质；导致爱因斯坦提出光速不变原理的实验推动因素则是迈克耳孙-莫雷在寻找绝对静止参考系(又称以太参考系)的负性结果[3]，这一结果促使爱因斯坦放弃“以太”基础上的电磁运动思想，直接讨论时间和空间的关联性，并且从光速不变原理出发得到了惯性系之间的洛伦兹变换，系统地阐述了洛伦兹变换的物理意义，由此打开了物质世界研究的另一扇大门。

对于时间和空间之间的关系而言，两者究竟是相互独立、各自均匀的，还是相互关联、相互影响的？直至爱因斯坦的深入思考之前，一直被想当然地忽略，而且在此思想基础上建立了伽利略变换，用以描述运动对惯性坐标系的依赖关系。但是，仅进行对称分析、因果分析，就会发现惯性系之间的伽利略变换的时空描述局限，下面采用如图1所示的惯性系模型为例加以说明。

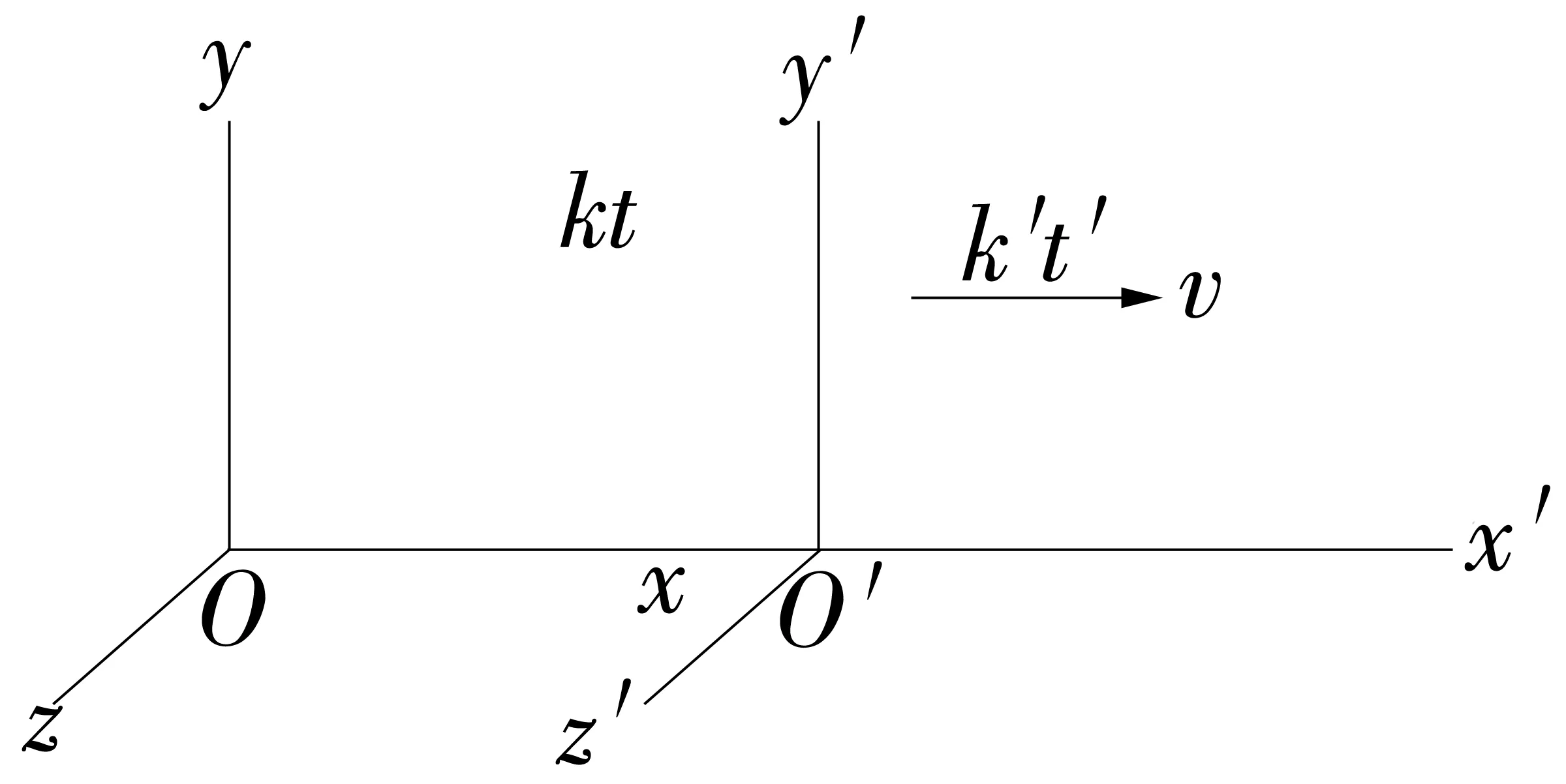
图1 相对匀速平动的两个惯性系

图中两直角坐标系x轴重合、y轴和z轴各自相互平行、分别固定于两个沿着x轴相对匀速运动(速率为v)的参考系上，并且假定坐标原点重合为初始时刻。描述同一质点的运动，在一个坐标系(k)中测得的位置坐标为(x，y，z)，在相对于k匀速v向x轴正向运动的另一坐标系(k′)测得的位置坐标(x′，y′，z′)，两组坐标之间关系的伽利略变换表达为

x′=x-vt，

y′=y，

z′=z，

t′=t。

(1)

从数学表达的因果律进行考察，式(1)的第1式(x坐标变换关系)的意思是说，时间坐标在影响或者干扰着空间坐标的变换，而第4式则表明任意直角坐标分量都无法干扰时间坐标。从作用之相互性不难发现，伽利略变换存在非对称性瑕疵，因为即使科学进步到21世纪的今天，仍然没有证据表明时间坐标和空间坐标究竟哪个更为优越！弥补该缺陷的方法只能是假定

x′=χx-ηt，

y′=y，

z′=z，

t′=λt+μx。

(2)

从而建立对等的时空坐标关系。当然χ,η,λ,μ都应是常量，以保证该变换是线性的。除此之外，x′=0，y′=0，z′=0为k′系的坐标原点，在k系中运动速度为v，因此必有

η/χ=v，

所以式(2)又可以简化为

x′=χ(x-vt)，

y′=y，

z′=z，

t′=λt+μx。

(3)

3个未知参量的确定可以通过多种途径实现，其中最为独特的当属爱因斯坦基于光速不变原理的同时性定义和讨论方法，直接给出两个参考系中时间、空间坐标的微分关系，废弃了洛伦兹采用的“本地时间(local time)”概念，得到了全新解释的洛伦兹变换。然而，爱因斯坦的时空属性讨论较为抽象而晦涩，时常引起一般学者的歧义理解，本文将从爱因斯坦的相对性原理出发，通过真空无源区麦克斯韦方程组形式的惯性参考系不变性，直接确定洛伦兹变换关系式，意在突出洛伦兹变换的实证特性，从而易于为广大受众所接受，并且证明相对性原理和真空中的光速不变原理是相容的。文末对洛伦兹变换导致的运动学描述现象进行了适当阐述。

1 力学定律的伽利略变换不变性

爱因斯坦的相对性原理是一条较为模糊的原理，深入理解相对性原理需要认识什么叫做坐标变换下的物理规律不变性，下面以牛顿的质点动力学定律加以说明。

根据经典力学的时空观，位于相对平动的两参考系当中，描述同一质点的运动(图2)，其位置矢量、速度矢量和加速度矢量满足下述关系：

(4)

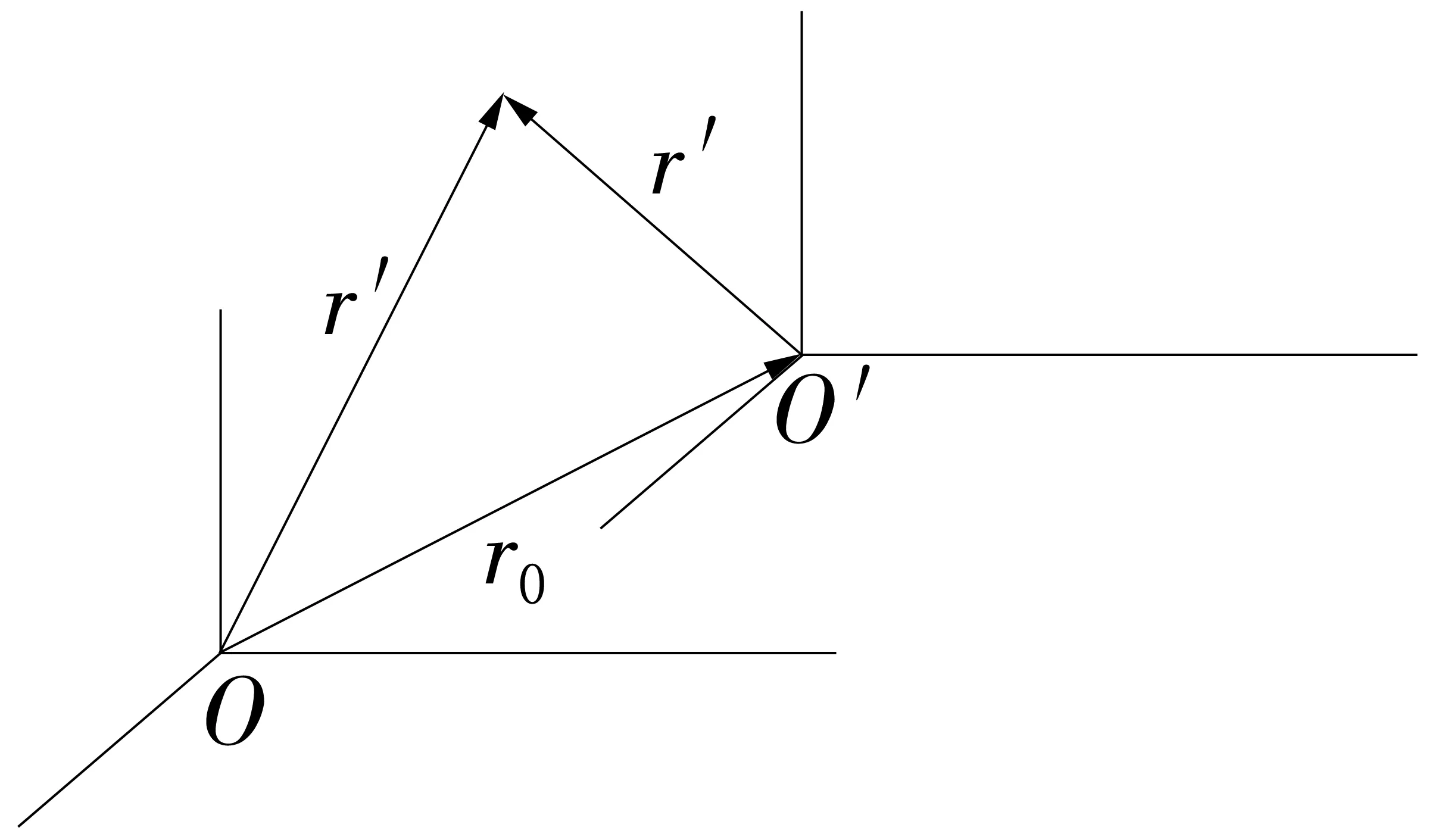
图2 牛顿—伽利略时空观下质点运动描述的参考系相关性

也就是说如果牛顿第二定律在两个参考系中都是成立的，那么必然的结果是

(5)

式(5)表明，在两个坐标系中同一质点所受的合外力是有差别的，这个差别来源于参考系之间的加速运动。然而，依据牛顿对力的定义，所谓力就是物体之间的相互作用，因此，一个质点的受力状况仅由它和其他物体之间的关系决定，不应与参考系的选择相关。所以，在不考虑质点与坐标系之间的相互作用的前提下，依据牛顿第二定律在两个坐标系中不能得到相同的运动描述结果(加速度)，这说明在加速参考系中牛顿第二定律不适用，严格来讲就是爱因斯坦提到的，在参考系、坐标系变换下物理定律的变与不变的问题。对于加速参考系相关的牛顿第二定律变换问题，成熟的处理方式是引进质点与坐标系相互作用的“惯性力”，以保证牛顿第二定律在两参考系中都能得到一致正确的结果[4]。

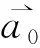
再来看看万有引力定律，假设在空间有两个质点，如果质量不因坐标系的运动而改变，则

显然

从而使得在两参考系中应用万有引力定律，得到相同的万有引力矢量，而且从形式上看来，加速参考系并没有(不能)改变其结果，加速变换和惯性系变换都不改变万有引力定律的因果关系。

再看质点的角动量定理：考察一个动量为mv的质点，相对于某定点r1的角动量

显然

(6)

这是说，加速参考系之间角动量定理不具有相同的形式，但是在惯性系之间角动量定理具有一致性的动力学因果。

以上几个例证分析表明，在非惯性系之间，动力学定律可能受到质点(物体)与参考系之间，相互作用的影响，形式发生改变，因果规律出现差异。然而，在伽利略变换下具有相同的形式，满足“相对性原理”。

2 麦克斯韦方程组的相对性

在国际单位制下，真空无源区的麦克斯韦方程组(微分形式)的矢量形式为[5]

(7)

如前所述，该方程中的ε0μ0是不依赖于惯性系的选择的。除此之外，两个旋度方程揭示了电磁之间相互作用和转化的因果(文献1中的麦克斯韦方程组没有考虑因果关系，因此形式上是逆因果的)。更为重要的是，空间某点的场量随时间的变化将决定另一个场量在空间的分布状况，显然暗示了时间坐标改变对空间的影响。因为处于封闭箱体中的观察者在不知道外边发生什么状况的前提下，箱内空间各点的电、磁场及其变化，除了认知为空间属性发生改变之外，没有可能推测出其他！仅从此点来看，伽利略变换极有可能破坏麦克斯韦方程组的因果律。

2.1 麦克斯韦方程组的伽利略变换困难

依据惯性系之间的伽利略变换，对于两个有旋方程，其分量式为

应用伽利略变换，进行整理，得到

(8)

如果在运动参考系中麦克斯韦方程组依然成立，必须具有如下形式

(9)

与式(8)比较，显然无法与运动参考系中的有旋性方程相符合，当然找不到那样的电场强度和磁感强度矢量，满足麦克斯韦理论确定的有旋因果。用爱因斯坦的话来说，应该是在惯性参考系之间的伽利略变换导致麦克斯韦方程组具有不同的形式或者表达方式，不具有一致的因果律。

2.2 基于麦克斯韦方程组不变性的洛伦兹变换推导

既然伽利略变换破坏了麦克斯韦方程组的因果关系，而麦克斯韦方程组本身是获得广泛实验支持的，问题应该出现在坐标变换上，应该是被忽略了的空间坐标对时间坐标的影响。现在假定惯性系之间的坐标变换采取式(2)，据此进行麦克斯韦方程组的惯性参考系变换，有

整理后

应用无源区的散度定理

立即得到

类似地将空间磁场的有旋性方程进行处理

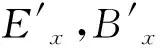
(10)

(11)

根据相对性原理，上述方程应当描述k′系中的涡旋场因果，场变换关系应当为

(12)

这说明k′坐标系中的电磁场是k系中场分量的线性叠加，考虑到场矢量叠加的唯一性，立即得到

(13)

求解该方程组即得坐标变换系数

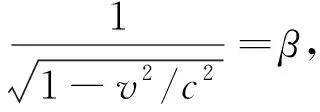
(14)

2.3 洛伦兹变换的几点说明

洛伦兹变换表明时空坐标具有相互关联性，所以，依据洛伦兹变换分析物理事件会得到与牛顿、伽利略时空不同的结论。

首先是同时性问题。假定在k参考系中有两个时间，一个发生在x1处，发生时刻为t1，另一事件发生于(x2，t2)，那么在相对于k以速度v沿着x轴正向运动的参考系k′中，两个事件的时空坐标分别为

两事件在k′中的时空间隔为

据此可以得到以下4个结论(假定相对运动速度非零)：

1)k系中同一位置发生的两个不同时事件，在k′系中仍然是不同时的，且事件先后次序不变，但是时间间隔发生变化，体现为间隔拉长(时间膨胀)。

2)k系中不同位置同时发生的事件，在k′系中观测结果一定是不同时的。

3)k系中不同位置同时发生的事件，在k′系中观察两者的距离一定是收缩的，或者等价地说，在k系中测量跟随k′运动的尺子，长度是收缩的，这称为尺缩效应。更为严格地说，本地测量本地静止长度是准确的原长，本地测量运动长度较之于跟随运动长度测得的长度较短。

尺缩问题一直是公众非难相对论的一个焦点，搞懂这个问题必须明确以下几点陈述：

①在任意惯性系中用相对于该惯性系静止的不形变尺子测量相对于该惯性系静止的不形变棒，其测量结果称为那只棒的原长。

定义该测量为本地测量，进行本地测量的惯性系称之为本地惯性系。相对于本地惯性系运动的惯性系定义为运动惯性系，在本地惯性系中用运动惯性系中的静止尺子测量运动惯性系中静止棒的长度称为异地测量。

②同样的不形变直棒，在不同惯性系中的本地测量结果相同，都为棒的原长。

③无法用本地不形变尺子测量运动惯性系中的静止不形变直棒的长度，也就是说，要想准确测定目标的长度，必须使尺子与目标进行比较，这本身就包含了尺子与目标对象相对静止的苛刻要求，但是两者“相对静止”后，由谁来进行比较，如何进行比较，那个进行比较的人是否运动则是另外一回事，也是相对论讨论的核心问题。

④在本地惯性系中可以使用运动惯性系中的不形变静止尺子测量运动惯性系中的不形变静止棒的长度，但是测得的结果要比本地测量结果小。

明确这几条之后就可以得到下述尺缩结论：

相对运动的两个惯性系A与B，如果相对运动速度v不为零，那么对于沿着v方向摆放、原长为l0的不形变直棒，拿到A中进行本地测量，长度为l0，拿到B中进行本地测量，长度同样为l0；拿到A中由B中的观察者进行异地测量，得到的长度是l0/β，拿到B中由A进行异地测量，结果仍为l0/β。

4)k系中不同位置、不同时发生的事件，在k′系中一般情况是不同时的，甚至有可能是次序颠倒的。

5)洛伦兹变换一旦确立，光速不变原理立即成立

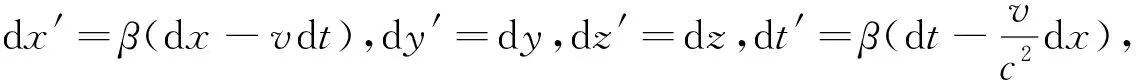
所以速度变换式为

对于在k系中沿着x轴正方向传播的电磁波，显然其速度矢量为vx=c，vy=0，vz=0，在k′系中有

对于在k系中沿着y轴正方向传播的电磁波，显然其速度矢量为vx=0，vy=c，vz=0，在k′系中有

而沿着任意方向传播的光波，在k系中

变换到k′系后，速度矢量为

应用速度变换关系

这是说光速在k′系和k系中的传播速度都是c，说明相对性原理和光速不变原理是相容的，甚至可以说是等价的。

这几条基本结论是洛伦兹变换对伽利略变换冲击性最大，也是最根本的结论。

在洛伦兹变换基础上的相对论运动学、动力学以及电动力学理论将经典物理理论的视野拓展到更为广阔的领域，取得了丰硕的成果。也正因此，每每提及爱因斯坦的相对论，洛伦兹变换的讨论是一个永远不可以绕过的重要论题。

3 结语

从以上推理可见，无论是从光速不变原理，还是从电磁场之麦克斯韦方程组的相对性出发，都能够得到一致性的重要结论：时间和空间不是相互独立的，两者存在相互影响，至少是相互关联的。相对于爱因斯坦在文献[1]中基于光速不变原理的时空讨论，以麦克斯韦方程组相对性为基础的洛伦兹变化推理虽然显得生硬，相对来讲更容易为大众所接受。自1905年相对论问世至今，质疑反对之声不绝于耳[6-8]。作者希望以此文为业界提供有益借鉴之外，更希望给对相对论持有异议者以启迪。