基于蒸发皿数据折算系数的绍兴地区蒸散量估算

季丹丹

(绍兴市柯桥区气象局，浙江 绍兴 312035)

参考作物蒸散量(ET0)是水资源规划与农业灌溉中一项非常重要的参考依据。世界范围内现有的ET0计算方法已达50多种，其中，世界粮农组织(FAO)推荐的Penman-Monteith公式由于理论依据充分、物理意义明确而得到了广泛应用。但是，Penman-Monteith公式中涉及的实测气象要素较多，包括气温、风速、相对湿度、日照时数、经纬度等，而目前常用的区域自动站没有办法提供上述完全的实测资料，使得ET0的实际计算存在现实困难，亟须寻求建立一个需要较少气象观测资料、简洁方便的方法计算蒸散量。

关于蒸发皿蒸发值(E0)与参考作物蒸散量之间的关系，国内外学者已开展深入研究，Jensen[1]、Doorenbos等[2]、Cuenca[3]、Snyder[4]已就估算折算系数(Kp)建立模型，用于实现E0与ET0之间的换算，并在全球不同气候区得到验证。由于国内的蒸发皿型号与国外有差别，因此Kp的使用受到限制。近年来，国内也有不少专家学者探寻适合当地的折算系数。周振民[5]以指标回归与定性资料确定了黄河下游引黄灌区的折算系数方程，虽然经验证精确度较高，但计算比较复杂。樊军等[6]利用2 m高处风速和平均相对湿度作变量，确定小型蒸发皿观测的蒸发量E0，估算黄土高原地区参考作物蒸散ET0的折算系数，虽然验证效果较好，但局地性较明显。

蒸发皿是目前大部分气象站广泛使用的气象观测仪器。E0是观测区域自由水面的最大可能蒸发量，是气温、风速、辐射等气象要素在综合作用下的直接表征。如果能找到蒸发皿蒸发值与蒸散量之间的相关性，就能更方便地计算出该地域的蒸散量，对指导农业生产和合理规划利用水资源均有很大助益。

绍兴位于浙江北部、杭州湾以南，呈现多种农副产品结合的农业产业结构，以平水水稻为主、山地杂粮为辅，农业产品比较丰富。本研究在已有的蒸散估算基础上，根据绍兴地区的实际气象观测资料进行本地化订正，以期得到适应于绍兴地区的折算系数。

1 材料与方法

1.1 材料

以绍兴站为研究对象，主要资料包括日平均气温、10 m高处风速、日照时数、相对湿度和小型蒸发皿蒸发等，时段为1981—2010年。区域地面为开放的草面环境，用来模拟自然状态。

1.2 基本原理及方法

1.2.1 Penman-Monteith公式

FAO推荐的Penman-Monteith公式：

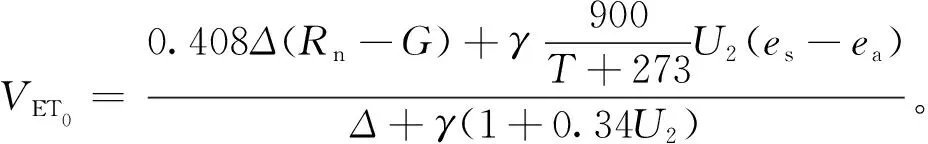
(1)

式中：VET0为参考作物蒸散量，mm·d-1；Δ为饱和水汽压温度曲线上的斜率，kPa·℃-1；Rn为净辐射，MJ·m-2·d-1；G为土壤热通量，MJ·m-2·d-1；T为2 m高度空气温度，℃；γ为湿度计常数，kPa·℃-1；es和ea分别为空气的饱和水汽压和实际水汽压，kPa；U2为2 m高处的风速，m·s-1。

我国普遍使用的小型蒸发皿为口径20 cm、高约10 cm的金属圆盆，安装后距离地面70 cm，提供了一种由辐射、风速、湿度、温度等水面蒸发综合影响的测定方法。如果小型蒸发皿蒸发值与蒸散量存在明显的线性关系，可以近似将二者的折算系数写成

(2)

通过上式即可计算出Kp值，然后以Kp为因变量，分析其与式VET0中各变量的线性关系。

1.2.2Kp的计算方法

研究发现，Kp主要与地面覆盖、风速和空气湿度有关。较为典型且常用的模型[7]为

(3)

式中：U10为10 m高处的风速，m·s-1；H为相对湿度，%；F为上风方向缓冲带的宽度，m。

在式(3)的基础上进行本地化修正：由于我国的蒸发皿安置与国外的方法不同，其距离地面的高度显著大于蒸发皿直径，因此F的影响较小，可以直接忽略[6]。另外，我国普遍采用10 m高风杆测风速，因此用U10替换式(1)中的U2。以Kp为因变量，U10和H为自变量进行多元回归并修订后，得到如下结果：

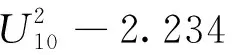
(4)

1.2.3 误差分析

为了评价模型的精度，将利用小型蒸发皿蒸发估算的蒸发皿蒸发值和利用Penman-Monteith公式计算的蒸散量进行对比，计算均方根误差(RMSE)。

2 结果与分析

2.1 蒸发皿蒸发与蒸散量之间的关系

基于Penman-Monteith公式计算出蒸散量，与蒸发皿蒸发值的年分布作对比(图1中a)，可以看出，1981—2010年间蒸发皿蒸发值与蒸散量都是递增的，蒸发皿蒸发值的增长速度为18.545 mm·a-1，蒸散量的增长速度为10.436 mm·a-1，虽然增长速率不同，但趋势都是浮动上升的。另外，无论是蒸发皿蒸发值还是蒸散量，在1982、1989、1995、1999、2001年等年份都出现一定程度的下降。这些结果说明，蒸发皿蒸发值和蒸散量在年尺度上增减幅度同步，但在速率上有所差异。

从蒸散量与蒸发皿蒸发值的月分布(图1中b)来看，两者的增减趋势相同：均在冬季量值最小，随着月份推移(1—12月)，先增长后减少，最大值都出现在7—8月，最小值出现在12月至次年1月，且6—7月间都有一次下降现象。总体来说，蒸发皿蒸发值和蒸散量在月尺度上增减趋势也相同。

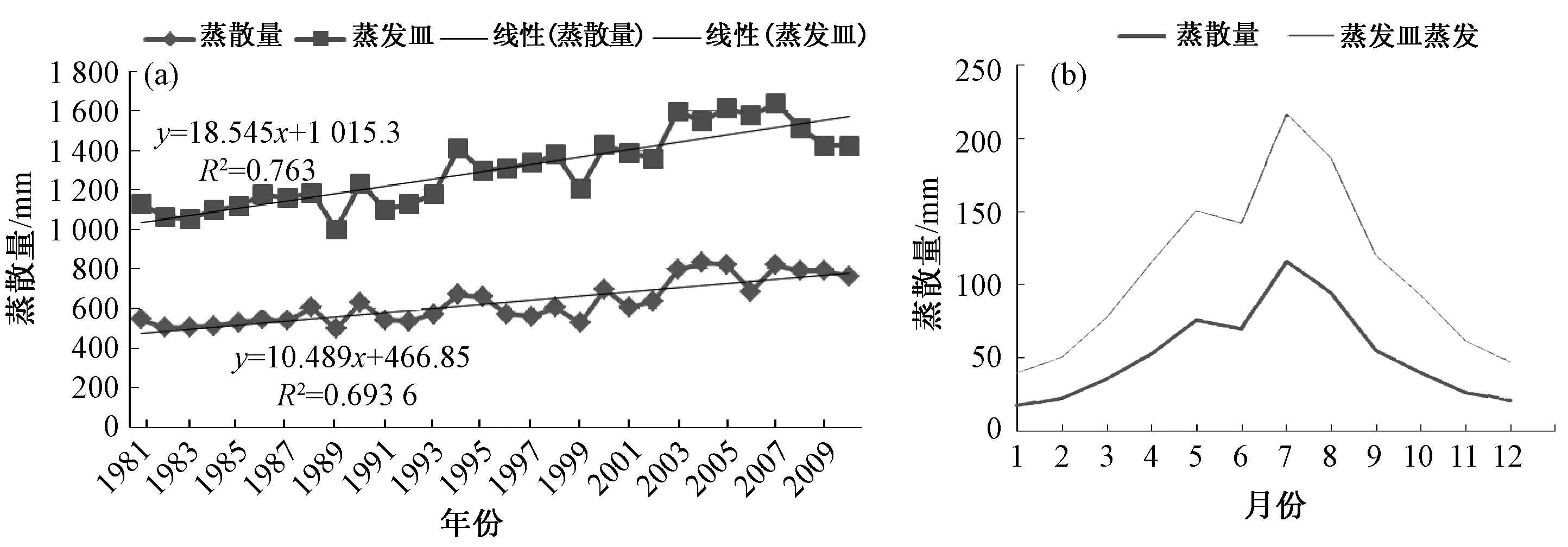
图1 蒸发皿蒸发值与蒸散量的年际变化(a)和月变化(b)

根据上述结果，将Penman-Monteith公式计算的日蒸散量和蒸发皿蒸发值进行线性回归分析，在日尺度上ET0和E0呈正相关关系(图2)，决定系数为0.831 3，相关性显著。

图2 蒸散量和小型蒸发皿蒸发值的关系

2.2 Kp的确定

将计算出的Kp值与E0相乘，就可以得到参考作物蒸散的估算值ETp，将其与经Penman-Monteith公式计算的蒸散值进行对比(图3)，决定系数为0.907 0，能通过显著性检验(P<0.05)，离散点基本都在1∶1范围内，说明估算效果较好。

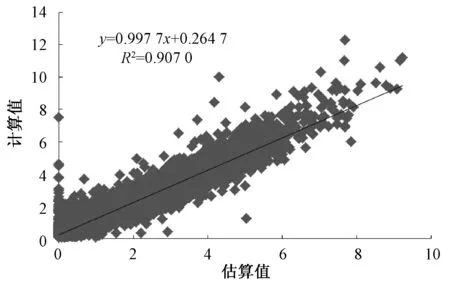
图3 估算参考作物蒸散量与Penman-Monteith公式计算的蒸散量的关系

2.3 误差验证

对计算结果进行检验，剔除明显错误的数值后，RMSE平均值为0.39，最大值为0.99，且能通过显著性检验(P<0.05)，在可接受范围内。分季节进行分析：春夏秋冬的平均误差分别为0.40、0.62、0.33、0.19，夏季的误差最大，其次是春季、秋季，最小的是冬季。利用SPSS 20.0对均方差与平均气温、相对湿度、平均风速和日照时数分别进行相关性检验，发现RMSE与平均气温、平均风速呈极显著正相关关系，与相对湿度呈极显著负相关关系，与日照时数呈显著正相关。说明平均气温、平均风速越高，误差越大。这与均方根误差的季节差异变化相符合。

3 小结

基于Penman-Monteith公式，利用绍兴站1981—2010年的气温、相对湿度、风速、日照时数及小型蒸发资料，研究适合于当地的基于小型蒸发皿数据估算参考作物蒸散的方法。结果发现，蒸发皿蒸发值与基于Penman-Monteith公式计算的蒸散量在年分布与月分布上趋势基本一致，且均呈正相关关系，因此可以用折算系数Kp来表示地表环境和开阔水面之间的差异。利用30 a的气象资料建立适用于绍兴的折算系数模型，并利用其估算出基于小型蒸发的蒸散量，与参考作物蒸散量进行对比分析，平均均方差误差为0.39，具有应用价值。在气象资料缺测或缺乏的情况下，根据10 m高处风速与相对湿度，即可确定折算系数，经计算可以得到蒸散量，对指导当地水资源利用和农业的可持续发展等具有积极意义。