基于冲击电压下电缆等效电阻值的绝缘状态评估新方法
李巍巍,甘德刚,朱轲,刘凤莲,何珉,周凯
(1. 国网四川电力科学研究院, 成都 610072; 2.四川大学 电气信息学院, 成都 610065)
0 引 言
交联聚乙烯(XLPE)电力电缆因其优异的电气性能而被广泛应用于城市输配电网络中[1-2]。相关研究表明,电力电缆的故障率与时间为一浴盆曲线,一般使用寿命约30年。而早期投入运行的电缆,随着时间的增加,有可能发生绝缘故障,导致可靠性下降。此外,电缆的安装并非十分规范,受实际规划的限制,电缆的共沟率往往较高,一旦发生绝缘故障,极易引发连锁反应,造成大面积的停电事故。所以,准确评估电缆的绝缘状态成为保证供电可靠性的关键。
国内外对电力电缆绝缘状态的评估进行了大量研究。包括直流叠加法[3]、交流叠加法[4]、低频叠加法[5]、tan δ法[6]、极化-去极化法[7-8]等。上述方法施加电压均不高,而某些缺陷在低电压下无法暴露,却极有可能在操作或雷电等过电压情况下突然发生绝缘事故。因此,如果能得到过电压下的电压和电流与电缆绝缘之间的关系,从而评估电缆绝缘的状态,可能会对缺陷的诊断更为准确。而国内在此方面的研究较为缺乏,大部分都是基于稳态电压下的绝缘状态评估,几乎没有基于过电压的绝缘状态评估研究。国外有利用冲击电压对电缆绝缘状态进行评估,主要利用传递函数和电介质光学介电谱[9],以及冲击电压下的频率响应[10-11]。提出了电力电缆的3元件等效电路模型[12]、4元件等效电路模型[13]和多元件串联的等效电路模型[14-17],用于时域反射法对水树进行定位,并未用于电力电缆绝缘状态的评估。
文章基于多元件串联模型,搭建了短电缆的多RC的串并联等效电路,理论分析了电力电缆的各层及整体等效电路参数的计算公式和推导方法,提出了一种基于冲击电压下电缆等效电阻值计算和绝缘状态评估的新方法,并通过理论推导和仿真计算进行了验证。
1 原理分析
1.1 电缆的等效电路模型
为了利用等效电路的参数值对电缆的绝缘状态进行评估,本文选取型号为YJLV22-8.7/15-3*95的XLPE电力电缆为研究对象,进行等效电路模型的建立。图1为剥除外护套和铠甲的单芯电力电缆的横截面图,其结构包括导体、内半导电层、XLPE层、外半导电层和铜屏蔽层。
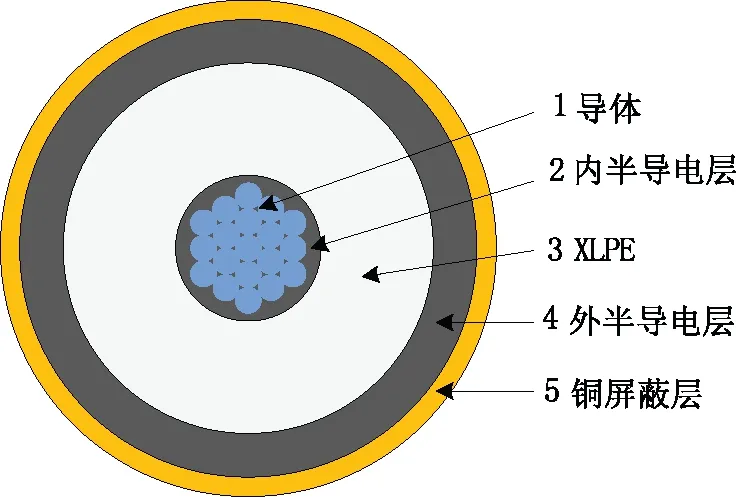
图1 XLPE电缆样本的横截面
由于水树缺陷的出现,会导致电力电缆绝缘的下降。基于此,建立了如图2所示的无水树电缆的等效电路模型,如图3所示的有水树电缆的等效电路模型。由于文中的研究对象是短电缆,所以在等效电路模型中忽略了短电缆的导体及铜屏蔽层的电阻和电感。
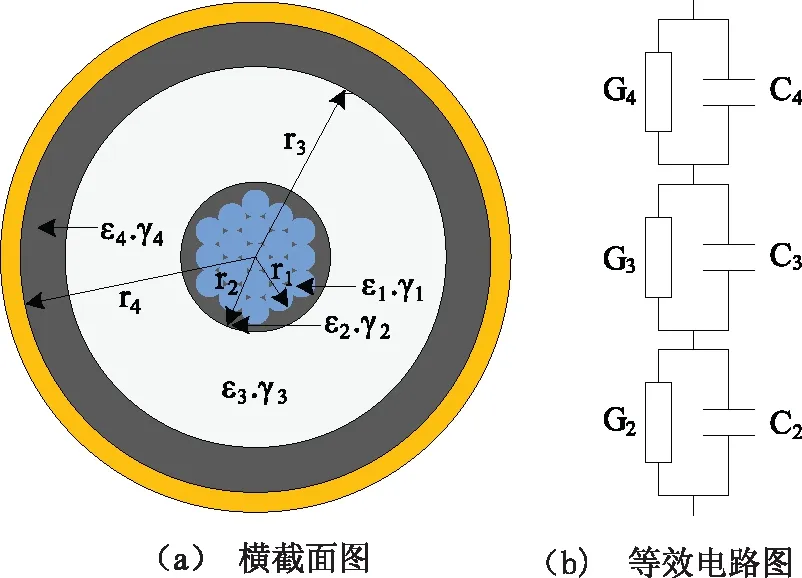
图2 无水树电缆模型
如图2(a)所示的横截面中,εi和γi(i=1~4)分别为第i层的相对介电常数和电导率。如图2(b)所示的等效电路中,G2和C2分别为内半导电层的电导和电容;G3和C3分别为XLPE绝缘层的电导和电容;G4和C4分别为外半导电层的电导和电容。
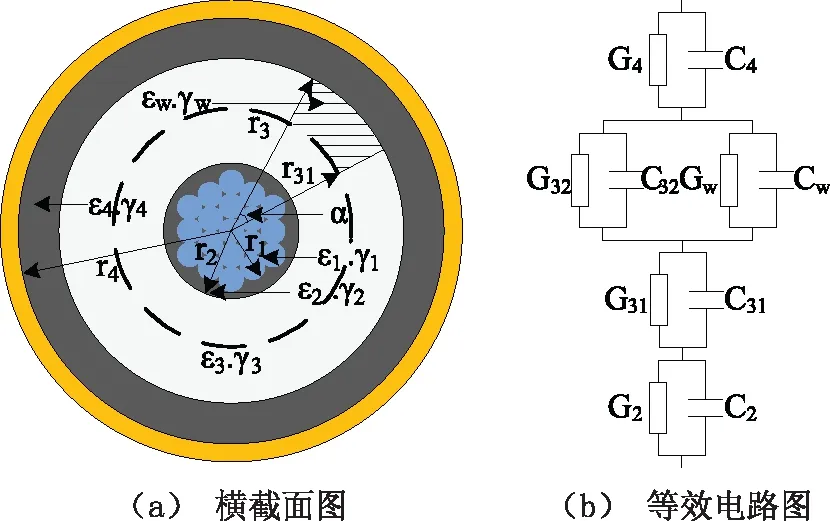
图3 有水树电缆模型
如图3(a)所示的横截面中,将水树区域等效为一夹角为α的扇形,εw和γw分别为水树部分的相对介电常数和电导率。如图3(b)所示的等效电路中,G31和C31分别为XLPE绝缘层半径介于r2和r31环状无水树区域的电导和电容;G32和C32分别为XLPE绝缘层半径介于r31和r3之间,夹角为π-α环状无水树区域的电导和电容;Gw和Cw分别为XLPE绝缘层半径介于r31和r3之间,夹角为α扇形有水树区域的电导和电容。
1.2 电缆的等效电路参数
为了分析有、无水树电缆的等效电路参数值的区别,以及对电缆绝缘状态的影响。本文基于电路理论公式推导长度为L电缆的等效电路参数。其中各层及整体的电导值为[18]:
(1)
式中Gi(i=2~4)分别为第i层的电导,ri(i=1~4)分别为第i层的半径。
(2)
式中Gs为多层电导的串联总电导。
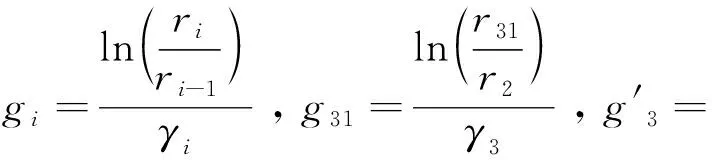
则无水树和有水树电缆的电导分别为:
(3)
(4)
同理可得,电缆各层及整体的电容值为:
(5)
式中Ci(i=2~4)分别为第i层的电容,ri(i=1~4)分别为第i层的半径。
(6)
式中Cs为多层电导的串联总电导。

(7)
(8)
通过比较式(3)和式(4),可以得出有水树电缆的电导比无水树的大,即有水树电缆的等效电阻小于无水树电缆,绝缘水平较低;比较式(7)和式(8),有水树电缆的电容比无水树的大。而实际电缆中有水树部分电缆占整段电缆长度比重很小,如若将每段电缆视为RC并联模型,整段电缆就由多个RC并联模型组成。整体等效电阻受水树部分的等效电阻影响较大,即影响着电缆的绝缘状态。
2 评估方法及理论证明
水树的存在将使得电缆等效电路参数的等效电阻值变小,而实际中水树的存在会使得电缆的绝缘强度降低,即等效电阻值与绝缘状态存在同向变化的相关性。所以在上述RC并联等效电路模型的基础上,施加冲击电压u(t)于电缆上,利用电缆上的冲击电压u(t)及对应的冲击电流i(t),提出一种新的方法评估电缆的绝缘状态。首先,从能量的角度,定义有功损耗为:
(9)
冲击电压u(t)下的冲击电流i(t)为:
(10)
将式(10)代入式(9)得:
(11)
因为u(0)=0,u(∞)=0,所以:
(12)
(13)
式中R为短电缆的整体等效电阻;C为短电缆的整体电容;W为有功损耗。
由式(13)可得电阻值为:
(14)
通过式(14)可得到电缆等效电路中等效电阻值,从而可以通过它对电缆的绝缘状态进行评估。其依据应为等效电阻值越大,即绝缘性能越好,反之亦然。对实际电缆进行评估时,可通过横向和纵向比较的方法对电缆绝缘性能进行评判。将新电缆的初始等效电阻值作为基准,在后续测试中将电缆的等效电阻值与基准值相比较。如若没有新电缆的初始等效电阻值,可对比同一批次或同一线路的三相电缆的等效电阻值[19]。如果需要确切的数值,也可以通过成熟的评估方法进行验证,得出合适的评判标准[20]。
3 结果与分析
为了验证电缆等效电阻值的理论计算公式的正确性,利用ATP模拟不同电阻值的电缆参数进行仿真,基于式(14)通过MATLAB计算得到等效电阻值,并对比仿真设置的电阻值与计算所得等效电阻值。
建立短电缆RC并联等效电路模型,并加入了冲击电压发生器的等效电路,整体的电路原理图如图4所示。通过设置不同的电阻、电容值,模拟不同长度和不同绝缘状态的电缆。实测10 cm长的短电缆电容值在40 pF~70 pF之间,电阻值为GΩ级。因此,选取电容值分别为50 pF和100 pF,电阻值分别为0.1 GΩ、1 GΩ、10 GΩ、100 GΩ进行仿真。

图4 仿真电路图
仿真得到如图5所示的冲击电压波形和冲击电流波形。

图5 冲击电压和冲击电流波形
从图5可以得出,冲击电压与冲击电流的起始时刻相同,且起始和终止值均为零,无工频电压与电流的角度差。冲击电流波形不同于冲击电压波形,冲击电流波形的前面部分为正,后面部分为负;冲击电流峰值时间位于冲击电压峰值时间的前面,冲击电压峰值时间位于冲击电流过零时间的前面。
利用式(14)计算不同仿真数据结果,得到冲击电压下不同等效电阻值计算结果。其中表1为仿真电容值为50 pF时,不同仿真电阻值和计算等效电阻值的数据;表2为仿真电容值为100 pF时,不同仿真电阻值和计算等效电阻值的数据。

表1 50 pF电容时电缆的电阻值

表2 100 pF电容时电缆的电阻值
从表1和表2可以得出,不同电容值时,仿真设置的电阻值与理论计算的等效电阻值之间误差最大为0.4%。即基于冲击电压下电缆等效电阻值的计算方法是可行的,能够作为评估电缆绝缘状态的一种新的方法。
4 结束语
文章通过建立电力电缆的RC串并联等效电路模型,给出了电力电缆各层及整体的等效电路参数,提出了一种基于冲击电压下电缆等效电阻值的计算方法,理论推导出了其计算公式,并得出利用等效电阻值的大小评估电缆绝缘状态的新方法。仿真计算结果表明,该计算方法所得等效电阻值的结果与仿真设置电阻值之间的误差小于0.4%,在误差的可接受范围内,表明该方法是可行的。

