基于新型标准数字功率源的数字化电能表检定和溯源方法
宋晓林,任伟,邵方静,谢静,曾翔君
(1. 国网陕西省电力公司电力科学研究院,西安 710100; 2.西安交通大学,西安 710048;)
0 引 言
数字化电能表是应用于数字化智能变电站的计量装置,与传统模拟式电能表不同,其输入信号为符合IEC 61850协议标准的数字报文[1-2]。因此数字化电能表的溯源和检定方式法与传统模拟电能表不同[3]。黑龙江省电力科学研究院针对这一问题提出了一种数字电能计量系统整体校验法如图1所示,传统标准电能表校验仪直接对标准电流互感器和标准电压互感器输出的二次信号进行采样计算,得出标准电能值。然后通过与数字电能表发送的电能脉冲进行比较得到数字电能系统的电能计量误差。该方法实现了数字电能计量系统(包含电子式互感器、合并单元、数字化电能表等)的检定,但未解决对数字化电能表单独进行量值溯源和检定的难题[4]。
目前国内某单位针对数字化电能表的溯源与检定提出了两种方法[2]:
方法一:标准数字电能表比较法的框图如图2所示。在该方法中,将符合IEC 61850协议标准的数据帧同时输入标准数字电能表和被检数字电能表,然后直接比较电能计量结果得到被检表的误差。这种检定方法的优点是操作简便,但是该方法中的标准数字电能表本身的溯源尚未解决,这又回到了溯源方法的问题[5]。
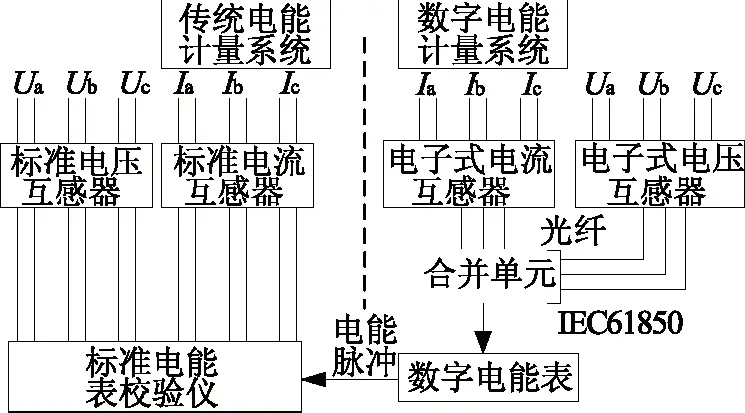
图1 数字电能计量系统整体校验法
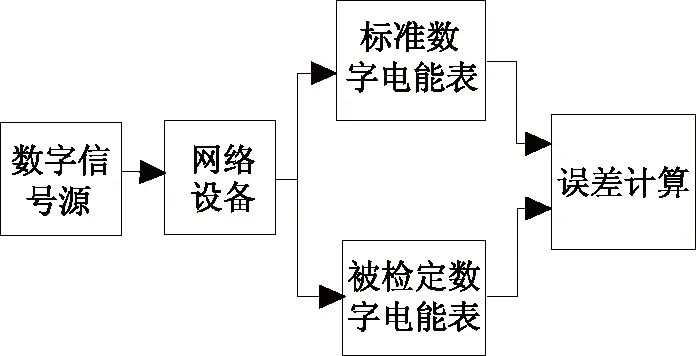
图2 标准数字电能表比较法
方法二:标准数字功率源法的框图如图3所示。在该方法中,标准数字功率源输出符合IEC 61850协议标准的数据帧,并且该数据帧所代表的电压、电流信号的幅值和相位可以根据实际要求设置。根据标准数字功率源的的参数得到理论电能值,与被测表的计量结果比较就可以得到被检表的误差。该检定方法的优点是结构简单,但是由于数字功率源的输出并非真正的电信号,不具备电能标准特性,不能直接向上溯源,该方法受到了业界人士的质疑[6-7]。
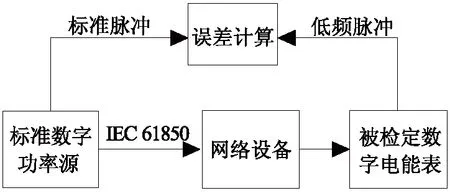
图3 标准数字功率源法
数字化电能表实际上处理的是没有量纲的数值,因此可以通过图3给出的方法对数字化电能表单独进行溯源和检定,但不是量值溯源,而只是数值溯源。另外,这种传统数字功率源输出的是基于标准正弦波的数据,忽略了实际测量系统中由截断误差、模拟噪声和谐波功率造成的不确定度。本文首先论述了数字化电能表数值溯源方法的理论据;进而针对传统标准源法在实际应用中存在的问题给出了详细的描述;最后提出了一种新型的标准数字功率源法,可以有效地解决数字化电能表的检定和溯源问题。
1 数字化电能表的数值溯源及传统标准数字源法存在的问题
数字化变电站计量系统的结构如图4所示[8-9],电子式互感器将一次电压和电流通过光学或其它方式传感后转换为数字量,即把模拟信号采样离散化成数字序列(A/D转换),然后对数字序列进行数字信号处理,得到输出序列。
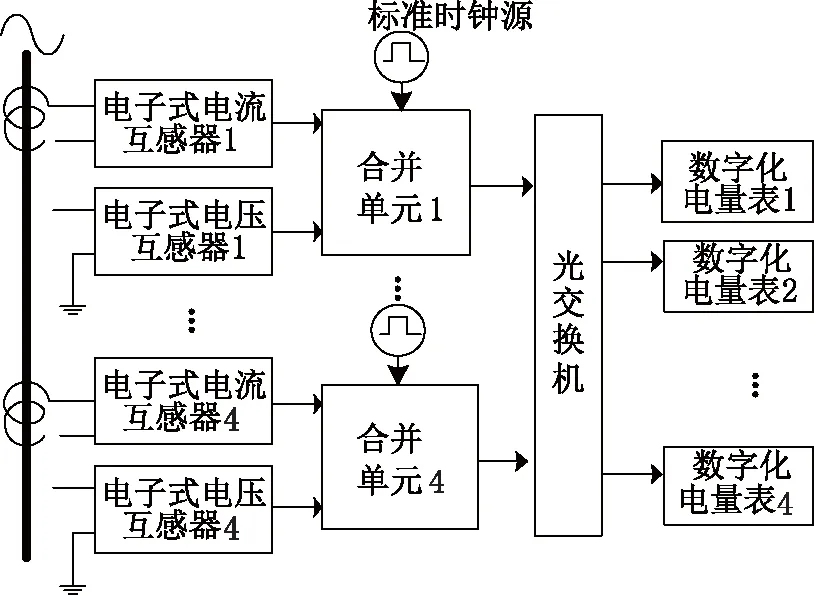
图4 数字化变电站计量系统的结构示意图
其中,A/D转换过程的输入—输出关系式为:
最后得到:
(1)
式中D为A/D转换结果;udn为量化噪声以及模拟噪声对应的模拟量;d为量化噪声以及模拟噪声对应的数字量。Ui为输入电压,N为转换位数,Uref为参考电压。由式(1)知,A/D转换过程的输出是一个没有单位的数字量,所以A/D转换之后都不存在量的溯源问题。由量化噪声和模拟噪声产生的误差将以数字量d的形式传递到数字化电能计量系统中去。
合并单元采用一个标准的时钟源作为输入,并对采样的数据进行汇总。从合并单元输出的数字序列通过通讯系统传送给数字化电能表。数字化电能表的实质是数值处理,只接收没有量的数值。因此数字化电能表的溯源分为数值溯源和量的溯源两个部分。因为在整个计量系统中始终存在误差传递,例如模拟电路产生的噪声、电力系统中的谐波都会转换成数字量传递给数字化电能表进而影响电能计量的准确度,所以应对数字化电能表单独进行数值溯源。若要进行物理量溯源,则必须对数字电能计量系统的整体(包含电子式互感器、合并单元、数字化电能表等)进行溯源,只要实现了参考电压Uref的量的溯源就实现了数字电能计量系统的量的溯源。
数字化电能表实际上处理的是没有量纲的数值,因此可以通过标准数字功率源法对数字化电能表单独进行数值溯源和检定。传统标准数字功率源输出的信号是基于标准正弦信号产生的数据帧,具有周期重复性,不具有A类不确定度。这种做法忽略了实际测量系统中由截断误差、模拟噪声和谐波功率造成的不确定度,无法模拟实际测量系统中的不确定性。
另外,由于数字功率源数值精度的限制,理论功率值本身具有B类不确定度。一旦设定了标准数字功率源输出的数据帧所代表的电压、电流信号的幅值、相位和频率,相应的功率理论值就是一个精确的定值。这就使得制造商有机会通过调整被检表的算法对电能计量结果进行适当的修正,使其与理论电能值完全一致,从而掩盖了电能表本身的算法误差。看似B类不确定度得到了修正,但在实际测试环境中由于各种影响量的引入,被检表的测量准确度将有不同程度的下降。所以基于标准正弦波的数字功率源检定法存在不严谨之处。
2 基于新型标准数字功率源的检定方法
2.1 检定方案概述
针对数字化电能表的检定,本文提出了一种基于新型标准数字功率源的检定方案如图5所示。根据标准数字化电能表只有数值溯源而不存在物理量的溯源以及理论值即真值的观点,将三角函数形式的傅立叶级数与随机函数相加所得的复合函数作为新型标准数字功率源的输出形式,这就可以通过调节随机函数的参数来改变数字功率源的B类不确定度。
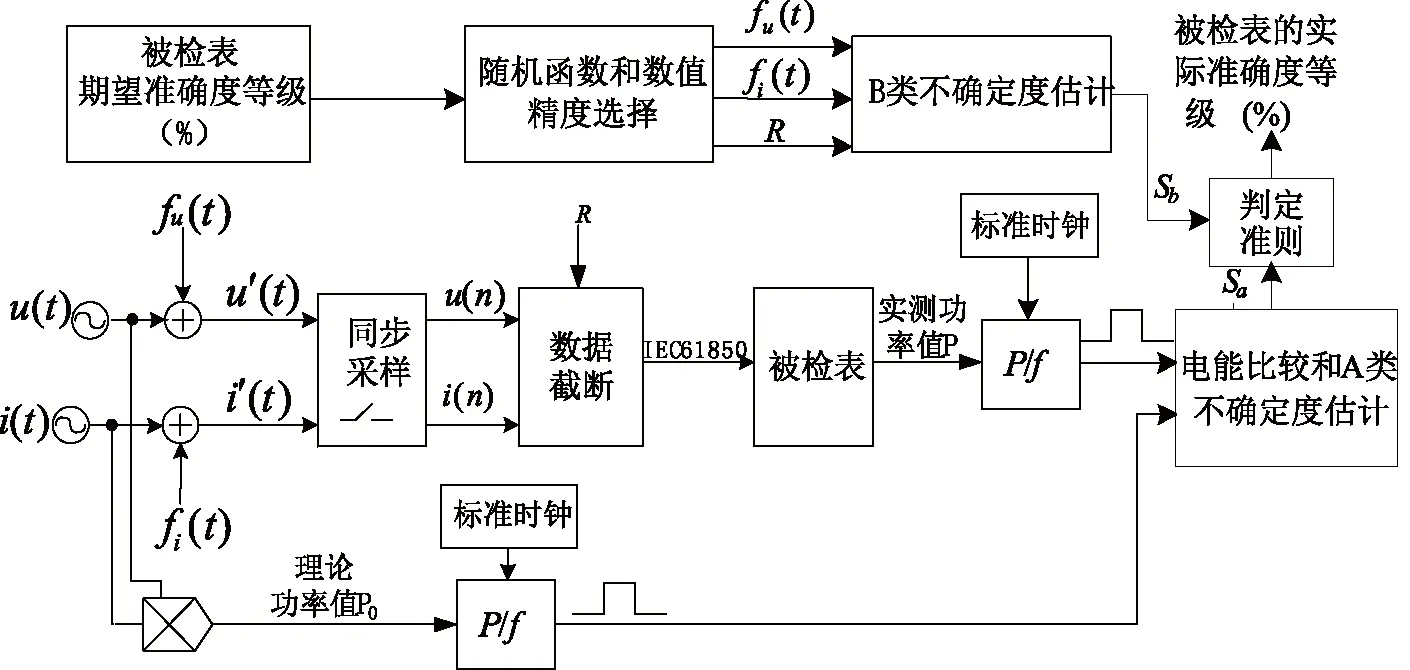
图5 推荐的检定方案
具体检定步骤如下:
(1)在给定标准数字功率源的理论功率P0的情况下,根据被检数字化电能表的期望准确度等级来确定数值精度R和随机函数fu(t)、fi(t)的参数;
(2)由标准数字功率源产生傅里叶级数形式的三角函数u(t)和i(t),分别与随机函数fu(t)、fi(t)相加得到复合函数u′(t)和i′(t);把u′(t)和i′(t)送入同步采样模块,再经过数据截断得到离散值u′(n) 和I′(n);同时,数据截断和随机函数的引入使测量结果产生B类不确定度Sb;
其中,u′(t)和i′(t)的表达式为:
(2)
式中角频率ω、初相位φu和φi均可调;φu和φi要保持恒定的相位差,即φu-φi=Ф;Un和In为电压、电流的n次谐波幅值;理论功率值P0的表达式为:
P0(t)=u(t)×i(t)
(3)
(3)基于IEC 61850通信协议把离散值u′(n)和i′(n)发送给被检数字化电能表;
(4)将被检数字化电能表输出的实测功率值P和理论功率值P0同时送入P/f模块,通过电能比较得到被检数字化电能表的A类不确定度,根据合成不确定度判定被检数字化电能表的实际准确度等级。
2.2 数值精度的选择和检定规则
数据截断会引起截断误差并传递给被检表的测量结果,产生B类不确定度对测量准确度造成影响。即使计算方法准确,也不能得到真值,所以对不同等级表检定时必须对数值精度进行规定。输入数字表的数值精度取决于A/D采样精度和数据存储位数,与被检表自身的准确度无关。
截断误差类似AD转换过程中产生的量化误差。截断误差的分布是一个周期锯齿波如图6所示。
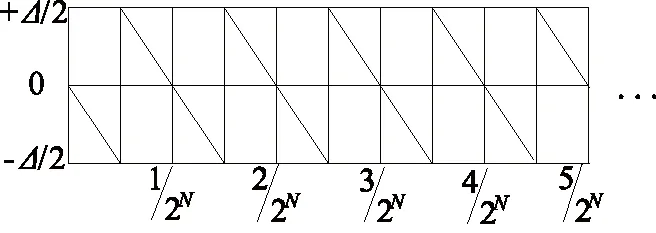
图6 截断误差分布
其幅度范围是[-Δ/2,+Δ/2],Δ=1/2N,N为数据存储的位数。截断误差f(x)的复指数傅立叶级数为:
(4)
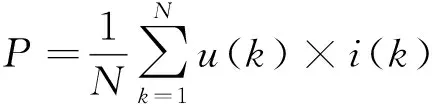

表1 不同数值精度数据引起的扩展不确定度
所以对不同准确度等级的数字表检定时应该采用不同数值精度的数字源,选择的依据见表2。校验步骤分为2步。
步骤1:严格按照表2的规则选择数值精度足够的标准数字功率源作为被检数字化电能表的输入,评估被检数字化电能表的测量不确定度。例如,对期望准确度等级为0.02级的数字化电能表定级时,只能选择32位、24位或16位数值精度的数字化功率源作为被检数字化电能表的输入。若被检数字化电能表的测量结果相对真值的不确定度S≤0.02%,则进行步骤2校验;否则认为不能达到期望的准确度等级。
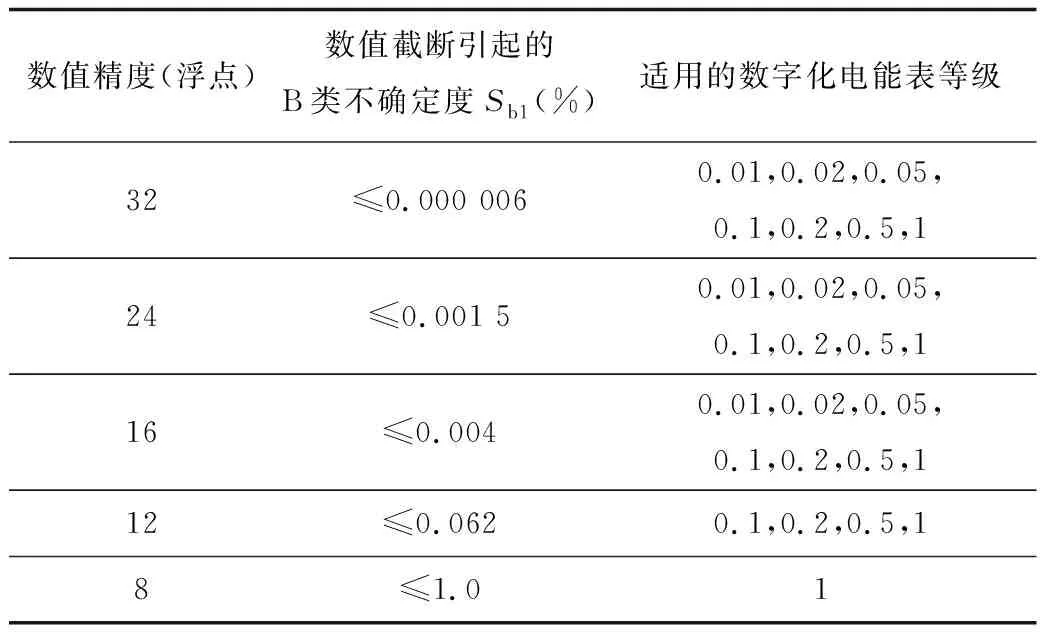
表2 数字源数值精度的选择依据
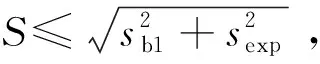
经过上述2步校验,满足条件的被检数字化电能表被判定为达到期望准确度等级,否则认为不能达到期望的准确度等级。
2.3 随机函数的选择与检定规则
实际信号在采样过程中会引入各种模拟噪声,产生B类不确定度,传递给离散化后的瞬时电压、电流值,从而对被检数字化电能表的测量准确度造成影响。由噪声引起的B类不确定度与被检数字化电能表自身的准确度等级无关。本文采用随机函数来模拟实际信号采样过程中引入的各种形态的噪声,并根据被检数字化电能表的准确度等级来设置随机函数的参数。
随机函数f(t)的选择应满足以下两个基本条件:(1)随机函数f(t)的平均值为0,方差可调;(2)随机函数f(t)与正弦函数的相关系数为0(不产生功率)。集成电路的主要噪声形态为高斯白噪声和1/f噪声。
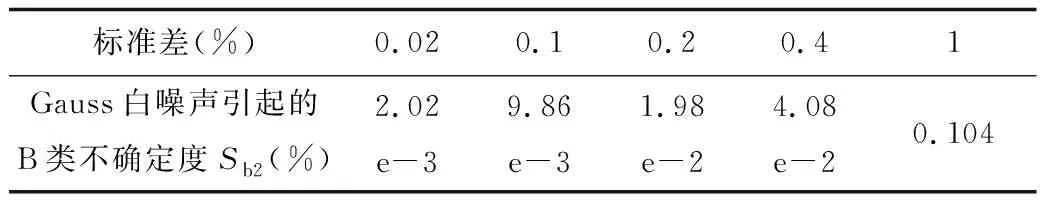
表3 不同标准差的Gauss噪声引起的B类不确定度

表4 不同标准差的1/f噪声引起的B类不确定度
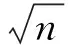
所以施加这两种随机函数时,标准差的大小应根据被检数字化电能表的期望准确度等级设置,设置依据见表5、表6。
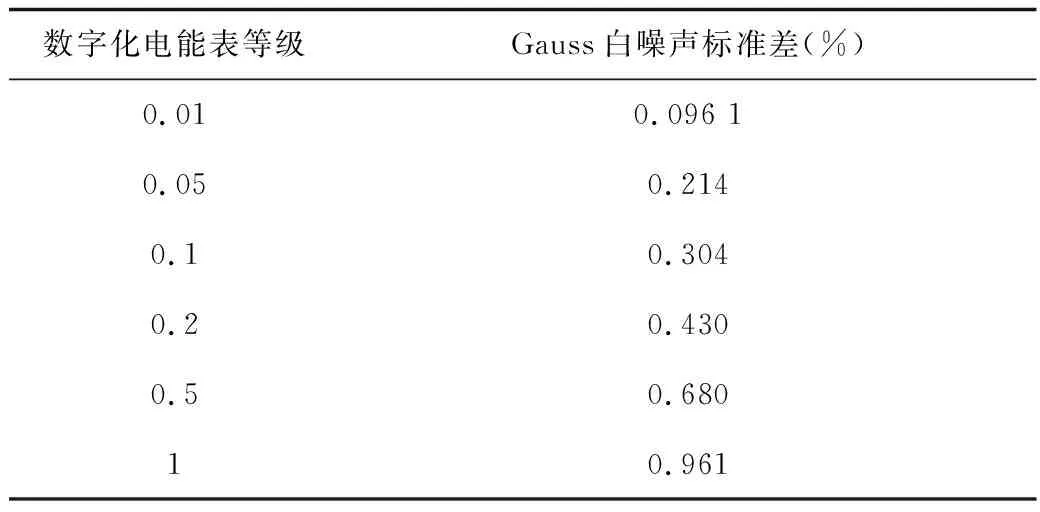
表5 高斯白噪声标准差的设置容限
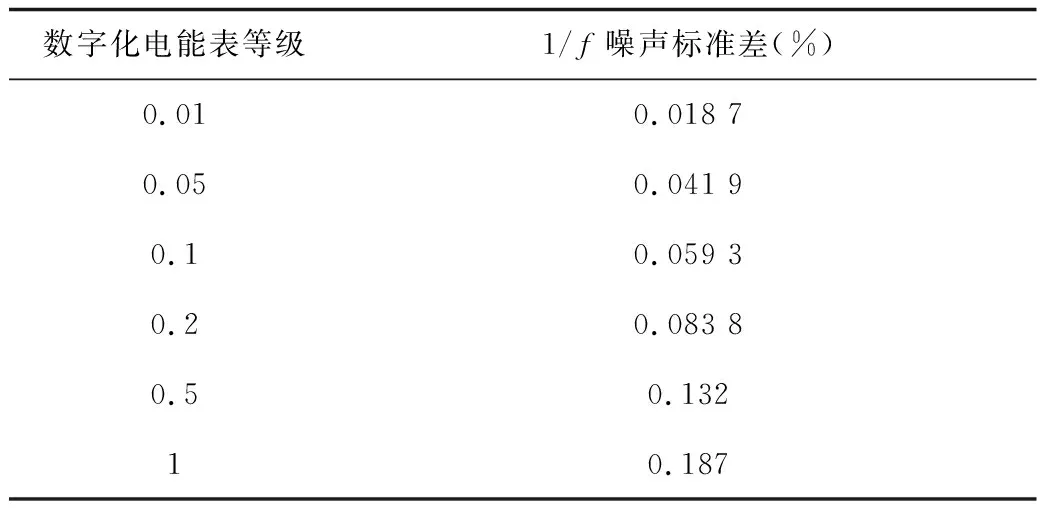
表6 1/f噪声标准差的设置容限
检定过程中施加的随机函数f(t)是满足上述规则的任何形式的随机函数的线性组合,f(t)的表达式为:
f(t)=d1×f1(t)+d2×f2(t)+d3×f3(t)+…
(5)
式中f(t)为检定过程中施加的随机函数;f1(t)、f2(t)、f3(t)...为满足上述规则的任何形式的随机函数,数值精度为32位;d1、d2、d3……为组合系数。在合成不确定度符合要求的前提下,组合系数可自行决定,本文不作要求。
校验步骤:
步骤1:施加随机函数的标准差小于等于表5、表6中的容限,评估被检数字化电能表的测量不确定度。例如,对期望准确度等级为0.1级的数字化电能表定级时,选择标准差δ≤0.304%的Gauss白噪声或标准差δ≤0.059 3%的1/f噪声与标准数字功率源复合。若被检数字化电能表的测量结果相对真值的不确定度S≤0.1%,则进行步骤2校验;否则认为不能达到期望的准确度等级;
经过上述2步校验,满足条件的被检数字化电能表被判定为达到期望准确度等级,否则认为不能达到期望的准确度等级。
2.4 谐波的选择与检定规则
实际电力系统中的谐波会产生功率波动,对电能表的测量准确度带来影响。谐波影响下电能表实测电能值与时间的关系曲线图如图7中蓝色实线所示,没有谐波影响下的理论电能值与时间的关系曲线如图7中黑色虚线所示。易见t1至t2时刻的实际累计电能值E2大于理论累计电能值E1,所以谐波对数字化计量系统的影响不可忽略,检定数字表时应施加不同频率的谐波以考察数字表的滤波性能。
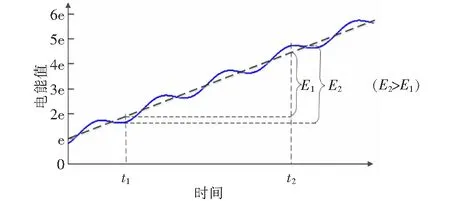
图7 谐波影响下累计电能值与时间的关系曲线
考虑到谐波电流的影响,基波电流的表达式为:i(t)=Aisin(2π×f0×t+φi),基波电压的表达式为:u(t)=Ausin(2π×f0×t+φu),频率为fp的电流谐波的表达式为:ip(t)=Aipsin(2π×fp×t+θ)。则瞬时功率的表达式为:
p(t)=u(t)×(i(t)+ip(t))=
cos(2π(f0+fp)t+φu+θ))
(6)
式中有1个直流项和3个交流项,直流项即理论功率值。施加不同频率的谐波时,造成谐波功率的主要项是式(6)中的第3项,根据滤波器的幅频特性可确定施加谐波的衰减比进而确定施加谐波的最大幅值。
检定数字化电能表时施加谐波的最高次数应满足采样定理的要求。以准确度等级为0.02级的数字化电能表为例,施加谐波的幅值应不超过图8给出的要求。其中Am是电流谐波幅值Aip与电流基波幅值Ai之比,Am=Aip/Ai,Δf为谐波频率fip与基波频率f0的差,Δf=fip-f0。在满足采样定理的条件下,当Δf>100 Hz时,施加谐波幅值不应超过基波幅值。
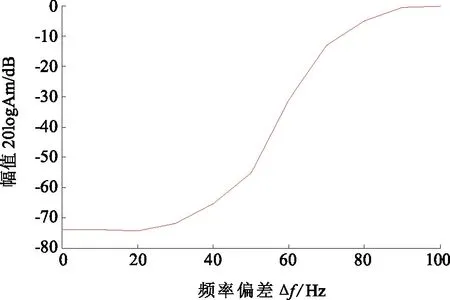
图8 施加谐波的幅频特性
对其他等级电能表进行检定时,施加谐波的幅频特性曲线的形状与图8类似,表7给出一些典型频率的谐波对应的幅值要求。

表7 施加谐波的幅值要求
3 实验结果与分析
采用本文提出的检定方案分别对4个不同厂家生产的准确度等级均为0.2S级的数字化电能表进行检定,且这4个数字表采用传统检表法的检定结果均为合格。
(1)施加随机函数的检定结果
由于集成电路中的首要噪声形态为高斯白噪声,本次实验过程中施加不同标准差大小的高斯白噪声形态的随机函数并记录数字化电能表的功率测量结果。4个数字表有功测量的相对不确定度如表8所示。
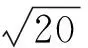
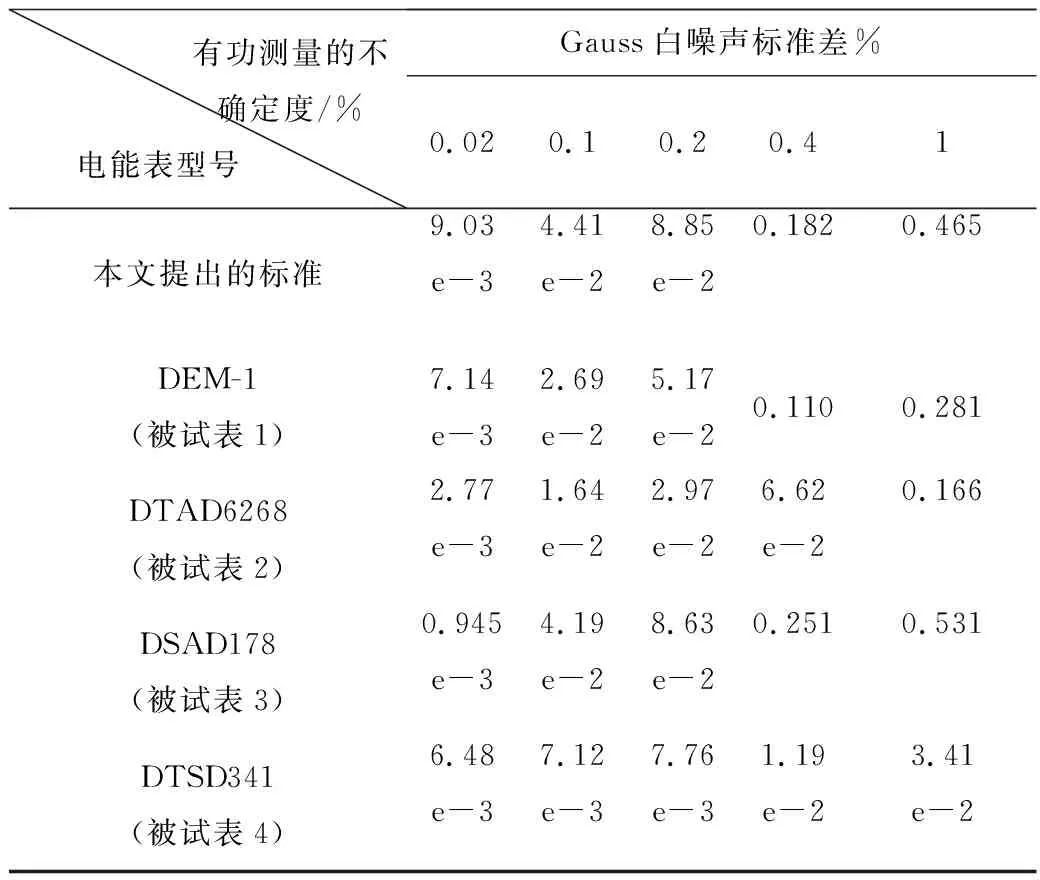
表8 施加随机函数的检定结果
(2)施加谐波的检定结果
由2.3节可知,造成有功功率波动的主要谐波频率范围为50 Hz 由图9可知,被试表4的滤波性能最优,施加100 Hz以上谐波的幅值可达到基波幅值的100%。被试表1在各个频点处的滤波性能较好,满足本文提出的滤波性能要求。被试表3对5 Hz的倍频谐波的滤波效果突出,对低频谐波的滤波效果较好,能够满足要求;但对120 Hz以上的谐波滤波效果较差,不满足本文提出的要求。被试表2对50 Hz的倍频谐波的滤波效果突出,但对105 Hz以上的谐波滤波效果较差,不满足本文提出的要求。所以按照2.4节提出的校验步骤进行检定,被试表1和4被判定为能达到期望准确度等级0.02级,被试表2和3被判定为不能达到期望准确度等级0.02级。 图9 施加谐波的幅频特性 另外,4个被试表均采用数值精度为32位的数据帧计算分析,符合表2中提出的0.02级数字表应满足的数值精度要求。 由本次实验结果可知被试表4具有较好的滤波性能和噪声抑制性能,它在不同噪声和谐波环境下有功测量的相对不确定度均小于其他三个被试表。在实际应用中也证实了被试表4的可靠性最高,受到了业内人士的广泛认可。本文讨论的检定方法区别于传统检表法能够鉴别出不同厂家生产的数字化电能表的性能优劣,较科学地实现了对数字化电能表的检定。另外,目前我国国家标准规定数字化电能表的最高准确度等级为0.2S级,本节实验中所采用的四个数字化电能表在整体校验方案中均被定级为0.2S级,但不表示数字化电能表本身的准确度不能达到更高的准确度等级,这是由于在整体校验中得到的电能计量误差不仅包括数字表本身的不确定度还引入了电子式互感器的测量不确定度。 首先,本文相对科学地解决了关于数字化电能表溯源问题的困惑,指出数字化电能表的实质是数值处理,只存在数值溯源,而不存在量的溯源的问题。如果要进行电能计量量值溯源,则必须对数字化电能计量系统的整体进行溯源。进而本文针对传统标准源法在实际应用中存在的问题给出了详细的描述,最后针对数字化电能表的检定和量值溯源问题提出了一种新型的数值精度可调的标准数字功率源模型,即将三角函数形式的傅立叶级数与随机函数相加所得的复合函数作为标准数字功率源的输出形式,包含了实际测量系统中的模拟噪声和谐波功率。本文详细规定了不同情况下新型数字功率源的数值精度、施加的随机函数和谐波的设置规则以及检定步骤。这种基于新型标准数字功率源的方法可以有效地解决数字化电能表的检定和溯源问题,在实际应用中有待进一步优化。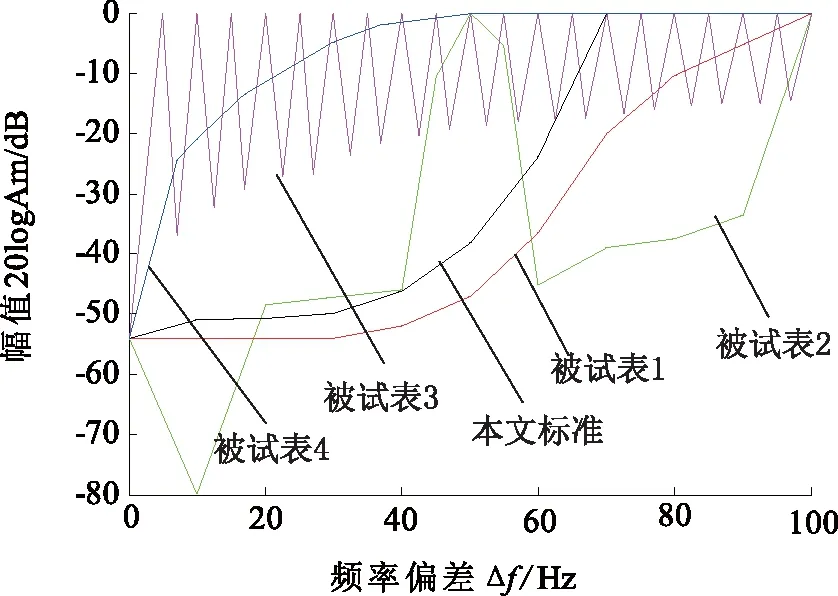
4 结束语

