基于VMD的谐波检测方法
陈强伟,蔡文皓,孙磊,牛春光
(西安科技大学 电气与控制工程学院,西安 710054)
0 引 言
近年来由于电力电子器件的发展,使得大量的非线性负载运用到电网中,由此引起的电能质量问题得到了社会的广泛关注,而谐波对于电网的污染首当其冲[1-3]。随着新能源在电力的快速发展,使得各种分布式电源应运而生,比如光伏发电、太阳能发电和风力发电等等,这些小型的发电设备并网运行时,同样也给电力系统带来了一系列的谐波污染问题[4]。
谐波污染问题会给电网带来各种不良的结果,其中最为重要的表现如下:谐波谐振会使得电力系统过电压,造成电力网络中的电气元件老化与损毁;增加发电机系统额外的谐波损耗和发热,大大缩短了发电机的运行时间;在继电保护中会使得敏感的电气保护元件误动和拒动;对通信设备产生电磁干扰,将很大程度上减弱了通信质量[5]。
一直以来,许多学者专家关于谐波检测问题进行了大量的探索与研究,提出了一系列谐波检测的有效方法。具体方法有:瞬时无功功率理论(p-q和ip-iq)算法[6-7]、Fryze功率理论算法[8]、傅里叶变换算法[9-10]、小波变换算法[11-12]、自适应滤波算法[13-14]、神经网络算法[15]、经验模态分解[16-18]等算法。瞬时无功功率理论算法虽然能准确的检测出谐波分量,但是实现方法数学公式较多,实现困难,并且要求电网电压无畸变这一理想条件。Fryze功率理论算法同样是要求电网电压无畸变这一理想条件。而傅里叶算法只在信号稳定时检测结果较为精确,但在非稳定信号傅里叶算法并不能检测出来。虽然小波变换算法恰好克服了傅里叶变换的缺点,但是小波变换要对小波基函数进行选择,不同的小波基函数所检测出来的谐波分量也有一定的影响。自适应滤波算法和神经网络算法需要大量的检测样本这一前提条件,并且自适应滤波算法的迭代步长不太好控制。EMD虽然实现简单,但是得到的模态函数容易产生虚假分量和模态混叠。在上述方法进行谐波检测之中,有许多算法需要用到低通滤波器来提取基波分量,然后用待检测信号减去基波信号得到所要检测的谐波分量。显然,低通滤波器对检测结果准确性有着一定的关系。
VMD是一种新提出的对信号进行时频变换的方法[19],它的分解结果与EMD有着相似之处,但是它与EMD算法的原理截然不同。VMD算法通过迭代搜索变分模型最优解以此来提取每一个分量的中心频率及带宽,从而得到本征模态分量。同时VMD算法可以抑制噪声和冲击信号所引起的模态混叠这一不利因素。VMD算法已成功的运用到风电机组故障诊断[20]、机械故障诊断[21]、变压器的放电去噪[22]中。本文首次将VMD算法运用于电网的谐波检测当中,通过VMD算法将含有谐波分量信号分解为本征模态分量,然后对每一个本征模态分量进行Hilbert变换,找出基波的幅值和频率参数,最后将电力待测信号减去所提取的基波信号,即可检测出电力网络的谐波。该方法对电网的电压没有任何要求,在实现过程中也无需用到低通滤波器,所检测出来的谐波具有很高的精度。
1 变分模态分解算法
VMD算法是由加利福尼亚大学的Konstantin Dragomiretskiy等人2014年提出的一种新的可变尺度信号分解方法。VMD算法是利用迭代搜索变分模型最优解的方式来提取每个IMF分量,它可以把一个复杂的信号分解为K个IMF分量信号,因为K值是我们自己选定的,如果K值取得合适,那么就可以避免待检测信号由于模态混叠现象而给分解带来的不利影响。
1.1 本征模态分量
对于任意个IMF分量都可以看成是一个调幅-调频信号,其可表示为:
uk(t)=Ak(t)cos(φk(t))
(1)
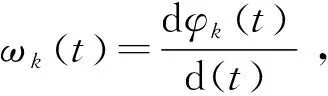
1.2 变分模型
VMD算法的核心是将一个待检测信号x分解成许多个本征模态分量uk(t),这些uk(t)可以通过如下方式计算得到:
(1)对uk(t)进行Hilbert变换,就可以获得uk(t)的解析信号,从而计算出uk(t)的单边频谱。
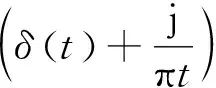
(2)
式中δ(t)为单位脉冲函数;j为虚数单位;*表示卷积。
(2)对模态分量uk(t)的解析信号估计它的中心频率e-jωkt,然后将每一个uk(t)的频谱调制到与它相对应的基频带。
(3)
(3)最后计算式(3)解调信号的梯度的L2范数的平方。
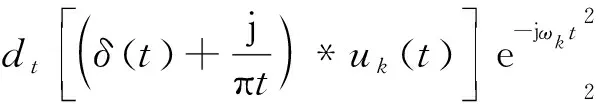
(4)
式中dt为函数对时间t的偏导数。
通过步骤 (1)~步骤(3)得到变分约束模型为:
(5)
式中uk={u1,u2,…uk}为模态的集合;ωk=(ω1,ω2,…ωk)为相对应中心频率的集合。
上述变分约束模型实际上是一个约束的最优化问题,为了求解上述优化问题,利用二次惩罚项和拉格朗日乘子法引入增广Lagrange函数η。
1.3 变分模型的求解
对于式(5)引入增广Lagrange函数η后可得:
η({uk},{ωk},λ)=
(6)
式中α表示罚参数;λ为Lagrange乘子。
利用交替方向乘子算法求解式(6)变分模型增广Lagrange函数η的最优解。
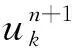
(7)
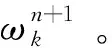
(8)
将公式(8)转换为非负频率区间积分的形式:
(9)
则变分问题的解为:
(10)
同样求得中心频率ω(k)的更新为:
(11)
其中迭代停止准则 :
(12)
从对求解步骤来看,VMD算法是将每一个本征模态分量直接在频域上在更新结束后满足停止准则的前提做一系列的更新。
2 基于VMD的谐波检测
根据前面第1节所述的变分模态分解算法,将电网的待测电流作为复杂信号x。接着按以下步骤:

(2)对于n=n+1执行整个迭代;
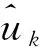
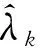
(13)
式中γ代表噪声容限参数。为了分解结果不受噪声影响,可让γ=0。
(5)循环步骤(2)~步骤(4)直到当满足式(12)的迭代停止准则。
3 算例仿真和实测数据分析
3.1 算例1
假设在一个含有谐波的电流信号为:
x(t)=100sin(100πt)+30sin(300πt)+
20sin(500πt)+10sin(700πt)
(14)
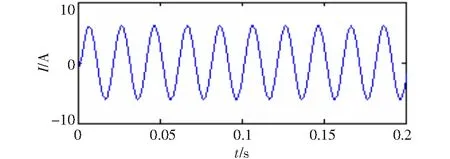
由式(14)可知该电流信号一共含有四种成份,公式的第一项为电流的基波成份,并且幅值为100,频率为50 Hz。公式的后三项分别为3次、5次和7次谐波,其幅值分别为30、20、10。电流信号的采样频率为5 000 Hz,采样点数为5 000(这里取前2 000个点)。图1是该电流信号的原始波形图。对x(t)分别进行VMD和EMD分解,获得的IMF如图2和图3所示。
由图2可知,VMD分解能够很清晰的分解出含有谐波的电流信号的四种分量,使得分解结果很合理。而图3 EMD分解出来的四种分量,虽然50 Hz和150 Hz的分量能够清晰的分解出来,但是对于250 Hz和350 Hz的分量的分解不尽理想,分解出来的也不是正弦波,误差很大。EMD分解的不合理是因为所假设的谐波的电流信号存在严重的模态混叠现象,而VMD分解能抑制模态混叠现象,所以二者的分解结果存在着差异。现在单独对这两种分解结果下的基波做Hilbert变换。图4和图5分别代表了VMD和EMD分解下基波的Hilbert变换。
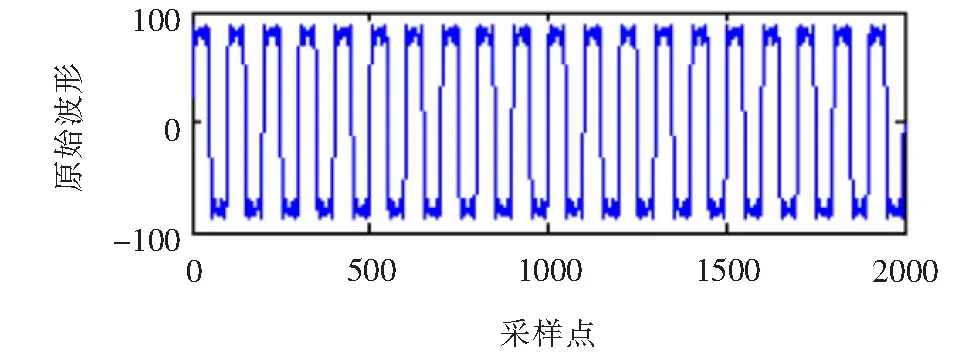
图1 谐波信号
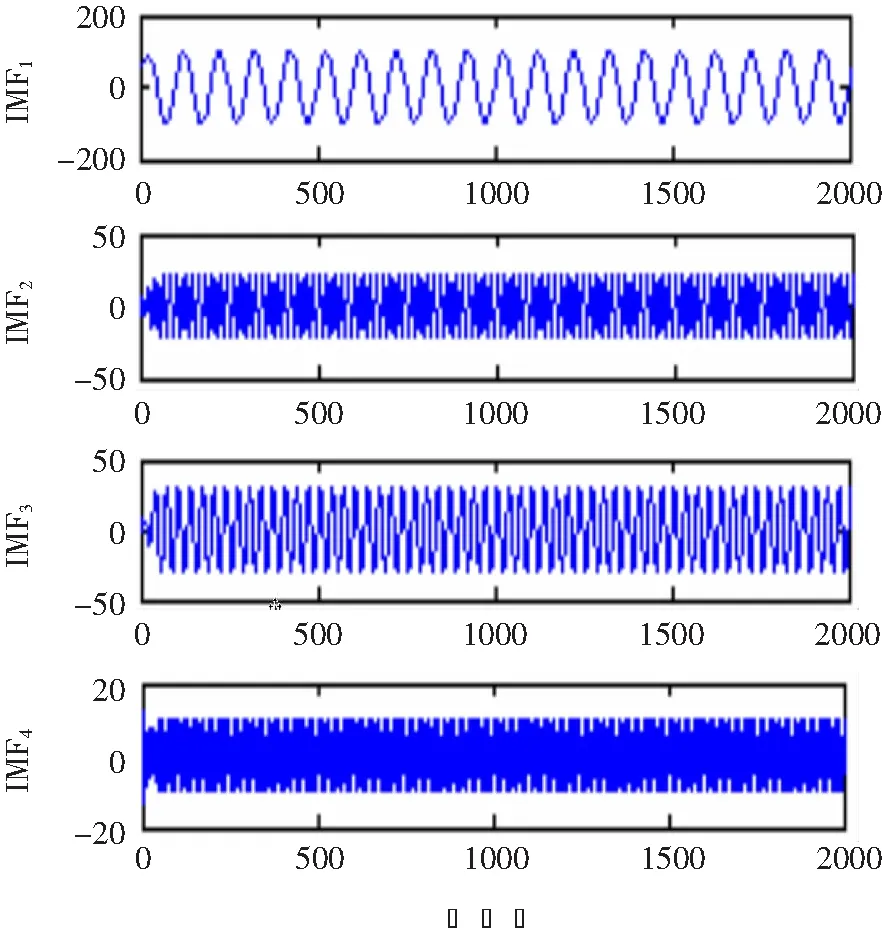
图2 VMD分解结果
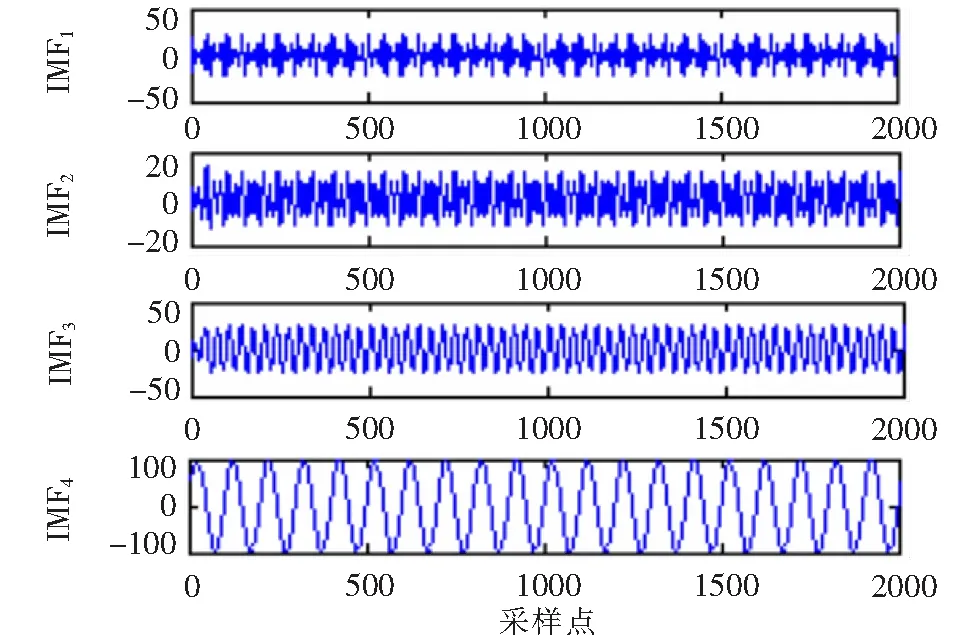
图3 EMD分解结果
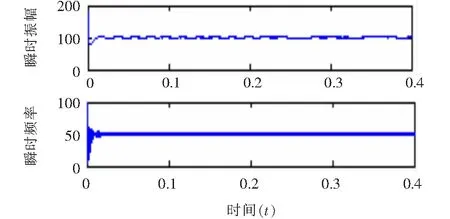
图4 VMD分解基波的Hilbert变换
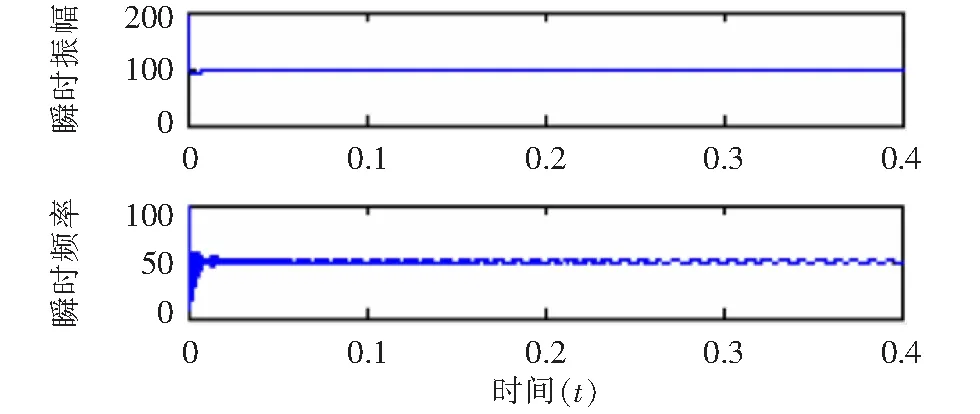
图5 EMD分解基波的Hilbert变换
利用平均值求出以上两种分解方法基波频率和幅值的估计值,在VMD分解下,基波频率的估计值为49.916 3 Hz,幅值的估计值为99.780 5。在EMD分解下,基波频率的估计值为49.923 1 Hz,幅值的估计值为98.764 9。相比之下,两种分解方法对于基波都能准确的分解出来,但是从整体来看VMD分解比EMD分解更能表达原始波形的信息。
3.2 算例2
假设信号x(t)是一个含有谐波的非稳定信号且为:

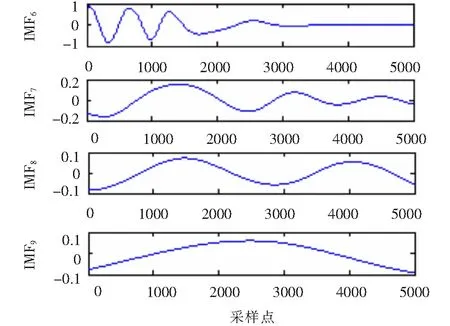
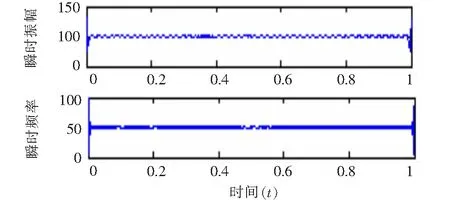
(15)
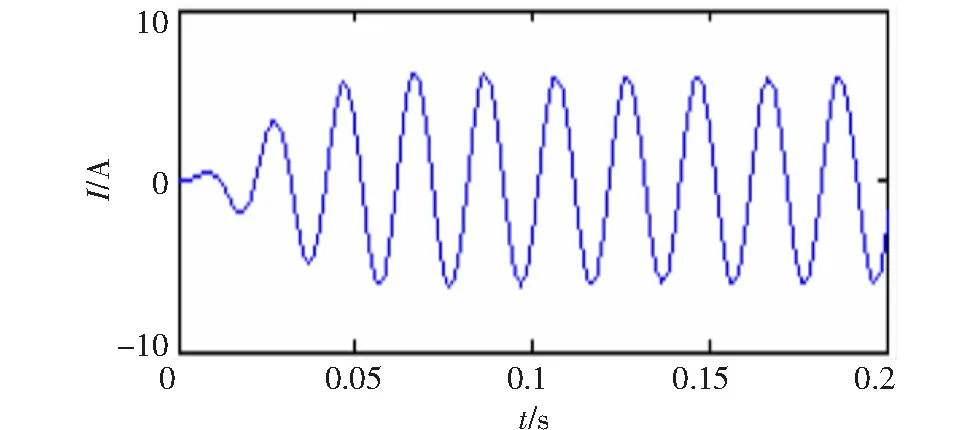
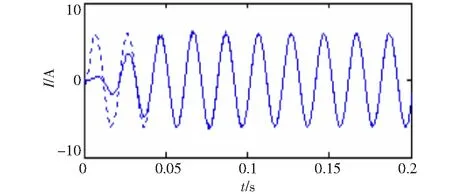
由式(15)可知非稳定信号同样有四中分量,基波信号一直都有,在0.1 s 图6 VMD分解结果 图7 EMD分解结果 由图6可知,IMF1代表了基波分量,IMF2代表250 Hz的谐波分量,IMF3代表150 Hz的谐波分量,IMF4代表350 Hz的谐波分量。VMD分解的结果清晰准确,基本无误差。现在单独分析的基波信号,对IMF1做Hilbert变换结果如图8所示。 图8 VMD分解基波的Hilbert变换 利用平均值得出VMD分解方法基波频率和幅值的估计值分别49.929 8 Hz和99.740 2,所求出的频率误差为0.140 4%,幅值误差为0.259 8%。所以对于VMD分解结果比较准确。而对于图7 EMD分解结果,所分解的第二项为基波,但是在前500点出现了模态混叠现象,使得分解的基波并不完整,失去了原来谐波信号的物理意义。并且EMD分解的结果出现了虚假分量。对于分解结果,显然VMD分解比EMD分解更为精确,更能体现原来谐波信号的信息。 为了更好的说明所提出的VMD分解方法的有效性,谐波源采用比较常见的三相桥式晶闸管的整流电路的实际信号,并且将VMD的检测结果与瞬时无功功率p-q法的检测结果做比较。 图9 a相电流 三相桥式晶闸管的整流电路触发角α=00,电源为三相对称的并且幅值为220 V,频率为50 Hz。采样频率为50 000 Hz,采样点数为20 000个。图9是所给电路中a相负载侧电流ia的波形图。 利用瞬时无功功率p-q法所提取的基波电流ipq如图10所示。 对ia做VMD分解变换,得到的基波电流iV如图11所示。 图10 基波分量ipq 图11 基波分量iV 现在将两种方法所求得的基波分量通过同一坐标下进行比较如图12所示。图中实线为瞬时无功功率p-q法所求得的基波分量,虚线为VMD所求得的基波分量。从图中可看出,当所求得的基波分量稳定后两种发放所得到的基波分量基本一致,并且VMD算法具有更快的收敛时间。 图12 VMD算法与p-q法检测基波分量对比图 为进一步检验VMD方法的检测效果,分别对这两种方法所求得的基波ipq和iV做Hilbert变换,再利用平均值计算出两种方法所检测出的基波的幅值和频率的估计值(为了消除边界效应的影响取中间的数据进行计算)。p-q法所求得结果的估计值为:频率49.993 9 Hz,幅值为6.007 7;VMD法所求得结果的估计值为:频率50.000 3 Hz,幅值5.996 0。通过数据的比较,相对频率来说VMD法比p-q法更为准确。对于幅值,将ipq作为参考量,幅值的平均误差为0.194 8 %。所以对于VMD方法所求得的基波分量无论是从图直观看还是实际数据都表明了是非常准确的。 首次提出基于VMD的谐波检测,通过算例仿真和瞬时无功功率p-q法对比实测数据证明,该方法能准确的检验出电网中的谐波分量。与EMD算法相比,该算法能有效的抑制模态混叠现象,分解出的结果也不含虚假分量,对非稳定信号也能进行准确的分解。VMD算法在进行谐波检测时,无需用到低通滤波器,可很大程度上减少检验误差。本文提出的算法不仅能用在单线电路的谐波检测,也可以用在三相三线制和三相四线制电路中,而且该算法不需要电网电压有无畸变这一条件。并且该算法不仅能检验出谐波,并且能检验出信号中的特定次谐波和间谐波,对分解出的IMF分量做Hilbert变换即可实现,具有很高的推广价值。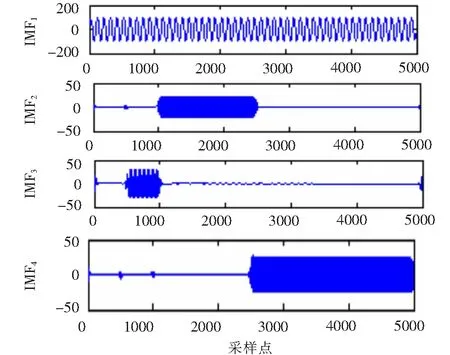

3.3 算例3

4 结束语

