双馈风力发电机故障诊断方法研究*

杨晓光，许仪勋

(上海电力学院 电气工程学院，上海 200090)

0 引 言

目前，中国风机的总装机容量达到了世界风电容量的三分之一，成为世界最大的风电市场。由于风力发电运行状况复杂，发电机组故障率一直处于较高水平，风电机组维护成本较高。对故障设备提早判断，可以在故障早期发现故障，同时进行维修，以避免故障进一步地扩大，从而节省了维护的费用，提高了风电场的经济效益。国内外的统计数据显示，风力发电机组的故障主要发生在叶片、齿轮箱和发电机。

从电机结构来看，可分为定子故障、转子故障、轴承故障等，其中轴承部分故障占40%，定子部分故障为38%，转子部分故障为10%，其他故障占12%[1]。

为了准确的监测双馈风机的故障，国内外学者提出了很多方法，比如将电流信号与振动信号结合起来，通过检测电流信号和振动信号来检测感应电机定子绕组短路故障[2]；对振动信号进行小波滤波，提取与故障有关的早期微弱分量并进行轴承故障诊断[3]。如今，电流频谱分析法可以避免使用振动传感器，电流信号可通过非侵入式监测系统取得，降低了状态监测的成本。

基于快速傅里叶变换(Fast Fourier Transform，FFT)的谐波测量是如今通用的一种高效变换算法[4]，通过采集的电流信号，利用FFT算法进行频域分析，得到电流信号的谐波分量，最后通过判断谐波分量的变化来实现对发电机各种故障的识别。比如，利用定子电流信号的分析和处理来诊断出轴承故障[5]，通过小波技术对双馈感应风力发电机的定子故障进行分析[6]，采用希尔伯特—黄变换提取双馈异步发电机转子电流的故障特征量[7]，通过对比在故障发生前后计算气隙磁场的电磁力的变化，发现转子绕组匝间短路的故障特征[8]。

文章在 MATLAB/Simulink 中建立双馈风机的故障模型，测量双馈异步发电机正常及定、转子绕组匝间短路、轴承故障和混合故障情况下的定、转子电流信号，通过对故障特征频率的理论分析，证实了故障特征量的有效和可靠。分别采用不同的方法进行故障特征量的提取，通过分析和对比，找到监测每个故障所对应的效果最好的窗函数，加rife-vincent窗FFT可以使每种故障判别更加精准、再加上故障特征频率应随风速的变化而调整，可以更好地进行双馈电机的状态监测。

1 DFIG的故障建模与仿真

1.1 双馈式风力发电机的数学模型

1.1.1 电压方程

定、转子侧参数分别由下标s和r表示，定子各相绕组的电阻取值均为rs，转子各相绕组的电阻取值均为rr。

定、转子绕组电压方程分别为：

(1)

(2)

可用矩阵表示为：

式中定子和转子的相电压瞬时值分别是uA、uB、uC、ua、ub、uc，定子和转子的相电流瞬时值分别是iA、iB、iC、ia、ib、ic，各组绕组全磁链为ΨA、ΨB、ΨC、Ψa、Ψb、Ψc，D为微分算子。

1.1.2 磁链方程

各绕组的自感磁链和其他绕组的互感磁链组合成定、转子各绕组的合成磁链，由上边的磁链正方向得到的磁链方程式为:

式中电感是6乘6的矩阵，主对角线上的元素是与下标对应的绕组的自感，非对角线上的元素是下标所对应的两绕组间的互感。

1.1.3 运动方程

由输入的机械转矩和产生的电磁转矩之间的平衡关系来建立交流励磁电机内部的电磁关系。忽略掉转动部件间的摩擦，得到转矩间的平衡关系为：

(5)

式中Tm为原动机的输入机械转矩;Te为电磁转矩;np为电机极对数;J为转动惯量;ω为电角速度。

由机电能量转换的原理得出的电磁转矩方程为：

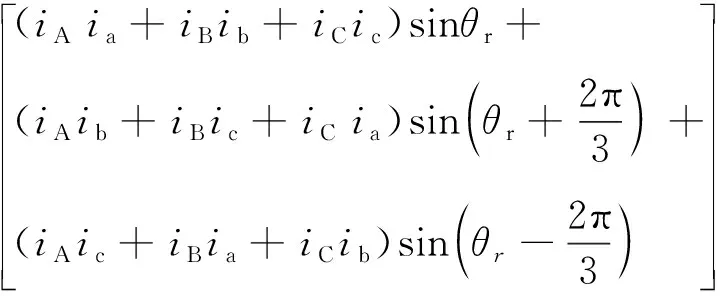
(6)

上述式子组成了在三相静止轴系上的双馈风机数学模型，该数学模型具有非线性、多输入多输出和强耦合等特性，分析和求解比较困难，本文在Simulink中建立双馈风机的模型。

1.2 双馈式风力发电机的故障建模

含双馈风机的电力系统Simulink模型如图 1 所示。此系统模拟了一个9 MW的风电场，其包括了6个1.5 MW的双馈风力发电机，与一个向120 kV电网供电的25 kV的配电系统，通过30 km、25 kV的馈电线连接。由绕线转子异步发电机和基于IGBT的交流/直流/交流电压源型PWM转换器组成了该双馈风力发电机。电网的频率为60 Hz，定子绕组直接连接到电网，而转子则由AC/DC/AC转换器反馈到电网。

图1 含双馈风机的电力系统模型

2 故障分析

2.1 故障谐波分析

DFIG的绕组一般采用三相对称的绕组，相绕组通电时，由于组成绕组的各个线圈磁通势波形中分数次和低次的谐波会相互抵消，所以相绕组总磁通势的波形主要是基波。当定、转子绕组发生匝间短路时，将在定、转子电流中感应出相应的谐波分量。

单匝线圈磁动势的傅里叶级数展开式为：

(7)

式中α为空间电角度;P为极对数;kyv为单匝线圈节距因数;ω为电流角速度；v为谐波次数，对于短距线圈v=1/P,2/P,…,对于整距线圈v≠2,4,6,…。

假设发生定、转子绕组短路后，会在短路匝上叠加电流，1和2分别代表定、转子，叠加电流为：

(8)

短路匝沿气隙圆周的空间电角度α分别为Pθ和Pφ。则在定、转子短路匝线圈磁动势分解后，傅里叶级数的展开式分别如下:

(9)

(10)

式中ω1、ω2分别为定、转子电流角速度;θ、φ分别为定、转子坐标表示的机械角度;θ=φ+[(1-s)ω1t]/P;ω2=sω1;s为转差率。

定子绕组发生匝间短路故障时，在转子坐标系中，f(θ,t)的表达式可以表示为：

(11)

在转子线圈中，磁动势f(φd,t)感应出的电势为：

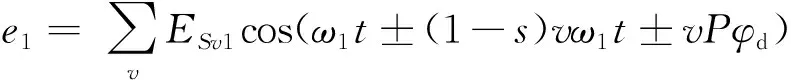
(12)

式中ESv1为转子侧的线圈感应电动势v次谐波的有效值。当发生定子绕组匝间短路故障时，转子侧线圈的感应电流中所包含的谐波分量为[1±v(1-s)]f1；当以θ取代式(12)中的φd，可得到f(θ,t)在定子侧线圈的感应电流中所包含的谐波分量为[1+(n±v)(1-s)]f1，其中，f1为定子侧电流频率[9]，n=6k±1,k=0,1,2,…。

当发生转子绕组匝间短路故障时，f(φ,t)在定子坐标系中的表达式可以表示为：

(13)

在定子线圈中，磁动势f(θz,t)感应的电势为：

(14)

式中ESv2为定子侧的线圈感应电动势的v次谐波有效值。转子绕组发生匝间短路故障时，定子侧线圈中感应电流所包含的谐波分量为[1 ±v(1-s)/s]f2，其中f2为转子侧电流频率[10]。

当轴承发生故障时会引起电机转轴振动，转轴的振动会引起电动机内膛气隙振动，气隙磁通将会受到调制，在定子绕组中感应出特定的谐波电流，所以，可以通过对定子电流波形的分析，来提取出与振动水平相对应的谐波分量，从而检测出轴承故障。大部分的电动机轴承振动频率可用下式来表示：

fi=0.4nfz；fo=0.6nfz

(15)

式中fi和fo分别为轴承内、外圈故障时的振动特征频率;n为轴承滚珠的数目;fz为转子频率。通过振动特征频率可算出定子电流中相应故障特征频率为|f3±kfbug|，式中k=1,2,3,…，f3为风机的供电频率，fbug为转矩的振动频率[11]。

2.2 故障波形分析

利用图1中模型，分别对电机正常运行情况，定、转子匝间短路，轴承故障，定、转子绕组匝间短路故障和轴承故障的混合故障6种情况进行仿真，设置A相为故障相，得到6种情况下的定、转子三相电流。电机正常运行和定子匝间短路故障情况下的定子三相电流波形的稳态时刻如2图所示，转子绕组匝间短路和轴承故障情况下的定子三相电流波形的稳态时刻如图3所示，四种情况下转子三相电流如图4所示，定、转子绕组匝间短路故障和轴承故障的混合故障的定子三相电流如图5所示。

如图2～图5所示，当双馈式电机正常运行时，定、转子侧三相电流的大小相等，相位差为120°，波形较为平滑，虽有些轻微波动，但不是很明显，基本上没有其他频次的谐波。定子故障时，定子三相电流产生了轻微不对称的现象，幅值与正常情况相比均有不同程度的提升；转子三相电流和正常情况相比有了较为明显的波动，但三相电流基本保持对称关系不变；所以，定、转子侧的电流中都含有谐波成分。转子故障时，定子三相电流发生畸变，三相电流幅值均有一定程度的波动；转子三相电流发生不对称现象，故障相A相电流最大。轴承故障时，定、转子三相电流的幅值与正常情况相比都略有减小；发生混合故障时，不同的混合故障下定子三相电流幅值与正常情况下相比既有增大又有减小，且存在一定程度的相角差。由上述结果可以看出，该仿真实验的结果符合DFIG的设计原理。

图2 正常情况和定子故障时定子三相电流

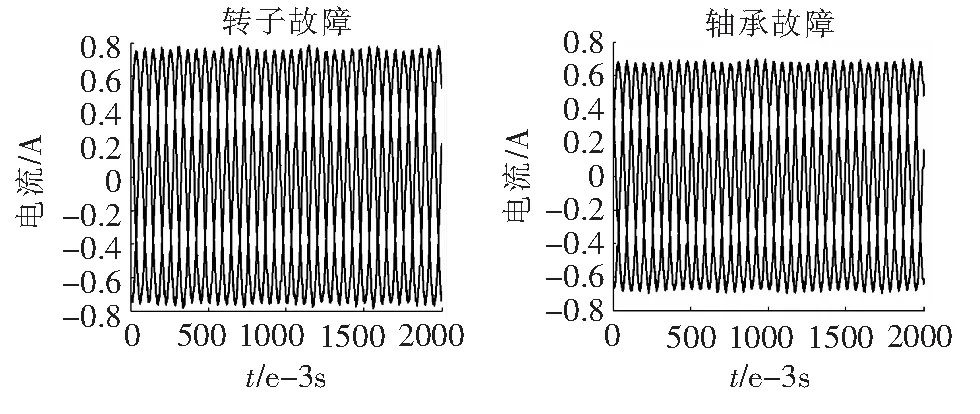
图3 转子故障和轴承故障时定子三相电流

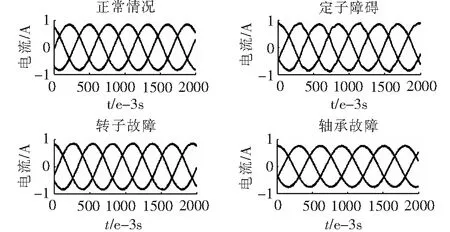
图4 四种情况下转子三相电流

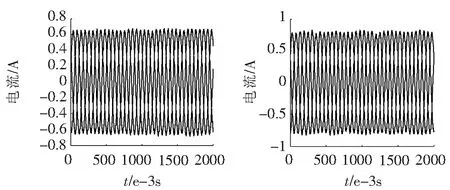
图5 定转子与轴承混合故障定子三相电流

3 仿真实验分析

3.1 故障特征量的提取

3.1.1 Zoom FFT 复调制方法

频谱细化分析采用的是高分辨率的傅里叶分析方法，在信号频谱中需要研究的一处频段增大其谱线的密度，从而准确地分析出故障特征频率的成分。复调制细化谱分析方法的计算流程如图6所示。

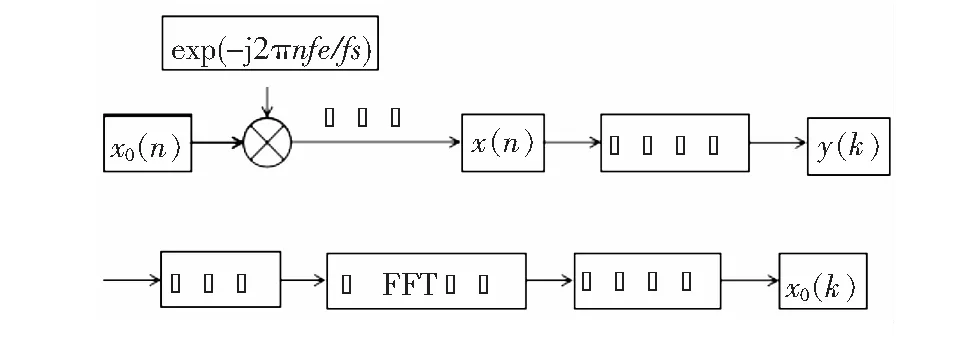
图6 基于复调制的ZoomFFT算法流程图

对离散信号x0(n)以exp(-j2πnfe/fs)进行复调制，得到移频信号x(n)，通过低通滤波、重采样、复FFT处理、频率调整等步骤得到细化后的信号x0(k)，fe为欲观测频带的中心频率，fs为采样频率，此时的Δf=fs/ND，D为细化倍数。ZoomFFT虽然提高了频率分辨率从而使结果更加准确，但是其运算量大、处理速度低、占用资源大，并且其较高的分辨率只能在某一较小的频率范围内进行频谱分析，所以不适用于进行大范围的频谱分析[11]。

对故障信号分区域进行ZoomFFT变换处理，得到了较为精确的故障特征量及此处的幅值大小，如表1所示。图7为频率细化分析范围为82 Hz～86 Hz时的细化频谱图，此时Δf=0.1，频率84 Hz处的幅值比较准确。

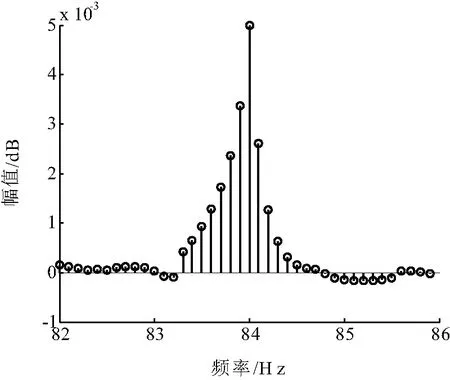
图7 ZoomFFT后的细化频谱图

3.1.2 加窗傅里叶变换方法

FFT作为一种经典的谐波检测方法，高性能窗函数可以有效地消除频谱泄露和栅栏效应，从而提高了谐波参数的检测精度。在FFT添加triang窗，hanning窗，hamming窗，chebwin窗，kaiser窗，blackman窗，rife-vincent窗对谐波进行检测。当不知要用哪一种窗函数对信号进行处理时，应该多试用几种窗函数，通过比较加入这几种窗函数后的检测效果，来决定使用哪种窗函数更加符合实际情况。为了确定哪种窗函数对检测双馈风机故障特征更加有效，对定、转子和轴承故障的定子电流进行频谱分析。如表1所示，选择7种窗函数分别对故障情况时的定子电流进行加窗FFT变换。在正常情况下，定子电流中主要含有基波60 Hz，还会含有少量的奇数次谐波。

由表1可以看出，在定、转子绕组发生匝间短路故障时，在定子电流中会含有12 Hz,36 Hz,84 Hz,108 Hz,132 Hz,156 Hz等频率的谐波，轴承故障时，20 Hz,100 Hz,140 Hz,180 Hz,220 Hz等频率的谐波会出现在定子电流中，这与第二节理论分析的故障特征频率相符合。

根据实验验证，当发生定子绕组匝间短路故障时，定子侧三相电流不再互成120°，存在三相相角差，两两之间的相角差分别为122.6°、117.8°和116.5°；当发生转子绕组匝间短路故障时，定子侧三相电流保持对称都为120°。定、转子绕组匝间短路故障后，定子侧故障特征频率相同，可依据定子侧三相电流的相角差来区分定转子绕组匝间短路故障。

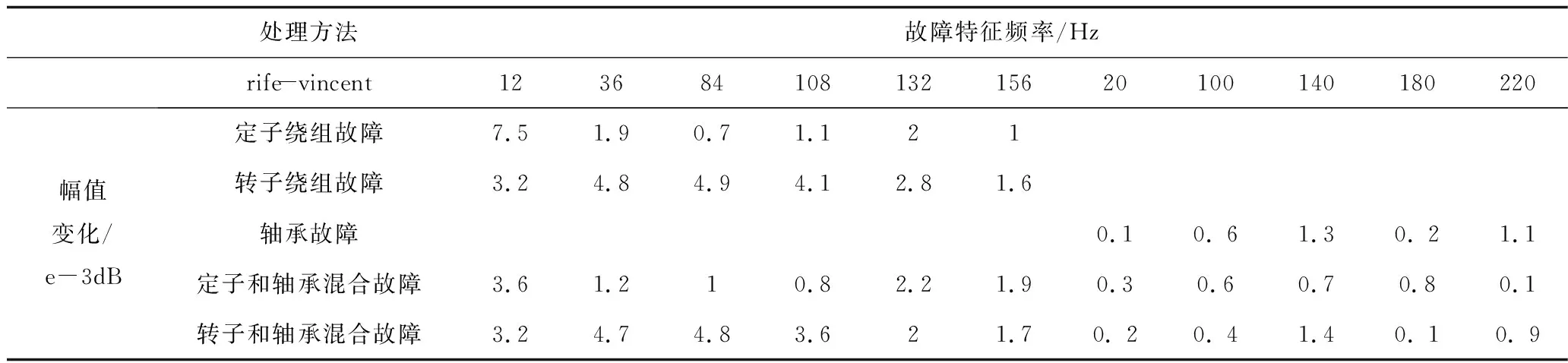
表1 各种处理方法效果比较

对选择的所有处理方法的效果进行比较，如表1所示，在定转子绕组故障和轴承故障前后，均是加入rife-vincent窗后幅值变化最大，与进行ZoomFFT变换后的幅值变化大小相接近，故在处理双馈风机定、转子绕组匝间短路故障和轴承故障时，加入rife-vincent窗比加入其他窗函数进行FFT变换的幅值变化更明显，更加有效的反映出了故障特征频率，提高了可靠性。图8和图9分别为在转子绕组匝间故障时，加rife-vincent窗和kaiser窗后的定子电流频谱图，由图中看出，加rife-vincent窗后的故障频率所受干扰较小，且其它频率的幅值较小，故障频率可分辨性更强。与其他窗函数相比，rife-vincent窗的抗干扰性和可分辨性均优于其他窗函数，由于ZoomFFT不适用于进行大范围的频谱分析，所以，加rife-vincent窗FFT比较适合双馈风机定、转子绕组故障和轴承故障的谐波分析和处理。

当双馈风机发生混合故障时，对三种单一故障和两种混合故障的定子电流分别进行处理，使用表1所示的方法，实验验证使用加rife-vincent窗FFT比其他方法所得到的幅值变化率更大，处理混合故障数据可分辨性更强。表2为使用加rife-vincent窗FFT对单一故障和混合故障的定子电流进行频谱分析得到的幅值变化情况，混合故障的故障特征频率处幅值的大小并不是单一故障的故障特征频率处幅值的简单叠加，而是一组新的幅值变化情况，所以对于混合故障同样需要进行处理方法的匹配来找到更加可靠的处理方法。

对于双馈风机的定、转子绕组匝间短路故障，轴承故障，定、转子绕组匝间短路故障和轴承故障的混合故障这五种故障来说，使用加rife-vincent窗FFT进行故障数据的处理和分析具有良好的可靠性、灵敏性和可分辨性。

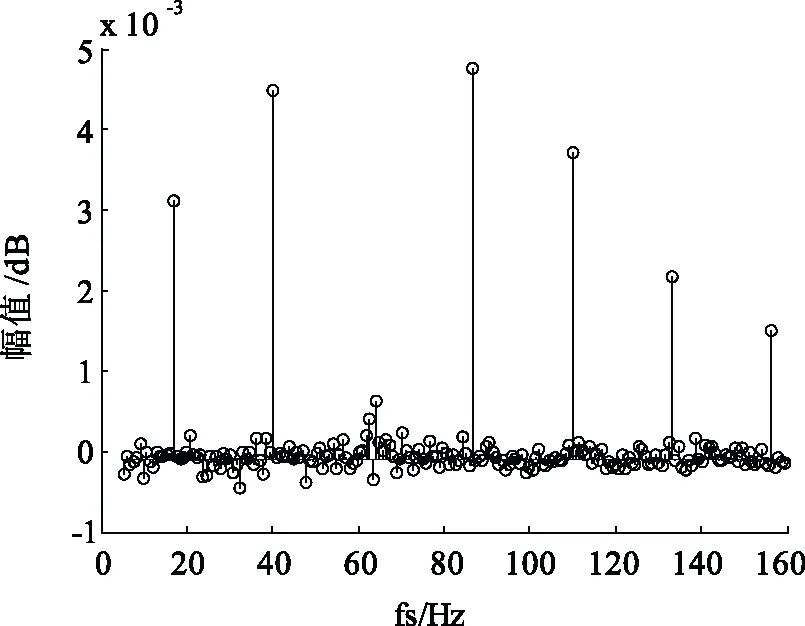
图8 转子绕组匝间故障时，加rife-vincent窗的频谱图

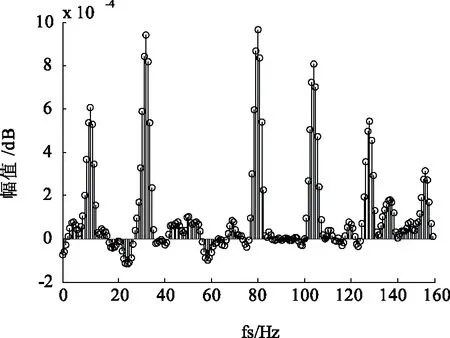
图9 转子绕组匝间故障时，加kaiser窗的频谱图

处理方法故障特征频率/Hzrife-vincent12368410813215620100140180220幅值变化/e-3dB定子绕组故障7.51.90.71.121转子绕组故障3.24.84.94.12.81.6轴承故障0.10. 61.30. 21.1定子和轴承混合故障3.61.210.82.21.90.30.60.70.80.1转子和轴承混合故障3.24.74.83.621.70. 20. 41.40. 10. 9

3.2风速对故障特征频率的影响

双馈风机故障模型的额定风速为15 m/s，改变风速后，通过加rife-vincent窗FFT进行故障特征频率的分析，发现故障特征频率处的幅值均有不同程度的变小，如表3所示。随着实际风速与额定风速之间差值的变大，故障特征频率的幅值越来越小，使得故障检测结果不明显，风速的变化会削弱对故障特征频率的判断。所以在风速变化较大时，应根据实际风速情况来调整故障参考值，以便对双馈风机的故障做出更加准确的判断

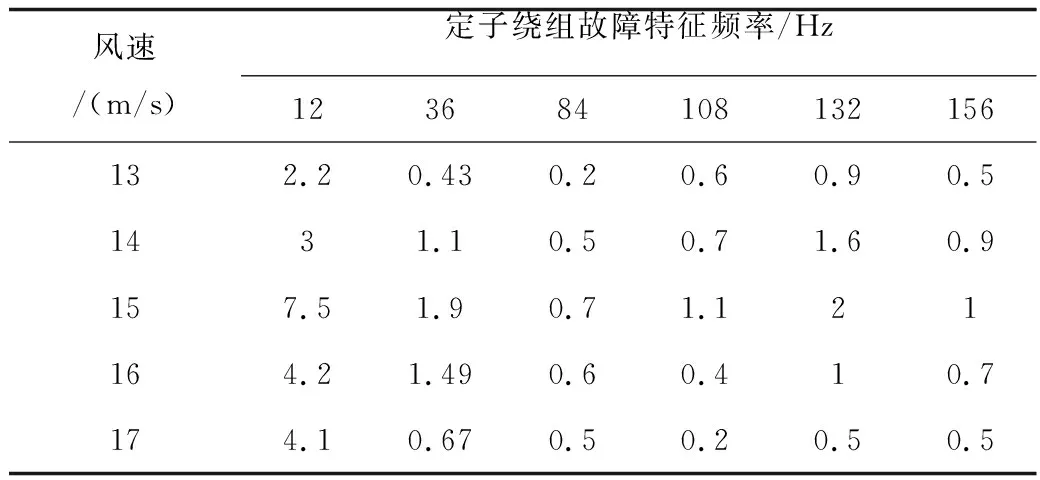
表3 风速变化时故障特征频率幅值的变化

4 结束语

在 MATLAB/Simulink 中建立了双馈风机的电力系统故障仿真模型，通过设置不同的故障得到了双馈异步发电机正常，定、转子绕组匝间短路故障，轴承故障和混合故障情况下的定、转子电流信号及图像，并提取了故障特征频率。并对不同的故障特征进行理论分析得出故障特征频率，通过与故障模型所得出的故障特征频率的对比验证了DFIG故障模型的正确性。采用ZoomFFT和多种加窗傅里叶变换进行故障特征量的提取，ZoomFFT精度最高但分析应用范围太小，通过与ZoomFFT方法进行频谱分析并对比，得出加rife-vincent窗FFT在处理双馈风机故障时幅值大小与ZoomFFT方法相接近，具有较好的抗干扰性、可分辨性与可靠性，而且可用于整个故障的分析。风速的变化会削弱对故障特征频率的判断，应根据实际风速的变化来调整故障参考值。这样可使得每种故障判别更加精准、监测更加有效，减少发生故障误判的可能性，从而达到更好的双馈电机状态监测效果。