重大件货物立式运输系固设计

刘向冬 丁 超

（上海船舶研究设计院，上海 201203）

0 前言

随着生产工艺和建造技术的不断提高，建筑、桥梁建设、机械制造等行业的设备或结构物日趋大型化。此类重大件结构物由生产车间完成组装，然后通过一定方式运送到施工现场投入使用。这样减少了现场组装零件的繁琐工序，提高了现场建造效率，然而被运输货物的大型化发展对系固、绑扎和运输提出了更高的要求。相比于陆上运输，水路运输不仅对重大件货物的重量、尺寸限制较少，而且安全经济［1］。近年来，重大件货物在船舶杂货运输中所占的比重日益增多，与此同时由于货物系固不良引起的船舶事故也呈增长趋势。因此，对重大件货物的系固安全进行研究具有重要价值。

1 重大件货物系固

1.1 概念

重大件货物一般指体积过大或尺度过长的货物。它以货物单件重量及尺度作为界限，国际航运中凡单件重量超过5 t或者单件长度超过9 m的货物，沿海运输中凡单件重量超过3 t或者单件长度超过 12 m 的货物，均属于重大件货物［2－3］。大高宽比的重大件货物系指结构重量大且高度和宽度比值较大的结构物。例如安徽某长江大桥钢桁梁，由于现场施工的需要，采用立式运输由生产地运往建设现场进行架设，单件重达350 t，尺寸为30 m×18 m×2.84 m，高度与宽度比值达6.3，如图1所示。

图1 某长江大桥钢桁梁其中某段主桁片

重大件货物属于非标准货物，由于其体积大，自重大等结构特点，很多情况下无法在陆上运输，只能采取水上运输的方式。通常需用特殊系固索具对货物进行绑扎、固定，使其在运输的过程中不会因为船舶的运动而发生滑移或倾倒［4］，而影响货物及船舶的安全。

1.2 系固方式及系固设备

重大件货物的系固主要分为柔性系固和刚性系固两种方法。柔性系固采用绳索、铁链、钢丝和其他的紧固索具将货物固定于船舶的货舱或者承重甲板之上；刚性系固是将货物固定在专门设计的支座上，然后将货物和支座一起固定于船舶的货舱或者其他承重部位，通常是将支座、货物与船体焊接在一起，与船联结成一个整体［5］。

2 外力的计算方法

2.1 外力的来源分析

在选择合适的系固方案之前须要知道外力是如何产生的。对载有重大件货物的船舶，其在运动过程中由于风浪的作用会产生6个自由度的运动，其中横摇、横荡对系固货物的绑索载荷影响最大，垂荡及纵摇的影响次之，首摇及纵荡的影响可以忽略［6］。如果将船舶的运动简化为简谐运动的合成，那么船舶运动主要包括横摇、横荡、垂荡和纵摇四个独立的简谐运动。横摇产生横摇角加速度，横荡产生横向水平加速度，垂荡产生垂直方向加速度，纵摇产生纵摇角加速度。这一系列加速度产生的惯性力最终作用在重大件上。因此，系固的目的是平衡这些惯性力，将重大件牢牢地固定在船体上，使其不会因为惯性力的作用而与船体发生相对运动。

2.2 惯性加速度

已知惯性力由加速度产生，因此，在确定力的大小之前必须求得运动过程中各加速度的大小［7］。

2.2.1 船舶横摇角加速度

根据运输船舶装载货物时的稳性资料，可得知其装载状态下的稳性高GM，从而可得到该船装载此货物在某航区航行时的横摇周期及角度等参数。

再根据横摇角加速度公式求得船舶运动的横摇角加速度大小，见式（1）：

式中：φ——最大横摇角，（°）；

Tφ——横摇周期，s

2.2.2 船舶横荡加速度

船舶航行于水面上不仅会产生横摇，也会产生横向回荡的运动从而产生横荡加速度。这也是货物横向外力产生的原因之一。

由式（2）即可求得横荡加速度αd：

式中：S——航行系数，应按航区选取：

C——系数，应按式（3）计算：

L——船长，m；

Cv=/50，取不大于0.2；v——最大服务航速，kn

由此得到航行中船舶横荡产生的加速度。至此，船舶在航行过程中的横向加速度均已求得。这两个加速度也是货物产生横向力的主要因素。

2.2.3 船舶垂荡及纵摇的加速度

垂荡加速度αZ应按式（4）计算：

式中：Cb——方形系数

纵摇角加速度ψ″应按式（5）计算：

式中：ψ——最大纵摇角，（°）；

Tψ——纵摇周期，s

2.2.4 货物加速度

前面已求出船舶运动时的加速度，然而，这些加速度还需进一步由船体转移到计算的货物上，如图2所示。

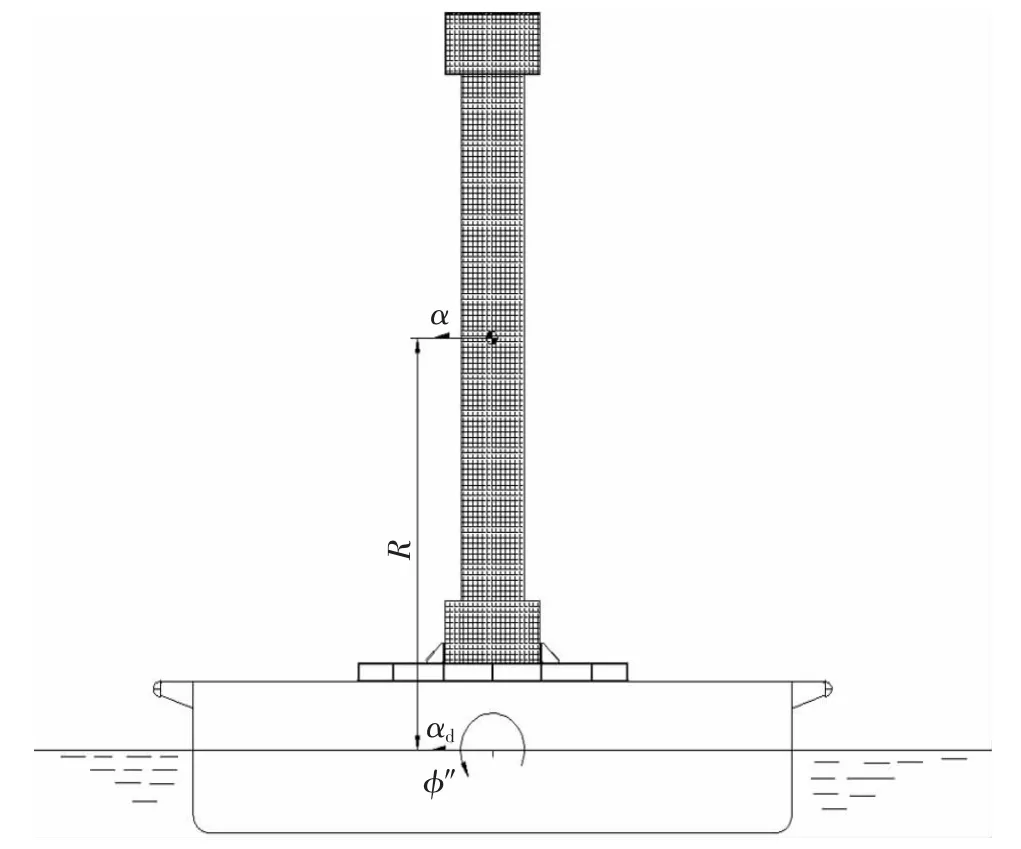
图2 船体及货物加速度关系图

假设运载的货物为刚体，那么加速度则作用在其中心位置，货物的重心距旋转中心（船舶的漂心）的距离为R，货物相对船体静止，即具有和船体一样的加速度。为了得到货物在重心处的惯性力大小，需要将角加速度转化为线加速度，则横摇在货物上产生的线加速度大小为Rφ″。

货物上的合加速度a由横摇线加速度和横荡加速度两部分组成。因此，相应的惯性力也可由经典力学公式F=ma求得。

船舶和货物所受到的风力可根据相应法规求得，在此不作赘述。

3 货物系固中系固力的计算

本文主要研究用甲板船运输大高宽比的重大件，其布置形式如图2所示。在实际工作中，重大件货物的运输并不少见，如钢箱梁结构的桥梁分段、港珠澳大桥海底隧道的分段以及海洋风机的叶片等，均具有较大的底面积。对于本文中重大件，不仅要防止其在甲板上的滑动，更要防止其倾倒，因此要求系固点在产生水平力的同时还要能产生足够大的力矩使货物稳固。在此不宜采用斜撑等刚性固定，因为支撑构件过长易发生失稳，所以经过研究决定对于此类货物采用柔性系固较佳。

甲板系固点与大件系固点的连接形式，如图3所示。

分别在驳船甲板的左舷及右舷设置一定数量的绑扎眼板，同时重大件货物上也设置对应数量的绑扎眼板，采用钢索连接进行系固绑扎。

系固用的钢索产生拉力，将惯性力抵消，从而使重大件能够与船体保持一个整体。因此，钢索上所能承受的最大拉力须满足最危险的情况，才能保证系固设备不被破坏。

对于简谐运动，当速度最大时，加速度最小，反之，当速度减小到零时，加速度达到最大。因此，当达到最大横摇角时，船体受到最大回复力矩，有最大的横摇加速度；横荡运动亦是如此，当达到最大横荡位移时，速度为零，而加速度达到最大。因此，将这两种简谐运动合成，就得到最危险的时刻即当横摇和横荡均达到最大值的时候。此时，整个系统的受力如图4所示。

图4 系统受力图

由于是柔性系固，钢索只能产生拉力，因此只有一边的钢索对货物产生拉力。通过力学分析可知，钢索拉力、货物惯性力、风力及摩擦力达到平衡，有如下平衡方程式。

沿甲板宽度方向力的平衡方程见式（6）：

绕旋转点矩的平衡方程见式（7）：

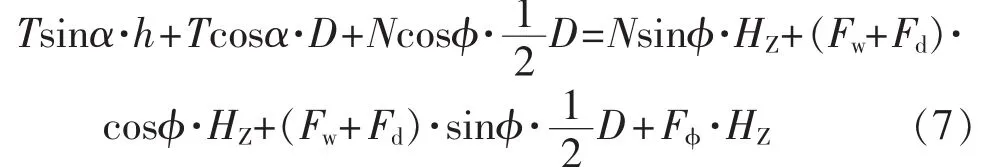
式中：T——绳索的拉力，kN；

α——绳索与桁片的夹角，（°）；

Ff——桁片底端的摩擦力，kN；

Fd——横荡惯性力，kN；

φ——最大横摇角，（°）；

Fw——桁片受到的风倾力，kN；

Fφ——横摇惯性力，kN；

N——垂向惯性力，kN；

h——桁片上的系固点距甲板的垂直距离，m；D——桁片的宽度，m；

HZ——桁片的重心距甲板的距离，m

对式（6）进行变形得到：

不难看出，针对某一实际情况分子中各项均为定值，因此，对T的大小真正有影响的是分母。式中α 有式（9）关系式：

式中：d——船上系固点到桁片边缘的距离，m

因此，若系固点选择得当，则可降低绳上的拉力。

式中有两个变量h和d，无法直接解得，可采用控制变量法通过绘制曲线加以分析，具体如下：

首先确定d，选择不同的h进行一组计算，从而得出在该d的情况下，拉力T随h的变化曲线，然后，用相同方法分别计算 d为 2 m、4 m、6 m、8 m、10 m的情况，h值从1 m至30 m每一米计算一次，计算结果如图5所示。

图5 绳索所受拉力与系固点的位置关系图

图 5中绘出了 d分别为 2 m、4 m、6 m、8 m、10 m时的T随h的变化情况。可以清晰地看出，对于同一货物，船上的系固点位置决定了系固力的最小值，即当船上的系固点距桁片越远时，系固力的最小值越小；当d一定时，T会随h的增大而减小，并最终趋近于一个定值。故船体上系固点离货物越远越有利，同时，在船体系固点已经确定的情况下，货物上的系固点越高越有利。

进一步分析可知，虽然d的增大降低了系固力的最小值，然而降低的幅度是在减小的，特别是当d的值超过一定范围以后，通过继续增加d来进一步降低系固力的最小值的作用就变得非常有限了；对于某一确定的d而言，虽然起初T随h的增加而迅速减小，然而当h超过某个临界值以后，曲线下降的就极为缓慢了，继续增大h对系固力的降低作用不大。这两种情况下，继续增大d和h对减小系固力作用不大，然而却使钢索长度迅速增加。由于钢索自身存在重力，会使得钢索存在下垂的现象，越长的钢索就越难保证系固的拉直度，对紧固是极为不利的，而且不必要的增长钢索也造成了材料的浪费，加大了项目的开支以及运输成本。这在实际操作中都是应当避免的。

得到绳索拉力T之后，将其代入式（6）中求出摩擦力。若摩擦力的值低于临界摩擦力，则满足要求；若摩擦力大于临界摩擦力，则应当在底端设置一定的防滑移设备，以防止重大件在甲板上发生横向滑动造成危险。

4 系固实例

4.1 工程概况

安徽某长江大桥连续钢桁梁共22个桁段，分为66件即每个桁段包括一个主桁片和两个边桁片。该重大件的运输共分为22次，每次运输一个桁段。本文选取其中一个桁段的主桁片作为实例进行系固计算。该桁段主桁片长30 m，高18 m，宽2.85 m，重为265.994 t。

运输船舶为甲板驳船，垂线间长72.5 m，型宽18 m，型深4 m，航区为内河A级。

4.2 货物综合外力的计算

主桁片布置于船中，系固情况如图3所示。由船舶相关稳性资料可知，最大横摇角φ为0.096°，最大纵摇角ψ为0.03°，横摇周期Tφ为7.45 s，纵摇周期Tψ为 6.28 s，垂荡周期 TZ为 3.49 s。

根据第二章公式计算惯性加速度，并最终求得惯性力 Fφ=164.4 kN，Fd=325.4 kN，N=3 441 kN，Fψ=72.3 kN，同时还根据法规求得横向受风力Fw=70.395 kN。由此可以看出，桁片受到的横向惯性力远大于纵向惯性力，因此横向系固是最主要的考虑内容。

4.3 系索系固布置及系索拉力计算

由第三章已经得知，拉力计算式（8）中分子是定值，因此，可先求得其值为4 149.09（此处计算时会发现，最大值发生在船舶垂荡至最高点，同时有最大横摇角及最大横荡位移的时刻）。该船最大型宽为18 m，主桁片布置于船中，因船体上系固点距货物越远越有利，故将系固点选取在舷边强构件交汇处，则d=9－0.5×2.84=7.58 m，采用第三章作图法，可得到该算例情况下的T-h曲线，如图6～图8所示。

图6 每舷4根钢索时，绳索所受拉力与系固点的位置关系图

图7 每舷6根钢索时，绳索所受拉力与系固点的位置关系图

图8 每舷8根钢索时，绳索所受拉力与系固点的位置关系图

图6 ～图8中，钢丝均按照捆绑要求取安全系数为8（用于捆绑的钢索安全系数一般取8～10）。图6中每舷4根钢索，最低能够满足系固强度要求的是直径28 mm的钢索，只要桁片上的系固点高度超过10.5 m即可。图7中每舷6根钢丝，最低直径21.5 mm的钢索可以满足要求，此时系固点高于17.1 m即可；图8中每舷8根钢索，只需要直径19.5 mm的钢丝即可，系固点应当高于12.1 m。

根据以上数据，即可依照自身的能力选配适当数量及型号的索具。至此，已经确定了d及h的具体位置，从而可以得到拉力T的具体值，将其代入式（6）中检验摩擦力是否小于临界摩擦力。若小于，则满足要求；若大于，则需要在货物底端增设适当的横向限位装置，以防止其滑动。

5 结语

本论文主要针对重大件货物系固的相关问题进行探讨，通过计算运输过程中货物所受到的外力，对系固索具进行受力分析，从而确定系固方案。本文的结论如下：

1）船体上系固点离货物越远越有利，同时，在船体系固点已经确定的情况下，货物上的系固点越高越有利。

2）随着船体上系固点的远离，虽然绳索上能够达到的最小系固力在逐渐减小，然而减小幅度是在降低的，因此没有必要无限制地选取较远点。同样，货物上系固点的升高有利于绳索接近最小系固力，然而达到某一高度后，系固力降低的就不太明显了，因此应根据实际情况进行合理选取。这样对系索拉紧和节省材料都是有利的。

本文的研究工作旨在为重大件货物的安全、高效运输提供一定的参考和帮助。