阻尼对振动筛振动系统的影响性分析

白 龙，赵星檑

(神华神东煤炭集团公司洗选中心，陕西 神木 719315)

0 引言

振动筛作为选煤厂的主要设备之一，用于原煤的筛分、商品煤的脱水筛分以及洗选过程中的脱泥脱水作业，根据振动形式分为圆振动筛和直线振动筛，受到筛分效率、处理能力、振动强度、使用寿命等因素的影响，直线振动筛的数量明显多于圆振动筛。直线振动筛主要依靠2个激振装置同步反向旋转使激振器在振动方向上产生反向交替的激振力，而垂直振动方向则相互抵消，迫使筛体箱带动筛板做直线振动，使筛上的物料受激振力而周期性地向前抛出一个射程，从而完成物料筛分作业[1]。

1 振动筛的理论研究

振动筛理论研究采用有限元分析的方法对其进行静力学分析、模态分析和谐响应分析，从而为改进筛机结构、确定传感器的安装位置、确定金属磁记忆检查范围以及设定故障报警阈值提供理论依据[2-4]。

首先获取振动筛的各项数据，根据数据用Solidworks进行三维建模，将模型导入有限元分析软件，然后将整个筛机划分成多个网格，对参数进行定义(即添加各种材料属性)，设定约束边界的工作；在此基础上，对振动筛分别进行静力学特征和模态特征分析，得到振动筛的应力应变情况，固有频率和振型；最后添加激振力和激振频率，对振动筛进行谐响应分析和疲劳应力分析，得到工作频率下整机和关注部位的位移情况，便于在线监测[5]。

1.1 振动筛三维建模

根据现场测试的数据再结合申克厂家提供的有限图纸，用solidworks对振动筛的所有零部件进行了建模，小到螺母、大到筛体，在此基础上构建了振动筛整体模型，在有限元分析过程中，复杂的模型分析要以高的计算机配置和时间为代价，细小的零部件对整机工作状态的影响可以忽略，故对模型进行适当的简化处理[6]。

1.2 模型导入

通过Workbench与SolidWorks的相应接口将三维模型导入到Ansys有限元分析软件，建立有限元模型。

将Solidworks建立好的振动筛的三维仿真模型导入Workbench，其常用的方法主要有2种：一种是通过Workbench识别igs格式，需要将Solidworks建立好的振动筛的三维仿真模型另存为igs的格式，然后导入到DS中进行使用。另一种是在Solidworks本身自带的系统菜单栏有Workbench的接口按钮，通过鼠标单击的方式可进入Workbench界面。

Solidworks是一款能够为用户提供一系列三维设计产品，可以极大地帮助设计师节约设计所需要的时间，同时还能够提高设计的精确性和创新性的软件。具有易学易用、技术创新和功能强大3大特点。

ANSYSANSYS软件是一种大型通用有限元分析软件，它将结构、电场、流体、磁场、声场分析融合在一起。该软件作为现代产品设计中的高级CAE工具，能够与大多数的CAD软件进行完美对接，能够实现数据的交换与共享，具有良好的实用性[7]。

软件主要由3部分组成，分别是前处理模块、分析计算模块、后处理模块[7]。①前处理模块主要作用是对实体进行网格划分，并根据划分的网格的数据进行实体建模，方便用户构造有限元模型；②分析计算模块主要包括结构分析、声场分析、电磁场分析、流体动力学分析、压电分析以及多物理场的耦合分析，其中结构分析包括可进行非线性分析、高度非线性分析和线性分析，通过上述各种分析功能，使得该模块具有优化分析及较高灵敏度分析的能力，同时还可以实现不同的物理介质的相互作用的实体模拟；③后处理模块的主要功能是将计算得到的结果采用不同的模式显示出来，显示模式主要有彩色等值线显示、梯度显示、粒子流迹显示、矢量显示、半透明显示及透明(可看到结构内部)和立体切片显示，也可通过曲线、图表等形式将计算结果显示出来或输出。

1.3 添加材料属性

部件定义：在对振动筛进行模态分析之前，为了使分析更加细化明确，要将整个筛机的各个部件分别进行定义。①根据筛机各结构部件采用的材料，通过查阅机械设计手册获得金属材料属性；②实际测量弹簧的各个参数从而获得其弹簧外径、簧丝直径、弹簧中径、弹簧内径、自由高度、节距、总圈数、有效圈数，并通过万能试验机获取弹簧刚度。

弹簧刚度试验：对弹簧进行静刚度测试，采用的测试工具主要包括游标卡尺、卷尺以及万能试验机。测试对象是申克SLO3673型振动筛的一个新弹簧和一个坏弹簧，通过相关计算得，新弹簧的静刚度为：K=308.11 N/mm，坏弹簧的静刚度为：K=202.35 N/mm。通过测试可知，前一种新弹簧由于加载面完好，受力比较均匀，弹簧整体在压缩过程中未发生明显的弯曲，所以通过测量计算出的静刚度可信度比较高；后一种坏弹簧，虽然对其断面进行了打磨处理，但在加载过程中弹簧整体发生明显的弯曲，则所测量计算出的静刚度不可靠。

1.4 网格划分

有限元网格的划分直接影响到整个计算结果的准确度，网格划的太密对于提高计算精度的作用不是很明显，同时又会增加大量的计算，太疏影响计算精度。因此，要合理地网格划分。本论文中采用自由划分和扫略2种方式相结合的方法对整个模型进行网格划分，设置零件间默认检测固联距离为7.4 mm，联接允许值50。单元最小边长度为2.453 0 mm，取网格细化参数为10，总共划分成506 217个单元、包括1 034 349个节点，如图1所示。

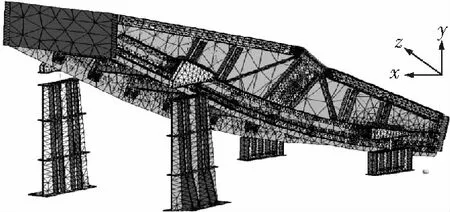
图1 CAE分析网格划分

1.5 施加约束边界

振动筛板筋和筛箱的连接均采用固连，支架固定在地面，通过4组实体弹簧(每组3个弹簧)与整个箱体连接。

1.6 静力学分析

振动筛在长期使用过程中应力集中后的疲劳破坏经常会导致结构破坏。因此，需要找出振动筛主要部件和整体的应力集中位置。

通过对整个筛箱进行静力学分析得到的各主要部件的应力分布情况，见表1。

表1 应力分布统计表

1.7 模态分析

振动筛的模态分析，为整个在线监测系统提供了主要的模态参数，为改进和提高振动筛的性能提供了强有力的理论支持，同时为进一步的结构优化、筛机疲劳寿命预测和振动动力学分析做好准备。

通过ANSYS Workbench对整个筛机的振动进行模态分析得到以下20阶固有振型模态和振动频率云图，表2展现的是前12阶固有频率及振型数据。

根据现场测试结果分析可知，振动筛工作的实际频率为14.7 Hz，故可确定文中关心的阶数为7～9阶，其对应的模态云图如图2所示。

通过观察分析，在最靠近工作频率14.7 Hz的8阶模态(15.101 Hz)下，筛子的最大位移出现在前后挡板和激振器下的筛板处，也就是说这几个部位为筛子工作时最接近共振点的位置，容易形成破坏。

1.8 谐响应分析

振动参数：通过电机型号得知其转速为1 440 r/min，经过减速装置1.68∶1的减速后，传动轴的转速为882 r/min，通过公式计算得出其工作频率为14.7 Hz。

f=n/60=14.7 Hz

a-7阶；b-8阶；c-9阶图2 第7、8、9阶振型模态云图

添加激振力：由于激振器具体的偏心块质量和偏心距数据无法获取，只能参考类似振动筛激振器的数据加以计算获取激振力的大小。通过激振器型号得知偏心块质量m，偏心距e，由公式计算得到激振力为1 250 kN。

P(t)=P0sin(ωt)和公式P0(t)=meω2

式中：P0(t)—激振力；ω—激振器的转动角速度；m—偏心块质量；e—偏心块偏心距。

谐响应分析：通过对整个振动筛的谐响应分析，并以4个减振支架为研究对象，分别计算了其在振动筛工作频率下整体和X、Y、Z3个方向上的振动幅值，得出在工作频率下系统各部件的振动情况，为后续对整个工况诊断系统搭建时传感器位置的确定提供了必要的参数依据。

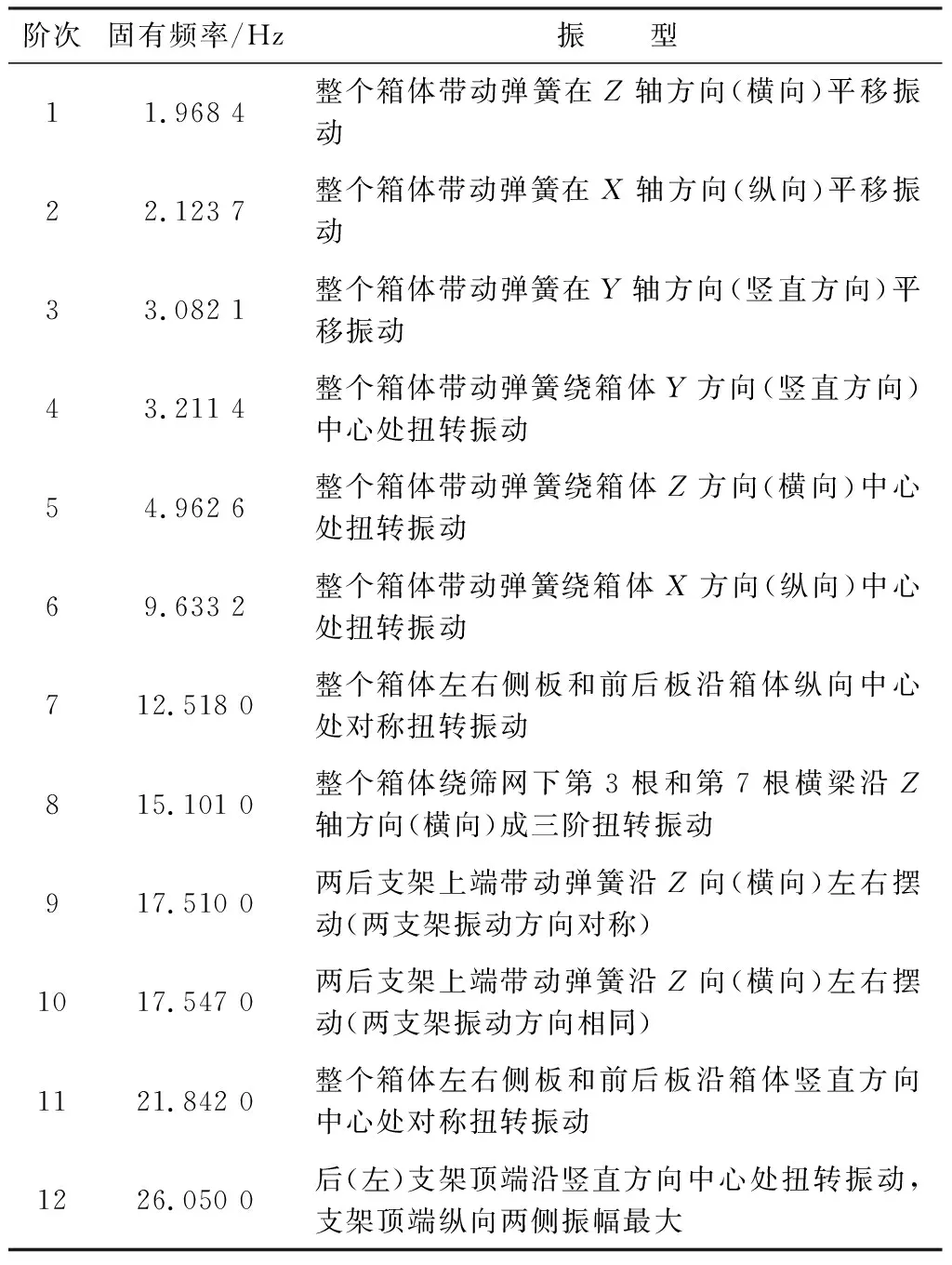
表2 前12阶固有频率及振型

2 模态试验

对于某一个机械系统，可以用系统的固有频率，振动形式和震动阻尼来描述其动态特性，与模态刚度和模态质量一起通称为机械系统的模态参数。模态参数的获得方式主要有2种：一是对激振试验采集的振动数据进行处理识别获得，二是采用有限元的方法对结构进行简化后获得。模态试验分析就是通过试验数据求取模态参数的方法，要想获得高质量的模态参数就要求保证试验条件、数据分析处理的精度和测试仪器的精度全部符合要求。

结合有限元分析软件ANSYS，并通过工程软件SolidWorks对整个振动筛进行参数化建模，并获得筛箱的各阶固有频率和主振型，但由于在建模过程中对局部细节的一些简化，以及边界条件的近似确定与实际情况具有一定的差异性，导致理论分析的结果与实际总是存在误差，所以此方法只有与试验分析相结合，才能将模态分析的优越性充分发挥出来[8]。

2.1 试验仪器和系统

模态试验中所用的试验仪器见表3，试验系统如图3所示。

图3 试验系统图

表3 模态试验仪器列表

2.2 测点选择与布置

对于需要得到模态振型的试件，测点选取原则如下：①避开各阶振型节点；②在基本反应测试件轮廓的前提下，测点尽量少；③结构的次要部分稀疏，主要部分密集；④整个测点的连线构成的图形要保持测试系统的基本几何特点。

本次试验在现场将整个测量点布置在箱体的侧板上。

2.3 试验数据分析

如图4、图5所示是通过锤击分析软件，并根据2组测试数据，所获得振动筛在50 Hz内的固有频率。

图4 频率值为2.004 Hz时的测试结果

图5 频率值8.228 Hz时的测试结果

通过图中数据分析可知，实验获得的最低频率为2.004 Hz，与理论分析结果的1.968 4 Hz基本一致，充分说明前期建立的数学模型比较符合实际情况。

2.4 结构阻尼分析

阻尼及阻尼比：阻尼是使自由振动衰减的各种摩擦和其它阻碍作用。阻尼比指的是结构阻尼系数与结构临界阻尼系数之比，是结构标准化的阻尼大小的表示方式，表示某一结构在受外界激振后自身振动的衰减模式[9]。阻尼比是结构的动力特性之一，主要用来表达结构阻尼的大小，作为描述结构在振动过程中某种能量耗损的术语。以下几方面内容均可以引起结构能量耗散：①支座与筛机联接处、节点的阻尼；②筛机材料及弹簧材料阻尼；③通过支座基础散失一部分能量；④周围空气，水流等介质对振动的阻尼。

振动状态：当激振力作用于整个振动筛系统时，系统的振动状态称为受迫振动。由激振器激振力的类型决定了整个系统是在简谐激振力作用下的受迫振动[10]。

理论分析模型：采用一个小阻尼单自由度的振动系统如图6所示，代表SLO 3673振动系统，可以看作是一个在单自由度机械振动系统中的振动体，通常是质点、定轴转动刚体和平面运动刚体等，由于筛机是一个平面运动的刚体，可以将整个振动筛系统简化为一个等效质量块和一个等效弹簧的系统[11]。

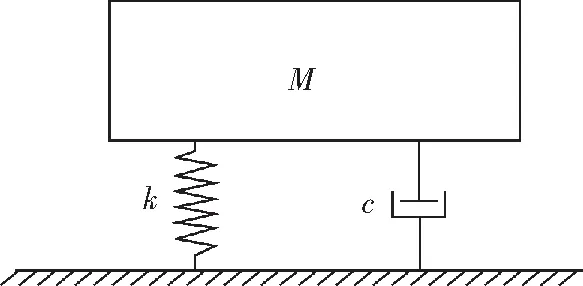
图6 简化系统模型

系统阻尼比计算：对于单自由度衰减响应中计算阻尼比，主要用文献[12]的公式，计算结果见表4。

实验数据：通过二次积分并修改积分后的一次项和二次项获得Y向加速度信号，截取部分有效数据如图7所示。

表4 阻尼比计算结果

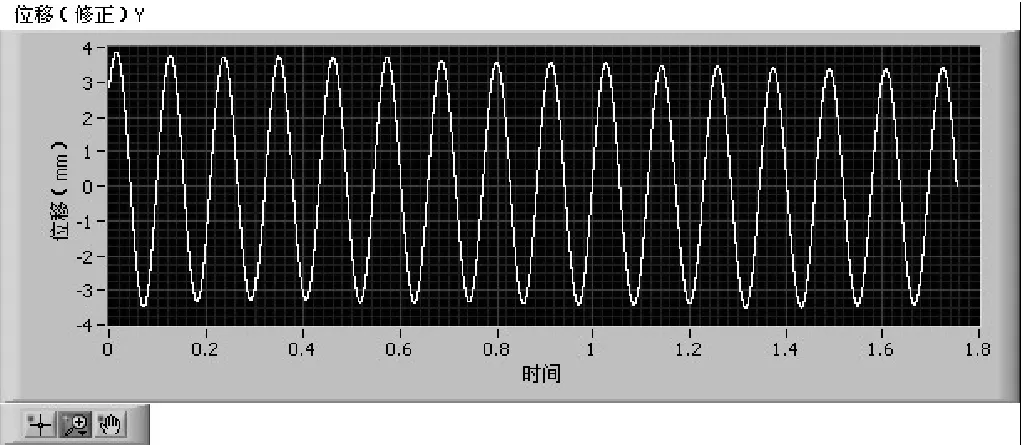
图7 Y向部分位移图

稳态受迫振动：由于阻尼的存在，导致伴随自由振动，并且自由振动都会随着时间的推移而减弱直至消失，留到最后的只有稳态的受迫振动。稳态受迫振动的振幅的大小在工程技术上意义十分重要。可用以下公式表示[13]。

式中：β—放大因子和动力学系数，它是阻尼比和频率比2个变量的函数；λ—频率比，激振力频率与固有频率之比，将阻尼比ζ视为参量，则可得到一系列ζ值的β-λ曲线，如图8所示。

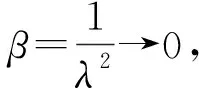
图8 幅频特性曲线

3 结语

通过理论结合试验的方式，构建振动筛工作三维仿真模型，估算理论上的振动筛固有频率和振型，指导振动筛试验台进行模态试验，得到符合实际运行情况的主振型、固有频率和阻尼比，并通过固有频率及阻尼比的分析得出了阻尼比对整个筛机的振幅影响非常小，几乎可以忽略不计的结论。