学生积累探究经验需靠“悟”来完成
江苏苏州市苏州工业园区星洲学校(215028) 张莎莎
思悟是积累经验、积淀数学思想的有效途径。在教学中,光靠教师的教,是无法让学生对知识入脑入心的。教师应对活动探究不断进行反思和革新,来引导学生对学习自主思悟。
一、让学生在操作中“悟”
操作经验是在具体的学习情境中提炼出的,设计符合实际且有一定思维难度的情境操作,能激起学生的主动探索欲,让学生在操作中思悟数学思想的构建。
例如,在“分数四则混合运算”的操作活动教学中,我对例题进行改编:把一个长方形的长和宽分别增加,面积变为原来的几分之几?题中没有给出长方形的具体长和宽的值,这就需要学生在操作中思悟方法,最终汇总出四种解题方法(过程略)——(1)赋值法:先赋原长方形的长和宽是某个具体数值,再依题意计算两面积之比;(2)代数法:设原长方形的长和宽分别为a、b,根据题意再求出两面积之比;(3)图解法:把原长方形的长和宽均分成2份,那么现长方形的长和宽分别多出1份,变成了3份(如下图1);(4)倍率法:把原长方形的长和宽看作两个单位“1”,再依倍率计算两面积之比。
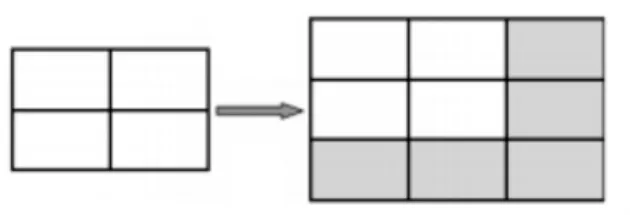
图1
我让学生经历从抽象到形象,从一般到特殊的思维,在操作体验中探索规律,并思悟出多方证实的方法,如此,学生的学习探究经验在“悟”中得到沉淀和升华。
二、让学生在评议中“悟”
同样的探究活动,对不同的学生来说会产生经验积累上的差异。教师组织学生在探究活动中交流、评议,能让学生在“悟”中相互取长补短,丰富探究经验。
例如,在探究“三角形的内角和”的教学中,我给出三种探究方案让学生进行评议。方案一:从特殊到一般,如先求出直角三角形内角和为180°,再推导出一般三角形内角和也为180°。学生反驳:应分别探究三种三角形的内角和都符合这个定律时,才能下结论。方案二:用量角器测量三角形的三个角的度数,相加后得出三角形的内角和为180°的结论。学生反驳:测量存在误差,不能以偏概全。方案三:把三角形的三个内角拼凑在一起组成平角。学生反驳:切割重组法只适用于研究三角形和四边形的内角和,假如研究对象是多边形(边数≥5)就行不通了,因为其内角和超过周角,无法看出度数。有学生建议:可以把多边形分割成一个个小三角形……
学生在相互评议和思维交锋中,看待问题更加客观、理性、全面,使探究方法逐步一般化、精确化、简单化,在“悟”中不断完善和提升探究经验。
三、让学生在运用中“悟”
学生积淀的探究经验只有不断地被激发和运用,才能使“悟”在不断叠加的学习经验中得到巩固和深化。
例如,在教学“解决问题的策略”时,在学生学习了“一一列举”的策略后,为巩固应用我出示三组问题:
(1)李大婶要用30米长的竹篾材料围一个篱笆,怎样围面积最大?
(2)李大婶要用300米长的竹篾材料围一个篱笆,怎样围面积最大?
(3)李大婶要用30米长的竹篾材料围成一个宽为7米的长方形篱笆,这个篱笆的面积是多少?
师:打算用什么策略来解决这三组问题?
生1:对于问题(1)和问题(2),可以采用一一列举的策略,但例子样本太大,操作很麻烦。
生2:还可以通过减少竹篾的材料,使例子样本容量减少,找出一般规律,再应用推广。
生3:对于问题(3),直接求解,用周长减去宽,求出长,就可以求出长方形的面积了。
师:如何将问题(3)变为采用“一一列举”的策略?
生4:删去“宽为7米”这个已知条件即可。
我在问题中巩固“一一列举”策略的应用,让学生在“悟”中发展思维,并对学习方法的应用由片面认识转变为全面认识。
总之,教师要根据学生的认知水平、活动经验、迁移能力和心理特征等设计探究活动,让学生高质量地落实探究经验,并结合“悟”“做”“议”“用”等环节,使探究经验和数学素养丰富充实起来。

