找准根源 对症下药 拨云见日
——一年级上册“解决问题”学生典型错误研究
浙江杭州市萧山区瓜沥镇任伯年小学(311241) 赵 菁
一年级“解决问题”的呈现形式是以“用数学”为主,穿插在1~10的认识和加减法的各个单元中。学生识字量少,解决问题所用内容大多是图片,伴以少量文字。每每教学一节“解决问题”课,学生都表现得非常积极,对于教师提出的问题也都可以轻而易举地回答。但在课后独立完成作业或练习时,学生的错误率却特别高。
为什么会这样?究竟学生在“解决问题”时出现了哪些问题,遇到了哪些困难?对此,我找准根源,对症下药,拨开数学解决问题上的“乌云”,看见了明媚的“阳光”。
一、从图到文,准确读懂题意
教材用有层次的三句话,对学生用数学知识解决问题的过程给予了明确指导,引导学生体会解决数学问题所要经历的步骤,体会从图到文解决问题的基本方法。
1.三次读题,读清题意
(1)第一次读,知道讲的是什么。一年级学生识字量少,读题时生字是一个很大的障碍,理解上有很大的困难。因此呈现文字题时,必须给学生不认识的字注上拼音,带领学生认读,对学生不理解的生字和词语要进行解释。待学生看到生字不再害怕了,再慢慢放手,让学生独立读题。
(2)第二次读,圈出关键字、词。读题时,要善于抓住题中的关键字、词,读懂它表示的真正意思。只有反复读题,仔细琢磨,认真推敲,才能更好地理解题意。为了强化学生认真审题,我要求学生一边读题,一边把关键字、词圈出来,这样学生在分析时就会一目了然,提醒自己注意。
(3)第三次读,筛选图中信息。一年级学生收集信息的能力比较薄弱,眼花缭乱的图片常常会分散他们的注意力。对此,可引导学生从问题出发,从众多信息中筛选出与问题关联的数据信息。利用书本上的主题图,多次进行练习,可逐步培养学生的信息收集和处理能力,为解决问题奠定基础。
2.筛选重点,学会分析
看懂图意后,要开始分析图中的有用信息,包括数字、文字、大括号和问号等,并进行分析、整合和梳理。
二、扫除思维障碍,厘清数量关系
一年级学生的思维以直观为主,一些学生的认识水平仅仅停留在“求还剩多少就用减法”的直观层面上,没有抽象形成“总数-部分数=部分数”的数学思维模型。为了打破学生出现“看关键字定方法”的习惯思维,可引导学生对比题组信息的区别和联系,使学生在对比中自觉揭示各部分信息之间的关系。
图文并用型。有些习题(如图1)图中配有文字,可以帮助学生读懂题意,也有很多表示动态的词语,比如“摘了”“游走”等。圈出这些帮助性词语,可助学生理解“求部分”的问题。
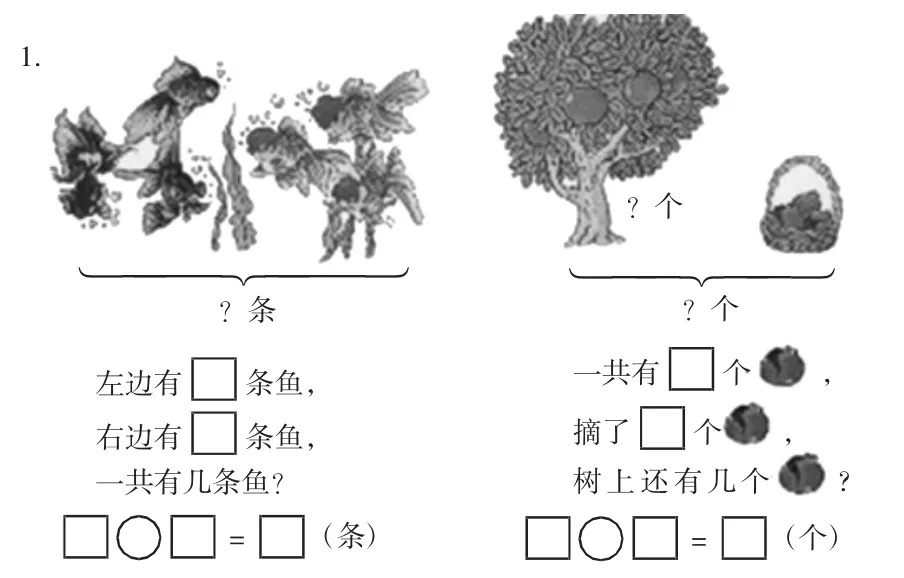
图1
若隐若现型。若隐若现型题,学生最容易受干扰。有些学生会直观地去数一数,忽视从整体去观察题目。我们就要借助这个“若隐若现”,让学生在争论中明白,正因为看不清数不清,才需要大家用计算来解决。这样可强化学生对“求部分”问题的认识。

图2
深藏不露型。如图3这类题目,要求的部分完全未知,没有可依托的图案,也没有像“摘走”“跳走”等明显的词语。这时就需要学生独立思考,搜集信息,分析条件是什么,要求什么。
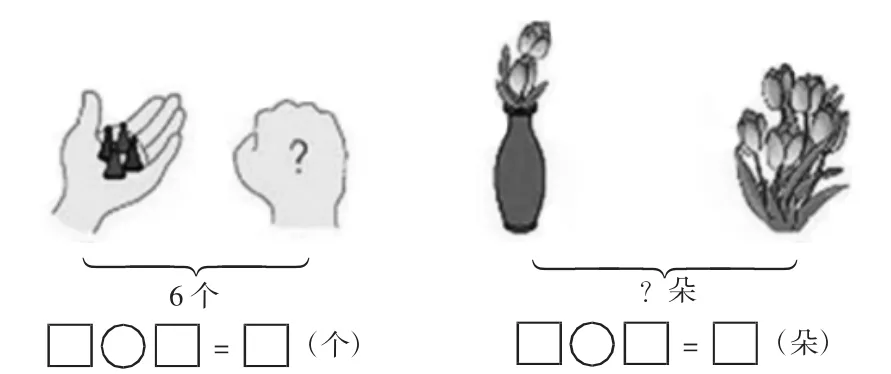
图3
一题多变型(如图4)。图画中不同的符号,代表了不同的含义。相同的符号,在不同的位置意义也不同。借助符号,构建加减法的模型,有利于学生更好地理解算理。

图4
三、认真仔细做题,养成良好解题习惯
在解决问题的过程中,学生完成了如下两个转化。

学生看到“一共”就用加法,看到“还剩”就用减法,是疏于对算法的理解,不利于学生思维的发展。教学时,教师要有意识地引导学生感悟算法,让学生形成解决问题的方法和策略。同时在学生做完题目后要引导其仔细检查,养成良好的解题习惯。
1.深入感悟算法,形成解题策略
(1)剖析整体和部分关系,归纳算式
两个部分可以合并成一个整体,一个整体可以分为两部分,在整体中去掉一部分,就剩下另一部分。求整体(总数),就把两部分合起来,用加法算,即“部分数+部分数=总数”。求部分数,则应从整体中去掉另一部分,用减法算,即“部分数=总数-部分数”。
(2)归纳整理题型,掌握方法
在梳理以上“解决问题”的各种题型的基础上,我们还应整理归纳出常见的“解决问题”经典题型。这样,不仅方便学生更好地理解题型,掌握解题的方法,而且更容易找出学生的易错点,纠错起来更有针对性。
2.帮助学生对比梳理,明确错因
针对学生易错类型,及时进行整理分类,分析错因。在低年级的“问题解决”中,情境图常用大括号和问号的形式来表示所要求的问题。对此,我们可以通过同一个情境的不同类型,让学生关注问号的位置并对比分析,理解题意。通过比较,让学生理解“问号位置不同,图意就不同;相同的数字在不同的位置,代表的含义也是不一样的”。
综上,在低年级的“问题解决”教学中,我们应从学生的认知基础和年龄特征出发,让学生在情境图中学会看图、学会读题,并在此过程中建立数学模型,理解数量关系,总结解决问题的方法,养成良好的学习习惯,为后续的学习打下坚实的基础。

