一个代数恒等式的妙用*

2014 (200241)

一、代数恒等式

这样一个小小的恒等式在证明一些不等式时却有大大的作用.它的好处在于可以化轮换对称式为对称式，可以化对称式为轮换对称式，还可以将一种轮换对称式变换为另一种轮换对称式.下面举几个例子进行说明.

二、应用

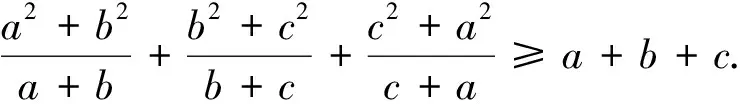
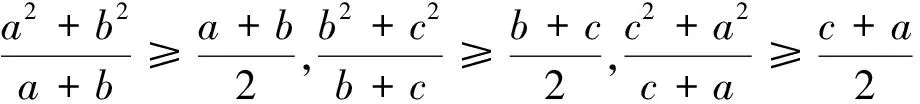
其他两个不等式同理可以证明.

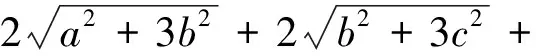
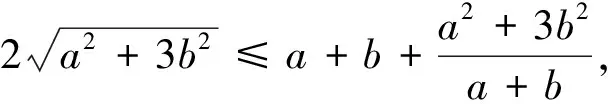
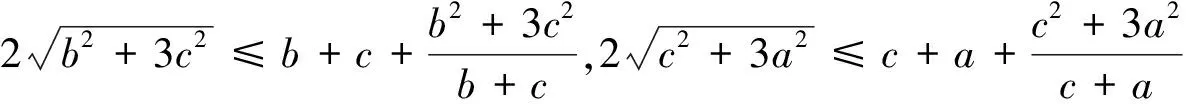
注：这个不等式容易推广到一般情况：

已知a、b、c、m、n∈R+，a+b+c=3，求证：

还可以进一步得到：

已知a、b、c、m1、n1、m2、n2、m3、n3∈R+，a+b+c=3，m1+n1=m2+n2=m3+n3=k，求证：

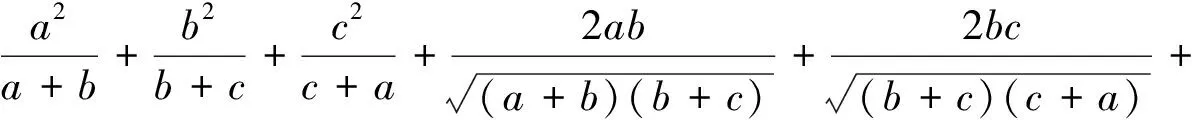
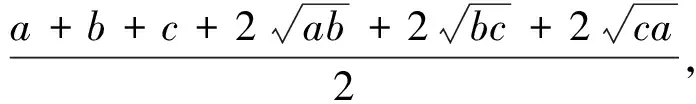
下面证明

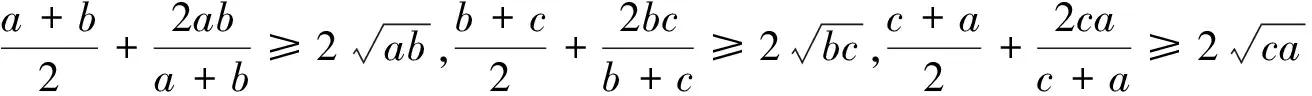
上式显然成立.

例4 已知a、b、c∈R+，求证：

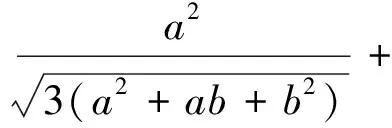
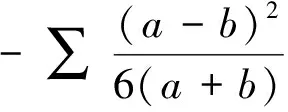
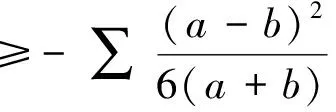
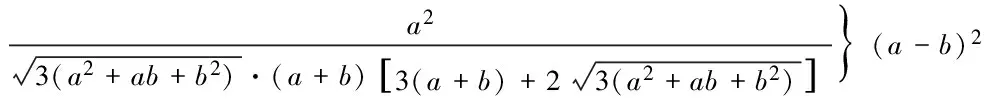
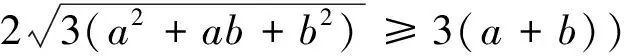
显然成立.

注：受例4启发，提出一个问题：

已知a、b、c∈R+，当λ与μ满足什么条件时，下面不等式成立：