用于短时定位的MEMS旋转调制惯性导航系统*
贾 勇,秦永元,李岁劳,侯 震
(西北工业大学自动化学院,西安 710129)
惯性导航系统INS(Inertial Navigation System)以其自主性强、隐蔽性好及抗干扰的优点,广泛应用在航空、航天、航海和车辆导航等领域,但INS的不足是导航误差随时间积累,其中惯性器件常值误差是主要误差源[1-2]。MEMS惯性器件因其体积小、功耗低、重量轻、反应快、精度高及成本低,也被广泛应用,特别是航空和车辆导航领域,但因MEMS惯性器件的零偏重复性和零偏稳定性大,限制了它们的应用范围[3-4]。
由MEMS惯性器件组成的惯性测量单元IMU(Inertial Measurement Unit)常采用进行精确的标定[5]、采用合适的滤波算法[4]或与其他传感器(如GPS)组合[6-7]等方案,使其具有更好的实用能力。但上述方案具有一定的局限性,一旦条件不满足,MEMS惯性导航系统的性能将不能得到保证。旋转调制技术则不存在限制条件,只需在合理的转动方案下带动IMU转动,便可实现导航误差的自补偿[8-9]。随着MEMS-IMU精度的提高及旋转系统成本的降低,将旋转调制技术引入到惯性导航领域,将实现低成本高精度的导航定位[10-11]。在已有的研究中,[8-9]仅停留在理论分析及仿真验证阶段,[10-11]则仅将MEMS-IMU放置在高精度转台上,价位过高,并不实用,且导航时间选取过长,误差很大。本文正是在上述应用背景和行业现状的情况下,将旋转调制技术应用到MEMS-INS中,使MEMS旋转调制RM(Rotation Modulation)惯性导航系统达到短时导航定位能力,并将其应用到实际工程项目中。同时,本系统成本低廉、性能可靠,适合相关专业开展实验教学使用。
1 短时导航性能分析
对于MEMS-INS,在短时间工作时,重力场和地球表面曲率半径的变化对惯性导航系统误差的影响可忽略[1]。由于本系统选用的MEMS-IMU无法感测到地球自转角速度ωie,故忽略地球自转角速度ωie产生的交叉耦合项。因此水平通道误差模型简化为:
北向通道:
(1)
东向通道:
(2)
当考虑初始姿态/航向误差、速度误差时,可以得到更完整的误差模型。根据式(1)~式(2)推导得到完整的水平通道短时导航误差表达式如下:
姿态/航向误差表达式:
(3)
速度误差表达式:
(4)
位置误差表达式:
(5)
通过对式(3)~式(5)分析可得:在短时导航时,对系统精度影响最大的是水平方向的陀螺常值漂移和加速度计的零偏,其次是初始姿态误差。
为此,在捷联惯性导航系统基础上,本系统通过引入旋转调制技术来控制惯性器件有规律地绕Z轴进行旋转,从系统级角度实现惯性器件误差自补偿[8]。
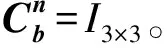
(6)
若陀螺和加速度计存在常值误差εs、s,在t时刻,两项常值误差在导航坐标系(n系)的表达式为:
(7)
(8)
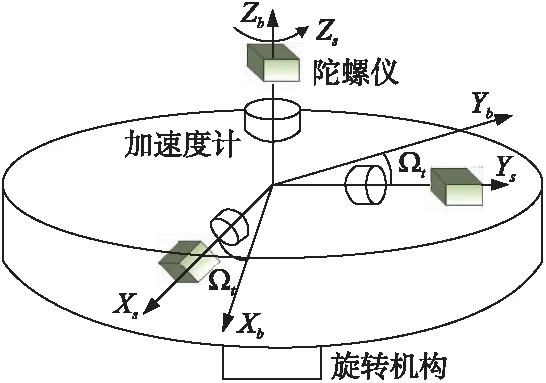
图1 MEMS-RMINS系统构架
一方面,在短时导航情况下,影响系统性能的主要是水平方向的陀螺常值漂移和加计零偏;另一方面,航向方向陀螺和加计不受调制,且对导航性能影响也很小;同时,系统初始误差不受调制[1],且部分耦合项影响小。因此,忽略影响小的耦合项,仅推导水平方向的陀螺常值漂移和加计零偏引起的导航误差。由式(1)~式(2)及式(7)~式(8)可得,旋转调制后,系统的主要短时导航误差表达式如下:
姿态误差表达式:
(9)
速度误差表达式:
(10)
为了更直观地分析旋转调制技术的特点,下面以陀螺仪为例进行仿真分析。仿真条件为:陀螺常值漂移εx=εy=20(°)/h,旋转角速度Ω=20(°)/s,旋转方式为单向连续旋转,仿真时间t=100 s。仿真结果如图2所示。
对比图2(a)~2(b)可知:当引入旋转调制技术后,水平方向陀螺和加速度计的常值误差对姿态、速度的影响被调制成正弦形式,误差不再发散。旋转调制技术使得常值误差的积分在整周旋转中为零,实现误差自补偿,常值误差不再成为影响导航精度的主要因素,从而导航性能大幅提高。
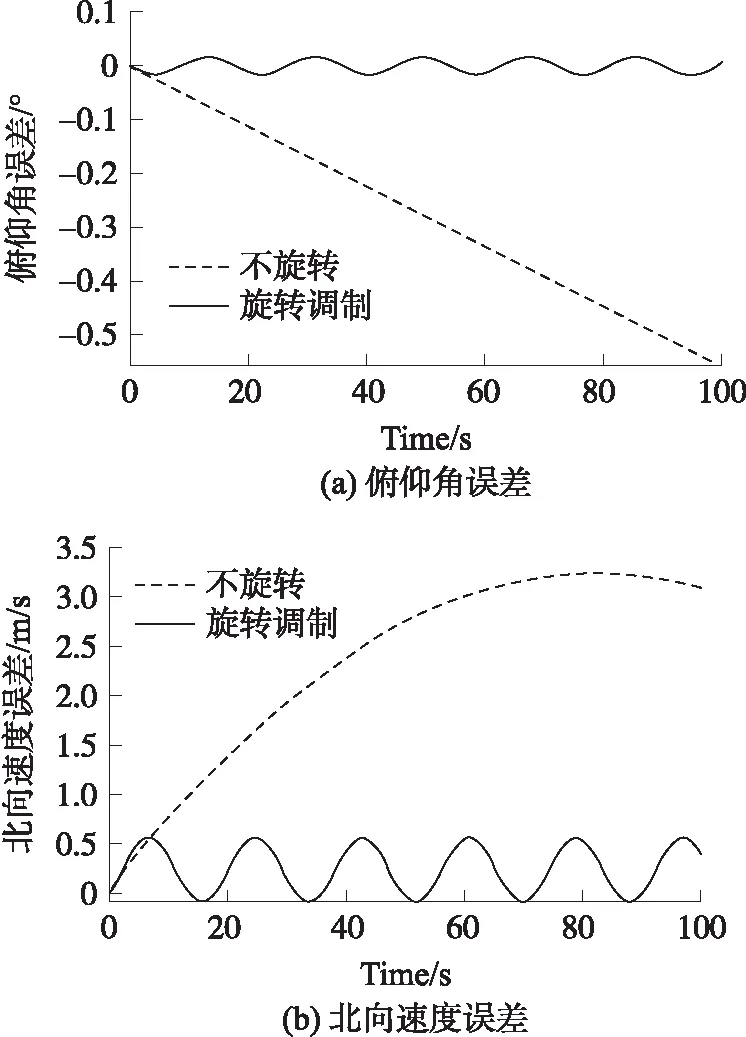
图2 旋转调制效果图
2 系统介绍
2.1 系统组成
根据第1节的分析,设计的实际系统如图3所示。系统主要由MEMS-IMU、旋转机构(直流力矩电机、光电编码器及机械结构)、控制器及电机驱动器四部分组成。

图3 MEMS-RMINS实物图
2.2 旋转方案及导航解算方案
2.2.1 旋转方案的选择
旋转调制惯性导航系统常选用单向旋转、正反整周旋转及转停方案3种旋转方案。本部分首先从误差抑制的角度分析这3种方案的调制效果。假设x、y向陀螺漂移相等,即εx=εy,且初始时刻x、y陀螺敏感轴分别指东和指北,由式(9)~式(10)可得地理系下的等效北向陀螺漂移、姿态角误差及北向速度误差为:
(11)
以下对3种方式的旋转调制效果进行仿真对比。仿真条件与第1节相同,仿真结果如图4所示。
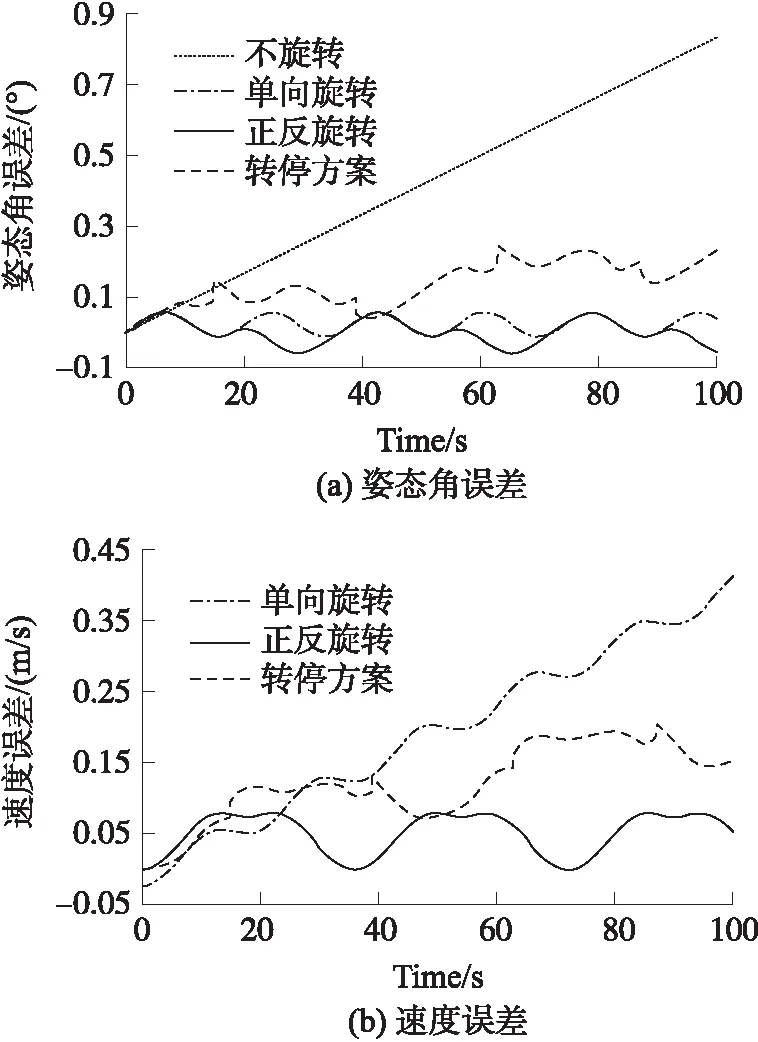
图4 3种旋转方案调制效果
从图4曲线可以看出:引入旋转调制技术后,3种方案的姿态误差均得到有效抑制,前两种旋转方案的误差最大值相等,但在相同的时间内,正反整周旋转的姿态误差均值更小;同时正反整周旋转在速度误差上,均小于其他两种旋转方案。
同时,单向旋转方案要求系统配置导电滑环,导电滑环不仅会影响INS的可靠性,还会增加系统的成本,且陀螺始终敏感单向的电机旋转角速度耦合误差,因而对误差角的标定提出了更为苛刻的要求。转停方案则要求精确的多位置变换,在一个旋转周期内需要频繁地控制电机的启动和停止,一方面增加控制难度,另一方面旋转周期往往比连续旋转长。正反整周旋转则能很好地解决上述两种方案存在的问题。
综合上述,本系统选择正反整周旋转方案。
2.2.2 导航解算算法
引入旋转机构后,系统导航解算算法也相应发生变化。由于存在角速度误差δω及角位置误差δφ,若选择的导航解算算法不合适,会降低系统性能。旋转调制惯性导航系统常采用两种解算算法:角速度调制型算法和角度调制型算法[12]。
对于角速度调制型算法,捷联矩阵更新在载体系和地理系之间进行。通过分析可知,由δω及δφ引起的载体坐标系相对惯性坐标系的角速度误差在载体坐标系下的投影为:

(12)
式中:角位置误差一般为小量,因此cosδφ≈1,sinδφ≈δφ,化简式(12)可得:
(13)
同理,加速度计误差在载体坐标系下的投影为:
(14)
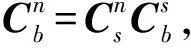
由于本系统选择的测角器件分辨率有限,其理论上的极限控制精度有限,会产生较大的δω及δφ,因此,本系统选择角度调制型结构。
3 误差分析及补偿
加入旋转机构后,与捷联惯性导航系统相比,误差传播形式更加复杂,除了具有捷联惯性导航系统的误差特点,还存在新的误差类型。新的误差类型主要包括:旋转轴与径向敏感轴的不正交角、电机轴的安装偏角及径向敏感轴的零位不重合角。
3.1 旋转轴波动
由于旋转轴与径向敏感轴的不正交角与电机轴的安装偏角耦合在一起,共同对系统产生影响,将其称为旋转轴波动。旋转轴波动的详细分析及标定补偿结果参考本课题组发表的论文[13-14]。下面仅将在实验室条件下计算得到的y轴倾角显示如图5所示。
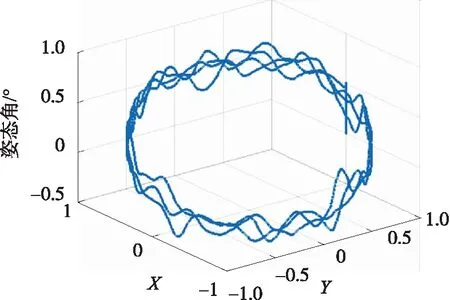
图5 旋转过程中的实测波动曲线
3.2 径向敏感轴的零位不重合角
径向敏感轴的零位不重合角Δφx和Δφy产生于IMU内部敏感轴不正交角、IMU固定在旋转平台上存在的安装偏角等因素。
假设光电编码器输出为零时,x、y陀螺敏感轴与机体坐标系X、Y间的不重合角为Δφx和Δφy。当载体绕Y轴有输入角速度ωY时,陀螺敏感轴方向的实际角速度为:
(15)
经过坐标变换后得到机体坐标系的角速度为:
(16)
对于捷联惯性导航系统,Δφx只对x轴有影响,Δφy只对y轴有影响;而对于本系统,当Y轴有输入角速度时,在两个轴上将产生由Δφx和Δφy共同影响的角速度误差;同时,两个轴上的误差还存在二倍角频率的误差分量。
为此,在实验室条件下对Δφx和Δφy进行标定:通过采集光电编码器和陀螺输出,根据式(15)进行曲线拟合,得到的标定结果如表1所示。从表1 可以看出,不重合角具有很好的重复性。

表1 零位不重合角标定结果
4 实验验证及结果分析
为了验证旋转调制技术的误差抑制效果及实际提高的定位精度,本节分别对静态实验和动态实验进行分析,并对动态实验进行不同时间长度下的精度评估。
4.1 静态实验
静态实验在惯导实验室的双轴位置转台上完成。首先将转台调平,并使MEMS-RMINS的指向大致为东北天。系统在不旋转NR(Non-rotation)及旋转情况下,分别进行了3次实验,实验结果中的最大位置误差如表2所示。
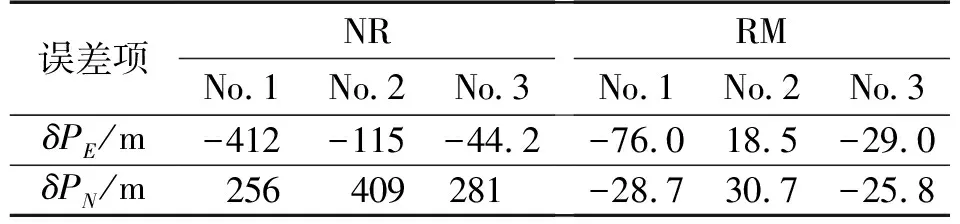
表2 100 s静态实验最大位置误差比较
两类实验的第2次实验结果详细对比曲线如图6 所示。从图6可以看出,原本误差随时间增大的MEMS-INS,在引入旋转调制技术后,位置误差得到抑制。从表2可知:其东向和北向位置误差精度最大提高了21.33倍和15.83倍,最小也提高将近 1倍和7.35倍。实验结果说明本系统采用的旋转调制技术及解算方案的正确性及可行性。
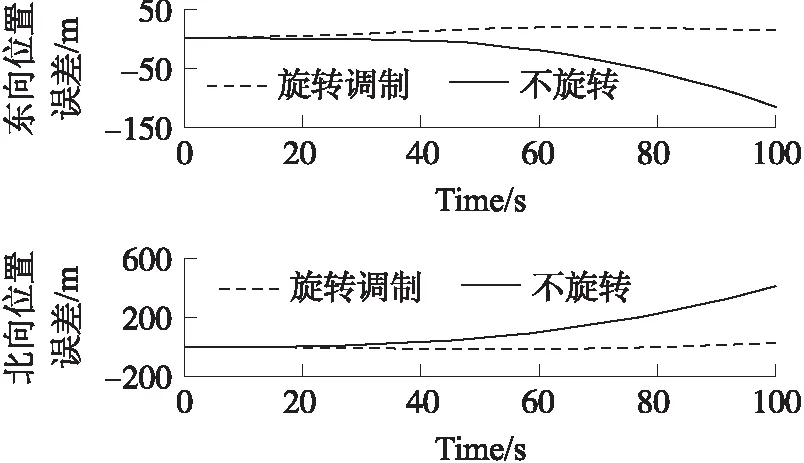
图6 静态实验位置误差
4.2 动态实验
动态试验在本校东门区域进行;不同系统(包括参考系统、MEMS-INS、MEMS-RMINS)得到的路径如图7所示;位置误差对比如图8所示。图8中表示的东向和北向位置是相对于车辆起始点的位置(图7中的五角星所示)。
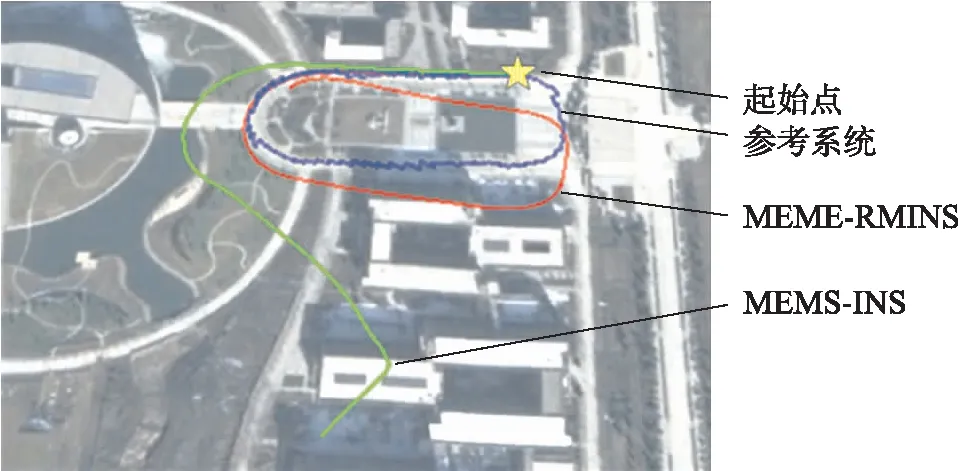
图7 实测轨迹对比
从图7、图8可得,随着时间的增长,MEMS-INS的位置与参考系统相比,误差值和误差偏离程度不断增大,且东向和北向位置误差最大值分别达到106.2 m、273.6 m;而MEMS-RMINS的位置与参考系统相比,误差值则增加缓慢,轨迹能很好的重合,且东向和北向位置误差最大值仅为20.56 m、38.56 m。在100 s动态实验下,MEMS-RMINS最大误差精度分别达到MEMS-INS的5.17倍、7.10倍。
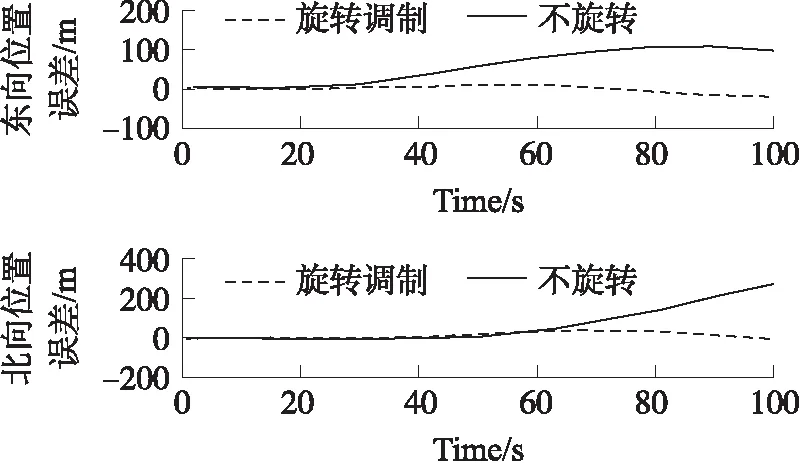
图8 动态实验位置误差
4.3 短时定位分析
为更详细的得到MEMS-RMINS的短时定位特性,以其一个旋转周期为时间起点,时间范围依次增长,分析MEMS-RMINS的位置误差增长特点。如表3 所示,随着导航时间的增大,MEMS-RMINS的位置误差也不断增大,但与MEMS-INS相比,增长速度明显较慢,当时间到达72 s时,东向和北向位置误差最大值的精度分别达到17.6倍和2.51倍。

表3 短时定位最大位置误差比较
同时,采用文献[15]所述的TRMS精度评估方法,计算动态实验时不旋转与旋转状态下的不同导航时间下的TRMS值。具体计算结果如表4所示。通过表4的计算结果可以得出:经过旋转调制后,MEMS-RMINS的短时定位精度在不同时间长度下,均得到提高,与MEMS-INS相比,平均精度能达到2.95倍。在导航时间小于36 s的情况下,TRMS小于15 m,完全能满足部分应用场合。
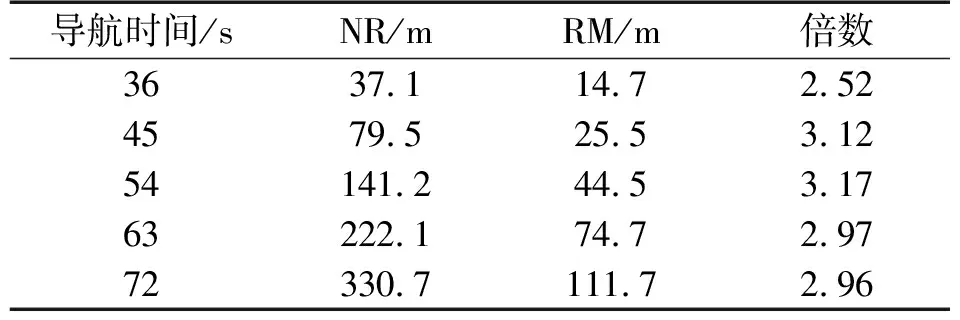
表4 旋转前后TRMS计算结果
5 总结
在短时定位时,MEMS惯性器件误差很大,会使定位误差随时间快速积累,而旋转调制技术能有效地抑制这种误差发散的特性,从而提高MEMS-RMINS的短时定位精度。从理论分析、仿真结果及实验结果可以得出以下几点:
①短时导航时,MEMS惯性器件的常值误差是主要误差源,而旋转调制技术能有效地消除常值误差对系统性能的影响。
②对于MEMS-RMINS,选择正反整周旋转方案及角度调制型算法更合适。
③旋转机构引入后,将产生新的误差,需根据误差特点进行曲线拟合,得出误差系数并补偿,以减小旋转机构引入的误差。
④静态实验时,旋转后的定位精度是不旋转的10倍左右说明旋转方案、解算算法及补偿方法的正确性和可行性。动态实验时,旋转后的导航精度是不旋转的3倍左右说明旋转调制技术在实际应用中也能提高定位精度,在惯性导航领域具有实际应用价值。
⑤由于系统工作环境的变化以及存在未考虑到的误差因素,导致系统性能下降,这需要在以后的研究中做进一步分析。
本系统已用在实际的工程项目中,并取得了良好的效果。而随着MEMS惯性器件精度的提高、旋转方案及导航算法的改进,MEMS-RMINS在短时定位领域的应用将越来越广。并且,该套系统已经在我校惯性技术等课程的实验教学中得到应用,教学效果良好。
参考文献:
[1] 高钟毓. 惯性导航系统技术[M]. 北京:清华大学出版社,2012:250-253.
[2] 秦永元. 惯性导航[M]. 北京:科学出版社,2014:1-4.
[3] 李博文,姚丹亚. 低成本车载MEMS惯导导航定位方法[J]. 中国惯性技术学报,2014,22(6):719-723.
[4] 王丁伟,祖家奎,黄海. 基于MAEKF算法的航姿参考系统设计[J]. 传感技术学报,2017,30(2):319-325.
[5] 刘一鸣,李杰,刘秀峰,等. 一种加速度计的标定补偿方法研究[J]. 传感技术学报,2016,29(12):1846-1852.
[6] 刘强,王昌刚,刘玉宝,等. 基于MEMS/GPS的航向姿态测量系统设计[J]. 传感技术学报,2016,29(8):1290-1296.
[7] Sheng H L,Zhang T H. MEMS-Based Low-Cost Strap-Down AHRS Research[J]. Measurement,2015,59:63-72.
[8] Sun W,Wang D X,Xu L W,et al,MEMS-Based Rotary Strapdown Inertial Navigation System[J]. Measurement,2013,46:2585-2596.
[9] Qin Y,Lai J,Wu Q,et al. MEMS Rotary Strapdown INS with Low-Resolution Rotary Encoder[J]. Gyroscopy and Navigation,2016,7(4):311-317.
[10] Du S. Rotary Inertial Navigation System with a Low-Cost MEMS IMU and Its Integration with GNSS[D]. University of Calgary,2015.
[11] Du S,Sun W,Gao Y. Integration of GNSS and MEMS-Based Rotary INS for Bridging GNSS Outages[J]. Lecture Notes in Electrical Engineering,2015,342:659-676.
[11] 孙尧,王庭军,高延滨,等. 旋转式捷联惯导系统解算结构[J]. 中国惯性技术学报,2013,21(1):10-15.
[12] Jia Y,Li S L,Xu Y F. Analysis and Compensation of Rotating Shaft Fluctuation on Rotation Inertial Navigation System[C]//2016 IEEE Chinese Guidance,Navigation and Control Conference,2016:609-613.
[13] 贾勇,李岁劳,王玮. 安装误差对旋转式惯导系统影响及补偿[J]. 仪器仪表学报,2015,36(12):2 674-2 680.
[14] 王艳永,贾兴荣,高晖,等. 基于统计推断的惯性定位精度评估方法对比[J]. 计算机应用,2012,32(s2):276-279.

