基于姿态传感器的脊柱形态测量技术*

沈林勇,杭辉冬,赵 检,杨长伟,张 震

(1.上海大学机电工程与自动化学院,上海 200072;2.长海医院,上海 200433)

近年来,脊柱畸形成为影响人类身体健康的又一类顽疾,在青少年和儿童中有较高的发病率[1]。临床诊断中,所有脊柱的冠状面、矢状面或轴向位偏离正常位置,发生形态上异常的表现,统称为脊柱畸形。

目前国内评估脊柱形态的主要方法是影像学方法,包括X线测量、CT测量和MRI测量。现在采用最多的是X线测量,获得简单静态X平片进行分析。虽然X线测量操作很方便,同时价格低廉,但是X线测量较强的放射线,对患者进行前屈后伸位、胸椎和腰椎的正侧位共计8次的X线暴光拍摄,这些暴光将使患者患癌症的概率增加[2]。CT可以观察到许多X线测量无法检测到的数据,Ochia等[3]采用CT扫描的方法测量背痛患者的脊柱节段运动,对患者在不同的仰卧位进行CT扫描并计算出椎体节段的旋转角度和平移量,精度可达到0.1°和0.1 mm,空间分辨率高。但是获取数据的时间较长,重建图像的计算量较大以及具有更大的放射性。MRI测量[4]虽然不具有放射性而且精度很高,但是需要多次扫描,所以不便于实现脊柱形态的日常监测。

国内外展开了非X线测量脊柱形态方法[5-10]的研究。超声测量可以分析脊柱的三维运动,Dvir等[5]的方法是根据不同移动位置以及角度变化之后声波叠加上的时间差,利用三角测量法以及软件计算,可以确定超声波发生器在空间坐标的具体位置,可以推算出颈椎的运动状态。超声波测量方法是一种无创的测量手段,精度和重复性都很高,但是对超声波信号的准确传输要求高。Spine Scan电子脊柱测量仪采用三维电子重力角度感应技术,可实现脊柱侧弯躯干倾斜角(ATI)测量,驼背脊柱矢状面角度测量和身体活动度(ROM)的测量。Spine Scan具有便携、无辐射、实时的特点,但是测量结果从医学的角度不直观,医生使用Cobb角来判断脊柱侧弯和后凸变形严重程度。我们研究基于非X线的脊柱形态参数测量技术,通过姿态传感器测量人体脊柱在体表的形态参数,对所测参数进行解析,获取医学上脊柱形态判断依据Cobb角和拟合的脊柱曲线,为医生的进一步诊断和治疗提供参考依据。

图1 Cobb角的定义和侧凸Cobb角的测量原理

1 Cobb角测量原理

1.1 Cobb角的测量原理

影像学方面对于脊柱畸形的诊断,采用测量Cobb角的方法。即测出侧凸或者后凸脊柱两端(最头端和最尾端)最倾斜的椎体之间成角,是对于任何脊柱畸形最基本的描述。医学对Cobb角的定义为:确定脊柱侧弯和后凸的端椎,上、下端椎(如图1(a)中的T12为上端椎,L4为下端椎)是指侧弯和后凸中向脊柱侧弯凹侧倾斜度最大的椎体。在上端椎的椎体上缘划一横线ac,同样在下端椎椎体的下缘划一横线bc,对此两横线各作一垂直线,两垂线的交角是Cobb角。根据几何关系ac和bc形成的夹角等于Cobb角。

(1)

(2)

所以在人体的站立姿态下,通过测量脊柱在后背面和正侧面的体表形态的位姿角度参数,由上述几何关系可计算出Cobb角数据。

1.2 脊柱形态位姿角度测量

为了感知脊柱位姿,可选用姿态传感器[11-12],将姿态传感器在测量过程中紧贴于人体后背,姿态传感器的姿态变化可以表示脊柱棘突的变化。姿态传感器通过感应脊柱棘突的姿态变化,将姿态数据计算成Cobb角,再经过医学修正,可以得到脊柱Cobb角。

姿态传感器包括三轴陀螺仪,三轴加速度计和三轴磁力计,集成高精度卡尔曼滤波姿态融合算法。姿态传感器可以直接输出三轴的转角包括偏航角ψ(yaw)、俯仰角θ(pitch)和滚转角φ(roll),姿态传感器的坐标如图2所示。姿态角度是相对于地面的姿态,所以需要建立姿态传感器的坐标系和地面坐标系的关系,地面坐标系如图3所示,在地面上选定一点Og,xg在水平面内指向某一方向,zg轴垂直于地面并指向地心,yg轴在水平面内垂直于xg轴。

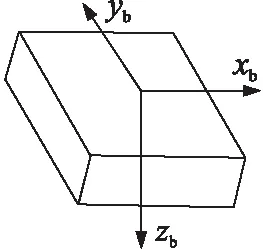
图2 姿态传感器坐标系

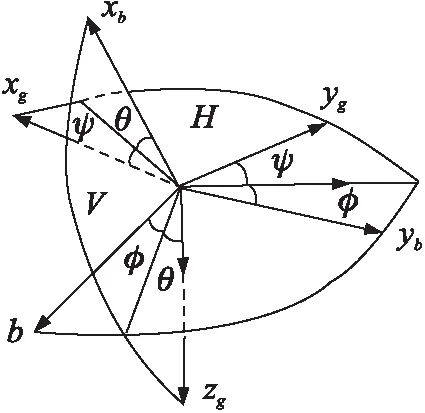
图3 姿态传感器姿态角

传感器坐标系xb轴与水平面的夹角为俯仰角θ,偏航角ψ为传感器坐标系xb轴平面上的投影与地面坐标系xg轴之间的夹角,滚转角φ为传感器坐标系zb轴与通过机体的xb轴的铅垂面间的夹角,姿态角如图3所示。

根据姿态传感器姿态角的特征,将姿态传感器应用于人体脊柱的测量时,俯仰角用于记录被测者脊柱前后凸的变化,即xb与水平面的夹角;偏航角用于记录被测者脊柱侧弯的变化,即xb轴平面上的投影与初始地面xg轴的夹角,如图4所示,在姿态传感器运动过程中尽量保持滚转角不变。

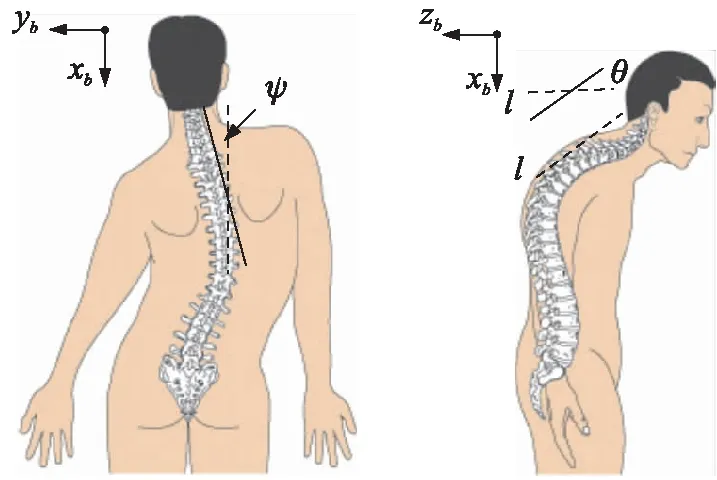
图4 测量时姿态角与脊柱的关系

姿态传感器在测量人体脊柱过程中,每次采集数据时姿态角都会发生变化。对于角度的变化,相当于一个坐标系相对于另一个坐标系做一次或者多次旋转,它们之间的关系可以用方向余弦或者欧拉角表示。若(xb,yb,zb)为仪器在传感器坐标下的坐标值,(xg,yg,zg)为仪器在地面坐标系下的坐标值,由以上两个坐标的关系,如果已知姿态角度为(ψ,θ,φ),则可以得出两个坐标的映射关系:

(3)

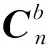
(4)

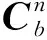
(5)

求反函数得到姿态角的值,但在求解过程中需要注意反三角函数的求解存在多值问题。

1.3 多Cobb角测量的实现方法

测量计算单个Cobb角的方法为:假设测量仪脊柱点T11开始测量,则初始的俯仰角和偏航角分别为θ0和ψ0(逆时针为正),当运动到T12时,俯仰角变为θ1偏航角变为ψ1,同时编码器采集运动距离为l1,在矢状面上可以采集到测量仪运动时的偏航角集合:

ψ={ψ0,ψ1,ψ2,,…,ψn}

(6)

同理也可得冠状面上俯仰角的集合:

θ={θ0,θ1,θ2,…,θn}

(7)

根据Cobb角的定义条件,将集合ψ按照正负号变化分为两个子集合ψ′和ψ″:

ψ′={ψ0,ψ1,ψ2,…,ψi}

(8)

ψ″={ψi+1,ψi+2,ψi+3,…,ψn}

(9)

式中:ψi为偏航角出现正负符号变化的节点。

判断子集的符号,情况1:ψ′为正值,ψ″为负值时,Cobb角的计算公式为:

(10)

情况2:ψ′集合中的值为负值,ψ″中的值为正值时,侧凸Cobb角的计算公式为:

(11)

同理对于前后凸中的单个Cobb角的计算方法与侧弯Cobb角的计算方法相同。

在人体脊柱实际测量中存在多个Cobb角,对于多个Cobb角的处理需要将数组中的角度数据按正负号的变化放置到不同的子数组中,依次对数组中的角度数据进行排序,最后进行Cobb角计算。多Cobb角的计算以脊柱后凸为例,俯仰角的集合为θ={θ0,θ1,θ2,…,θn}。假设存在i个Cobb角则有i个正负号变化节点为θj={θj1,θj2,…,θji},那么集合θ将分成(i+1)个子集:

(12)

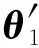
(13)

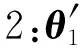
(14)

根据式(13)和式(14)可以计算出多个Cobb角的情况。

2 测量实验平台构建

2.1 硬件电路

脊柱测量仪的硬件结构主要由电源电路、脊柱棘突点姿态数据采集电路、编码器数据采集电路、显示电路和无线数据传输电路。设备系统中测量模块的姿态传感器用于采集患者脊柱棘突点的俯仰角和偏航角;编码器用于测量每两个数据采集位置间的距离,为脊柱曲线拟合提供位置信息[13-14];控制系统模块中的显示模块LCD用于显示每个采集点的俯仰角和偏航角并且显示最终的侧弯和后凸的Cobb角;无线模块主要用于主控模块和上位机的通讯,包括指令传输和数据传输。MCU判断开始测量按钮的状态开始测量,通过判断测量按钮的状态进行姿态传感器和编码器的数据采集,采集数据后MCU通过算法计算得出Cobb角,将Cobb角数据送到LCD屏幕显示,系统硬件组成如图5所示,组装后的设备如图6所示。

图5 测量设备硬件组成

图6 完整的脊柱测量仪

2.2 测量与数据处理

脊柱形态测量软件主要实现的功能有:①判断数据采集按钮的状态;②通过I2C通信方式采集姿态传感器的数据信息;③通过模拟SPI通信将脊柱点的姿态数据和处理后读出的Cobb角数据发送到屏幕显示;④外部中断的方式读取编码器的相位数据计算得出距离;⑤当数据传输开启后用串口将数据发送到蓝牙4.0模块,下位机的软件流程图如图7所示。

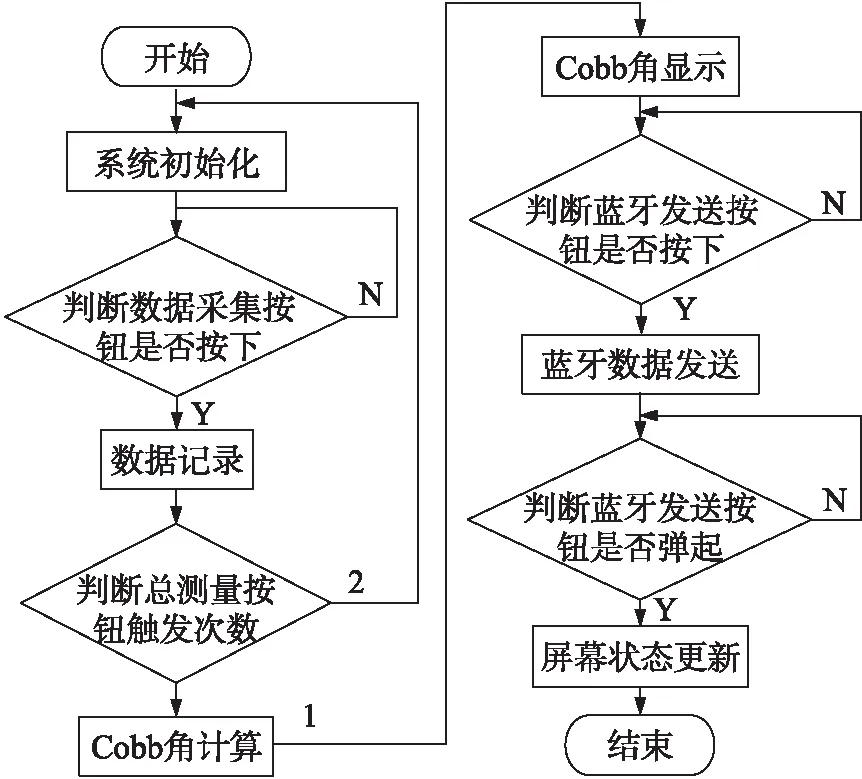
图7 软件流程图

编码器的应用原理:如果A相超前B相,那么编码器的旋转方向被认为是正向的,如果A相位落后于B相,编码器的旋转方向是反向的。AB相信号频率一致,相位相差90度。对编码器的测试采用外部中断检测,将A相输入接入到单片机的外部中断0口,设置上升沿触发中断,在中断程序中判断B相的电平,如果是B相为低电平,则正转计数,如果B相为高电平则反向计数。编码器软件流程图如图8所示。

图8 编码器软件流程图

3 实验验证

3.1 模拟脊柱形态曲线实验

模拟实验的目的是验证非X线脊柱形态测量仪的测量准确度和重复性。从人体的实际X线图像(如图9所示)看出,常见人体的基本脊柱畸形包括侧弯1个Cobb角和后凸2个Cobb角。为了模拟实验的效果,实验条件需要包括这3个Cobb角。

图9 脊柱X射线图

实验方法:首先设定标准的Cobb角,设定侧弯Cobb角为43.6°,后凸设定2个Cobb角分别为48°和49°,经过数学推导得出三维曲线公式为:

(15)

利用MATLAB画出三维曲线如图10(a)所示,从曲线的二维图像可以主观地观察到侧弯Cobb角如图10(b)所示和后凸Cobb角如图10(c)所示。

图10 表示模拟人体脊柱的三维曲线、后凸平面和侧凸平面

将三维曲线制作成实验模型,利用测量装置进行测量实验。将测量仪初始化,开始测量时将测量仪放置测量起始位,开始测量时沿着模拟脊柱线进行取点测量,测试过程进行到模拟脊柱线终点时结束,测量过程如图11所示。连续进行10次测量,记录每次测量的数据,包括侧弯Cobb角和后凸Cobb角,测量结果记录在表1中。

对实验数据进行处理,先求出每组Cobb角的算术平均值,算术平均值公式为:

(16)

图11 模拟实验测量过程

若n次的独立重复测量,得到的各次测量结果为Xi(i=1,2,…,n),那么其重复性s(Xi)可用贝赛尔公式计算:

(17)

对于精度的分析,采用标准差来判断,标准差的计算公式为:

(18)

对实验数据进行处理的结果如表2所示,由表中数据可知,使用仪器时对同一条曲线相同的测量人员的前提下,将10次人体脊柱形态测量仪测量的平均结果与理论计算的结果相比较,误差在±2°之内,误差范围在设计要求的±5°之内。

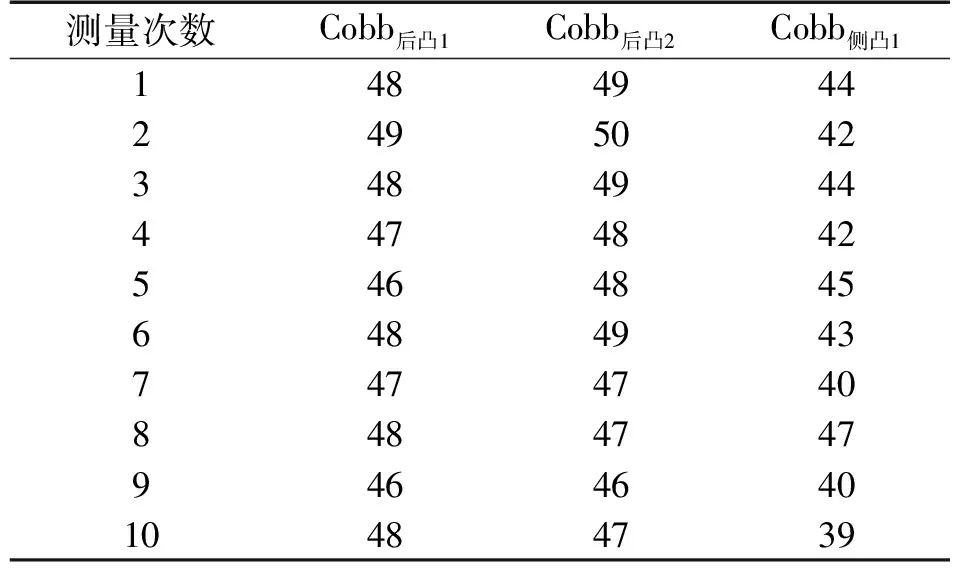
表1 模拟脊柱形态曲线实验数据测量结果

表2 模拟实验结果的处理

对于重复性的判断要求为:

s(Xi)<3σ

(19)

根据表中的计算结果都满足式(19)的条件,所以仪器的重复性满足测量需求。

3.2 医院实验

为了验证测量仪的可靠性,将测量仪在医院对脊柱畸形患者进行实验,实验过程为:对6位脊柱变形的患者进行实验,2个医生用测量仪进行数据采集测量,医生1对仪器初次接触,讲解过使用方法后开始测量,医生2已经可以熟练使用测量仪进行数据采集实验。对熟练使用测量仪的判断标准为:在模拟脊柱模型上的测量精度在±1°之内。每位医生对同一个患者进行3次测量实验,测量患者的侧弯Cobb角,测量结果记录在表3中。

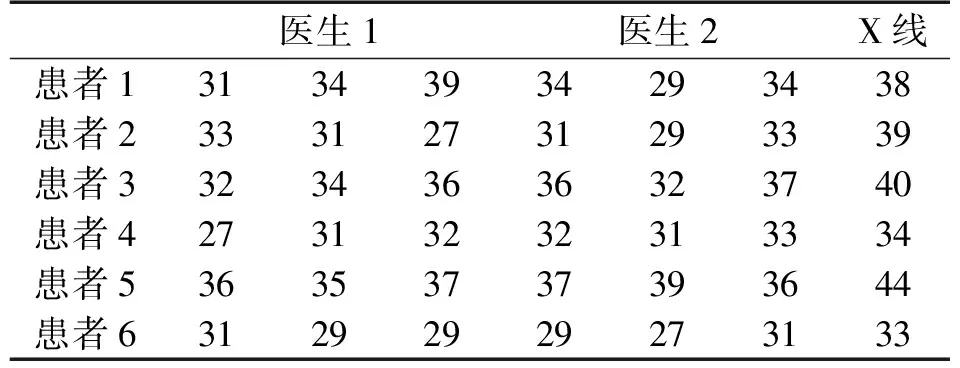
表3 医院实验数据

首先对医生1的数据结果进行分析,由于单个患者测量次数少,所以不进行重复性分析,分析结果如表4和表5所示。

表4 医生1的实验结果分析

实验结果表明:医生2大部分测量结果的误差值小于医生1的测量结果,医生2大部分测量结果的标准差也小于医生1的测量结果。

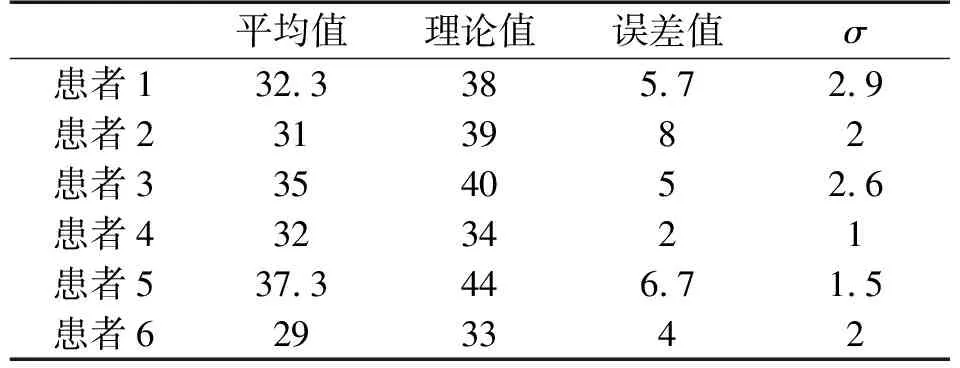
表5 医生2的实验结果分析

采用配对样本T检验去计算测量的相关性,首先将医生1和医生2的测量数据分别与X线的数据进行配对样本T检验,然后再进行医生1和医生2之间的配对样本T检验计算,计算结果如表6所示。

表6 配对样本T检验计算结果

由测量结果的分析,医生1和医生2的测量结果与X线的结果的相关系数均大于0.75,说明相关程度较好,医生2对于X线的相关系数高于医生2对于X线的相关系数。由分析可得出结论:测量技术的可靠性较好,测量技术的熟练程度会对实验结果产生正相关影响。

4 结论

本文研究了一种基于姿态传感器的非X线的脊柱形态测量技术,利用姿态传感器采集到的脊柱姿态信息通过算法运算得出Cobb角数据,为脊柱形态的测量提供了一种新的手段。基于姿态传感器的脊柱测量技术可以实时显示出测量的Cobb角,同时配合编码器的数据可以拟合出脊柱的三维形态。测量仪器经过实验表明具有较高的测量精度和测量重复性,能够方便地应用于患者的日常脊柱形态评估。

参考文献:

[1] 崔泰铭,陈胤,王健. 青少年特发性脊柱侧弯发病机理的研究进展[J]. 中国学校卫生,2007,28(9):856-859.

[2] Finestone A S,Marcus G,Anekstein Y,et al. Assessing Kyphosis with Spine Scan:Another Attempt to Reduce Our Dependence on Radiography.[J]. Spine Journal,2013,13(8):926-931.

[3] Ochia R S,Inoue N,Renner S M,et al. Three-DimensionalinvivoMeasurement of Lumbar Spine Segmental Motion[J]. Spine,2006,31(18):2073-2078.

[4] Nagamoto Y,Ishii T,Sakaura H,et al. In vivo Three Dimensional Kinematics of the Cervical Spine during Head Rotation in Patients with Cervical Spondylosis[J]. Spine(Phila Pa 1976),2011,36(10):778-783.

[5] Dvir Z,Prushansky T. Reproducibility and Instrument Validity of a New Ultrasonography-Based System for Measuring Cervical Spine Kinematics[J]. Clin Biomech,2000,15(9):658-664.

[6] Tousignant-Laflamme Y,Boutin N,Dion A M,et al. Reliability and Criterion Validity of Two Applications of the iPhone to Measure Cervical Range of Motion in Healthy Participants[J]. J Neuroeng Rehabil,2013,10(1):69.

[7] Padulo J,Ardigò L P. Vertebral Rotation in Adolescent Idiopathic Scoliosis Calculated by Radiograph and Back Surface Analysis-Based Methods:Correlation between the Raimondi Method and Rasterstereography. Eur Spine J;22:2336-2337[J]. European Spine Journal,2014,23(4):922-923.

[8] Lee R Y W,Laprade J,Fung E H K. A Real-Time Gyroscopic System for Three-Dimensional Measurement of Lumbar Spine Motion[J]. Medical Engineering and Physics,2003,25(10):817-824.

[9] Quek J,Brauer S G,Treleaven J,et al. Validity and Intra-Rater Reliability of an Android Phone Application to Measure Cervical Range-of-Motion[J]. Journal of Neuroengineering and Rehabilitation,2014,11(1):65.

[10] Heuer F,Schmidt H,Claes L,et al. A New Laser Scanning Technique for Imaging Intervertebral Disc Displacement and Its Application to Modeling Nucleotomy[J]. Clin Biomech(Bristol,Avon),2008,23(3):260-269.

[11] 孙伟,闫慧芳,李瑞豹,等. 基于惯性技术的端帮采煤机姿态测量仪设计[J]. 传感技术学报,2016,29(2):306-312.

[12] Cretella M A,Duggineni V M,Eng M C,et al. Sensor Fusion:US,US8624695[P]. 2014.

[13] 陈建军,沈林勇,钱晋武,等. 已知离散点曲率的曲线拟合递推方法[J]. 上海大学学报(自然科学版),2003,9(2):123-126.

[14] 邱亚,沈林勇,胡卫建,等. 缝隙搜救机器人镜体的形状重建和定位方法[J]. 仪器仪表学报,2015,36(12):2782-2789.