基于细芯光纤与双球结构的干涉型光纤传感器*

李德强,曹 晔*,宫顺顺,辛鹏程,孙朝阳,杨长龙,李丽君

(1.青岛大学电子信息学院,山东 青岛 266071;2.山东科技大学电子通信与物理学院,山东 青岛 266590)

21世纪初中国步入信息化时代,快速发展的信息化时代对信息的采集的准确性和高精度有了进一步的要求,研究新型的光纤传感器,来满足信息化时代的需求是信息通信领域的一大变革。近几年,越来越多的科研工作者研究干涉型光纤传感器,并把研究成果应用于航天、医疗、环境监测、通信等诸多领域[1-6],取得了良好的经济效益和突出的成绩。干涉型光纤传感器可以由球形[7-8]、花生锥形[9]、拉锥[10]和错芯[11]等结构构成,目前可以实现对温度、折射率、应变、磁场等物理量的测量。例如2014年,傅海威等设计了一种基于单模-多模-细芯-单模光纤的马赫-曾德尔(MZ)干涉结构,测得干涉谷的折射率和温度的灵敏度分别是为-53.03 nm/RIU和0.046 5 nm/℃[12]。2015年,WuJixuan等提出了一种基于细芯光纤(TCF)的光纤传感器,并进行了位移和温度的双参量同时测量,位移的灵敏度达到了-0.010 28 nm/μm 和-0.015 35 nm/μm,温度的灵敏度达到了0.009 42 nm/℃ 和0.004 93 nm/℃[13]。2016年,梁明玉等提出一种基于马赫-曾德尔干涉的球形结构光纤温度传感器,测得中间单模光纤为1.8 cm时的温度灵敏度为0.129 7 nm/℃[14]。2016年,周孟晖等制作了基于细芯光纤的MZ干涉传感器,实现了对温度、折射率、应变、弯曲的测量,灵敏度分别为72.0 nm/℃、-8.12 nm/RIU、1.8 pm/μm、2.07 nm/m-1[15]。

本文设计制作了一种基于细芯光纤和双球结构的干涉型光纤传感器,利用纤芯模式与包层模式的干涉,实现了对温度、折射率和拉力的测量,该传感器有较好的灵敏度和线性度。

1 传感原理

本文制作了一种球形-细芯-球形干涉型光纤传感器。在两根单模光纤上分别做出球形结构,与细芯光纤熔接,制作成的传感结构如图 1所示。

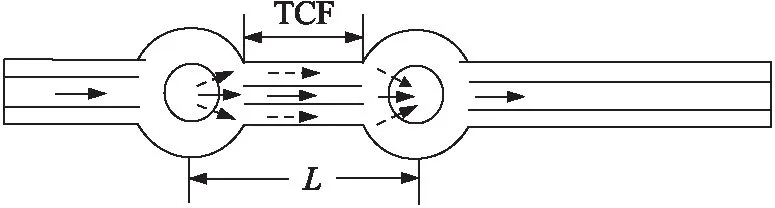
图1 光纤传感器结构示意图

入射光通过单模光纤进入左端的球形结构,由于球形结构的耦合作用,一部分光进入细芯光纤的纤芯,另外一部分耦合进入包层,分别激发出细芯光纤的纤芯模式与包层模式,这两种模式传输到右端的球形结构时发生耦合,包层模式会耦合回单模光纤的纤芯。由于传输路径不同,纤芯模式和包层模式之间存在相位差,从而形成干涉。该干涉是基于马赫曾尔德(M-Z)干涉理论,因此该传感器是基于M-Z干涉的光纤传感器。纤芯模式与包层模式的相位差表达式为[16]:

(1)

式中:L为干涉长度,λ为真空中的波长,Δneff=nco-ncl是纤芯与包层有效折射率的差,nco是纤芯有效折射率,ncl是包层有效折射率,nex是外界折射率。

干涉时光的光强表达式[17]为:

(2)

式中:I1与I2分别为细芯光纤的纤芯模和包层模的光强。

当φ=(2m+1)π(m为正整数)时,干涉光强达最小值,出现干涉谷。由表达式(1)得波谷的波长为:

(3)

当温度变化时,纤芯与包层有效折射率之差与干涉长度L会发生变化,从而引起干涉谷漂移。当外界环境折射率变化时,会引起包层模式的有效折射率变化,从而引起干涉谷漂移。当光纤受到拉力时,光纤的长度和有效折射率都会发生变化,从而使得干涉谷漂移。所以,从理论上分析,该传感器可以实现对温度、折射率和拉力这3个物理量的传感。

2 实验结果和分析

2.1 传感结构的制作

调节熔接机放电强度为200 bit,放电时间为 1 300 ms,在两根单模光纤上分别制作球形结构,如图2所示。调节放电强度为100 bit,放电时间为1 300 ms,将两个球与2 cm小芯径熔接在一起,制作出传感器。实验中用的熔接机是古河FITEL-S177。细芯光纤用的是长飞公司生产的,其包层直径为125 μm,在1 550 nm的中心波处的模场直径约4.5 μm,纤芯和包层的有效折射率分别是1.445 7是1.437 8。单模光纤包层直径为125 nm,纤芯直径为9 nm。实验中用的光谱仪(OSA)为横河的YOKOGAWA-AQ6370,精度为0.01 nm。

图2 显微镜下双球结构示意图

2.2 温度特性实验

将双球结构水平拉直固定在恒温水浴箱TCC(Temperature Controlled Container)内,如图 3所示,图3中BBS为宽带光源,OSA为光谱仪。保证不受水压、弯曲、拉力等外界因素的影响,从35 ℃至90 ℃不断增加恒温水浴箱的温度,每5 ℃取样一次,记录光谱仪上干涉谷的波长。

图3 温度特性实验装置图

实验结果如图4、图5所示,随着水温的升高,光谱仪中显示波形右移,与理论分析相符。图4中Dip1在35 ℃时的波长为1 541.433 3 nm,90 ℃时的波长为1 547.100 0 nm。通过数据拟合,此干涉型传感器的温度灵敏度为0.066 5 nm/℃,线性度为0.982,如图 5所示。随着温度的升高,热光效应使有效折射率差增大,热膨胀效应使干涉长度L增大,由式(3)可知,波谷将向长波方向漂移。图4中透射谱随着温度升高向长波方向移动,与理论分析相符。

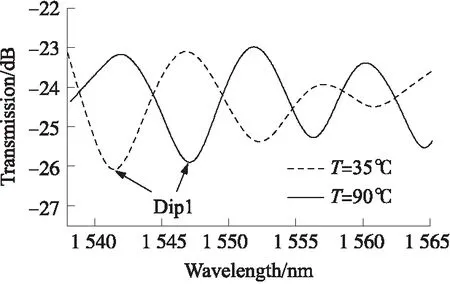
图4 干涉谷随温度漂移的透射谱

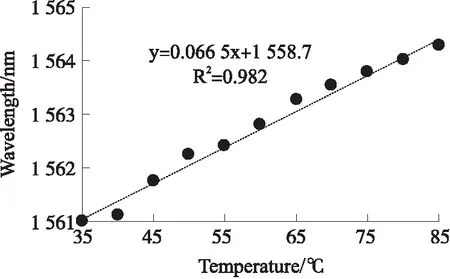
图5 温度灵敏度响应曲线

本实验采用水浴加热,如果采用其他加热方式,将进一步提高测量范围。

2.3 折射率特性实验

用精准电子秤和量筒配置浓度分别是0.1、1、3、5、7、9、11、13、15、17、19、21、23、25的盐溶液,溶液浓度与折射率的对应关系如表1所示。

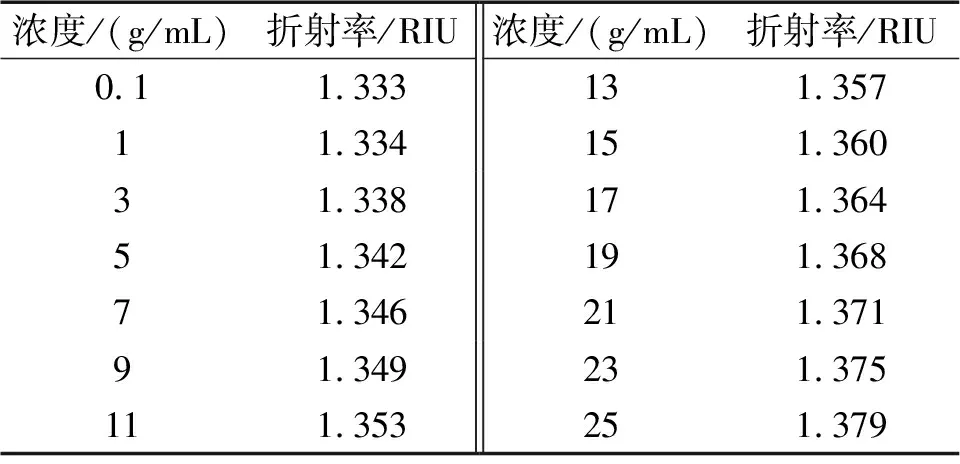
表1 溶液浓度与折射率的对应关系

将传感结构水平拉直固定在折射率槽RIS(Refractive Index Slot)内,如图 6所示,保证不受温度、拉力、弯曲等外界因素的影响。在折射率槽中依次加入不同折射率(从1.333到1.379)的盐溶液。更换溶液时,先将盐溶液用针管吸出,用清水重复清洗晾干后,再注入新的盐溶液。记录下光谱仪上干涉谷的波长。

图6 折射率特性实验装置图

实验中,随着外界环境的折射率增大,包层模式的有效折射率变化,从而使干涉谷左移,如图 7所示。图7中Dip2在折射率为1.333和1.379的波长分别是1 551.633 3 nm和1 550 nm。通过数据拟合,该结构的折射率灵敏度大小为-33.652 nm/RIU,线性度为0.979 2,如图8所示。随着溶液折射率的增大,包层模式的有效折射率变化,从而使有效折射率差减小,由式(3)可知,波谷将向短波方向漂移。图7中透射谱随折射率增大向短波方向移动,与理论分析相符。

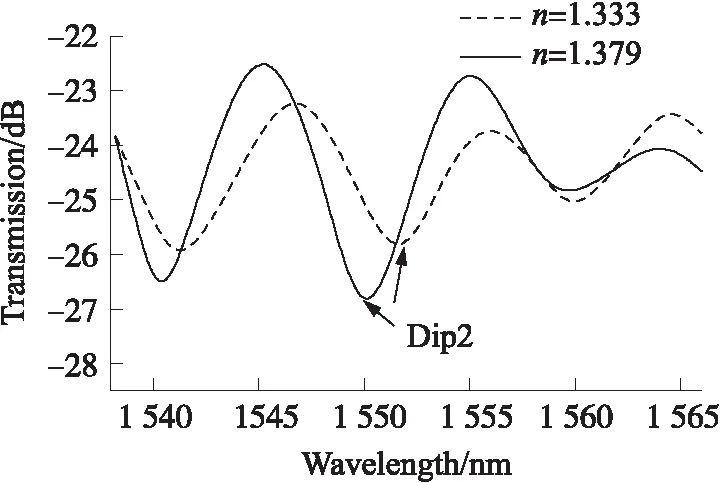
图7 干涉峰随折射率漂移的透射谱

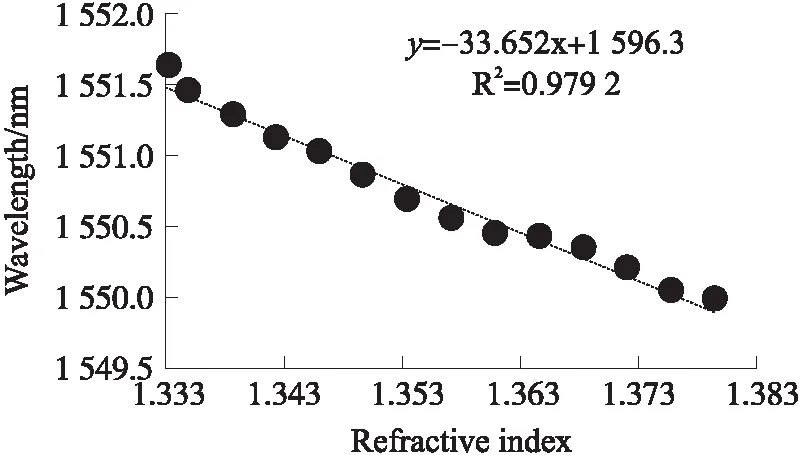
图8 折射率灵敏响应曲线

2.4 应变特性实验

如图9所示,将传感头拉直粘贴在悬臂梁上,在悬臂梁的自由端悬挂砝码时,悬臂梁产生弯曲,带动传感头形变。在悬臂梁的自由端增加砝码,从100 g增大到1 000 g,每增加100 g记录一次数据。

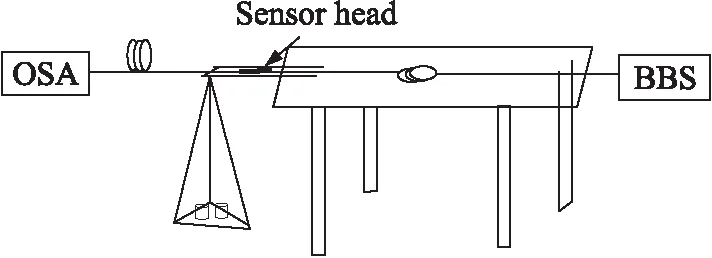
图9 拉力特性实验装置图

图10 干涉峰随拉力变化的透射谱

实验中,随着重物质量的不断增加,光纤发生形变,有效折射率变化,干涉谷左移,如图10所示。

图10 中Dip3在拉力为0.98 N和9.8 N时,波长分别为1 540.400 0 nm和1 536.833 3 nm。通过数据拟合,拉力的灵敏度大小为-0.360 8 nm/N,线性度为0.965 1,如图11所示。随着拉力的增加,悬臂梁带动传感器产生应变,随着拉力的增大,应变也增大。弹光效应使有效折射率差减小,是主要因素;应变使干涉长度L增大,是次要因素。由式(3)可知,波谷将向短波方向漂移。图10中透射谱随拉力增大向短波方向移动,与理论分析相符。

如果改进悬臂梁实验条件,会进一步增加测量范围,该传感结构在安全监测等领域有广泛的应用。

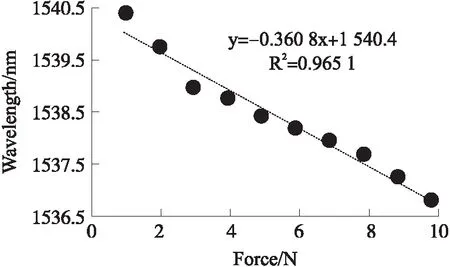
图11 拉力灵敏度响应曲线

3 结论

本文实验在两根单模上制作球形结构,并在中间熔接细芯光纤形成MZ干涉结构。利用该结构对温度、折射率和拉力进行了测量,实验结果表明,此结构对温度、折射率、拉力都灵敏,温度灵敏度、折射率灵敏度、拉力灵敏度分别为0.066 5 nm/℃、-33.652 nm/RIU、-0.360 8 nm/N,且线性度良好。

参考文献:

[1] Esmaeil Mobini,Arash Mafi. Design of a Wavelength-Tunable Optical Tweezer Using a Graded-Index Multimode Optical Fiber[J]. Journal of Lightwave Technology,2017,35(18):3854-3861.

[2] Wo Jianghai,Sun Qizhen,Liu Hai,et al. Sensitivity-Enhanced Fiber Optic Temperature Sensor with Strain Response Suppression[J]. Optical Fiber Technology,2013,19(4):289-292.

[3] Zhao Yong,Zhou Xue,Li Xuegang,et al. Review on the Graphene Based Optical Fiber Chemical and Biological Sensors[J]. Sensors and Actuators,B:Chemical,2016,231:324-340.

[4] Hu Haifeng,Sun Sijia,Lü Riqing,et al. Design and Experiment of an Optical Fiber Micro Bend Sensor for Respiration Monitoring[J]. Sensors and Actuators,A:Physical,2016,251:126-133.

[5] Xiao Hengli,CuiXinlin,LeiWenkai. A Bored Pile Deficiency Detection Method Based on Optical Fiber Temperature Measurement[J]. Optical Fiber Technology,2015,21:1-6.

[6] 邵靖,段力,王强,等. MEMS高温温度传感器的研制与测量精度研究[J]. 传感技术学报,2017,30(9):1352-1358.

[7] 曹晔,赵晨,童峥嵘. 可双参量同时测量的干涉型全光纤传感器[J]. 光子学报,2015,44(10):1006102.

[8] Zhang Jun,Gong Huaping,Wang Zhiping,et al. M-Z Optical Fiber Liquid Level Sensor Based on Two Cascaded Spherical-Shape Structures[C]//ICOCN 2016,2016:7875662.

[9] Gong Huaping,YangXiao,Ni Kai,et al. An Optical Fiber Curvature Sensor Based on Two Peanut-Shape Structures Modal Interferometer[J]. IEEE Photonics Technol Lett,2014,26(1):22-24.

[10] Musa B,Roze A A,Noor A S M,et al. Effect of Fiber Profile Parameters on the Transmission Properties of the Tapered Optical Fibers[C]//Conf Proc—IEEE Int Conf Photonics,ICP,2011:6106862.

[11] 曹晔,刘文,赵舜,等. 基于光子晶体光纤和单模光纤错芯结构的光纤传感器[J]. 光电子·激光,2015,26(07):1233-1237.

[12] 傅海威,闫旭,李辉栋,等. 基于纤芯失配型马赫曾德尔光纤折射率和温度同时测量传感器的研究[J]. 光学学报,2014,34(11):66-71.

[13] Wang Jixuan,Miao Yinping,Song Binbin,et all.Simultaneous Measurement of Displacement and Temperature Based on Thin-Core Fiber Modal Interferometer[J]. Optics Communications,2015,340:136-140.

[14] 梁明玉,郎婷婷,金嘉俊,等. 基于马赫-曾德尔干涉的球形结构光纤温度传感器[J]. 光电子·激光,2016,27(12):1255-1259.

[15] 周孟晖,董新永,杨菁怡,等. 细芯光纤M-Z干涉传感器多参数测量研究[J]. 光电子·激光,2016,27(06):587-592.

[16] Gu Ningning,Zhang Hao,Liu Bo,et al. Magnetic Field Sensor Based on Concatenation of Fiber Peanutand Long-Period Fiber Grating with Resolved Temperature Cross Sensitivity[C]//ICOCN,2016:7875663.

[17] 吴浩伟,应朝福,彭保进,等. 基于薄芯光纤模态干涉技术的折射率传感特性实验研究[J]. 光子学报,2011,40(12):1881-1883.