低位截断瑞利噪声的统计推理

李增辉, 李建勋, 李光伟, 王恩堂

(1. 空军研究院, 北京 100085; 2. 中国人民解放军93498部队, 河北 石家庄 050071)

0 引 言

预警雷达担负着国土防空、航空管制、引导攻击、目标指示以及远程战略预警等重要任务，是平时和战时的重要武器装备[1]。随着电子技术的演进，干扰与反干扰技术之间的斗争愈演愈烈。

在复杂电磁环境下，为了保持雷达效能和提高生存能力，只有不断提升抗干扰性能，降低干扰对雷达性能的影响[2-4]。同时，通过构建复杂电磁环境，评估预警雷达抗干扰性能对于预估战时雷达实际效能具有重要意义[5-7]。

预警雷达抗噪声压制干扰能力评估常需要对通道噪声幅度的均值进行估计。从理论上说,在脉冲压缩体制的雷达系统中,脉冲压缩后的噪声通常服从瑞利分布,因此对通道噪声幅度均值的估计本质上是对服从瑞利分布的噪声进行统计推理。关于瑞利分布的统计估计已有大量研究[8-14]。然而,雷达系统在处理过程中,通常会对噪声进行量化处理,受采样位数影响还可能舍弃低位数据。如果仍然采用瑞利分布下的噪声估计方法,必然导致一定的估计偏差,尤其是量化电平较高或者低位舍弃位数较多的情况。

为了对截断量化后的瑞利噪声样本进行有效的统计推理,降低估计偏差,本文从瑞利分布和多项分布出发,推导得到了瑞利分布参数的极大似然估计、无信息先验贝叶斯估计和共轭先验贝叶斯估计方法,仿真实验验证了所提算法的有效性。

1 噪声样本统计估计模型

1.1 低位截断的瑞利分布样本的统计分布

设xi(i=1,2,…,n)为服从瑞利分布的样本,即[15]

p(x;λ)=2λxexp(-λx2)

(1)

式中,参数λ与样本均值和方差的关系为

(2)

(3)

(4)

式中,参数向量θ=[θ0,θ1,…,θK-1]中的参数θk为噪声样本量化截断后取的k概率,且

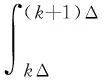
e-λk2Δ2{1-exp(-λ(2k+1)Δ2)}

(5)

同时θK为噪声样本量化截断后取值大于K的概率,且

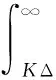
(6)

从而,在给定量化截断后样本时,参数λ的对数似然函数为

lnL(λ|n)=lnp(n;θ)=

(7)

式中,参数θk按照式(5)取值。

1.2 最大似然估计及其凸优化

根据式(7)给出参数λ的最大似然估计公式为

ln[1-exp(-λ(2k+1)Δ2)]}

(8)

求对数似然函数ln L的二阶导数可得

(9)

即对数似然函数为凸函数,因此理论上以大于零的任意实数为初值进行迭代寻优总能找到式(8)中优化问题的全局最优解,即解得最大似然估计。

事实上,截断后的瑞利样本的均值以很大的概率满足

(10)

因此,取式(10)中λ的上限为初值,可使优化问题快速收敛到最优解,即使式(10)以极小概率不成立时,也不会影响问题的收敛性。

1.3 贝叶斯估计

由于超参数λ的似然函数无法简单分离样本统计量,相应的共轭先验分布也无法直接给出。因此,贝叶斯估计中采用瑞利分布的共轭先验分布来近似超参数λ的共轭先验,即Gamma分布[16]

(11)

其中,α>1，β>0,则后验分布可得

π(λ|n)=π(λ;α,β)L(λ|n)∝

exp{-βλ+(α-1)lnλ+lnL(λ|n)}

(12)

对式(12)取对数并求二阶导数可得

(13)

因此,超参数λ的后验分布为对数凹分布,可以采用[17]中对于对数凹分布产生随机数的方法生成足够多的随机样本,进而采用求样本均值的方法实现超参数的精确后验估计。

设生成服从后验分布的随机样本为λi(i=1,2,…,N),则超参数λ的后验期望估计为

(14)

后验方差为

(15)

区间估计下限估计为

⟹

(16)

(17)

当没有先验信息可用时,需要引入无信息先验或弱信息先验分布。比如引入无信息先验分布

π(λ)∝1

(18)

时,相当于式(12)中的后验分布退化为似然函数形式,此时后验分布的二阶导数仍然小于零,即式(13)中的参数α取1时的情况,也就是后验分布仍然为对数凹分布,依然可以采用上述方法生成随机样本。因此,在共轭先验分布条件下给出的后验期望、后验方差和区间估计公式对无信息先验分布同样适用。

此外,在引入无信息先验条件下,生成超参数后验分布的随机样本后,可以根据超参数的先验分布对先验分布的参数α和β进行最大似然估计[18]

(19)

式中,校正因子μ=(N-1)/(N+2)。

2 仿真数据处理与分析

为了方便实验分析,不妨设量化间隔Δ取值为1。取参数λ的真值为1,即α=β,在取不同α和β参数值情况下,先验分布如图1所示,显然取值越大,分布越集中,这也意味着引入的先验信息越多。

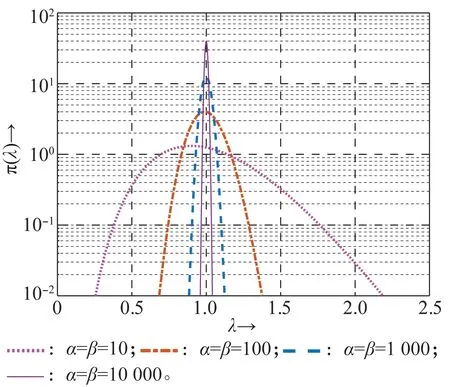
图1 不同参数下的先验分布Fig.1 Prior distributions under different parameter values

生成50个服从瑞利分布的随机样本,在量化截断后取值情况如表1所示,量化后的数值仅包含0、1、2共3种数值。

表1 截断量化后瑞利噪声取值情况

如果将量化后样本仍然按照瑞利分布来估计参数数值,那么按照式(2)估计参数λ可得

(20)

显然,估计值远离真值1。相比之下,如图2所示,极大似然估计为0.972,无信息先验条件下的贝叶斯估计为1.003,后验方差为0.03,后验区间估计为[0.49,1.95],估计结果均远优于式(20)的估计值。需要说明的是,极大似然估计的偏差并不是优化误差,而是极大似然函数本身存在的偏差,这也说明引入先验分布进一步修正似然函数曲线的必要性。

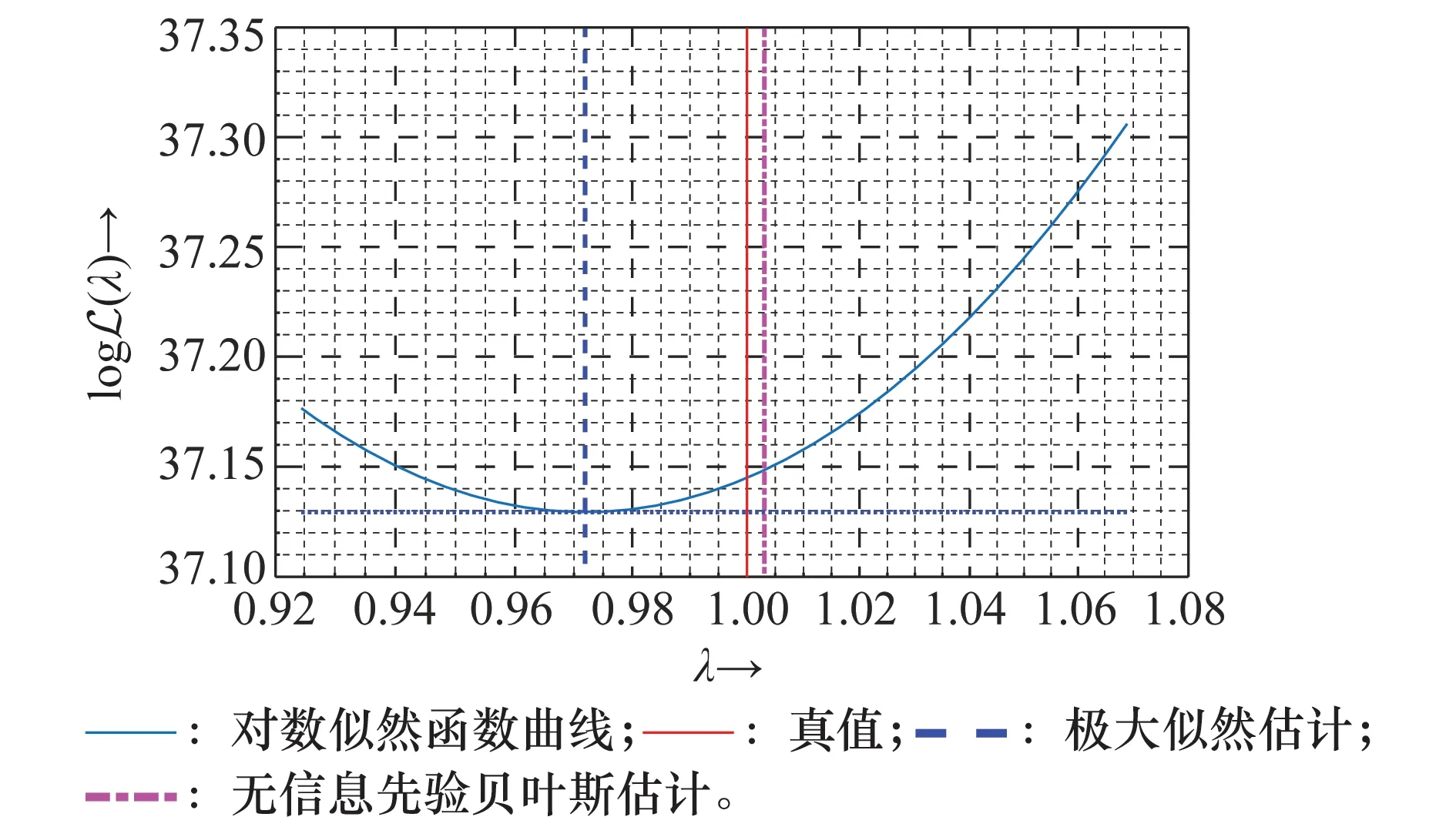
图2 对数似然函数曲线与估计结果Fig.2 Logarithm likelihood function curves and the associated estimates

虽然量化截断后的瑞利分布参数的共轭分布不是Gamma分布,但从图3来看,一方面按照对数凹分布生成的随机样本与后验分布符合较好;另一方面,后验分布与Gamma分布非常接近,在一定程度上说明采用Gamma分布作为先验分布的合理性。

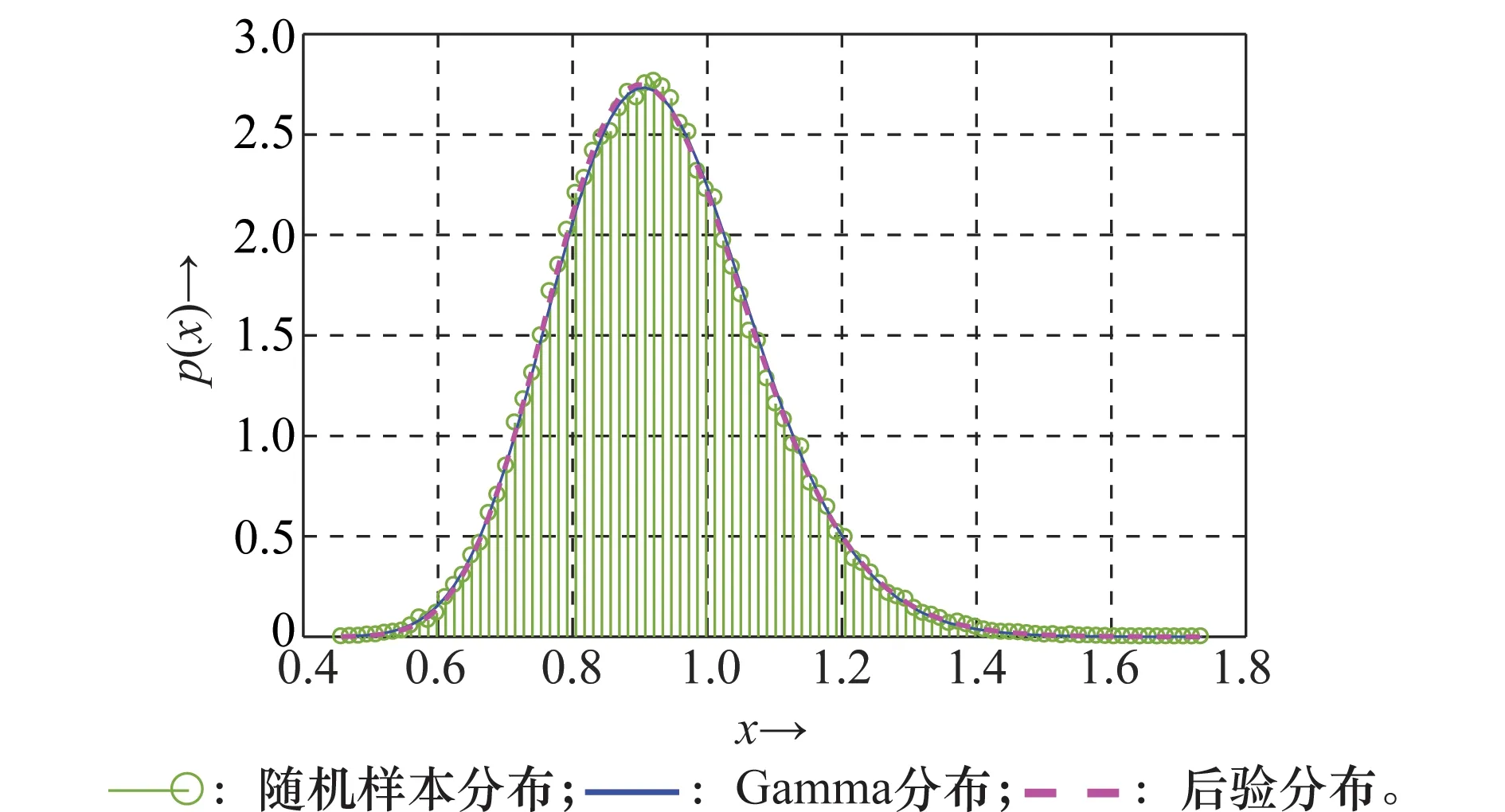
图3 服从后验分布的随机样本分布Fig.3 Histogram of the posterior distributed samples

在无信息先验条件下,贝叶斯估计不仅可以给出后验期望,同时还可以给出共轭先验分布参数的估计值。使用上述50个随机样本可以估计出先验分布参数,相应的分布曲线如图4所示。

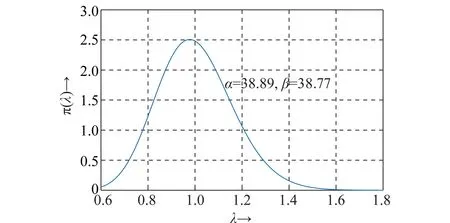
图4 无信息先验条件下的先验分布估计Fig.4 Parameter estimation of the noninformative prior distribution

在共轭先验分布参数估计的基础上,进一步生成50个随机样本,并执行1 000次蒙特卡罗分析,可得极大似然估计、无信息先验贝叶斯估计和共轭先验贝叶斯估计结果的分布情况,如图5所示。

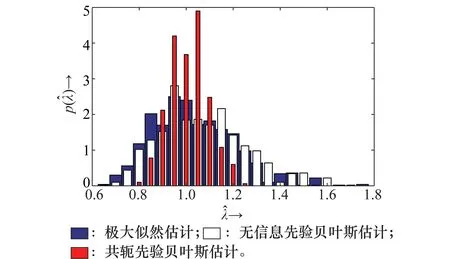
图5 不同估计方法1 000次估计值的分布直方图Fig.5 Histograms of 1 000 estimates with different estimation algorithms

从实验结果看,与极大似然估计相比,无信息先验贝叶斯估计性能改善不明显,这主要是引入的先验本质上并未增加信息的缘故,同时,无信息先验贝叶斯估计是利用参数分布求解的参数的后验期望估计,极大似然估计是求解使参数分布最大的参数得到的,前者更为充分的运用的样本数据,因此性能略有改善。而共轭先验贝叶斯估计由于引入了有效的先验信息,使得估计结果更集中于真值附近,即在先验分布的作用下降低了估计方差。

3 结 论

本文针对截断量化瑞利噪声的估计问题,推导了噪声的统计分布,通过证明极大似然函数的凸函数性质和贝叶斯后验分布的对数凹分布性质,提出了极大似然和贝叶斯估计方法。通过设计仿真实验，利用生成的截断量化后瑞利噪声样本进行统计推理，不仅验证了所提统计估计算法的有效性,还直观反映了引入先验信息对参数估计精度的影响。