考虑预测响应值波动的多响应优化设计

汪建均, 屠雅楠

(南京理工大学经济管理学院, 江苏 南京 210094)

0 引 言

近年来,随着产品设计的复杂化以及顾客需求层次的多样化,在产品或工艺过程的优化设计中往往需要同时考虑多个质量特性,因此多响应优化设计在持续性质量改进活动中显示出越来越重要的地位和作用[1]。多响应优化设计旨在寻求一组最佳的参数设计值,使多个质量特性能够同时达到最优的设计值。然而,在多响应优化设计的建模过程中,往往无法准确估计模型的回归系数。如果忽略模型参数的这种不确定性,试验结果将会产生误差,甚至得出不科学的结果[2]。此外,在产品的生产过程中,存在多种噪声因子的干扰,这些噪声因子会对质量特性的输出结果造成很大影响,使得预测响应值存在较大的波动,导致试验结果难以有效地复现[3]。

目前解决多响应优化设计问题的主要方法有以下几种:满意度函数法、马氏距离法、多元质量损失函数方法、贝叶斯后验概率法等[4]。满意度函数法最早是由文献[5]在1965年提出的,经过众多质量学者的不断改进和完善,形成了一系列改进的满意度函数。其中,最常用的一种是由文献[6]所提出的综合满意度函数。该满意度函数法操作简单、易于理解,是使用最广泛的多响应优化设计方法。然而,传统的满意度函数往往忽略了响应之间的相关性以及噪声因子对优化结果的影响[7],对响应的预测效果以及优化结果的可靠性考虑较少[8-9]。在这种情况下,通过上述满意度函数法所得到的优化结果往往是不可靠的,甚至会产生错误的结果。文献[10]提出了一种指数满意度函数,利用拟合优度提高了优化结果的可靠性,同时通过调节满意度函数的形状考虑了模型的预测能力。但是,该方法没有考虑响应之间的相关性。文献[11]提出一种改进的双指数满意度函数,该方法引入了质量损失函数来考虑响应间的相关性。但是,该方法也存在一些不足,未考察响应的预测误差,同时响应的质量损失难以有效确定。文献[12]提出一种改进的满意度函数法,其主要优势在于将双响应曲面方法引入到满意度函数中,能够有效解决均值响应与方差响应之间的相关性问题。文献[7]提出了改进的满意度函数模型,该方法同时将可控因子和噪声因子引入到满意度函数,考虑了噪声因子对多响应优化结果的影响。马氏距离方法作为多响应优化设计的一种常用方法,也引起广大质量学者的广泛关注和重视。例如,文献[13]提出的马氏距离只考虑了响应的方差-协方差结构,未考察各个响应的相对重要性。为此,文献[14]提出了加权马氏距离,使优化结果具有一定的可靠性。该方法既考虑了响应的方差-协方差结构,还考虑了各个响应在经济上的相对重要性。但是,该方法中的相对重要性受主观因素的影响。如果权重设置不合理,该方法的优化效果会受到较大的影响。此外,马氏距离方法主要是通过响应之间的方差-协方差结构来考虑多响应之间的相关性,但是通常忽视了响应的预测能力和优化结果的可靠性。多元质量损失函数也是目前最为常用的多响应优化设计方法之一,也引起众多质量研究者的广泛兴趣。例如,文献[15]提出的多元损失函数,考虑了过程的经济性和响应间的相关性。然而,该方法存在较大的局限性,仅仅适合解决望目质量特性的问题。为此,文献[16]扩展了文献[15]的研究工作,将该方法的适用范围扩大到望大质量特性和望小质量特性问题。文献[17]提出的多元质量损失函数,考虑了响应的预测能力,但是忽略了响应之间的相关性。因此,文献[18]结合文献[15]和文献[17]提出的两种方法,构建了新的多元质量损失函数,该方法能够同时考虑响应之间的相关性以及响应的预测能力。但是,该方法仍然存在缺陷,最主要的问题是无法评估优化结果的可靠性。文献[19]提出一种新的质量损失函数,该方法能够合理测算响应偏离目标值的程度。文献[20]提出一种加权的质量损失函数,该方法同时考虑了二次损失的期望和方差。文献[21]提出一种动态多响应稳健优化模型,该模型将多元偏正态分布和响应曲面法结合起来,建立了基于多元偏正态分布的期望损失函数,最后利用遗传算法进行优化求解。随着生产工艺复杂程度的日益提高,整个生产过程存在各种不确定性因素,尽管上述模型的理论基础很完善,但是在各自的建模过程中没有考虑模型参数不确定性和噪声因子的共同影响,这些因素将使得预测响应值产生较大的波动,因此上述模型难以精确地描述整个生产过程。

针对上述问题,一些学者提出了各自的研究方法。文献[22]提出,如果在建模过程中忽视模型参数的不确定性,该模型可能无法得到合理的优化结果。文献[23]提出了一种贝叶斯后验概率方法,该方法既考虑了过程分布的变化、试验数据间的相关性,同时还考虑了模型参数的不确定性,然后通过蒙特卡罗模拟方法计算多个响应的后验抽样值落在规格限内的概率。文献[24]考察了模型参数存在不确定性的多响应优化问题,结合贝叶斯方法开展研究工作。文献[25]将帕累托最优策略引入多响应优化设计,该方法考虑了模型参数的不确定性问题,其主要特点在于能够有效地利用图形展示这种不确定性对多响应优化结果和用户决策的影响。文献[9]提出利用置信区间优化多响应问题,当模型参数存在不确定性时,该方法能够给出更为合理的优化结果。文献[2]提出一种基于置信区间的多元质量特性满意参数设计方法,该方法考虑了模型参数不确定性的影响,利用双响应曲面模型和置信区间求解满足约束的相容性解集。文献[26]提出一种新的损失函数方法,该方法不仅考虑了模型参数的不确定性,还引入了试验过程中存在的实施误差,并通过实例证明该方法能够提高优化结果的稳健性和可靠性。另外,实际生产过程中存在各种噪声因子,这些噪声因子使得实际的生产过程难以通过单一的响应模型进行精确的刻画。正如著名的统计学家Box所说的那样“所有的模型都是错误,但是有些模型是有用的”。因此,一些研究人员开始关注如何通过组合建模方法以减少模型不确定性对优化结果的影响。例如,文献[27]提出一种基于模型不确定性的响应曲面建模方法,该方法将包容性检验引入组合建模方法中,以解决模型不确定性问题。文献[28]构建了一种新的损失函数,该方法结合位置和散度参数进行建模,并考虑了模型不确定性对试验结果的影响。文献[29]利用贝叶斯先验信息,评估预测响应的后验分布,该方法考虑了建模过程中可能存在的各种噪声因子对优化结果的影响。文献[30]通过置信区间衡量预测响应波动对优化结果的影响,该方法从置信区间端点选取最优值作为响应预测值,并利用图形显示预测响应波动的情况下优化结果的变化。文献[31]提出一种基于贝叶斯方法的递阶优化算法,该方法利用满意度函数求解初始解,再根据贝叶斯方法分析解的稳健性,综合考虑了过程波动(可控因子波动或存在噪声因子)和各种误差的影响。文献[32]结合质量损失函数和贝叶斯后验概率方法提出了一种新的多响应优化方法。该方法在多响应优化设计中同时考虑多响应之间的相关性、模型参数的不确定性以及优化结果的可靠性。然而,上述方法未能进一步考虑噪声因素以及模型参数的不确定性所导致的响应预测值波动对优化结果的影响,即不同研究方法所获得的优化结果在试验可重复性上的差异。在多响应优化设计中,如果忽略模型参数的不确定性,将难以精确地获得生产过程输入与输出的函数关系,从而无法确定最佳参数值;如果忽略噪声因子的影响,将会导致优化结果具有偶然性,甚至出现较大的偏差。然而,如何同时考虑模型参数的不确定性以及生产过程的噪声因子导致的预测响应值波动问题,目前可行的研究方法还不多。

因此,针对上述的问题,本文基于统一的贝叶斯多元回归模型框架,首先,通过蒙特卡罗模拟抽样得到各个响应的后验抽样值;然后根据帕累托最优原则计算帕累托最优前沿,并获得相应的多目标优化解集;最后,运用灰色关联分析方法对多目标优化解集进行关联度分析,选择关联度最大的作为理想的参数设计值。

1 基于贝叶斯多元回归模型的帕累托最优前沿

1.1 贝叶斯多元回归模型

在多响应优化设计中,假设有p个响应和q个因子效应,则多响应曲面回归模型为

y=Bz(x)+e

(1)

式中,y为p×1的响应矩阵;B为p×q的回归系数矩阵;z(x)为q×1的因子效应矩阵;e为p×1的随机误差矩阵,并且服从均值向量为0、方差-协方差矩阵为Σ的正态分布。

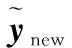
(2)

式中

(3)

(4)

(5)

(6)

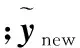
(7)

1.2 利用贝叶斯后验样本的帕累托最优前沿

在数学上,一个多响应优化问题[35]可表示为

S={x|h(x)=0;g(x)≤0}

(8)

式中,h(x)为等式约束;g(x)为不等式约束;S为定义域集合。

目前,针对多响应优化问题,普遍接受的一种解释是帕累托最优概念,即多响应优化问题不是为了求解某个唯一的最优解,而是针对响应之间的冲突关系给出一组折中解。而每一个折中解在目标空间中都对应着一个帕累托最优前沿点,这些前沿点的集合构成了帕累托最优前沿解集[30]。另外,在这个解集中,所有的点都具有帕累托最优性。

一个点x*具有帕累托最优性,即不存在这样的点x∈S,对于所有的r∈{1,2,…,n},都有fr(x)≤fr(x*),且至少有一个为严格不等式[36]。

假设试验考察的变量为x1和x2,响应为y1、y2和y3,其均为望大质量特性的响应。如果在实际研究过程中,存在望小或者望目质量特性的响应,可对数据做简单的处理(比如加负号),将其转化为望大质量特性的响应。根据式(7)获得响应的贝叶斯后验样本抽样值后,第k(k=1,2,…,n)个试验点x(k)能够达到帕累托最优的概率可以通过式(9)和式(10)近似地求得。

∈PF(i))

(9)

(10)

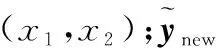
2 灰色关联分析

我国学者邓聚龙在1982年创建了灰色系统理论[37]。灰色关联分析是灰色系统理论的重要组成部分,现在已经被广泛应用于工程实践中。在灰色关联分析理论中,判断序列之间联系是否紧密的依据为序列曲线几何形状的相似程度。如果曲线几何形状的相似程度高,那么序列之间的联系就大,反之就小。早期主要以邓聚龙教授提出的灰色关联分析模型为代表,之后许多学者在其基础上提出多种灰色关联分析模型。

2010年,文献[37]在广义灰色关联模型的基础上提出灰色接近关联度模型,灰色接近关联度用于测量序列Xi和Xj在空间中的接近关联程度。Xi和Xj之间越接近,那么其之间的接近关联度ρij就越大,反之就越小。以灰色接近关联度理论为基础,将多响应优化得到的m组帕累托解{Yi}作为比较序列{yi(1),yi(2),…,yi(n)},i=1,2,…,m,将由n个单目标各自的最优解组成的{Y0}作为参考序列{y0(1),y0(2),…,y0(n)}。令

(11)

根据式(11)可计算序列Yi和Y0的灰色接近关联度为

(12)

式中,如果Yi和Y0长度相同,那么有式(13)成立。

(13)

在多响应优化设计中,灰色关联分析法能够将多响应优化问题转化为以灰色关联度为目标的单响应优化问题,并通过计算m组比较序列与参考序列之间的关联度来获得最佳因子组合和最佳响应目标值。

3 结合帕累托最优原则与灰色关联分析的多响应优化设计

在多响应优化设计的过程中,难点之一是如何解决多个响应之间可能存在的冲突问题。目前解决这类问题的方法主要有两种[38]:一种方法是选取其中一个响应作为目标函数,然后将剩余的响应作为约束条件,以此将多响应优化问题转化为求解有约束的目标函数的最优解问题;另一种方法是选择一个综合的目标函数,然后求解该函数的最优解,由此多响应优化问题被转化为单响应优化问题。然而,上述两种方法各自都存在一定的缺陷。选取其中一个响应作为目标函数或者选择一个综合的目标函数,这两种方法在很大程度上都受到主观因素的影响,而且不同的目标函数往往会得到不同的优化结果。因此,利用上述两种方法进行多响应优化设计,得到的优化结果通常是不完整的。利用帕累托最优原则的优势,构建多响应优化算法可以弥补上述方法的不足,从而能够客观地得出所有符合优化目标的参数值。故本文在贝叶斯多元回归模型统一框架下,针对在多响应优化设计中,模型参数的不确定性以及生产过程的噪声因子导致的预测响应值波动问题,首先采用帕累托最优原则获取一系列优化的参数设计组合,然后利用灰色关联分析方法,进一步确定最佳的参数组合。所提方法的基本流程如图1所示,具体步骤如下。

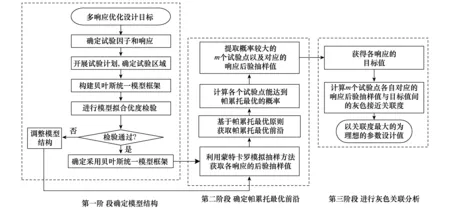
图1 所提方法的多响应优化设计流程图Fig.1 Flow chart of the proposed method for multi-response optimization design

步骤1采用中心复合设计的方法进行相关试验,根据试验条件,确定各个变量的试验区域。

步骤2构建贝叶斯回归模型统一框架,进行模型拟合优度检验。如果该模型通过拟合优度检验,则转入步骤3,反之,需调整模型结构,转入步骤3。

步骤4.1确定当前的抽样次数为m,如果m≤N,其中N为抽样总次数,则确定第m次模拟抽样后n个试验点的各个响应后验抽样值为

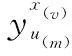
步骤4.2按照帕累托最优原则确定初始的帕累托最优前沿为

式中,1≤b≤i≤c≤j,此处令b=i=c=j=1。

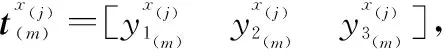
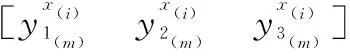
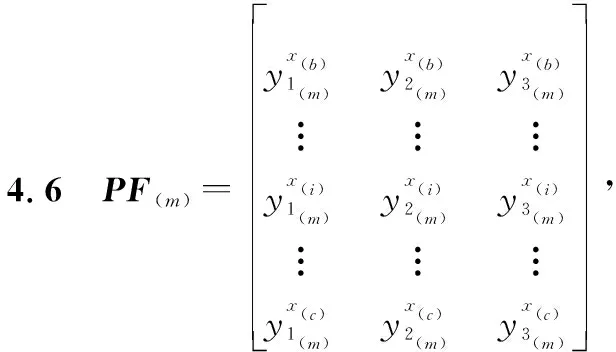
步骤4.7得到第m次抽样后的帕累托最优前沿PF(m)。令m=m+1,转入步骤4.1。

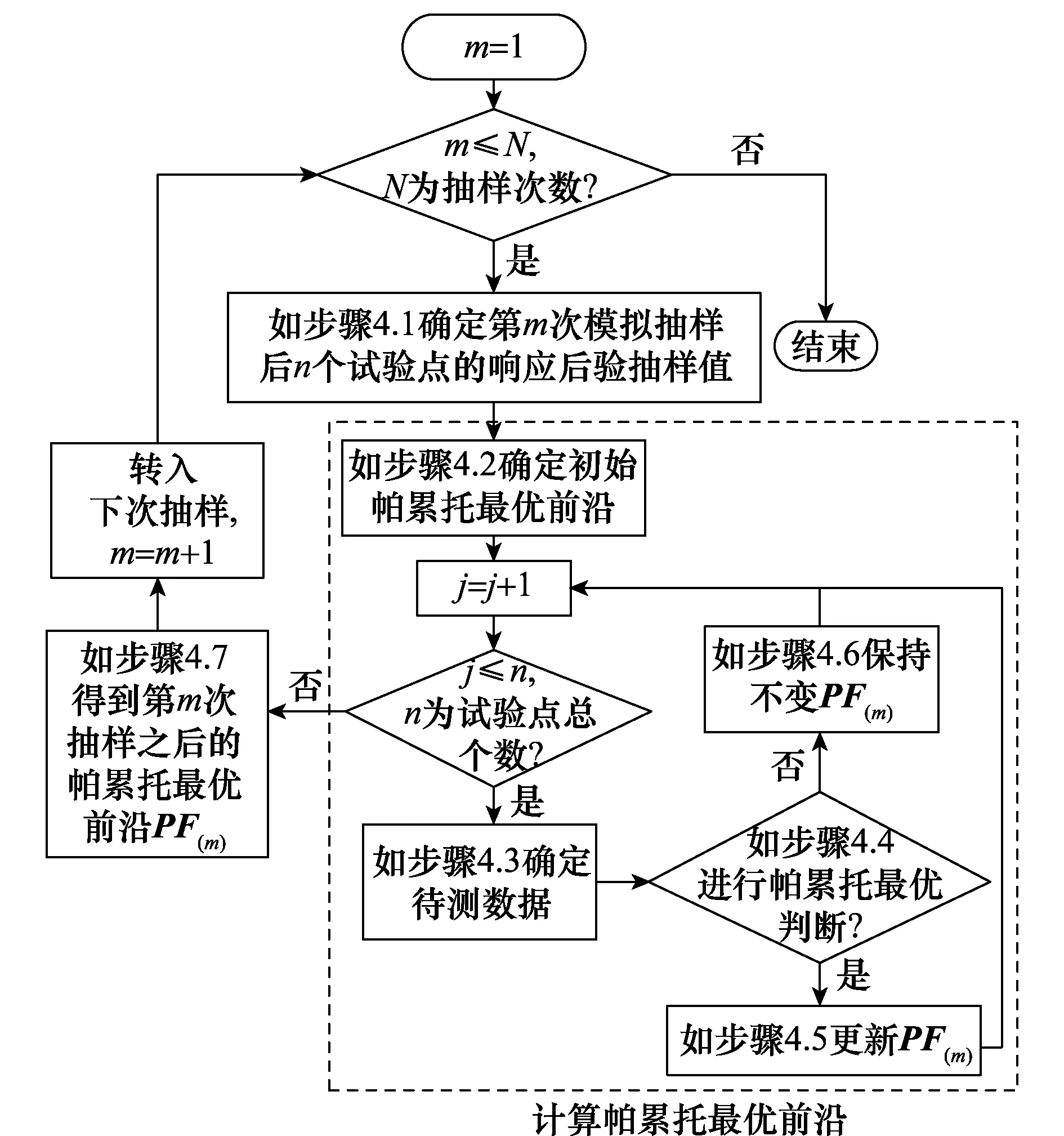
图2 计算帕累托最优前沿的算法流程图Fig.2 Flow chart of the algorithm for calculating the Pareto optimality frontier

步骤5利用步骤4的结果结合式(9)和式(10),计算每一组参数值在整个优化过程中能够达到帕累托最优的概率。

步骤6根据步骤5的结果,选择概率较大的m组参数值,利用其对应的响应后验抽样值进行灰色关联度分析,并按照灰色接近关联度进行排序,以关联度最大的为最优设计方案。在图2的基础上,结合前面5步的结果,灰色关联分析的算法流程如图3所示。

图3 灰色关联分析的算法流程图Fig.3 Flow chart of grey relational analysis

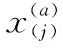
步骤6.6得到ρ(s),其中s=1,2,…,m。

步骤6.7选择ρ(s)最大的为最优设计方案,优化过程结束。

4 实例分析

4.1 实例背景

本试验旨在通过加拿大卡尔加里大学机械与制造工程系飞秒激光微纳加工中心实现某卫星芯片的微孔制造过程。该试验方案的设计以及数据收集工作系本文第一作者在加拿大卡尔加里大学从事博士后研究工作期间,与加拿大卡尔加里大学飞秒激光微纳加工中心的研究人员共同完成。该飞秒激光微纳加工中心主要由飞秒激光束发生器(femtosecond laser beam generator),微加工工作站(micro-machining workstation),工控制计算机(machining control computer)，测量仪器(measuring instrument)和花岗岩平台(granite platform)组成,具体实物如图4所示。在该试验中,选择直径y1和圆度y2作为关键的质量特性以反映某芯片微孔的几何特性和加工精度,其中直径为望目质量特性,而圆度为望大质量特性。此外,圆度与微孔的面积和主轴有关,其具体的公式定义为

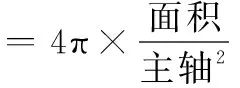
(14)

式中,通过图像软件Imagej分析微孔图片,可以获得式(14)中的微孔主轴和面积。影响上述两个响应的可控因素为平均功率x1(mw)、脉冲频率x2(Hz)和切削速度x3(mm/s),3个变量的水平和编码设置如表1所示。

图4 飞秒激光微纳加工中心Fig.4 Femtosecond laser micro/nano-machining center

参数水平-1.682-1011.682x115.9150100150184.09x2398500650800902x30.030.060.110.160.19

本次试验的目的是希望确定3个变量的最佳设置,从而使直径y1的目标值维持在21的水平上，并尽可能最大化圆度y2。本文采用中心复合设计开展相关试验，试验数据由实验人员通过实际的激光微钻实验收集，结果如表2所示。

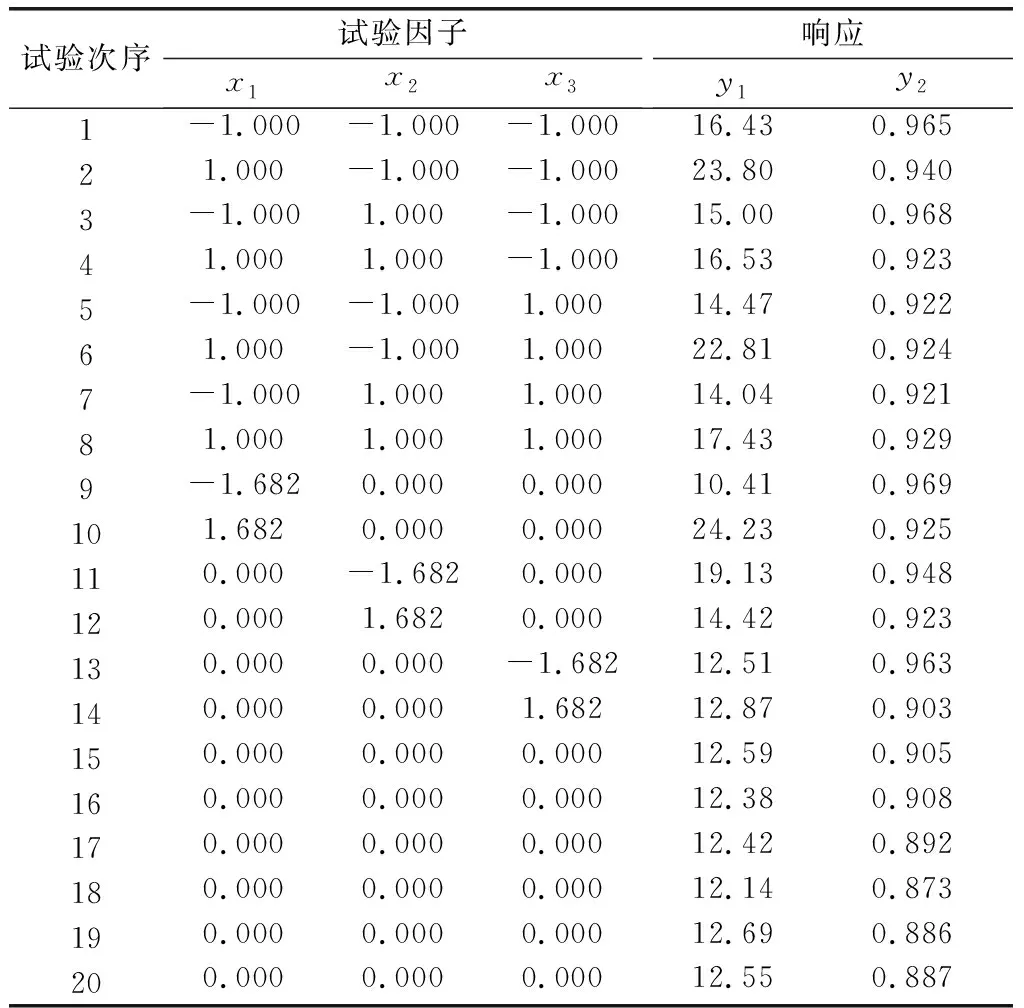
表2 中心复合设计试验结果

4.2 确定贝叶斯多元回归模型统一框架

在上述试验中,3个变量的可接受范围均为-1.68～1.68,取值间隔为0.38,整个试验区域包含729个试验点。在整个优化过程中,假设回归模型式(1)中的因子效应向量为

利用最小二乘法进行模型参数估计,计算结果如表3所示。

表3 模型拟合优度检验

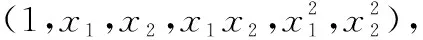
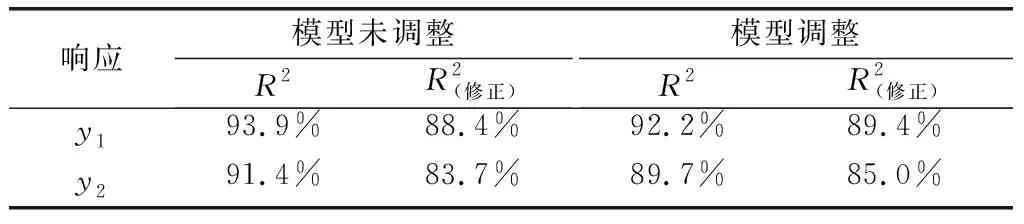
表4 模型y1和y2两次拟合优度对比

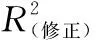
4.3 根据帕累托最优原则确定帕累托最优前沿

假设两个响应的目标值分别为21和1,试验的模拟抽样次数N为2 000次,根据式(3)～式(7)在试验区域内的每个点进行蒙特卡罗随机抽样,得到各自响应的后验抽样值。由于在实际操作过程中,圆度y2不存在大于1的值。因此如果该响应存在大量超过1的后验抽样值,需要将对应的试验点删除,最终试验区域中的待测试验点为603个。然后利用剩余试验点的后验抽样结果在试验区域内根据图2进行多响应优化。在R优化代码中,以矩阵的形式呈现随机变量W和U的模拟抽样结果。最后根据每次优化得到的帕累托最优前沿,根据式(9)和式(10)计算每个试验点能够达到帕累托最优的概率,其研究结果如图5所示。

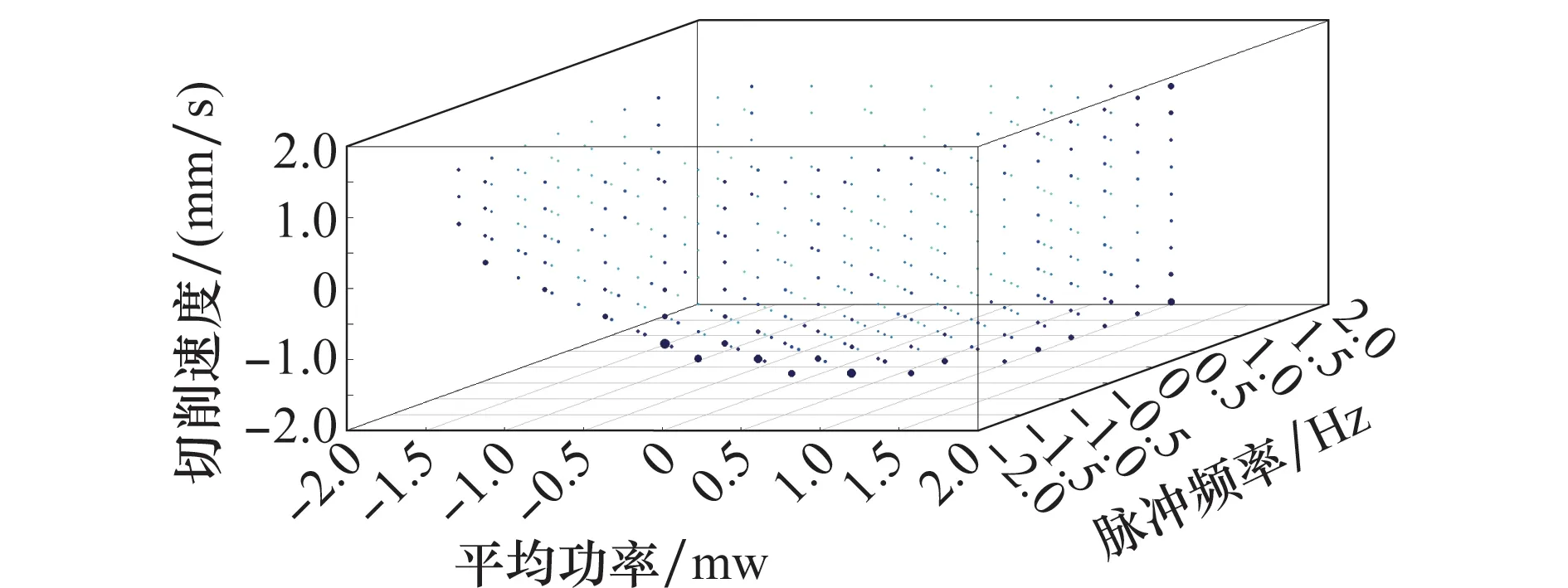
图5 按照帕累托最优原则确定帕累托最优前沿Fig.5 Determining the Pareto optimal front based on the Pareto optimal principle

图5中的圆点为整个试验过程中所有分布在帕累托前沿上的试验点，即这些点在整个优化过程中至少有一次出现在帕累托前沿上。每个圆点的大小和颜色与该点在整个优化过程中能达到帕累托最优的概率有关，点越大，颜色越深，在该点处能达到帕累托最优的可能性越大。另外，图中的圆点大小不同，颜色深浅不一，这表明预测响应值的波动问题对优化结果产生了较大影响，这种波动问题主要来源于模型参数的不确定性以及生产过程的噪声因子。由图中点的分布位置可知，最有可能达到帕累托最优的试验点主要分布在图形的下方区域。

本例提取了整个试验过程中前8个最有可能达到帕累托最优的试验点，这8个试验点对应的响应后验抽样值变化见图6。

图6 8个试验点关于两个响应的箱形图Fig.6 Boxplots of two responses on the eight test points

比较分析图6中各个试验点针对不同响应的优化效果可知,在上述多响应优化设计的实例中,如果仅考虑响应y1上的优化效果,则第294号、329号、372号和603号试验点给出的结果明显优于其他试验点。如果仅考虑响应y2上的优化效果,则以上8个点与目标值都存在一定的差距,第293号、327号、328号和372号试验点的优化效果略高于其他试验点。因此,根据图6可知,除了第373号试验点,这些可重复性较高的试验点至少在一个响应上能够得到较好的优化效果,这与帕累托最优的定义一致。此外,表5给出了8个试验点各自能达到帕累托最优的概率。

分析表5的优化结果可知,在本文的多响应优化设计实例中,第372号试验点能达到帕累托最优的可能性相对较高,而第373号试验点的可重复性概率最低。图6中第372号试验点在两个响应上都能得到较好的优化效果,而第373号试验点关于两个响应的优化效果相对较差,可见表5和图6给出的结果一致,进一步说明了该优化结果是可靠的。

表5 图6中的试验点能够达到帕累托最优的概率

4.4 基于灰色关联分析的多响应优化

在上述试验的优化过程中,运用本文所提方法获得了8组优化结果。此处运用灰色关联分析方法,对表5中的8组结果进行排序。为此,将本例中各个响应的目标值{21.000,1.000}作为参考序列,根据图3计算每组解对应的响应后验抽样值与参考序列之间的灰色接近关联度,计算其平均值作为该组解与参考序列的灰色接近关联度,按照此关联度对8组解进行排序,以关联度最大的作为最优设计方案。灰色关联分析法的研究结果如表6所示。

表6 灰色关联分析结果

结合表6的分析结果可知,第372号、329号和第294号试验点的灰色关联度非常接近,这3个也是可重复性概率相对较高的试验点。其中,第372号试验点的关联度略大于其余两个试验点,应为本次试验的最优结果,其对应的两个响应值分别为20.886 9和0.968 1。此外第603号和第373号试验点的关联度较接近,而第327号、第328号和第293号试验点的关联度差距不大。虽然前者在响应y2上的优化效果略低于后者,但是在响应y1上的优化效果明显优于后者。所以在表5中排名靠后的第603号和第373号试验点的关联度略大于第327号、第328号和第293号试验点。可见,针对预测响应值存在波动的多响应优化问题,运用本文所提的方法,能够从可重复性和关联度两个方面获得较为满意的结果。

5 结 论

在多响应优化设计中,往往需要考虑预测响应值波动对优化结果的影响。本文在贝叶斯回归模型的统一框架下,结合帕累托最优策略和灰色关联分析方法,提出了一种多响应优化设计的新方法。该方法在多响应优化设计过程中同时考虑了模型参数不确定性和生产过程中噪声因子的影响,并结合贝叶斯后验概率方法计算试验点能够达到帕累托最优的概率,然后利用灰色关联分析方法进一步确定理想的参数值。另外,通过实例证明该方法对解决预测响应值存在波动的多响应优化问题是有效的。

需要特别指出的是,本文中试验区域的选择具有主观性,该案例仅有3个变量,2个响应,试验区域较小,利用蒙特卡罗模拟抽样方法和帕累托最优策略能够快速地得到帕累托最优前沿。如何在变量和响应个数增加时选择合适的试验区域,有待进一步地深入研究。此外,本文的研究基于贝叶斯多元回归模型的统一框架,在模拟优化过程中,假设各个响应的模型结构完全一致,如何利用SUR模型进行多响应优化设计,以考虑各个响应模型的结构对多响应优化结果的影响,这是今后需要研究的课题之一。另外,尽管SUR模型能够更精确地拟合响应模型,但是在SUR模型的贝叶斯建模过程中其模拟响应的抽样速度非常缓慢,这也是未来研究过程中有待解决的关键科学问题之一。