吉林省蒙古栎树高级材积表编制初探

兰 莹

(长春市净月潭实验林场，吉林 长春 130117)

材积表是量测森林资源数量和质量的度量衡。使用精确的度量衡对森林资源调查、森林采伐限额管理、森林资源档案管理、控制森林资源消耗、提高森林资源利用率等都具有重大意义。以往我省编制的一元立木材积表只考虑胸径一个因子，未考虑树高差异对立木材积的影响，造成适用精度不高，而二元材积表需要观测每株树木的胸径和树高，在实际工作中非常繁琐，加大调查人员的工作强度，本文以全省蒙古栎测定数据探索编制树高级材积表，旨在低强度工作量基础上，提高测算精度。

1 数据的收集与整理

1.1 数据收集要求

编表样木和检验样木应根据现实林分分布、资源数量等状况，相对均匀分布于编表区域和不同的立地条件、经营措施、林龄、树高级、郁闭度等级内。

每个径阶的树高分布要近似呈正态分布，所选的样木好、中、差都要有样木分布。

收集各径阶应保证25株，15株用于编表，10株用于验表。

样木树高≤10 m的采用1 m区分，树高>10 m的采用2 m区分。

1.2 数据整理

本项研究数据取自全省各县市区，经3倍标准差法对原始样木数据进行筛选后，最终选取编表样木1 903株，验表样木1 254株，具体见表1。

表1 编验数据

2 基准树高导向曲线导算

2.1 基准树高导向曲线的选择

树高曲线方程的种类很多，有的采用抛物线方程，有的采用幂函数曲线式等。本次编表为了既保证精度又便于计算，选用下式作为模拟胸径与树高方程。

H=a+b/(D+k)

式中：D——胸径；

H——树高；

A、B、K——求算的参数。

2.2 基准树高方程参数

采用H=a+b/(D+k) 进行模拟，回归模拟参数见表2。

2.3 基准树高方程精度检验

用实际值与估测值，通过绝对误差、回归标准差、回归标准误的计算，对树高方程的精度进行检验，检验结果见表3。

2.4 适用性检验

为了检验树高方程的适用性，利用收集的检验样本进行F检验和系统误差计算。F检验结果、系统误差见表4。

表2 树高方程参数

表3 树高方程精度检验

表4 树高方程F适应性检验

从表4可以看出，计算出来的F值均小于F0.05的值，计算的系统误差均在±3 %以内，符合编表要求。

3 编制方法

就树高的分级而言，可以做出多种分法，树高级的划分与立地指数的划分都是以树高为依据，二者类似，利用立地指数表划分树高级的方法用于编制树高级材积表是科学合理的，也是最有效的，本办法已被实践多次证明，在国内也多次被使用。编制材积表采用二元材积式导算一元材积表方法编制。

3.1 标准径阶的确定

根据树高与胸径的分布特点，通过多方面分析，选取接近中间值的26 cm径阶做为标准径阶。

3.2 树高级距的确定

由原始材料分析得知，26 cm径阶树高最小、最大值分别为13.4 m到21.8 m,变动幅度8.4 m。按级距2 m划分，共划分5级。胸径为26 cm时，各树高级的分布值依次为13 m、15 m、17 m、19 m、21 m。

3.3 各等级树高曲线的推导

推导各等级树高曲线，是以基准导向曲线为基轴，采用标准差调整法导算各树高级曲线。

His=Hki+[Hs0-Hk0]×Sai/Sa0

His:欲求算的S树高级于i胸径时的树高值；

Hki:基准树高曲线上胸径值为i时的树高值；

Hs0:S树高级标准径阶的树高值；

Hk0:基准树高曲线上标准径阶时的树高值；

Sai: 胸径为i时的回归剩余标准差；

Sa0:标准径阶时的回归剩余标准差。

3.3.1 计算各径阶树高标准差

各测高木按径阶归并后，计算平均树高，然后计算各径阶树高标准差。

SYh=SQR[∑(Hi-H0)2/(N-1)]

SYh:树高标准差；

Hi:i径阶树高；

H0：i径阶平均树高；

N：i径阶株数。

3.3.2计算各径阶标准差与标准径阶标准差的比值

P=Sai/Sa0

Sai: 胸径为i时的回归剩余标准差；

Sa0: 标准径阶时的回归剩余标准差。

3.3.3整列标准差比值

将计算的各径阶标准差与标准径阶标准差的比值(Sai/Sa0)按P=D/(a+bD+cD2)公式进行整列。

P=D/(2.8459+2.3872D-0.016D2) 相关系数0.9738。

4 树高级材积表编制

利用各等级树高曲线的推导公式计算求出5个树高级在各种不同胸径状态下的树高值。将树高值带入蒙古栎二元材积式(V=0.000 048 27D1.704 675 91H1.225 218 57)，计算树高级材积表，具体见表5。

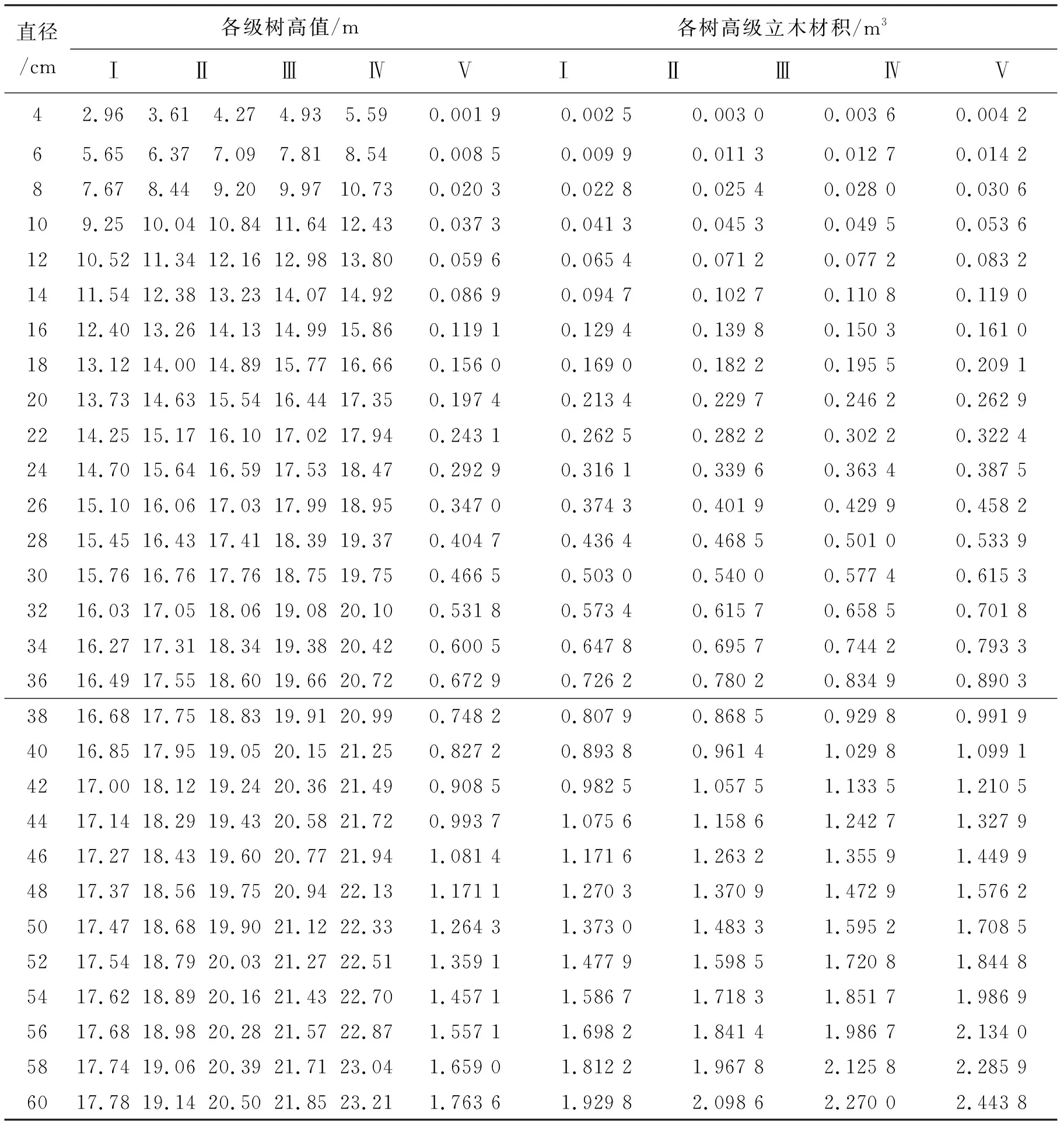
表5 蒙古栎树高级材积

5 结论

根据各树高级的不同树高值编制材积表，能明显看出树高分级后，等于将其全部范围划分为多个层次，将树高值本身大幅度变动范围分割开来，将各类型树木分别划归不同的树高级，从而提高了立木材积的计算精度。

树高级的确定方法是将林分平均直径树高整列公式和各等级树高曲线计算公式，求出此胸径值在5个树高级状态下的不同树高值，然后再将林分平均高与5个树高级树高值进行对比，最接近数值所代表的树高级便是此林分的树高级。

编制的树高级材积表是在广泛收集样木的基础上进行的，从而使编制出材积表有较充分的基础与根据。不但解决了一元立木材积表精度不高、适用性不强，二元材积表工作任务繁琐，调查强度大等难题，还为在低强度工作量基础上，提高测算精度提供新思路。