基于高光谱的复垦农田土壤有机质含量估测①

石朴杰，王世东，张合兵，王新闯



基于高光谱的复垦农田土壤有机质含量估测①

石朴杰，王世东*，张合兵，王新闯

(河南理工大学测绘与国土信息工程学院，河南焦作 454000)

为了快速准确估算矿区复垦土地土壤有机质含量，以永城矿区复垦农田为例，在土样机质含量测定和高光谱数据测量的基础上，对土壤高光谱数据进行多种预处理并与有机质实测含量进行相关性分析，利用相关系数进行=0.01水平显著检验，确定敏感波段，建立一元线性回归、多元逐步回归和偏最小二乘回归等多种有机质含量与高光谱估测模型。结果表明：经过数学变换的土壤光谱反射率与土壤有机质含量相关性显著提高，复垦区土壤光谱经过多元散射校正和一元微分处理并利用偏最小二乘回归模型建模预测效果最好。当前较少有研究对矿区复垦农田土壤有机质进行高光谱估测，本研究成果可为有效利用高光谱遥感技术，快速、有效地测定复垦农田土壤有机质含量提供技术支撑。

高光谱；复垦农田；土壤有机质；估测模型

土壤有机质(soil organic matter，SOM)是决定土壤肥力的重要指标之一，为植物提供需要的营养元素，素有植物的“养分银行”之称[1-3]，因此，土壤有机质含量的快速、准确监测对农业可持续发展具有重要的意义。而传统的土壤有机质测试方法具有耗时、费力、成本高等缺点，并且结果滞后难以满足当前生产管理的需要[4]。而高光谱分析技术因其波段多、分辨率高、数据量丰富等特点，可以快速、高效、低成本对土壤有机质进行实时监测[5-8]。对煤矿区复垦农田土壤有机质进行高光谱遥感分析，进而对煤矿治理区土壤质量进行动态监测与评估，可为区域土地复垦质量评价提供一定的理论依据。

自20世纪60年代，国内外许多专家学者已经开始对土壤有机质与土壤光谱关系进行了研究。Bowers和Hanks[9]研究发现，对土壤有机质进行氧化处理，能使土壤的反射系数提高8.2%。Baumgardner等[10]在测定室内土壤光谱时发现可见光比近红外区域更适合预测有机质含量。Karnieli和Verchovsky [11]发现土壤有机质吸收特征主要出现在1 720、2 180和2 309 nm处。Barthès等[12]测定了非洲不同粒径砂质土的有机质含量和近红外光谱，分析了其相关关系。从1980年以来，国内逐步开始了对土壤有机质含量与其光谱的研究。卢艳丽等[13]利用570 ~ 590 nm波段的一阶导数光谱和1 280 nm处反射峰高度较好地预测了东北主要土壤类型的有机质含量。于雷等[14]通过对比高光谱4种预处理变换形式，得出土壤光谱反射率经过连续统去除变换，并建立偏最小二乘回归模型效果最佳。沈润平等[15]在对原始高光谱数据进行预处理的基础上，分别建立了多元线性逐步回归模型和人工神经网络模型，并对模型进行分析比较，得出人工神经网络法优于多元线性逐步回归法的结论。

综上所述，国内外针对土壤高光谱估测已经有了大量的研究，肯定了土壤中的有机质含量等在可见光-近红外光谱预测上的能力。国内利用可见光-近红外光谱反演滩涂地区、麦田耕作层、水稻土、荒漠土、干旱区绿洲[16-20]土壤等较多，较少有对矿区复垦农田土壤有机质高光谱估测进行研究。南锋等[21]对黄土高原煤矿区复垦农田土壤进行高光谱波段的全波段、一阶微分和倒数的对数处理3种变换形式与土壤有机质含量的相关性分析，并且通过建立偏最小二乘回归预测模型，对复垦区土壤有机质含量进行了估测。而本研究则是以河南省永城矿区复垦农田土壤为研究对象，通过采集土样，化验分析，光谱测定，对测得的光谱数据进行多种变换，分析土壤光谱与有机质含量的相关性，确定敏感光谱波段，通过对比分析一元线性回归、多元逐步回归和偏最小二乘回归法，建立矿区农田土壤有机质含量高光谱估算模型，确定适合矿区复垦农田土壤有机质含量估测的最佳组合，为矿区复垦农田土壤有机质估测提供一定的参考。

1 材料与方法

1.1 研究区概况

河南省永城市位于豫、皖交界地带，东部和北部与安徽省接壤，复垦区位于淮河冲积平原北部，地势平坦，地形西北高，东南低，微向东南倾斜，地理位置116°39′ E，33°91′ N。复垦区表土层由黏土、亚黏土、中细粉砂土组成。农田土壤适宜小麦、玉米、棉花等多种农作物生长，耕作制度为一年两熟或两年三熟。研究区原为河南神火集团新庄煤矿的塌陷地，地面最高点与最低点相差5 m，形成大面积积水。土地复垦后，坡度为3‰，达到了土地耕种的要求。

1.2 土样采集与有机质测定

土样采集利用“S”形布点法，使用螺旋取土钻取5个点的0 ~ 20 cm表土层，充分混合作为一个样品。共采集33个样品，土壤样品经自然风干，去除植物残体和杂物后混合均匀，将每个样本分为2份，将充分研磨过20目筛样本用于高光谱数据测定。采用重铬酸钾容量法-外加热法[22]测定土壤有机质含量。将33个样本随机分为2组，选用23个样品用于建模(占总样本的70%)，10个样品用于验证(占总样本的30%)，样品的有机质含量见表1。

表1 土壤样本集有机质含量统计

1.3 土壤光谱测定

复垦区土壤高光谱数据的测定采用美国ASD (Analytical Spectral Device)生产的FieldSpec 3型光谱仪，光谱范围350 ~ 2 500 nm。波段为350 ~ 1 000 nm的光谱分辨率为3 nm，其采样间隔为1.4 nm；波段为1 000 ~ 3 500 nm的光谱分辨率为10 nm，采样间隔为2 nm。重采样间隔为1 nm。土壤光谱测量时，在四周漆黑的实验室里，将土壤样品放置于直径为10 cm，厚度为2 cm，并用直尺将样品表面刮平。将视场角为25°探头垂直置于距土壤样本表面15 cm上方，光谱仪自带的50 W卤素灯为样本提供光源，光源距土壤样本50 cm，照射角度45°。考虑到土样表面的平整度和土壤颗粒有可能会对测量结果产生影响，每个土样测4个方向的光谱(转3次，每次90°，每个方向5条光谱曲线)，共20条曲线，取其平均值作为该土样的光谱曲线。

1.4 光谱数据预处理

由于光谱曲线的350 ~ 400 nm和2 400 ~ 2500 nm受外界噪声影响较大，所以考虑将其去除，以减少干扰。为比较光谱不同的预处理方法对建模产生的影响，本文采用了标准正态变换(standard normal variate transfor­mation，SNV)、多元散射校正(multiple scatter correction，MSC)、Savitzky-Golay 9点平滑(Savitzky- Golay smoothing with 9 points，SG)、微分处理(一阶微分，first derivative，1D；二阶微分，second derivative，2D)、倒数的对数(inverse-log reflectance，IR)、倒数(inverse，IN)、连续统去除(continuum removal，CR)对原波段光谱反射率(reflectance，R)进行预处理。SG平滑变换可以减少杂点，降低曲线对比度；MSC变换可以消除土壤颗粒的不均匀；经过SNV处理可以消除表面散射；光谱微分处理可以降低噪声影响的敏感性，分辨重叠光谱，提高分析精度；倒数的对数变换可以减少因光照变化而造成的影响[14, 23-24]；连续统去除处理有利于压抑背景光谱，突出光谱曲线的吸收和反射特征[25]。并且，不同的预处理方法的组合，可以提高所建模型的精度。

1.5 敏感波段的选择

在复垦区土壤有机质高光谱预测建模的敏感波段的选择上，通常选用土壤有机质与光谱反射率的各种变换形式进行相关性分析，相关系数范围1.0 ~ –1.0，相关系数的绝对值越大，表示其相关性越高，波段越敏感。本文通过对光谱反射率进行的各种数学变换与土壤有机质含量进行相关性分析，得到的相关系数进行=0.01水平上的显著性检验，通过显著性检验的波段用于土壤有机质含量高光谱模型的估算。

1.6 估测模型建立

本文分别采用一元线性回归、多元逐步回归和偏最小二乘回归建立土壤有机质高光谱模型。

一元线性回归是统计学最常见的分析方法，是一对一的关系。其数学表达式：

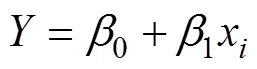
多元线性逐步回归法是常用统计建模方法，该方法常被用来确定所研究目标物中某种化学成分的敏感性，以此来确定敏感波段，用得到的敏感波段值来估计这种化学成分的浓度值，其模型表达式为：

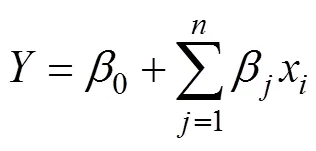
偏最小二乘回归(partial least squares regression，PLSR)可以同时实现两组之间的相关性、数据结构化以及回归建模，在处理因变量较多或者具有较强自相关性，而样本量较少的数据时具有一定的优势，并且有对数据降维，简化数据结构，去除噪声干扰，综合筛选特征的特点，被认为是具有较大建模潜力的方法[26-27]。

1.7 模型检验

模型的检验选用决定系数(determination coeffi­cients，2)、均方根误差(root mean squared error，RMSE)和统计量值3个参数进行评定。

2是相关系数的平方值，用来衡量模型的稳定性，2越大，模型越稳定，其计算公式为：

RMSE用来判定模型的预测能力，是预测值与实测值的符合度。RMSE越小，模型精度越高，预测能力越好，其计算公式如下：

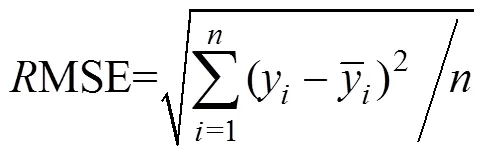
统计量反映的是回归方程所能解释的变差与不能解释的变差的比例。其数学定义为：

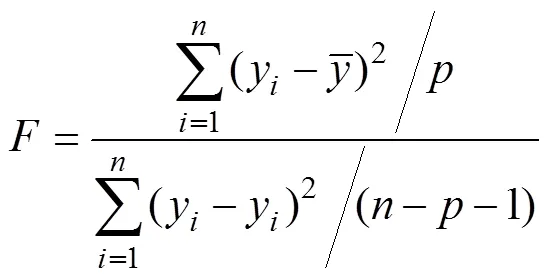
当统计量值大于理论临界值a并且值越大，2越高，RMSE越小时，说明模型的估算准确性越高，反之则模型估算的准确性越差。

2 结果与分析

2.1 土壤有机质与光谱的相关性分析

分别对土壤有机质含量与R、SNV、SNV与1D组合、SG、SG与1D、SG与2D组合、MSC、CR、IN和IR进行相关性分析，并通过=0.01水平的显著性检验，结果如图1所示。从图1可知，土壤有机质含量与光谱R、IN、IR相关性较小，没有波段通过=0.01显著水平，故不宜用作提取敏感波段进行高光谱模型的估算。而光谱经过SNV和MSC变换后，相关性均有所提高，并且显著波段相同，说明SNV与MSC效果相同。本文采用MSC数据进行下一步分析。而光谱经过1D、2D、CR和MSC+1D变换均有部分波段通过了=0.01显著性水平检验，因此用其进行高光谱模型的建立。

与原始波段R相比，经过数学变换土壤光谱反射率与土壤有机质含量的相关性显著提高。与原始波段相比，光谱反射率经MSC变换通过=0.01显著性检验的敏感波段为可见光谱波段的508 ~ 562 nm；光谱反射率SG+1D变换的敏感波段主要集中在475 ~ 534、1 392 ~ 1 461、2 168 ~ 2 215 nm；光谱反射率SG+2D变换的敏感波段主要集中在426 ~ 557、1 410 ~ 1 413、1 642、2 249 nm等；光谱反射率MSC+1D变换的敏感波段主要为422 ~ 445、611 ~ 691、1 423、1 477、1 684 nm等，光谱反射率CR变换的敏感波段以可见光波段549 ~ 585 nm为主，剩下的主要为短波红外，而近红外波段则无敏感波段。经过SG+2D变换的光谱波段与土壤有机质含量在457 nm处出现最大正相关，相关系数为0.66；经过SG+1D变换的光谱波段与土壤有机质含量在1 422 nm处出现最大负相关，相关系数为–0.68；经过SG+1D预处理并通过=0.01显著性水平检验挑选出来的敏感波段分布全面，对光谱的充分表达充有一定的积极作用。

2.2 模型的对比分析

2.2.1 一元线性回归模型 选取有机质含量与经过数学变换的波段相关系数绝对值的最大值为自变量，样品的有机质含量的实测值为因变量，建立一元线性回归模型(表2)。

从表2建立的4个有机质含量一元线性回归模型来看，模型的决定系数2和统计量最高的是SG+2D，分别为0.53和23.94，说明在一元线性回归模型中经SG平滑和2D变换是最优选择，但是其RMSE是5个模型中最高的，又2虽然是4种变换中最高的，但是数值为0.53，调整后的2为0.51，拟合度较低，因此一元线性回归分析模型效果较差。

图1 土壤有机质含量与光谱反射率及变换形式的相关系数

表2 有机质含量一元线性回归模型

2.2.2 多元逐步回归模型 选取经过数学变换的敏感波段为自变量，样品的有机质含量的实测值为因变量，建立多元逐步回归模型。从表3中多元逐步回归模型的检验结果来看，与一元线性回归模型相比，总体多元逐步回归所建模型决定系数2均有所提高，其中SG+2D的决定系数2提高了0.31，而MSC+1D的决定系数2则从0.34提高到了0.84，其他变换模型的决定系数2也均有不同程度的提升，说明多元逐步回归模型要优于一元逐步回归。其中的原因是单个波段不能很好地表达光谱特征，而多个波段相互组合能更好地表达光谱信息。从绘制的土壤有机质实测值与预测值的散点图(图2)可见，经CR和MSC模型验证样本偏离1︰1线比较严重，而SG+1D、SG+2D、MSC+1D验证样品则相对更靠近1︰1线，SG+2D验证模型决定系数2达到了0.82，是3个验证模型决定系数中最高的，而RMSE为0.88，同时也是3个模型中最低值，验证一个模型的好坏2越高，RMSE越低，模型的精度越高，总体来说，对波段经SG平滑的2D变换挑选的敏感波段进行多元逐步回归建模更能体现模型的精度。

表3 有机质含量多元逐步回归模型

图2 有机质含量多元逐步回归模型估算值与实测值的比较

2.2.3 偏最小二乘回归模型 将样本有机质含量的实测值作为因变量，选取经过数学变换的敏感波段为自变量，建立偏最小二乘法逐步回归模型。结合有机质含量多元逐步回归模型，5种变换分别建模的决定系数2和统计量均有所提高，均方根误差RMSE有所降低。虽然SG+2D的决定系数2仅提高了0.01，但其均方根误差RMSE则从2.52降到了0.99，统计量从28.4升到178.97，提高了150.57，偏最小二乘法回归模型相比多元逐步回归模型总体来说精度有所提高。

图3为有机质含量偏最小二乘回归模型估算值与实测值的比较，SG+1D、CR和MSC模型验证样品偏离1︰1线较严重，SG+2D、MSC+1D验证样品基本在1︰1线附近，而MSC+1D的验证决定系数2达到了0.91，RMSE为0.72，与SG+2G相比具有明显的优势。因此，MSC+1D在偏最小二乘法回归模型中表现最优，估算精度最高。

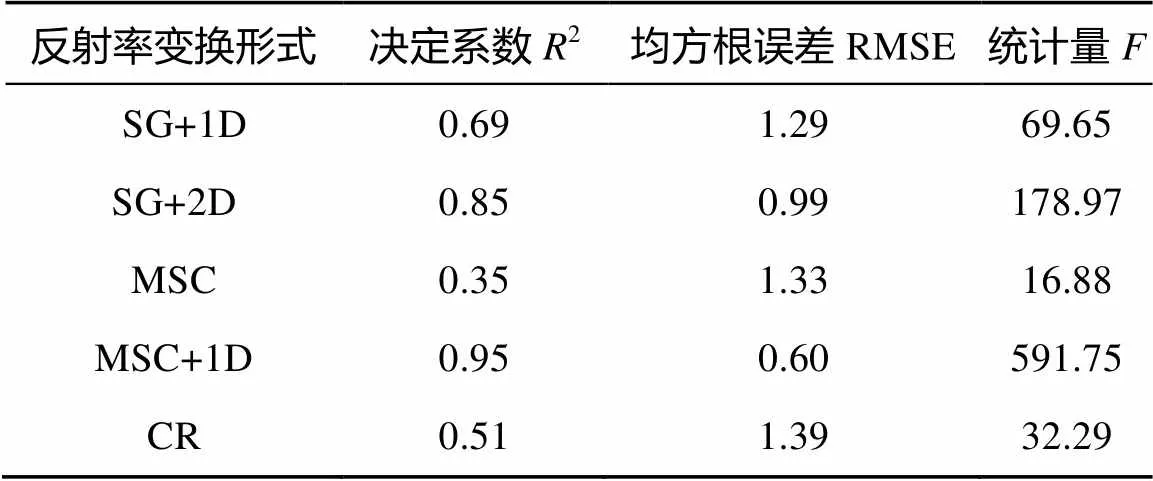
表4 有机质含量偏最小二乘回归模型精度

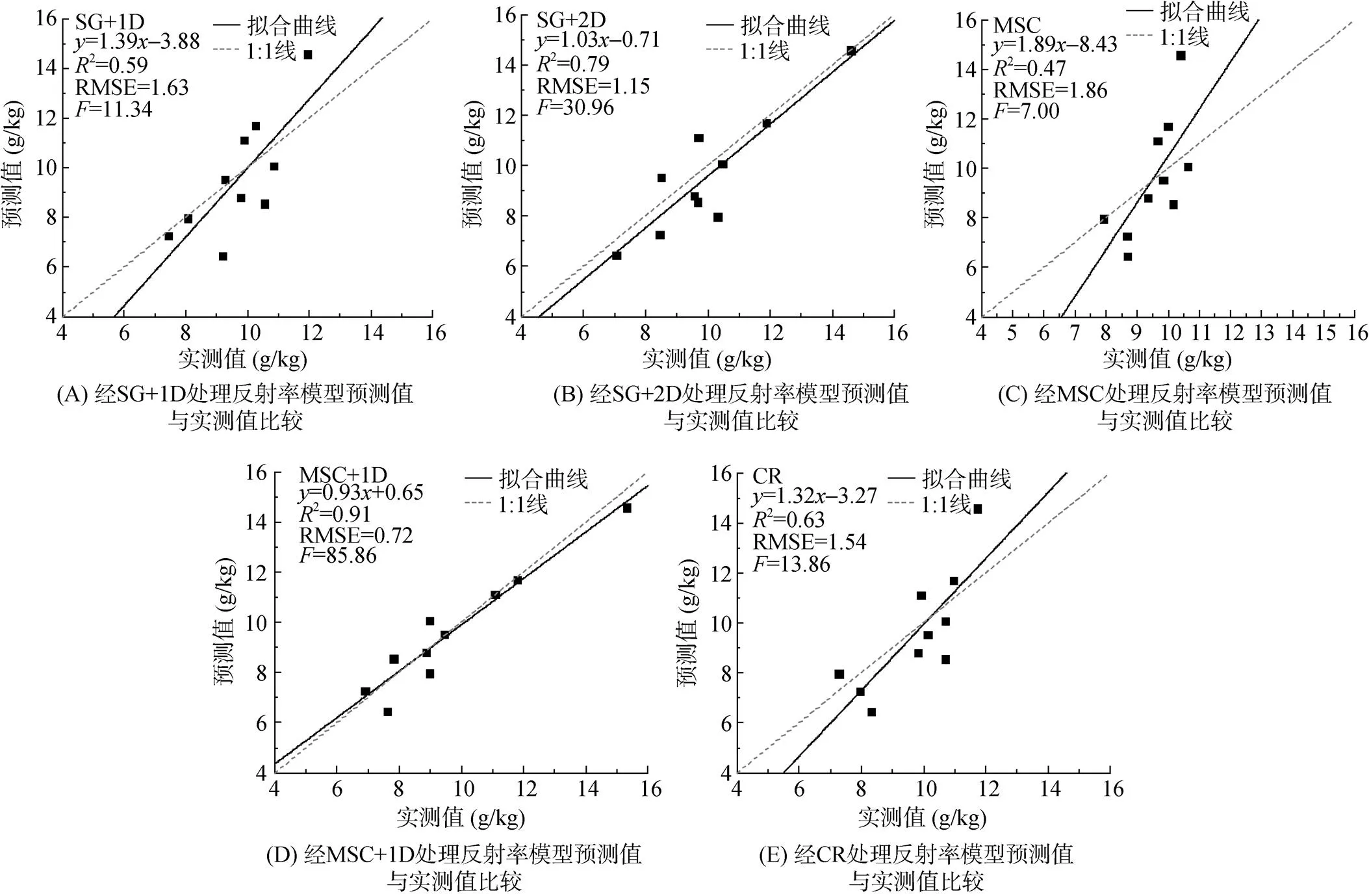
图3 有机质含量偏最小二乘回归模型估算值与实测值的比较

从研究结果来看，偏最小二乘回归模型中，光谱反射率经MSC+1D变换与有机质含量的决定系数2和统计量是所有光谱数据波段变换中最高的，分别达到了0.95和591.75，均方根误差RMSE达到最低，为0.60，并且验证模型决定系数2为0.91，曲线拟合度最高，这与郭斗斗等[28]得出MSC与一阶微分相结合在光谱模型中表现最优相符合，土壤高光谱数据经过MSC+1D与MSC处理对比分析可知，使用两种预处理算法，其与有机质含量相关性更高，同时对建模精度也有很好的提升，一种预处理不能更全面地消除其他因素的干扰，两种预处理方法的结合，能提高显著波段相关性，进一步使模型精度提高。

通过对建立的复垦区有机质含量一元线性回归模型、多元线性回归模型和偏最小二乘法回归模型3个模型的比较分析，一元线性回归模型的决定系数均小于0.6，精度偏低，效果较差，不适合作复垦区有机质高光谱遥感估测。相比较一元线性回归模型，多元线性回归模型的精度有显著的提高，其中高光谱波段经过SG平滑的2D变换的多元线性回归模型的决定系数2达到了0.84，并且验证模型决定系数2为0.82，在多元线性回归模型所有的数学变换中是最优的。相较多元逐步回归模型，无论使用哪种预处理的方法，偏最小二乘回归模型的精度均有所提高，这与郭斗斗等[28]、候艳军等[18]、李媛媛等[29]通过多种模型对比分析得出的结论基本一致。

3 结论

本研究结果表明，煤矿复垦区土壤高光谱反射率经过数学变换，与土壤有机质含量相关性显著提高，并且经过MSC与1D相结合的数学变换，并建立偏最小二乘回归模型的预测精度最高，模型稳定性最好，其验证模型决定系数达到0.91，统计量为85.86，RMSE达到0.72。本文以永城市煤矿塌陷复垦区土壤有机质为研究对象建立的预测模型，可为其他煤矿复垦区土壤有机质预测提供参考，对进行矿区土地复垦监测提供技术支撑，为大面积土地复垦指标体系的快速建立提供依据。

[1] 中国土壤学会. 土壤农业化学分析方法[M]. 北京: 中国农业科技出版社, 2000

[2] 吕贻忠, 李保国. 土壤学[M]. 北京: 中国农业出版社, 2006: 317–318

[3] 张枝枝, 张福平, 燕玉超, 等. 渭河两岸缓冲带的土壤有机质含量分布特征及其影响因子[J]. 土壤, 2017, 49(2): 393–399

[4] 贺军亮, 蒋建军, 周生路,等.土壤有机质含量的高光谱特性及其反演[J]. 中国农业科学, 2007, 40(3): 638–643

[5] Yang H, Kuang B, Mouazen A M. Quantitative analysis of soil nitrogen and carbon at a farm scale using visible and near infrared spectroscopy coupled with wavelength reduction[J]. European Journal of Soil Science, 2011, 63(3): 410–420

[6] 洪永胜, 于雷, 朱亚星, 等. 基于EPO算法去除水分影响的土壤有机质高光谱估算[J]. 土壤学报, 2017, 54(5): 1068–1078

[7] 张瑶, 李民赞, 郑立华, 等. 基于近红外光谱分析的土壤分层氮素含量预测[J]. 农业工程学报, 2015, 31(9): 121–126

[8] 吴才武, 夏建新, 段峥嵘. 土壤有机质测定方法述评与展望[J]. 土壤, 2015, 47(3): 453–460

[9] Bowers S, Hanks R. Reflection of radiant energy from soil[J]. Soil Science, 1965, 100(2): 130–138

[10] Baumgardner M F, Stoner E R, Silva L F, et al. Reflective properties of soils//Brady N. Advances in agronomy, 38. New York: Academic Press, 1985: 1–44

[11] Karnieli A, Verchovsky I. Geographic information system for semi-detailed mapping of soils in a semi-arid region[J]. Geocarto International, 1998, 13(3): 29–42

[12] Barthès B G, Brunet D, Hien E, et al. Determining the distributions of soil carbon and nitrogen in particle size fractions using near-infrared reflectance spectrum of bulk soil samples[J]. Soil Biology & Biochemistry, 2008, 40: 1533–1537

[13] 卢艳丽, 白由路, 杨俐苹, 等. 基于高光谱的土壤有机质含量预测模型的建立与评价[J]. 中国农业科学, 2007, 40(9): 1989–1995

[14] 于雷, 洪永胜, 耿雷, 等. 基于偏最小二乘回归的土壤有机质含量高光谱估算[J]. 农业工程学报, 2015, 31(14): 103–109

[15] 沈润平, 丁国香, 魏国栓, 等. 基于人工神经网络的土壤有机质含量高光谱反演[J]. 土壤学报, 2009, 46(3): 391–397

[16] 徐明星, 周生路,丁卫, 等. 苏北沿海滩涂地区土壤有机质含量的高光谱预测[J]. 农业工程学报, 2011, 27(2): 219–223

[17] 王超, 冯美臣, 杨武德, 等. 麦田耕作层土壤有机质的高光谱监测[J]. 山西农业科学, 2014, 42(8): 869–873

[18] 侯艳军, 塔西甫拉提·特依拜, 买买提·沙吾提, 等. 荒漠土壤有机质含量高光谱估算模型[J]. 农业工程学报, 2014, 30(16): 113–120

[19] 向红英, 柳维扬, 彭杰, 等. 基于连续统去除法的南疆水稻土有机质含量预测[J]. 土壤, 2016, 48(2): 389–394

[20] 周倩倩, 丁建丽, 唐梦迎, 等. 干旱区典型绿洲土壤有机质的反演及影响因素研究[J]. 土壤学报, 2018, 55(2): 313–324

[21] 南锋, 朱洪芬, 毕如田. 黄土高原煤矿区复垦农田土壤有机质含量的高光谱预测[J]. 中国农业科学, 2016, 49(11): 2126–2135

[22] 鲍士旦. 土壤农化分析[M]. 北京: 中国农业出版社, 1999: 30–34

[23] 褚小立, 袁洪福, 陆婉珍. 近红外分析中光谱预处理及波长选择方法进展与应用[J]. 化学进展, 2004, 16(4): 528–542

[24] 梁卓娅. 土壤有机质的近红外光谱信息提取及定量分析[D]. 山西太谷: 山西农业大学, 2016

[25] Clark R N, Roush T L. Reflectance spectroscopy: Quantitative analysis techniques for remote sensing applications[J]. Journal of Geophysical Research Solid Earth, 1984, 89(B7): 6329–6340

[26] 史舟, 王乾龙, 彭杰, 等. 中国主要土壤高光谱反射特性分类与有机质光谱预测模型[J]. 中国科学: 地球科学, 2014, 44(5): 978–988

[27] 方少文, 杨梅花, 赵小敏, 等. 红壤区土壤有机质光谱特征与定量估算——以江西省吉安县为例[J]. 土壤学报, 2014, 51(5): 1003–1010

[28] 郭斗斗, 黄绍敏, 张水清, 等. 多种潮土有机质高光谱预测模型的对比分析[J]. 农业工程学报, 2014, 30(21): 192–200

[29] 李媛媛, 李微, 刘远, 等. 基于高光谱遥感土壤有机质含量预测研究[J]. 土壤通报, 2014, 45(6): 1313–1318

Estimation of SOM Content in Reclaimed Cropland Based on Hyperspectra

SHI Pujie, WANG Shidong*, ZHANG Hebing, WANG Xinchuang

(School of Surveying and Land Information Engineering, Henan Polytechnic University, Jiaozuo, Henan 454000, China)

Thirty-three soil samples were collected from the reclaimed farmland in the coal mining areas in Yongcheng in order to estimate quickly and accurately SOM content by hyperspectra, in which 23 samples and 10 samples were used to establish and verify the hyperspectral models respectively. SOM contents and hyperspectra of the soil samples were measured, the correlations were analyzed between SOM content and the multi-pretreated hyperspectral data, correlation coefficients at= 0.01 level were used to test to determine the sensitive bands, and models of simple linear regression, multiple stepwise regression (MSR) and partial least squares regression (PLSR) were established. The results showed that transformed soil spectral reflectance promoted the correlation coefficients, and PLSR models of the differential spectra were optimal after the spectral noise were reduced by multiple scattering correction. Due to little information is available now on hyperspectral inversion of SOM content in reclaimed farmland, the above results provide technical support for the efficient and rapid determination of SOM content in reclaimed farmland by using hyperspectral remote sensing.

Hyperspectra; Reclaimed land; SOM, Estimation model

国家自然科学基金项目(41301617)、中国煤炭工业协会指导性计划项目(MTKJ-2015-284)、中国博士后科学基金项目(2016M590679，2015M580629)、河南省高等学校重点科研项目(17A420001，16A420003)、河南省高校基本科研业务费专项资金项目(NSFRF1630)、河南理工大学创新性科研团队项目(B2017-16)、河南省高校科技创新团队支持计划项目(18IRTSTHN008)和河南理工大学青年骨干教师资助计划项目资助。

(wsd0908@163.com)

石朴杰(1989—)，男，河南周口人，硕士研究生，主要研究方向为矿区开采沉陷与土地复垦。E-mail：dssomx@163.com

10.13758/j.cnki.tr.2018.03.017

S151.9

A