变形协调条件下非线性破坏准则的加筋土坡临界高度上限解

胡卫东，谭建辉，曾律弦，张泰来(.湖南理工学院土木建筑工程学院，湖南 岳阳 44006；. 湖南大学岩土工程研究所，湖南 长沙 4008；.香港大学土木工程系，香港 999077)

土工合成加筋材料已广泛应用于边坡、路堤和挡土墙等工程结构中，其稳定性分析理论与方法的研究一直受到人们关注，极限分析上限法无需准确确定破坏机构内部的应力分布，而且能满足材料本构关系、位移和边界条件，因此成为分析加筋边坡稳定性的一种有效方法。

在已有加筋边坡稳定性理论研究中，多数都局限于线性Mohr-Coulomb破坏准则，然而，岩土介质服从非线性破坏准则，线性破坏准则只是其中一个特例[1～4]，非线性强度是岩土体非常重要的材料强度特性，对岩土工程力学行为有重要影响，因此，在极限分析方法中引入非线性破坏准则进行加筋边坡稳定性研究更符合实际工程需要。

国内外学者利用极限分析上限理论研究加筋土边坡稳定性已取得很多重要成果，Porbaha等[5～6]基于上限理论采用对数螺旋面破坏机构研究了加筋土坡的临界高度，并利用离心模型试验进行验证研究；Jewell等[7]利用极限分析理论给出了加筋陡坡的设计图表；Michalowski等[8～9]、Radoslaw等[10～11]假设筋材的破坏形式为拉伸破坏，通过计算滑动层内筋材拉力所做的功对加筋土进行了研究；崔新壮等[12]研究了3种不同布筋模式对土坡临界高度及滑裂面形状与位置的影响；吴雄志等[13]假设筋材为拔出破坏，建立了通过坡角滑动破裂面的土工织物加筋土坡稳定性的上限解；阙云等[14]结合竖直条分平移破坏机构建立加筋路堤稳定性计算公式，探讨了多种因素对稳定性的影响；邓国瑞等[15]在非关联流动法则下研究了加筋土边坡的稳定性问题；李秀娟等[16]基于广义塑性理论的上限法研究了筋材能量耗散的计算。加筋边坡内土工筋材的能量耗散计算是应用极限分析上限方法确定其临界高度的关键，上述研究成果在一定程度上反映了水平分布筋材的力学变形机理，但并没有充分考虑到极限状态下滑动破坏面上筋材与土体会产生协调变形，致使加筋边坡相应协调变形下的许可速度场发生改变，筋材能量耗散计算公式也产生相应变化，其临界高度确定方法必然存在较大差别。因此，针对滑动破坏面上筋材与土体协调变形的特点展开深入研究，正是本文研究的核心内容。

为此，本文将结合加筋土坡的工程性质和力学变形机理，考虑破坏间断面滑动层上筋材与土体变形协调特点及速度变化的连续性，分开计算素土内力功和间断面上筋材能量耗散功率，基于非线性破坏准则和外切线法，利用上限分析理论建立直线破裂面和对数螺线破裂面的加筋土坡临界高度计算模型，以期完善加筋土坡稳定性分析理论与方法。

1 非线性破坏准则

Zhang等[17]建立了Power-law非线性破坏准则来描述岩土材料的非线性强度关系，其表达式如下：

(1)

式中：c0，σt，m——岩土材料参数；

c0——曲线与纵轴的截距；

-σt——曲线与横轴的截距。

曲线恒定通过(0，c0)和(-σt，0)两点，m决定了曲线的弯曲程度，如图1所示。m=1时，式(1)则转变为线性破坏准则。

图1 非线性破坏准则曲线及切线Fig.1 Curve of a nonlinear failure criterion and its tangential line

对式(1)求导可得σn-τ曲线的切线斜率，切线完全位于破坏曲线外侧，切线斜率(曲线的曲率)随着σn的增加而逐步减小：

(2)

在上限分析中，经常有学者采用“在结构的任何部分提高材料的屈服极限，不会降低结构的极限荷载”这一思想，由真实屈服面的外接屈服面计算得到的极限荷载，也将是真实极限荷载的上限解[18～19]。因此，在按实际屈服条件求解问题有困难的情况下，基于非线性破坏准则的上限分析可采用外切直线法，相应提高岩土材料的屈服强度来获得上限解，这种外切直线破坏准则下的上限解一定为真实的非线性破坏准则极限荷载的上限。

外切直线L的方程式为：

τ=ct+tanφtσn

(3)

式中：ct，tanφt——切线的截距和斜率。

如图1所示，ct，tanφt的表达式为：

(4)

(5)

2 筋材的能量耗散分析方法

加筋土坡内筋材的能量耗散分析方法是应用极限上限分析理论确定其临界高度的关键，为了建立合理的筋材能量耗散分析方法，首先作如下基本假定：

(1)n层筋材均匀水平布置在土坡内，土体内摩擦角为φ，基于小变形条件下，加筋土坡问题可视为平面问题；

(2)假定破坏间断面上筋材与土体变形协调，边坡土体达到极限状态破坏时，筋材产生拉伸断裂破坏，且筋材有足够的锚固长度而不被拔出；

(3)土体服从相关联流动法则，且本文的水平加筋材料为土工格栅、土工织物等柔性筋材，即不考虑其抗弯刚度的影响。

基于以上假定对筋材的能量耗散进行分析，取破坏间断面上的Δl微段作为研究对象，由于不考虑筋材的抗弯刚度,筋材只能承担拉力，随着荷载的增加,滑动层内的筋材会随土体的滑动变形而逐渐改变其受拉方向。加筋土体达到极限状态时沿着某一速度间断面破坏，筋材与土体在间断面薄滑动层上将会产生协调变形，为了最大程度地阻止土体发生滑动，变位后薄滑动层内筋材的方向应被动调整为与滑块间断速度[V]相反的方向[20～21]，如图2所示。设薄滑动层厚度为t，破坏间断面与水平方向的夹角为ξ，本文假定土体服从相关联流动法则，则间断速度[V]与间断面成φ夹角。同理，当破坏间断面为对数螺线面时,滑动层内变位后的筋材方向与该处的曲率半径相垂直。

图2 微段Δl内筋材的能量耗散Fig.2 Energy dissipation of reinforcement in segment Δl

设筋材变位前采用均匀布筋模式，竖向等距离布置水平筋材，如图3所示，加筋层单位宽度极限抗拉强度为Tt，则加筋土坡内筋材的平均抗拉强度kt可以表示为：

图3 布筋模式Fig.3 Reinforcement distribution modes

(6)

(7)

式中：d——筋材竖向间距；

H——加筋土坡高度。

筋材与土体产生协调变形后，滑动破坏层内筋材的间距d′可由图2中的几何关系求得，即：

(8)

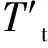
(9)

当运动滑块相对于静止滑块运动时，在速度间断面这一薄滑动层内，从相对静止部分过渡到相对运动部分，筋材上任意连续点的速度方向与间断面成φ角，其大小满足变化的连续性，这里假设其为简单的线性变化，表达式为：

(10)

式中：s——筋材上任意点变位后在滑动层内的长度；

V——滑动层内筋材任意点的速度矢量；

[V]——间断速度矢量。

(11)

于是，可求得土坡内单层筋材每单位宽度的能量耗散率为：

(12)

综合上述，联立式(9)与(12)则可求出间断面上单位面积的筋材能量耗散率dr′：

(13)

3 直线破裂面加筋土坡

对于加筋土坡，假定土坡的破裂面为直线破裂面，如图4所示的屈服机构，刚性滑块ABC沿AB面下滑，间断速度为[V]，其方向与破裂面成φ角。ABC刚性滑块在自重作用下的外力功率为：

图4 直线破裂面屈服机构-速度场Fig.4 Failure mechanism for a linear crack surface

(14)

式中：β——边坡坡角；

γ——土体重度；

θ——直线滑裂面与水平面的夹角。

加筋土坡内能耗散率包括两部分，一部分为AB速度间断面上能量耗散率，其表达式为：

(15)

式中：c——岩土体黏聚力。

另外一部分为筋材的能量耗散，因直线破裂面机构中ξ夹角与θ夹角相等，于是可得筋材的能量耗散率为：

(16)

(17)

(18)

(19)

基于非线性破坏准则，采用其破坏曲线的强度参数ct和φt，代入式(19)则可得非线性破坏准则下加筋土坡临界高度表达式为：

(20)

非线性破坏强度准则中，ct和φt参数随应力状态σn大小而变化，将式(4)和式(5)代入式(20)，临界高度H可表示为以θ及φt为变量的函数式，即：

H=H(θ，φt)

(21)

(22)

将求解获得的θ及φt代入式(21)，即得土坡临界高度上限解：

Hc=H(θ，φt)min

(23)

4 对数螺线破裂面加筋土坡

加筋土坡稳定性分析经常按对数螺线曲面或圆弧滑动面进行研究。这里假定滑动破裂面为通过坡脚A的对数螺线面AB，如图5所示的屈服破坏机构，破裂面的曲线方程可表示为式(24)，机动许可速度场为刚性滑块ABC绕极点O转动的运动模式，速度间断面上任意点的间断速度由式(25)表示。

图5 对数螺线破裂面屈服机构Fig.5 Failure mechanism for the logarithmic spiral crack surface

由对数螺线方程式：

R=R0e(θ-θ0)tanφt

(24)

V=V0e(θ-θ0)tanφt

(25)

V0=ωR0

(26)

式中：R0——极径OB的长度；

θ0——极径OB与水平面夹角；

V0——B点间断速度;

ω——刚性滑块的转动角速度。

由几何关系可得：

(27)

(28)

式中：Ls——BC之间的距离；

θh——极径OA与水平面夹角。其他符号见图5所示，图中3个参数θ0，θh及H即可完全确定土坡滑动面所在位置。

土体重力在ABC区域做功功率可以先分别求出OAB区域、OCB区域及OCA区域土重所做功率，然后再求三者代数和即可得到[22]，其表达式为：

(29)

(30)

(31)

(32)

速度间断面上素土的内能耗散率为：

(33)

(34)

f4=[e2(θh-θ0)tanφt-1]

(35)

由前面式(13)给出的速度间断面单位面积上筋材能量耗散率可以计算出整个对数螺线速度间断面上筋材的能量耗散率为：

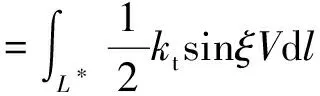
(36)

(37)

(38)

将式(24)、(25)、(27)及(28)代入式(36)可得：

(39)

求解可得:

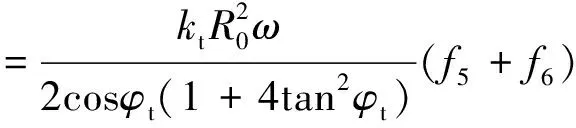
(40)

f5=e2(θh-θ0)tanφtsin(θh-φt)-sin(θ0-φt)

(41)

f6=2tanφt[e2(θh-θ0)tanφtcos(θh-φt)-cos(θ0-φt)]

(42)

在极限状态下任何机动容许的速度场，加筋土体重力所做功率等于速度间断面上素土内能耗散功率和筋材能量耗散功率之和，加筋土坡对应高度为临界高度。

(43)

于是，可得到：

(44)

非线性破坏准则下，θ0参数与应力状态σn紧密相关，将式(4)和式(5)代入式(44)，H函数式则为θ0，θh及φt为变量的函数，即：

H=H(θh，θ0，φt)

(45)

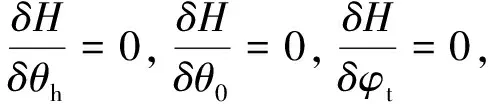
(46)

将求解获得的θh、θ0及φt代入式(45)，即得土坡临界高度上限解：

Hc=H(θh，θ0，φt)min

(47)

5 算例分析

5.1 分析模型与优化算法的验证

为了验证本文加筋土坡临界高度分析模型和优化算法的正确性，本文采用对数螺线滑裂面破坏机构计算结果与采用加筋土离心模型试验的文献[6]、[23]和[24]结果，及同样引入上限极限理论计算加筋土坡临界高度的文献[25]计算结果进行对比分析与讨论，如表1所示。为了更好地进行对比分析，取m=1，将问题简化为线性破坏准则下的临界高度上限求解。

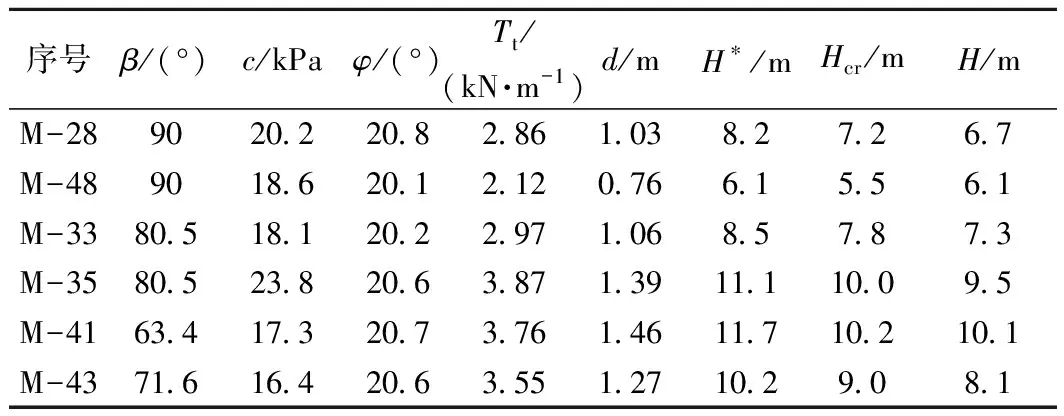
表1 离心模型试验及理论分析的临界高度Table 1 The critical height of centrifugal model test and theoretical analysis

注：试验数据为文献[6]、[23]和[24]的模型离心试验结果；地基土重度γ=17.8 kN/m3，其他参数见表1；H*、Hcr和H分别为模型离心试验、文献[25]理论计算及本文理论计算的临界高度值。

通过对比计算结果可以看出，本文方法计算结果与文献[25]计算结果较接近，且本文计算临界高度值略小，是较优的上限解，主要是考虑了间断面薄滑动层上变形的协调性及速度变化的连续性，这在一定程度上说明了本文分析模型和优化算法的正确性和合理性；本文及文献[25]计算得到的临界高度值均比试验实测值小，在10%～20%之间，主要是理论计算方法考虑的是破坏面上筋材能量耗散，而忽略了内部土层筋材与土的摩擦能耗，另外，离心模型试验箱壁与模型间的摩擦力也会产生一定误差。

将本文方法计算结果与A.Porbaha加筋土离心试验结果、文献[26]和[27]的理论计算结果进行对比分析，如表2所示。表中Hc为加筋土坡裂缝开始出现时的高度，Hf为加筋土坡倒塌破坏时的高度。通过比较可以看出，本文与文献[26]和[27]同样都是采用上限极限分析方法进行研究，三种理论方法计算结果非常接近，且本文所得上限解更优。

表2 临界高度理论计算结果对比Table 2 Comparison of critical height

5.2 非线性破坏准则对临界高度的影响

为了研究非线性破坏准则对加筋土坡临界高度的影响，结合以上表1中M-48工程算例，m=1时土重度γ=17.8 kN/m3，c=18.6 kPa，φ=20.1°，即可得到相应非线性强度参数下的破坏公式τ=18.6(1+σn/50.8)1/m，然后分别计算m=1.2～3.0，加筋土坡临界高度值，计算结果如表3所示。

表3 计算结果比较Table 3 Comparison of computation results

从表3中可以看出，建立考虑变形协调条件下加筋土坡临界高度分析模型，采用非线性破坏准则求解，随着m的增大，临界高度值逐步减小。

6 结论

(1)本文从加筋土坡的工程特性和变形机理出发，考虑破坏间断面滑动层上筋材与土体的变形协调特点及速度变化的连续性，研究得到破坏间断面上筋材能量耗散功率计算公式。

(2)引入上限分析方法，建立直线破裂面和对数螺线破裂面机构的加筋土坡临界高度确定方法，并利用序列二次规划优化算法得到上限解。

(3)对于岩土材料，非线性破坏准则更符合工程实际情况，引入非线性强度假设很有必要。非线性参数m对加筋土坡临界高度有着重要影响，随着m的增大临界高度值减小。