穿透曲线随流量升高的变化特征及预测
赵小二,常 勇,吴吉春,彭 伏(南京大学地球科学与工程学院,江苏,南京 210023)
岩溶含水层是全球范围内一种重要的供给水源,为世界上25%以上的人口提供了水资源。岩溶管道发育促进物质的循环和运移,因此,岩溶含水层特别容易遭受污染。岩溶含水层介质呈高度非均质和各向异性,高度脆弱,这种情况下达西定律几乎不适用[1],多孔介质特有的参数没有明确的物理意义。因此,岩溶含水层水流和运移特性高度复杂。这种背景下,定量示踪试验是一种有力工具,不仅能确定两点之间的水力联系,提供有关地下水运动轨迹的直接信息,还能给出穿透曲线(BTC),从中可以获得岩溶含水层中的溶质运移情况。可以通过BTC特征参数(峰值浓度、峰值时间等)直观了解溶质运移情况,也可以通过数学模型拟合BTC得到溶质运移参数,因此穿透曲线十分重要。水动力条件对穿透曲线的作用明显,因此不同流量条件下需要针对性进行示踪实验。可以通过足够多示踪实验来包含可能出现的水流条件,但野外条件下由于财力和时间限制,这种方案很难实现[2]。因此,研究穿透曲线随流量的变化规律,并根据流量预测得到BTC特征参数,可以对上述问题有个初步的解决。
许多学者研究了岩溶管道溶质运移同流量的关系。Morales等[3]对不同流量条件下多个岩溶管道的示踪试验数据进行分析,建立了穿透曲线特征参数之间以及与流量的关系式;Massei等[4]和Morales等[5]采用两种不同的溶质运移模型拟合不同流量条件下的岩溶管道示踪试验结果,分析了溶质运移参数随流量的变化趋势,并推断出穿透曲线拖尾很大程度上受水动力条件的控制;Göppert等[6]通过示踪实验调查研究了两种流量条件下溶质和胶体在岩溶管道中的运移特性,观测到高流量条件下穿透曲线的峰值浓度较大;Dewaide等[7]给出不同流量条件下洞穴系统示踪试验曲线的模拟结果和溶质运移参数,并讨论了溶质运移参数随流量的变化规律;赵小二等[8~9]把岩溶管道概化为水箱-管道系统,通过室内实验研究了溶潭结构和流量条件对穿透曲线的影响。虽然前人讨论了穿透曲线形状和溶质运移参数随流量条件的变化,但示踪实验只在少数几种流量条件下开展,关于流量条件变化对溶质运移的影响研究不够系统。因此,本文在赵小二等[9]研究的基础上,设计9种不同管道流量,在同一种管道结构条件下变化出口流量开展重复性实验,同时为了使研究结果更具有普遍性,设计三种管道结构,分别开展示踪实验。通过分析管道出口处的BTC,得到一系列参数,然后分析曲线形状和运移参数随着流量的变化规律,接着拟合BTC特征参数之间以及特征参数与流量间的特征关系式,预测最大和最小流量条件下的BTC特征参数,同时对比分析不同管道结构BTC的不同。
1 实验方法
为了研究岩溶管道中溶质运移随流量条件的变化规律,分别在同一种管道结构,9种不同的流量条件下进行示踪实验。实验装置主要由一个定水头供水水箱,1根圆管和两种不同形态的立方体水箱构成,对实验装置的描述请参见文[9]。
为了使研究结果更具有普遍性,分别在3种管道结构中开展一系列示踪实验:首先设计1个单管实验(图1a),然后在距离溶质注入点60 m的管道位置处分别添加对称水箱(图1b)和不对称水箱(图1c)。两种水箱的尺寸相同,边长都为10 cm,只是出入口位置不同,有关两种形态水箱的具体描述请参见文[9]。管道由内径为19 mm的透明软管构成,示踪剂注入点到管道出口的长度为101.1 m,在实验过程中,由于实验室空间有限(大小为15 m×10 m),管道在地面的摆放方式近似于矩形形状(图2)。相比较赵小二等[9]的研究,本文中的最大流量明显较大,为了确保最大流速水流条件下能获得足够多的浓度数据点,设计更长的管道。
选取质量浓度为100 g/L的NaCl溶液作为示踪剂,通过注射器瞬时注入2.5 mL体积的示踪剂溶液到管道中,注入质量为0.25g。NaCl溶液被用作保守型示踪剂,管道出口示踪浓度通过电导率测量值来确定。通过LWGY系列涡轮流量计测量管道流量,仪表精度为±1.0%。为了确保流量数据的稳定性,设计从供水水箱出口到涡轮流量计的管道长度为6 m,为了确保示踪剂注入点之后管道流场的稳定性,设计电磁流量计出口到示踪剂注入点的管道长度为2 m。每次实验在流量稳定几分钟后再开始注入示踪剂。每组实验重复3次,确保重复曲线的结果无明显差异。岩溶管道中地下水流常呈紊流状态,流速通常大于裂隙和孔隙介质[10]。因此,计算的雷诺数通常需要大于4 000[11],确保实验在紊流条件下开展。

图1 不同管道结构的示意图(俯视图)Fig.1 Schematic diagram showing different pipe structures (top view)
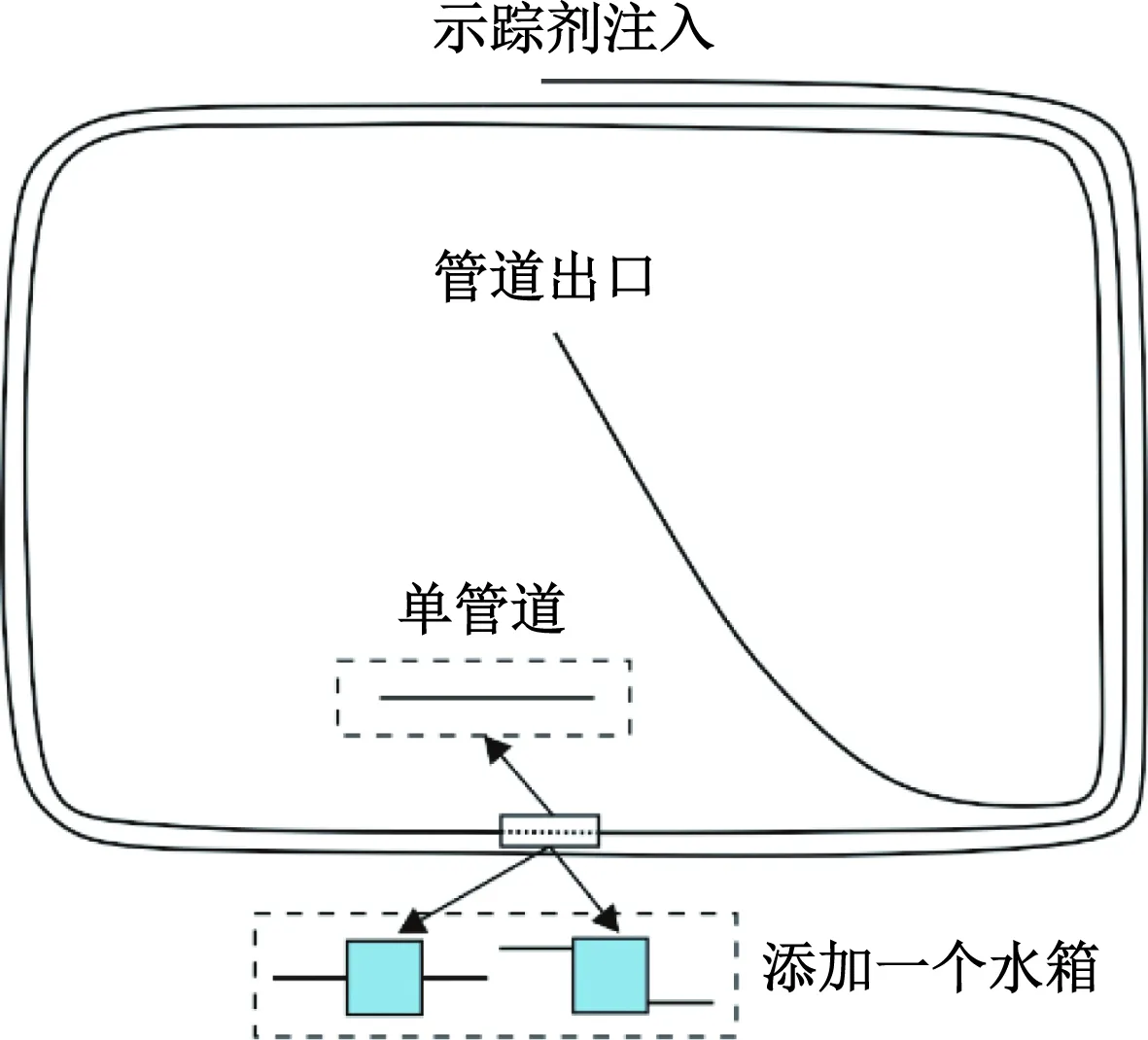
图2 管道摆放位置示意图(俯视图)Fig.2 Schematic diagram of the pipe placement (top view)
2 参数计算方法
按照实验步骤,每组实验可得到3种特征曲线:示踪剂穿透曲线(tracer BTCs)、示踪剂质量流量曲线、停留时间分布(RTD)曲线,通过3种曲线获得一系列参数(表1)。根据Field等[12~13]研究结果可知,Qtracer2软件[14]可对岩溶水文系统的水动力学特性和运移特性进行合理评价,广泛应用于野外示踪实验BTC的分析[4, 15~16]。表1中的部分参数可以通过Qtracer2软件获得,其他参数可通过经验公式或统计方法求解得到,求得的参数值见表2。其中弥散系数(Dchat)通过Qtracer2软件中内置的Chatwin方法[17]进行求解。将可描述湍流圆管中溶质运移的一维对流弥散方程[18]在瞬时注入条件下的浓度解析解公式变形得到:
(1)
以式(1)的左侧为纵坐标、时间为横坐标,把示踪浓度曲线数据点绘制在图中,其中Ap=Cptp1/2。通过直线的纵坐标截距求得弥散系数(Dchat),通过斜率求解平均流速(v)。发现浓度分布的前缘数据点在图中呈线性下降,后缘拖尾数据点偏离直线,因此穿透曲线拖尾段不能通过Taylor方程[18]进行描述。
如果示踪浓度在空间上的分布对称,则C=Cp=Aptp-1/2,Ap=Cptp1/2。Davis[19]和Day[20]等指出对于不对称的浓度分布,通过该式计算Ap带来的误差非常小,另外Chatwin[17]指出式(1)的左侧项关于t的曲线形状对Ap的值不敏感,只有t=x/v附近的数据点对所采用的Ap值比较敏感,因此本文采用Ap=Cptp1/2。

表1 根据示踪实验数据得到的主要参数Table 1 Main parameters obtained from the data of tracer experiments
通过示踪穿透曲线获得与运移时间、流速和示踪剂浓度相关的参数,如示踪剂首次检出时间(t1)、示踪剂最后检出时间(t2)、优势流速(vp)和峰值浓度(Cp)等。取示踪剂注入时间t=0作为参考,记录不同的时间t。管道长度101.1 m为注入点到取样点的径向距离x的值。
流量随着时间基本不变,通过每个时刻的浓度和流量相乘得到示踪剂质量流量曲线。对该曲线进行积分得到溶质回收质量,回收质量和注入溶质质量的比值为回收率。
将质量流量除以回收质量得到RTD,RTD曲线的积分面积为1。RTD表示瞬时注入的示踪剂在t和t+dt这个时间段停留在系统中的概率密度函数[21],即示踪剂从管道系统中流出的时间分布[22]。通过RTD定量化系统的基础混合响应,可与其他系统进行对比,或者可以预测研究系统在不同条件下的行为特征[23]。Jobson[24]采用单位-响应曲线去表征河流中的溶质运移,即为了使响应曲线的值接近于1,将RTD值乘以106。本文为了使曲线的值接近于1,将RTD曲线值乘以102作为单位-响应曲线。RTD可以计算平均运移时间、平均示踪速度、方差和单位峰值浓度的值,即单位-响应曲线的峰值。
3 示踪剂穿透曲线
每组实验重复3次得到的穿透曲线几乎相同,说明实验结果的稳定性。从表2中可以看出,所有示踪实验的雷诺数都大于5 000,说明管道内水流呈紊流状态,且回收率超过85%,表明比较满足质量守恒规律。回收率低于100%,一方面可能因为注入过程中示踪剂有泄露,另一方面可能由于电导率仪器的监测频率低导致少量数据点未被监测到。
实验得到的示踪剂穿透曲线见图3,所有曲线的特征是:明显呈单峰,且浓度以相对较快的速度增大至最大值,接着以较缓慢的速度逐渐下降,曲线有不同程度的拖尾。随着管道流量的升高,3种结构的峰值浓度均逐渐增大,曲线宽度逐渐缩小,曲线拖尾程度逐渐减弱(图3),示踪剂最先检出时间明显提前,溶质云持续时间逐渐缩短,运移时间方差逐渐降低(表2)。曲线拖尾逐渐减弱,直观表明了穿透曲线的拖尾受水动力条件的控制,与前人研究结论一致[4~5, 9]。图4表明3种结构的弥散系数均随着流量升高基本保持不变,弥散度随着流量升高逐渐降低。理论上,弥散系数随着流量升高应该逐渐增大[4~5, 25]。但本文中弥散系数变化趋势不明显,Dewaide等[7]和Zhao等[9]认为这可能是流量变化范围较小造成的。但本文最大流量和最小流量差距明显,或许不是这个原因,可能是计算方法不合理导致的。弥散度与流量呈负相关,与前人研究结果一致[4~5, 9]。
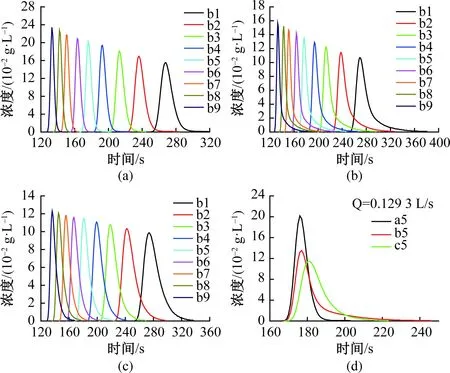
图3 不同流量条件下的穿透曲线Fig.3 Breakthrough curves under different flow conditions

表2 穿透曲线特征参数和溶质运移参数Table 2 Morphological parameters of the BTCs and transport parameters
图3d为3种管道结构穿透曲线的对比,不同流量的曲线对比规律相同,在此只列出流量5的曲线。可以看出水箱与单管相比,峰值浓度明显较低,拖尾较长。与对称水箱相比,不对称水箱峰值浓度较低,拖尾较短。3种管道结构间的弥散系数和弥散度的大小关系均为不对称水箱>对称水箱>单管(图4),结论与文[8~9]的研究结论一致。相比单管,水箱的峰值浓度较低,拖尾较长,说明水箱的瞬态存储导致溶质运移滞后。对称水箱峰值浓度相比单管下降的主要原因是部分溶质瞬态存储在水箱两侧漩涡内而导致前缘穿透的溶质质量减少。而不对称水箱峰值浓度相比单管下降原因为:(1)主体溶质在不对称水箱内充分混合导致溶质羽分布更均匀,(2)部分溶质在水箱内的瞬态存储导致前缘穿透的溶质质量减少。相比对称水箱,不对称水箱内漩涡较剧烈,导致溶质羽分布较均匀,同时瞬态存储在水箱内的溶质能较快流出水箱,这可能是导致峰值浓度较低以及拖尾较短的原因[8~9]。
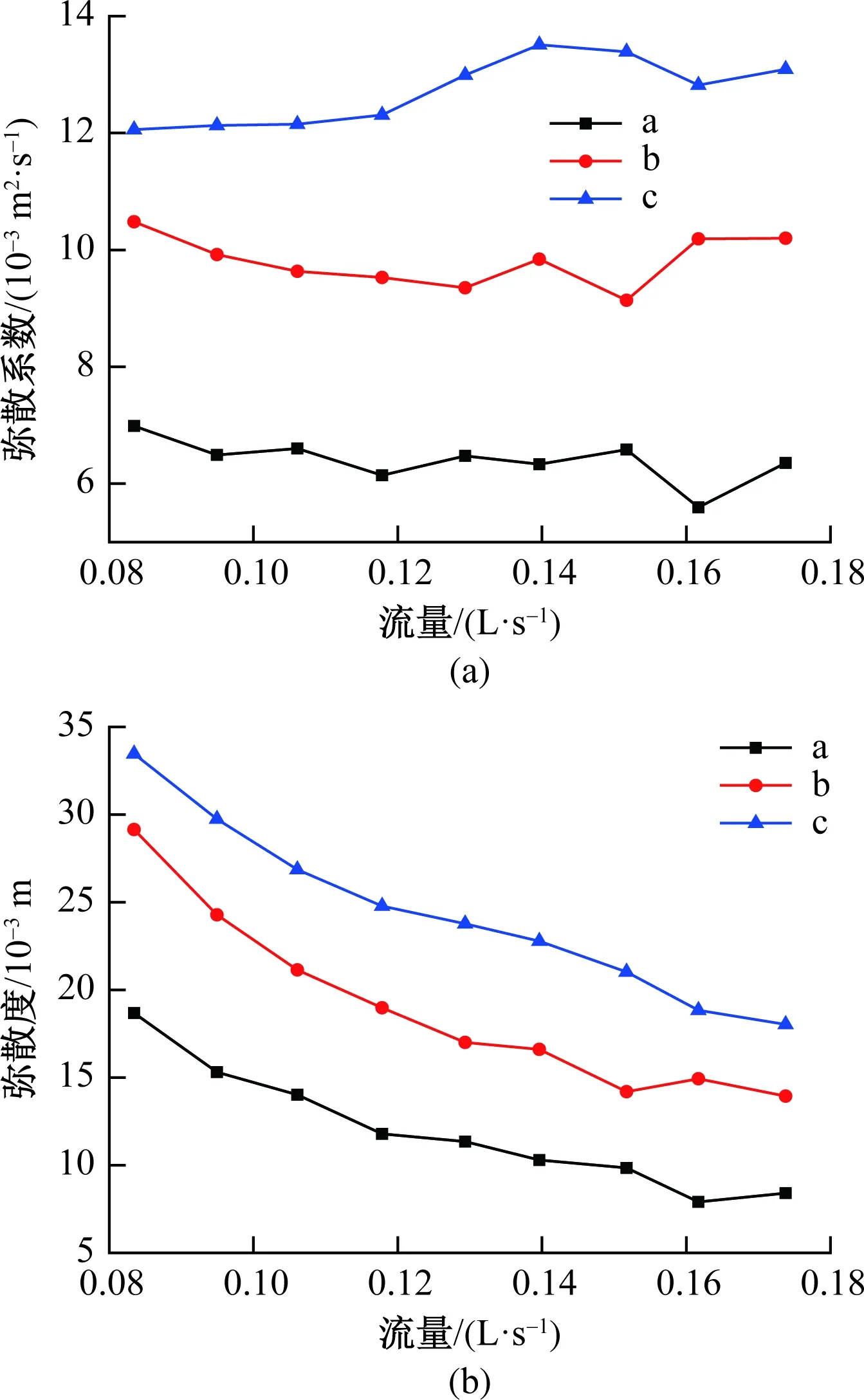
图4 弥散系数和弥散度随流量的变化Fig.4 Changes in dispersion and dispersivity with flow rate
4 穿透曲线特征参数预测和对比
穿透曲线(BTC)特征参数(Cp,tp,t1,t2,t0.5r,t0.5f,t0.1f)对于溶质运移的研究十分关键[3],这其中,峰值浓度、峰值时间、示踪剂首次检出时间和最后检出时间尤为重要[24, 26]。Field[14]指出,在岩溶管道污染物运移研究中,示踪剂最先到达时间可能比平均运移时间更有价值,示踪剂最后检出时间同样也很重要。示踪剂最后检出时间严格受控于检出限、监测时长和分辨率,因此很难确定[27]。本文取溶液电导率降低至比水的背景值高1 μS/cm的时刻为观测结束时间。
RTD曲线和单位-响应曲线曾被用来建立相应参数间的特征关系[3]。本文按照流量由小到大进行编号1-9,对流量编号2-8的数据进行统计分析,拟合得到峰值时间与其他BTC特征参数以及BTC特征参数与流量间的关系式,分析参数随流量升高的变化规律。提出两种方法对最小和最大流量条件下的BTC特征参数(峰值浓度、运移时间)进行预测,和实测值进行对比,判断预测效果。两种预测方法的共同点是:拟合得到峰值时间与流量的关系式,根据已知流量预测峰值时间。
4.1 峰值时间预测
优势流速(vp)与流量(Q)之间的关系常满足以下表达式[3, 24]:
vp=kQa
(2)
根据tp=x/vp推导出峰值时间(tp)与Q之间的关系符合以下表达式:
(3)
式中:k,a——系数。
构建tp与Q的特征关系,见图5,其中三种管道结构的拟合度(R2)均大于0.999,表明拟合表达式能较好表征tp与Q的关系。可根据该表达式由Q预测tp。相比单管和对称水箱,溶质在不对称水箱内的运移路径较长[8],导致溶质流经不对称水箱时消耗更长时间,峰值浓度到达管道出口比较滞后,因此不对称水箱的关系式与单管和对称水箱的关系式明显不同。
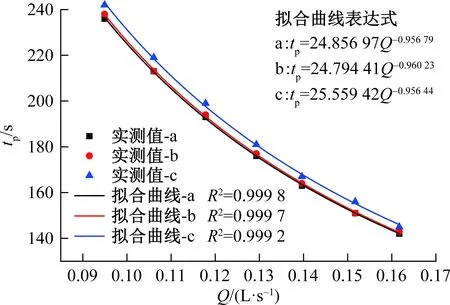
图5 峰值时间与流量的关系Fig.5 Relationship between the travel time of the peak concentration (tp) and the flow rate (Q)
4.2 峰值浓度和其他运移时间预测
采用两种方法对峰值浓度和其他运移时间进行预测。预测方法1:根据已知流量预测得到峰值时间,然后拟合其他参数与峰值时间的关系式[3],通过峰值时间预测得到其他参数。预测方法2:分别拟合不同参数与流量间的关系表达式,根据流量预测得到对应的参数值。通过两种方法获得的预测结果见表3。
4.2.1预测方法1
(1)峰值浓度与峰值时间的关系
单位-响应曲线的峰值浓度(Cup)随峰值时间(tp)的衰减变化关系式为[3, 24, 28]:
(4)
式中:α,β——拟合得到的系数。
从而推导出:
(5)
本实验中回收质量Mr随着峰值时间的变化几乎不变,近似为常数,因此Cp与tp的关系可通过乘幂表达式进行表征,见图6,拟合度(R2)接近或大于0.99,总体拟合较充分,可根据该表达式和预测的峰值时间得到峰值浓度。

图6 峰值浓度与峰值时间的关系Fig.6 Relationship between the peak concentration (Cp) and the travel time of the peak concentration (tp)
(2)其他运移时间与峰值时间的关系
示踪剂首次检出时间(t1)与峰值时间(tp)的关系符合线性表达式[3, 24]:
t1=btp
(6)
式中:b——拟合得到的斜率系数。
图7a表明t1和tp的关系紧密,可以有效地通过tp对t1进行预测。反之,一旦知道t1,可以预测tp。图7b为示踪剂观测结束时间(t2)与峰值时间(tp)的特征关系,其中三种结构的R2均大于0.99,表明线性表达式能较好表征t2和tp的关系,可由tp预测t2。
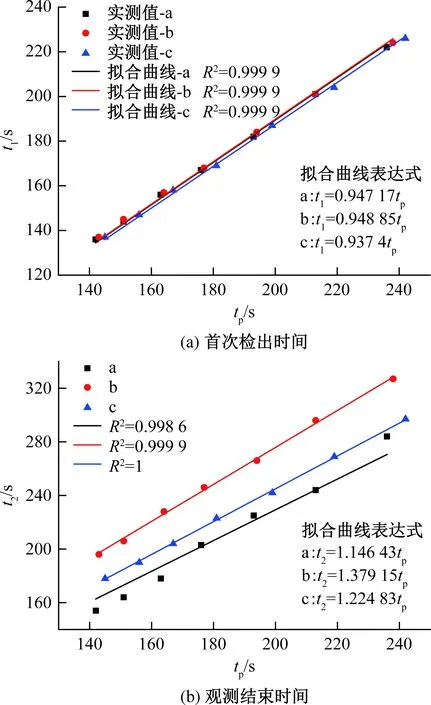
图7 示踪剂首次检出时间和观测结束时间与峰值时间的关系Fig.7 Relationship between the travel time of leading edge (t1) and trailing edge (t2) and the peak time (tp)
构建t0.5r,t0.5f,t0.1f,tbar与tp之间的特征关系,拟合得到的线性表达式和关系曲线,见图8。三种结构的R2都大于0.999,说明运移时间与峰值时间之间的线性关系密切,可根据表达式和峰值时间有效预测运移时间。

图8 运移时间和峰值时间的关系Fig.8 Relationships between other travel time and the travel time of the peak concentration (tp)
4.2.2预测方法2
(1)峰值浓度与流量的关系
根据式(3)和式(4)可知单位峰值浓度(Cup)与流量(Q)的关系符合如下表达式:
Cup=αx-βkβQaβ
(7)
峰值浓度(Cp)与流量(Q)的关系式如下:
(8)

图9 峰值浓度与流量的关系Fig.9 Relationship between the peak concentration (Cp) and the flow rate (Q)
本实验中回收质量Mr可看做常数,因此Cp-Q应该符合乘幂关系。图9为拟合得到的Cp与Q的关系表达式。三种结构的R2都接近或大于0.99,拟合效果较好,表达式能较好表征Cp与Q的关系,可通过流量预测峰值浓度。
图9显示,三种结构的峰值浓度均随流量的升高而逐渐增大;单管峰值浓度随流量的升高而增加的速度最快,不对称水箱峰值浓度随流量的升高而增加的速度最慢。Göppert等[6]和赵小二等[8]讨论了流量大小对峰值浓度的影响,指出流量增大增强了对溶质的稀释,降低峰值浓度;流速增加缩短了弥散作用时间,增大峰值浓度。峰值浓度随着流量升高而增大,表明流量稀释作用对峰值浓度的影响小于弥散时间缩短对峰值浓度的影响。相比单管和对称水箱,水流流经不对称水箱时形成较剧烈漩涡,溶质云在漩涡的作用下更充分地混合导致流量增加对溶质的稀释作用较强,减缓了峰值浓度的上升。
(2)运移时间与流量的关系
t1与tp之间符合线性关系,由式(3)和式(6)可知,t1与Q的关系符合如下乘幂形式:
(9)
图10为拟合得到的t1-Q与t2-Q关系曲线和表达式,三种结构的R2均大于0.99,表明表达式能较好表征t1,t2与Q之间的关系,可根据Q,预测得到t1和t2。同t1,t2一样,t0.5r,t0.5f,t0.1f,tbar与Q间的关系也符合乘幂方程式,如图11所示。三种结构的R2都大于0.999,拟合效果较好,可根据表达式预测得到四种运移时间。
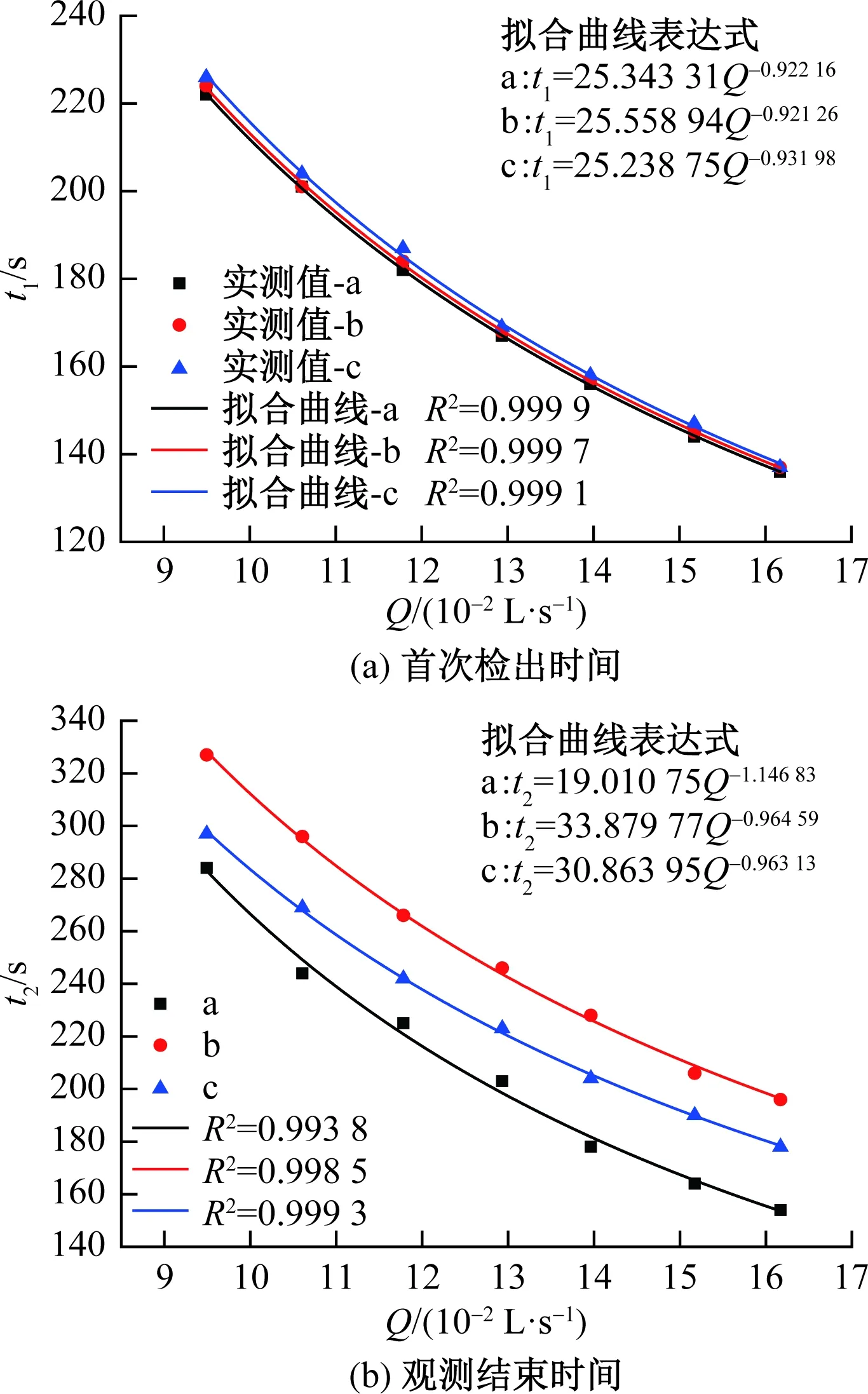
图10 示踪剂首次检出时间和观测结束时间与流量的关系Fig.10 Relationship between the travel time of leading edge (t1) and trailing edge (t2) and the flow rate (Q)
图10显示三种结构的t1几乎相同,说明水箱对t1的影响较小,三种结构的t2大小关系为对称水箱>不对称水箱>单管,是拖尾长度的不同导致的。对称水箱的t1,t0.5r,tp,t0.5f的大小与单管相比都没有明显不同,但t0.1f,t2明显较大(图10和11),说明对称水箱对穿透曲线形态的影响主要体现在拖尾曲线段。不对称水箱的整条穿透曲线(t0.5r,tp,t0.5f,t0.1f,t2)相比单管都明显滞后,且随着时间的推移,不对称水箱和单管运移时间的差别越来越大,说明不对称水箱影响了整个溶质云的运移时间。溶质流经对称水箱时受到的干扰,主要体现在部分溶质在主管道两侧漩涡内的滞留存储,而主体溶质经过对称水箱的优势通道流出,和流经单管类似。不对称水箱内的水流漩涡相比对称水箱明显不同,水流经不对称水箱时,除了少量溶质在漩涡内瞬态存储导致曲线拖尾之外,主体溶质在不对称水箱内由于运移路径较长而滞后穿透出管道。两种水箱的平均运移时间明显大于单管,直观表明了水箱导致溶质运移滞后;两种水箱的平均运移时间几乎相同,具体什么原因需要进一步研究。很显然,几种运移时间随着流量增大均呈下降趋势,幂律系数接近负1,说明运移时间和流量的关系近似为反比关系。
4.3 两种方法预测结果对比
从表3可以看出,大多数情况下,方法2的预测相对误差小于方法1,预测结果更接近实测值,说明本实验条件下,方法2的预测效果较好。但在野外岩溶地区,降雨或蒸发等因素常导致流量条件控制不够严格[3],在一次示踪实验中流量可能是变化的,这时BTC特征参数随着流量的变化关系或许不能通过表达式很好地拟合。这种情况下,则不能通过方法2进行预测,而由于峰值时间受到流量波动的干扰相比其他参数较小,采用方法1进行预测或许更好,先根据流量预测峰值时间,再通过峰值时间预测其他。
5 结论
(1)随着流量升高,穿透曲线峰值浓度逐渐增大,曲线拖尾逐渐缩短,弥散系数基本不变,弥散度逐渐下降。单管峰值浓度随流量升高增加的速度最快,不对称水箱峰值浓度随流量升高增加的速度最慢。相比不对称水箱,对称水箱峰值浓度较大,拖尾较长。对称水箱导致部分溶质瞬态存储在漩涡中明显滞后,不对称水箱导致主体溶质滞后穿透以及少部分溶质瞬态存储在漩涡中滞后运移,但两种水箱的平均运移时间几乎一致。
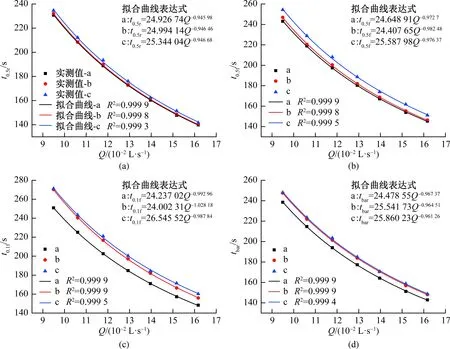
图11 运移时间和流量的关系Fig.11 Relationships between the travel time and the flow rate (Q)
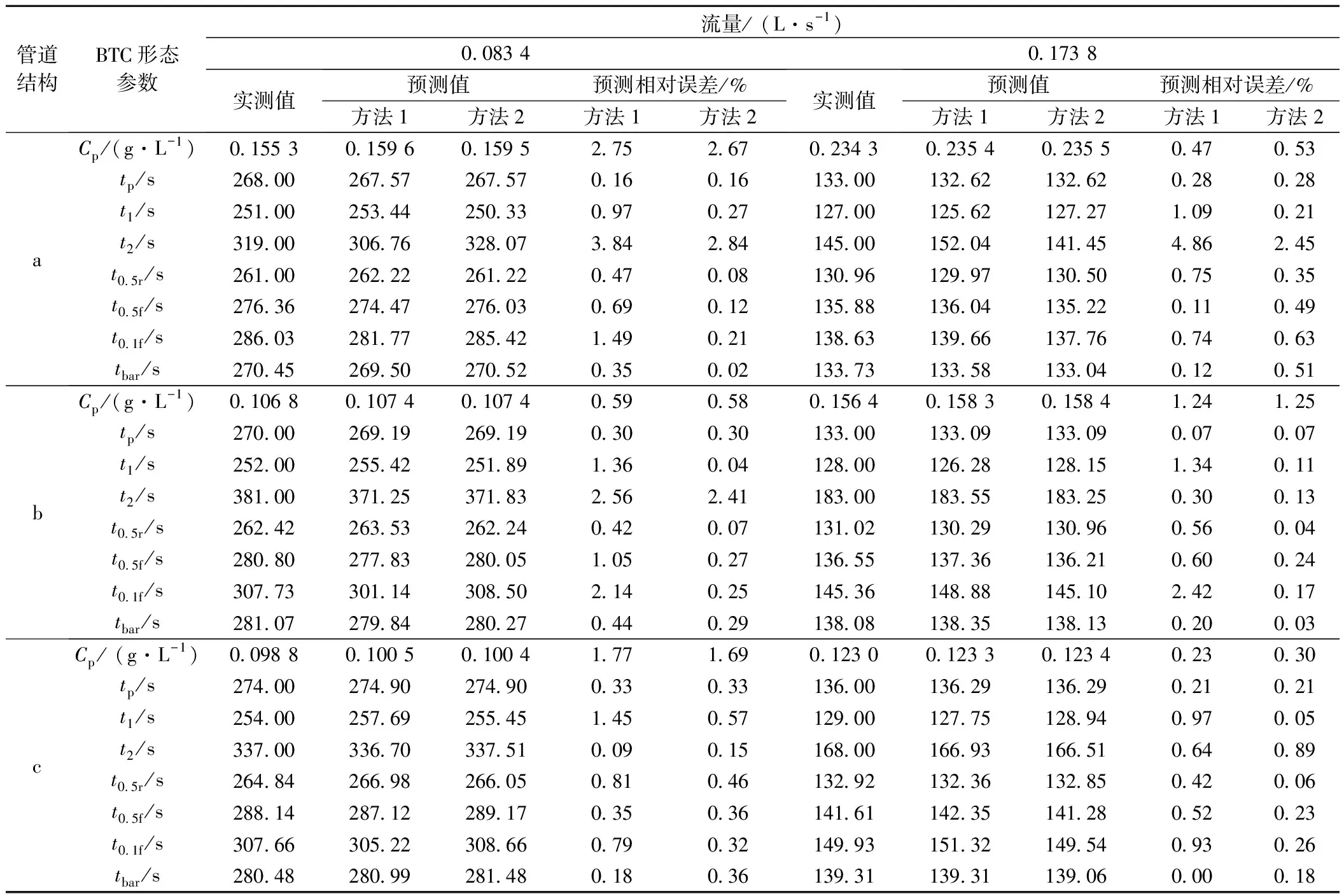
表3 预测结果Table 3 Prediction results
(2)乘幂表达式能较好表征穿透曲线特征参数与流量的关系,乘幂表达式也能较好表征峰值浓度与峰值时间的关系,线性表达式能较好表征其他运移时间与峰值时间的关系。
(3)在本实验中,相比先通过流量预测峰值时间,再预测峰值浓度和其他运移时间这种预测方法,直接根据流量预测穿透曲线特征参数的方法能取得更好的预测效果,但在野外条件下,前者或许更可取。本文对特征参数进行预测,可以对穿透曲线的形状有一个初步的判断,接下来可尝试建立溶质运移模型参数与流量的关系,通过预测的运移参数正演获得完整的穿透曲线。

