单排四点接触球转盘轴承承载能力研究

刘荣，李玉川，刘静 ，王华

(1.南京工业大学 机械与动力工程学院，南京 211816；2. 洛阳LYC轴承有限公司，河南 洛阳 471039)

转盘轴承是风力发电机、塔式起重机等旋转设备中的关键部件，套圈带有传动齿，与驱动小齿轮啮合传递扭矩[1]，可以同时承受轴向力(Fa)、径向力(Fr)和倾覆力矩(M)的作用。转盘轴承在使用过程中会发生各种故障[2]，静承载能力是检验转盘轴承的主要指标。相比普通轴承，转盘轴承尺寸较大且工作状态为低速重载，所以传统应用于普通轴承的计算方法往往不适合转盘轴承。

为设计出高承载能力和高可靠性的转盘轴承，分析圆周载荷分布在转盘轴承设计计算中是必不可少的。近年来，随着数值计算技术的发展，轴承滚道载荷分布计算中繁琐的计算过程可以由计算机完成，有限元方法得以广泛应用。文献[3-4]采用8结点3D六面体实体单元建立转盘轴承整体模型，但转盘轴承接触对多，采用该方法建模难度大且不易收敛。文献[5]将每个接触对由4个刚性壳单元、8个刚性杆单元和2个非线性弹簧单元代替，建立转盘轴承支承简化模型，但该方法建模难度较大。文献[6]将超单元技术应用到上述简化模型中，在不降低计算精度的前提下，提高了计算效率。文献[7]通过将滚子滚道的非线性接触等效为非线性弹簧单元, 对六排滚子转盘轴承进行了有限元强度校核。文献[8]采用非线性弹簧代替圆柱滚子-滚道接触的有限元仿真模型，计算得到转盘轴承内部接触载荷分布。文献[9]采用非线性弹簧替代钢球与沟道的接触,梁单元替代轮毂与变桨轴承以及叶片与变桨轴承之间的安装螺栓,建立有限元模型,计算风电变桨转盘轴承的载荷分布。

现采用非线性弹簧模拟沟道与钢球之间的接触，利用ABAQUS有限元软件分析转盘轴承沟道的载荷分布。为验证仿真结果的可靠性，利用自主开发的转盘轴承综合性能试验台进行试验，并与仿真结果对比分析，研究转盘轴承承载特点和误差来源。

1 有限元分析

1.1 非线性弹簧模拟钢球沟道接触行为

以沟道中心直径1 m的外齿式单排四点接触球转盘轴承(010.40.1000)为研究对象，其截面示意图如图1所示。图中：Pr为截面间隙；Dw为钢球直径；h，a分别为曲率中心的水平偏心距和垂直偏心距；α0为接触角。单排四点接触球式转盘轴承的沟道一般由4个相同的圆弧沟道组成，Cid，Ced，Ciu，Ceu分别为套圈沟道截面的沟曲率中心(下标 i，e分别表示内、外圈；u，d分别表示上、下沟道)。沟曲率半径系数f按(1)式计算，根据实际生产中厂家的意见反馈以及相关资料，内、外圈沟道沟曲率半径系数均为0.525。

图1 转盘轴承截面图Fig.1 Cross section for slewing bearing

(1)

式中：R为沟道的沟曲率半径。

在单排四点接触球转盘轴承中，外载荷作用下，沟道挤压钢球形成接触副。根据Hertz接触理论，钢球与沟道间接触力与接触变形的关系为[10]

(2)

式中：Q为接触载荷；K为接触刚度,可通过Hertz接触理论解析获得[10]483；δ为上、下沟道与钢球的总接触变形。

由(2)式可知，沟道与钢球之间的载荷-变形关系是非线性的，为简化模型，采用非线性弹簧代替沟道-钢球接触行为，只要保证非线性弹簧与沟道-钢球之间的载荷-变形关系一致即可，每个钢球由一对非线性弹簧代替，如图2所示，非线性弹簧PeuPid代替CeuCid方向的接触对，PiuPed代替CiuCed方向的接触对。

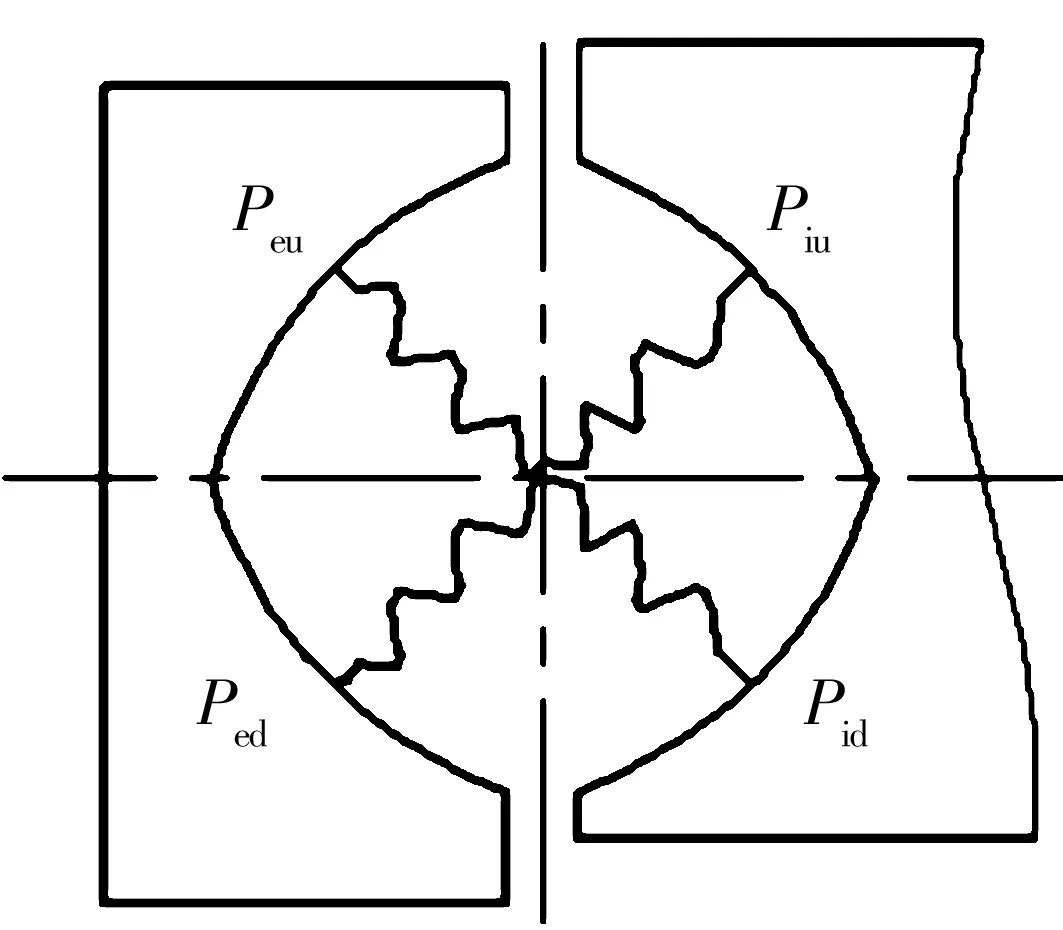
图2 非线性弹簧模拟钢球Fig.2 Nonlinear spring instead of steel ball

非线性弹簧的载荷-变形关系为

F=KsΔ，

(3)

式中：F为作用力；Ks为弹簧弹性系数；Δ为变形量。

当满足Δ=δ，F=Q时,有

Ks=2-(3/2)KΔ1/2。

(4)

钢球仅受到压力作用时与沟道发生接触，故非线性弹簧仅受压力作用，当受到拉力作用时无刚度，非线性弹簧载荷-变形特性如图3所示。

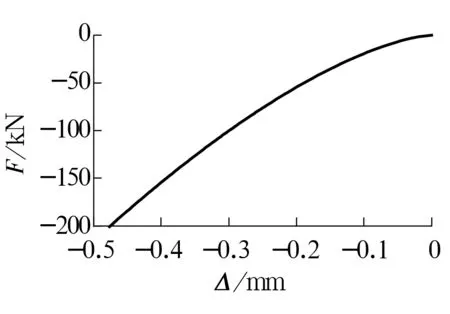
图3 非线性弹簧载荷-变形曲线Fig.3 Load-deformation curve of nonlinear spring

弹簧的初始长度为

L=Dw+2Pr。

(5)

1.2 转盘轴承有限元模型

采用非线性弹簧模拟钢球，为减小计算误差，弹簧的分布位置应与钢球保持一致，总共69对弹簧。在ABAQUS中的Interaction接触功能模块中，使用弹簧/阻尼器菜单工具，选取两点连接方式创建线性弹簧，弹簧的连接端点对应钢球与沟道的接触点，并编辑图3中载荷的变形特性。转盘轴承有限元模型及钢球编号如图4所示。

图4 转盘轴承有限元模型Fig.4 Finite element model of slewing bearing

建模过程中，在内圈、安装基础的结合面与参考点RP-inner ring之间建立运动耦合，在外圈、安装基础的结合面与RP-outer ring之间建立运动耦合，载荷(Fa=91.5kN,M=215.6kN·m)施加在参考点RP-outer ring上，内圈与安装基础的结合面施加完全固定约束，外圈与安装基础的结合面释放轴向力和倾覆力矩方向的自由度，约束其他方向的自由度，模型采用8节点六面体减缩积分(C3D8R)网格单元(图5)。

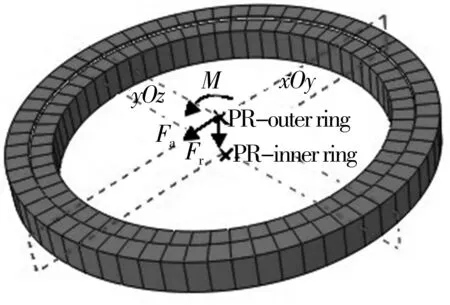
图5 网格划分Fig.5 Meshing

1.3 仿真结果

提取转盘轴承的位移云图如图6所示，从图中可以看出，在外载荷的作用下，外圈出现了沿轴向力方向的位移和沿倾覆力矩方向的转角变化。提取每根弹簧的受力情况，沟道的接触压力分布如图7所示，其中，PeuPid为CeuCid方向上布置的弹簧受到的压力；PiuPed为CiuCed方向上布置的弹簧受到的压力。由图7可知，沟道最大接触压力为236 65 N，位于35#钢球。

图6 转盘轴承变形云图Fig.6 Deformation nephogram of slewing bearing

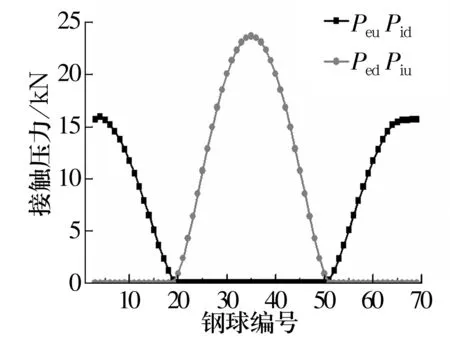
图7 非线性弹簧受力曲线Fig.7 Load curves of nonlinear springs

2 载荷分布试验

为验证有限元仿真结果与实际工程中转盘轴承的载荷分布情况的一致性，利用实验室自主开发的转盘轴承试验台进行转盘轴承静力试验。

2.1 试验方法

转盘轴承钢球与沟道的接触载荷值无法直接测得，在轴承圆周内侧布置钢结构应变片，采用DH3815N-3静态应变测试系统进行应变测试，间接得到转盘轴承的载荷分布。室温下进行3次加载试验(载荷与仿真分析相同)，试验台如图8所示。

试验前，采用加速试验方法让钢球、隔离块及润滑脂快速磨合以达到正常的工作状态，通过控制液压油缸G1和G2的输出压力，施加与仿真分析中相同的轴向力和倾覆力矩，选取的载荷值均低于转盘轴承的极限载荷。

在转盘轴承内圈内侧的圆周方向上均匀粘贴69个钢结构箔式应变片，应变测点布置如图9所示，应变片变形方向与转盘轴承的轴向方向一致，测量时均进行温度补偿。但在实际操作中，由于油嘴、铭牌等零部件的存在，应变片无法等间距布置，实际测点布置如图10所示。

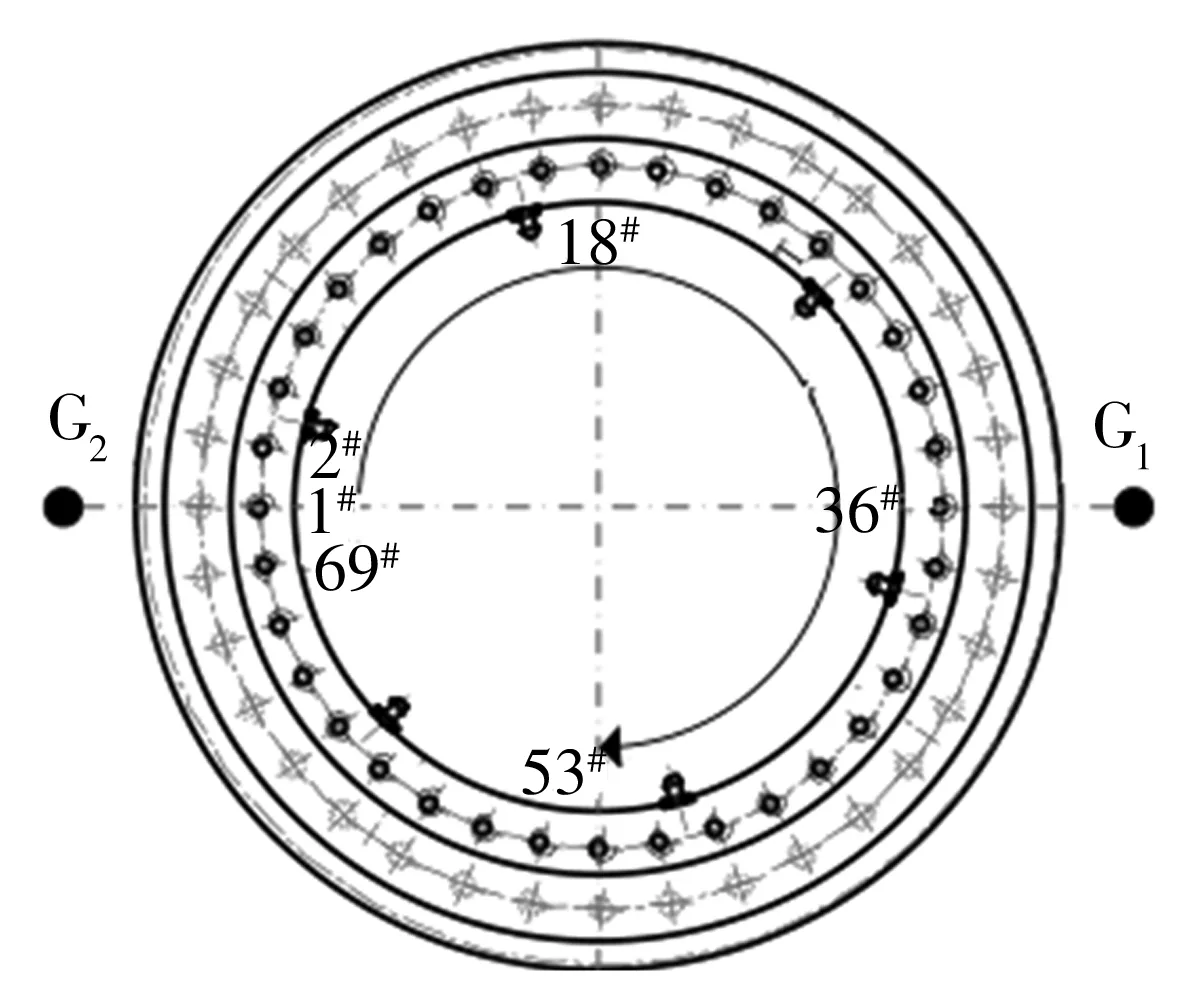
图9 应变仪测量点的布置图Fig.9 Layout diagram of strain gauge measuring points

图10 应变仪测量点的实际布置图Fig.10 Actual layout diagram of strain gauge measuring points

2.2 试验结果

1#～69#应变片的应变曲线如图11所示。从图中可以看出，3次试验中转盘轴承上应变的变化趋势基本一致。靠近G1端，即25#～48#应变片的应变为负，应变片受压；靠近G2端，即1#～6#和57#～69#应变片的应变为正，应变片受拉，且大载荷区域基本分布于25#～50#应变片之间。

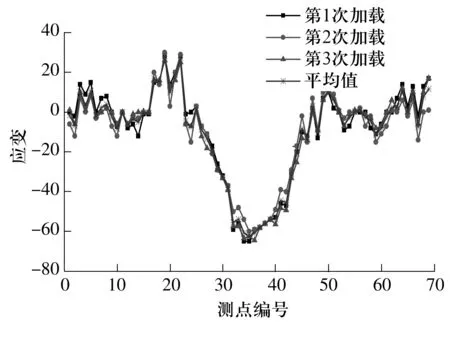
图11 试验应变曲线Fig.11 Strain curves of experiment

3 结果分析

根据应变片在转盘轴承上的粘贴位置，提取有限元模型中相应位置处钢球与沟道的接触应变，有限元模型中2根非线性弹簧代替一个钢球，故转盘轴承沟道的应变分布应同时考虑2根弹簧。试验(平均值)与仿真应变曲线对比结果如图12所示。

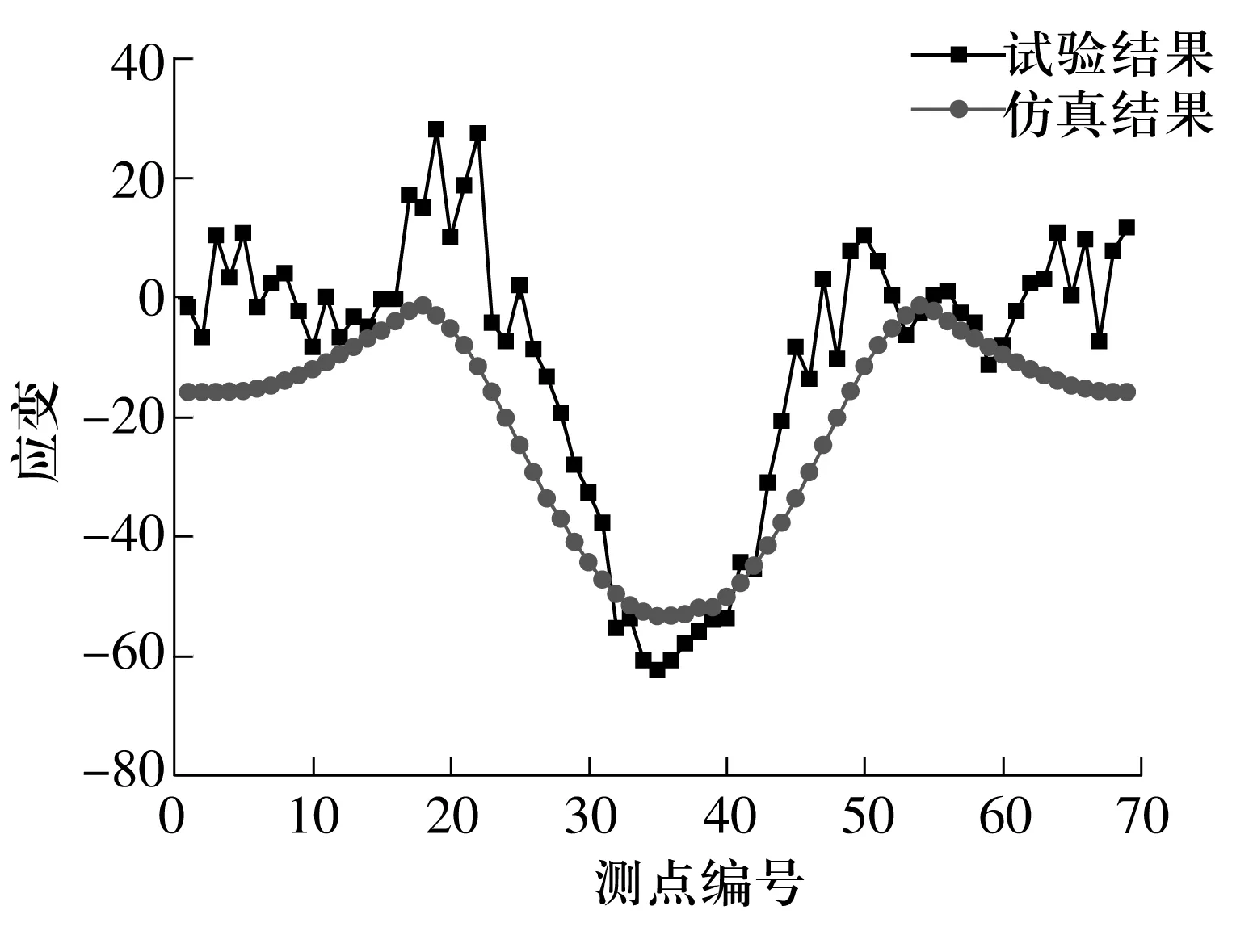
图12 试验与仿真应变曲线对比Fig.12 Comparison between experiment and simulation strain curves

从图中可以看出，试验和仿真结果中载荷分布趋势一致，其中，大载荷分布于23#～43#应变片(液压缸G1端)之间，最大载荷值均位于35#测点；次一级载荷位于1#～10#和57#～64#应变片(液压缸G2端)之间，其余位置的载荷更小。试验测得的最大应变为62.45，仿真结果为53.4，误差为14%，低于15%，可认为误差在合理范围之内[11]。

此外，15#～25#应变片受到拉力作用，试验与仿真结果的误差较大，一方面是试验设备引起的误差，包括液压缸加载、应变片粘贴、应变补偿等；另一方面,由于在实际中会受到安装基础面的不平度、螺栓预紧力等因素的影响，试验中所得载荷分布与理论分析结果会有所差异，但载荷的分布区域及其变化趋势一致，由此可证明有限元分析结果的可靠性。

4 结束语

采用非线性弹簧模拟转盘轴承钢球与沟道接触的有限元简化方法，通过有限元静力分析，得到了转盘轴承沟道的载荷分布，计算时间短且效率高。通过静力加载试验获得了实际工程中转盘轴承沟道的应变分布，结果表明，仿真结果与实际载荷分布变化趋势一致，证明了有限元分析的可靠性。此外，靠近液压缸加载区为大载荷分布区。沟道载荷分布情况为转盘轴承设计计算提供了重要的依据。