基于滚动体实体模型及子结构技术的转盘轴承有限元分析

刘菁，董汉杰，汪洪，王媛媛

(1. 洛阳LYC轴承有限公司 技术中心，河南 洛阳 471039；2. 航空精密轴承国家重点实验室，河南 洛阳 471039)

转盘轴承通常尺寸较大，滚动体数量多,滚动体与内、外圈接触时接触对数量大。有限元分析中接触分析是一种高度非线性计算问题，当接触对数量较大时会给计算收敛性带来困难。滚动轴承零件间的接触行为发生在极小区域内，为提高计算精度会对网格进行细化，然而过细的网格又会使计算量急剧膨胀而超出计算机的计算能力。因此，目前对大尺寸轴承进行有限元分析时，很少进行轴承整体结构分析，往往对少量滚动体进行接触分析。即使做轴承整体有限元分析，为避免接触收敛困难，多数对其进行简化，例如采用弹簧单元模拟滚动体[1-3]，该建模方法避免了接触分析收敛困难的难题，但计算精度难以保证。鉴于此，以某三排滚子转盘轴承为例进行分析，所有滚动体采用实体六面体单元，为降低计算量，采用子结构分析技术，将三排圆柱滚子组成一个子结构，仅保留接触位置节点，对其余节点进行缩聚，建立子结构模型对转盘轴承进行有限元分析。

1 有限元分析模型

某三排滚子转盘轴承结构如图1所示。轴承在运行过程中主要受轴向力、径向力及倾覆力矩，其所承受的极限载荷见表1，最大工作载荷是指正常工作条件下允许的最大载荷，灾难性载荷是指极恶劣天气条件下承受的最大冲击载荷。

表1 极限载荷Tab.1 Limit load

图1 三排滚子转盘轴承结构图Fig.1 Structure diagram of three row roller slewing bearing

1.1 三排圆柱滚子组子结构模型

子结构分析技术又称为节点缩聚技术，将子结构节点分为外部节点(其与外部结构的节点发生直接连接或接触)和内部节点(这些节点不与外部节点发生直接联系)。通常内部节点数量远远大于外部节点数量，以本次计算为例，三组滚子总的节点数为267万个，外部接触节点数仅为12万个，内部节点数是外部节点数的22倍。在进行轴承整体模型计算时，仅子结构的外部节点参与整体刚度矩阵生成，这样可大幅提高计算效率。

文献[4-5]介绍了子结构分析技术以及子结构的刚度矩阵和载荷列阵的计算方法，在此仅对子结构分析技术的数学原理进行简述：将子结构节点按外部和内部节点分组，形成待求解的相应的外部和内部节点位移向量列阵re和ri。同时对已知的子结构刚度矩阵K和载荷列阵R也做相应分组，得出矩阵方程为

(1)

式中：Re，Ri分别为外部、内部节点载荷列阵；l为内部节点自由度个数；c为外部节点自由度个数；l，c用于下标时表示矩阵的行数和列数，如Kcl代表c行l列的刚度矩阵。

由(1)式可求出内部节点位移

(2)

再将(2)式代入(1)式得

(3)

基于子结构分析技术的三排滚子转盘轴承整体分析计算模型的计算步骤为：1)建立三排滚子三维模型(图2)；2)在模型中声明外部节点集并导出模型文件；3)对模型文件进行节点缩聚计算，生成关于外部节点的缩聚刚度矩阵及根据外部节点位移求解内部节点位移的变换矩阵；4)建立轴承整体分析的三维模型，其中包含内圈、外圈、螺栓及配合件；5)在与滚子子结构外部节点的相同位置生成相同数量的节点，并以此为基础生成接触面，每组滚子均生成2个接触面，分别与内、外圈滚道接触(图3)；6)指定6组滚子接触面与内、外圈滚道的接触关系；7)导入滚子子结构缩聚刚度矩阵，系统自动建立主模型节点与子结构外部节点的耦合关系；8)求解轴承整体有限元分析主模型；9)利用主模型求得三排滚子子结构外部节点的位移，再求出子结构中内部节点位移及其他待求参数。

图2 三排滚子组子结构有限元分析模型Fig.2 Finite element analysis model of three row roller set sub structure

图3 轴承整体分析时三排滚子组模型Fig.3 Three row roller set model for overall analysis of bearing

1.2 轴承整体有限元分析计算模型

轴承整体有限元分析模型如图4所示，轴承网格划分如图5所示，模型由内、外圈及三排圆柱滚子的外部节点构成。图5中原滚子所在位置不存在滚子实体单元，而仅存在滚子与滚道发生接触的外部节点及其构成的接触面。由于对称性，仅建立轴承半圈模型，并在剖切面上施加对称约束，即令剖切面上节点的法向位移等于0。 在轴承中心建立参考点，建立此参考点与轴承受载面的刚性耦合关系，所有外载荷(轴向力、径向力和倾覆力矩)均加载到此参考点上,同时对该参考点施加对称约束。在外圈下端面节点施加固定约束。

图4 轴承整体有限元分析模型Fig.4 Overall finite element analysis model for bearing

1.3 子结构中滚子建模

为确保有限元分析的精度，分析时对滚子采用全实体六面体单元。为避免滚子在分析中产生刚体位移，对每个滚子均使用4组低刚度系数的弹簧单元限制其沿3个方向的平动及转动。单个滚子模型如图6所示，生成子结构缩聚刚度矩阵的三排滚子模型如图2所示。

图6 单个滚子有限元模型Fig.6 Finite element model for single roller

1.4 子模型的创建

三排滚子转盘轴承内、外圈2个承重环形梁的根部是最易发生断裂的部位,由于整体分析时单元无法过度细化，造成整体分析得到的根部应力不准确。为此，必须采用子模型技术对梁的根部进行详细分析,在轴承受载最大的危险部位切出子模型，网格划分细化。内、外圈子模型的受力面及侧面位移均取自整体模型的位移计算结果，对危险部位油沟进行了网格细化，创建的子模型如图7所示。

图7 子模型Fig.7 Submodels

2 结果分析

在最大载荷工况和灾难性载荷工况下,套圈位移云图如图8所示，最大载荷工况下套圈节点最大位移为2.08 mm，在内圈上；灾难性载荷工况下最大位移为7.14 mm，同样在内圈上。局部滚动体接触应力分布情况如图9所示，由图9可知：滚动体接触斑逐渐加宽，说明滚子存在偏载情况，最大接触应力发生在滚子端部，与实际情况相符。

图8 套圈位移云图Fig.8 Displacement nephograms of ring

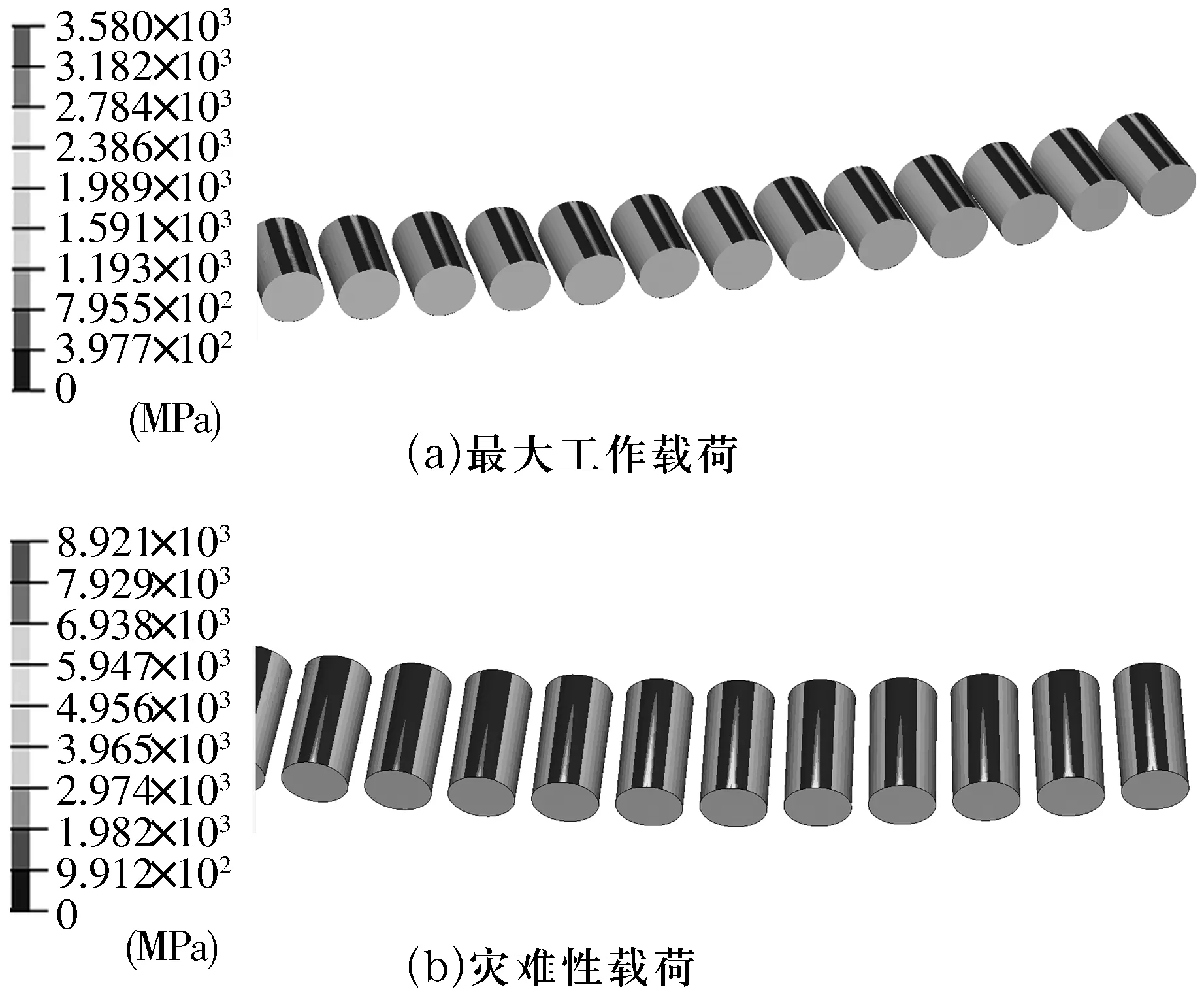
图9 局部滚动体接触应力分布Fig.9 Local contact stress distribution of rolling elemerot

运用子模型技术进行危险部位的应力计算，在灾难性载荷工况和最大工作载荷工况时套圈油沟根部应力分布图分别如图10和图11所示。由图可知：灾难性载荷工况下内圈最大应力为1 880 MPa，外圈最大应力为1 190 MPa；最大载荷工况内圈最大应力为534 MPa，外圈最大应力为338 MPa；危险部位均发生在套圈悬臂环的根部，与实际情况相符。为降低根部应力，应尽量增加根部圆角尺寸。

图10 灾难性载荷工况时套圈油沟根部应力分布图Fig.10 Stress distribution nephograms of root at oil groove of ring under catastrophic load condition

图11 最大工作载荷工况时套圈油沟根部应力分布图Fig.11 Stress distribution nephograms of root at oil groove of ring under maximum working load condition

通过以上分析可知：在最大工作载荷工况时，轴承最危险部位的最大应力(534 MPa)小于材料屈服极限(700 MPa)，最大位移(2.08 mm)也较小，满足使用要求。经实测，该计算位移与实测结果十分接近，说明建模方法是可行的。在灾难性载荷工况时，轴承最危险部位的最大应力(1 880 MPa) 远超材料的屈服极限(700 MPa)，最大位移(7.14 mm)也较大，使用存在很大风险。

3 结束语

针对转盘轴承有限元分析存在的困难和问题，提出了采用滚动体实体单元代替简化的一维单元以便有效提高计算精度的方法。为解决采用滚动体实体单元建模后有限元模型计算量大的问题，提出了采用子结构技术提高计算效率的方法，给出了子结构技术的理论依据及详细的实现步骤。并以某大尺寸三排滚子转盘轴承为例进行分析，分析结果可为大型转盘轴承的设计及分析提供参考。