结合差分阵列与幅度谱减的双麦语音增强算法

徐 娜 吴长奇

(1. 燕山大学信息科学与工程学院，河北秦皇岛 066004；2. 河北省信息传输与信号处理重点实验室，河北秦皇岛 066004)

1 引言

麦克风阵列语音增强由于引入了空域信息，能够更好的抑制方向性噪声干扰，取得更好的增强效果。通常随着麦克风数量的增加，往往能够获得更好的噪声抑制性能。但是大多数基于麦克风阵列的语音增强算法由于阵列尺寸、麦克风数量、运算速度等限制并不能用于诸如助听器之类的小型设备。考虑到这些因素，双麦克风阵列则在算法性能与可应用性两方面做到了平衡，常用于小型设备[1-2]。

差分麦克阵列(Differential microphone arrays, DMAs)具有超强方向性，体积小并且其波束模式几乎是频率不变，这使得即使在强混响和噪声环境下也能得到高可懂度的语音信号[3- 4]，适合用于小型设备。

经过差分阵列处理后能对噪声进行一定的抑制，但是仍会有残留噪声，且噪声源跟声源越接近，则残留噪声越多。文献[5]提出了一种算法，该算法将一阶差分麦克风阵列技术与谱减法相结合，利用静音段和参考噪声对语音通道中的噪声进行估计，并进行谱减，与普遍采用的自适应零限波束形成技术相比有明显的信噪比改善。但该算法依赖于对静音段的估计，当对测试语料静音段估计不准时，该算法会对语音造成一定损伤，算法整体的鲁棒性不高。文献[6]提出了一种基于相关函数的双麦克语音增强算法，该算法首先利用两输入信号相关函数的实部与虚部对输入信噪比进行估计，然后利用估计的信噪比构造维纳滤波增益函数，进行后置滤波。该方法避免了对静音段的估计，与已有的波束形成算法相比，在语音可懂度上有明显提高，适用于助听器设备。文献[7]在此基础上对噪声模型进行了改进，但两者依旧是利用相关函数来对估计信噪比，并没有将两麦克构成的差分阵列优势充分利用起来。

本文算法首先利用一阶差分阵列技术，对两麦克风采集到的带噪语音信号进行处理，得到语音通道信号和噪声通道信号。接着对语音通道信号和噪声通道信号进行理论推导与数学分析。参考利用相关函数进行信噪比求解的方法，利用两通道信号构造方程，求解语音通道信号的信噪比。然后将求得的信噪比用于幅度谱减法，实现对残留噪声的消除。针对语音通道信号信噪比求解方程的构造，本文给出了两种不同计算方法。本文所提算法既利用了阵列的空间滤波特性来处理方向性的噪声干扰，又借助传统的谱增强技术实现了进一步语音增强。最后通过仿真实验，对本文算法的性能进行了评价，并与其他算法进行了比较。

2 双通道信号模型

假设远场声源信号在自由场中以平面波的形式传播，声音到达2个麦克风的传播模型[8]如图1所示。

假设目标声源来自端射方向即0°方向，噪声来自θ方向。以第一个麦克风作为参考麦克，则两麦克风接收到的信号可表示为：

y1(k)=x(k)+ν(k)

(1)

y2(k)=x(k-τ0)+ν(k-τ0cosθ)

(2)

式中k为离散时间单位，x(k)为目标信号，ν(k)为干扰信号，δ为两麦克风之间的间距，τ0=δ/c*fs为目标声源在端射方向时两麦克风间的时延，fs为信号采样频率，c为声速(c=340 m/s)，在差分阵列中有δ≪λ(λ为声学波长)。

将式(1)和式(2)中的时域离散信号加窗分帧处理后转换到短时离散傅里叶变换域表示，可得：

Y1(ωl,m)=X(ωl,m)+V(ωl,m)

(3)

Y2(ωl,m)=e-jωτ0X(ωl,m)+e-jωτ0cos θV(ωl,m)

(4)

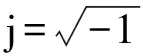
3 算法描述

3.1 一阶差分阵列

为了抑制干扰噪声V(ωl,m)，首先设计两个一阶心形差分阵列，形成声源入射方向即0°方向增益为1，180°方向的增益为0的前向心形波束和0°方向增益为0，180°方向增益为1的后向心形波束，对两麦克风采集到的带噪语音信号进行处理，实现初步语音增强。经差分阵列处理后的信号分别表示为CF(ω)和CB(ω)。

(5)

(6)

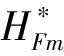
(7)

将式(3)、式(4)和式(7)分别带入式(5)和式(6)可得:

(8)

(9)

从式(8)和式(9)可以看出，经过差分阵列处理后CF(ω)中包含语音项和残留噪声项，CB(ω)中仅含噪声项，所以可以利用CF(ω)与CB(ω)对CF(ω)中的信噪比进行估计，并构造后置滤波增益G(ω)对CF(ω)中的残留噪声进行进一步消除。整体算法系统框图如图2所示。

图2 算法系统框图Fig.2 Algorithm diagram

3.2 后置滤波增益估计

本节首先对CF(ω)中的残留噪声进行了理论分析，接着利用了背对背心形波束的输出CF(ω)与CB(ω)对CF(ω)中信噪比进行估计，并给出了两种不同的计算方法。之后利用估计的信噪比构造后置滤波增益G(ω)对CF(ω)中的残留噪声进行进一步消除。

分别求CF(ω)与CB(ω)的互功率谱密度和各自的自功率谱密度，如下：

ΦVV(ω)

(10)

(11)

(12)

由式(10)可知CF(ω)中的信噪比为:

(13)

结合式(13)可得CF(ω)与CB(ω)的自功率谱比值为：

(14)

由式(14)可解出SNR(ω)即：

(15)

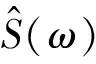
(16)

(17)

式中μ为过减因子，Gmin为最小增益。后续的实验中设置μ=1.3，Gmin=0.02。

3.2.1 信噪比估计方法1

当θ很小时有sinθ≈θ所以可做如下近似：

(18)

(19)

(20)

ΦY1Y1(ω)=ΦXX(ω)+ΦVV(ω)

(21)

图3给出了以上三个近似项与真实项之间的误差(L=256,c=340 m/s,δ=0.018 m,fs=16 kHz)，从图中可以看出对同一频率而言在120°～180°范围内误差要小，对同一角度而言，在低频区域误差要小，综合分析可以看出在1≤l≤32范围内对于所有的角度而言，整体的误差几乎为0。所以后续可以利用这些频点的信息对信噪比进行估计。

图3 真实项与近似项误差分析Fig.3 Error analysis of real item and approximate item

令：

(22)

对式(22)进行整理可得：

(M(ω)+1)cos2θ+2(1-M(ω))cosθ+

(M(ω)-3)=0

(23)

利用求根公式可以解得在1≤l≤32(l为整数)对应频点的值cosθ(ω)。

(24)

利用求根公式得到了两个解，但由于-1≤cosθ≤1，所以其中一个恒为1的解并没有实际的价值可以舍去，所以有：

(25)

为了消除估计误差，将各频点的值求平均，并利用递归的方式对每一帧的cosθ(m)进行平滑可得:

(26)

cosθ(m)=α.cosθ(m-1)+(1-α).cosθ(m)

(27)

α为平滑因子，后续试验中α取0.68，将式(27)带入式(15)可得到SNR(ω)。

3.2.2 信噪比估计方法2

方法2跟方法1的求解思路相同，只是利用了不同的功率谱来构造二次方程。

令：

(28)

对式(28)进行整理可得：

(M(ω)+1)cos2θ-2M(ω)cosθ+(M(ω)-1)=0

(29)

利用求根公式可以解得在1≤l≤32(l为整数)对应频点的值cosθ(ω)值：

(30)

同方法一，将各频点的值平均并对相邻帧进行平滑可得cosθ(m)，进而得到CF(ω)中的信噪比。

4 仿真实验与性能评价

本节通过Matlab仿真实验来验证本文所提算法的有效性,通过两个客观指标对一阶差分阵列算法(这里简称DMA算法)与本文提出的两种方法及文献[6]提出基于相干函数的算法(这里简称为Coherence算法)进行评估比较，分析其性能差异。仿真实验中两麦克风接收到的信号按照第2节给出的双通道信号模型生成(这里暂不考虑混响和反射因素)。在诸如助听器类的小型设备中，麦克风间的间距通常小于20 mm。考虑到实际应用中尺的限制，在仿真实验中将两麦克风间距δ设为0.018 m，这与文献[7]中的阵列尺寸相同。目标声源方向为阵列端射方向，方向性干扰取自Noisex92库中的Babble噪声及一段音乐(歌曲宁夏片段)，目标信号与干扰信号均假设为远场信号。采用加窗分帧的方式处理对信号进行预处理,信号采样频率为16 kHz，窗函数为汉明窗，帧长256,帧移128。最后处理完的信号经IFFT以重叠相加的方式转换到时域。

为了评估不同算法处理后语音信号的质量，这里采用主观语音质量评估[10](Perceptual Evaluation of Speech Quality, PESQ)和频率加权分段信噪比[11](frequency-weighted segmental SNR, fwsegSNR)进行评测。文献[12]指出PESQ和fwsegSNR这两个客观评估指标与语音的整体质量及语音信号损伤程度关联很大，更适合评估语音增强算法的性能。PESQ的得分在1.0到4.5之间，分值越高表示语音质量越好。本文所用到的PESQ及fwsegSNR的Matlab代码均来自文献[11]。

本文选取了文献[13]中用到的12组不同性别不同内容的纯净句子语料分别在信噪比为10 dB、-5 dB、0 dB、5 dB、10 dB的情况下进行加噪。加噪过程语音的幅度保持恒定，根据期望的信噪比来对噪声幅度进行修改。在同一组信噪比条件下，分别使用Coherence算法和DMA算法及本文提出的算法进行处理。同一信噪比下同一种类型噪声经过同一增强算法处理可以得到一种测试条件，再将这种测试条件下的12组句子的fwsegSNR和PESQ的平均值作为最终的数值。这样的测试条件共有4×5×4即80种。

图4和图5分别给出了输入信噪比取-10 dB～10 dB，噪声分别为Babble与Music，方向为120°和90°情况下四种算法得到的fwsegSNR和PESQ分值。从图4和图5可以看出，当干扰方向与目标声源方向接近时，所有算法的性能都会有所下降。本文提出的两种计算方法在所有测试条件下性能基本接近。与DMA算法相比，噪声位于90°方向时PESQ平均有0.61分提高， fwsegSNR平均有4.6 dB提升；噪声位于120°方向时PESQ平均有0.9分提高， fwsegSNR平均有3 dB提升。这表明本文所提算法对经一阶差分阵列处理后的残留噪声起到了进一步的抑制。本文的两种算法与Coherence算法相比在所有噪声下PESQ平均有0.25分提高， fwsegSNR平均有1.5 dB提升，去噪效果及语音质量均优于Coherence算法。

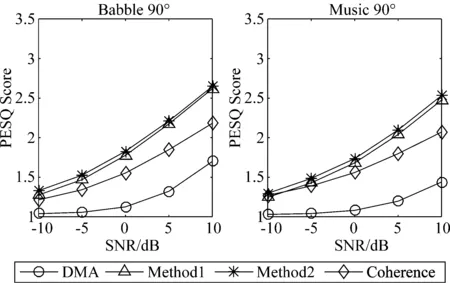
图4 不同噪声下不同算法平均PESQ得分Fig.4 Average PESQ scores of different algorithms with different noise

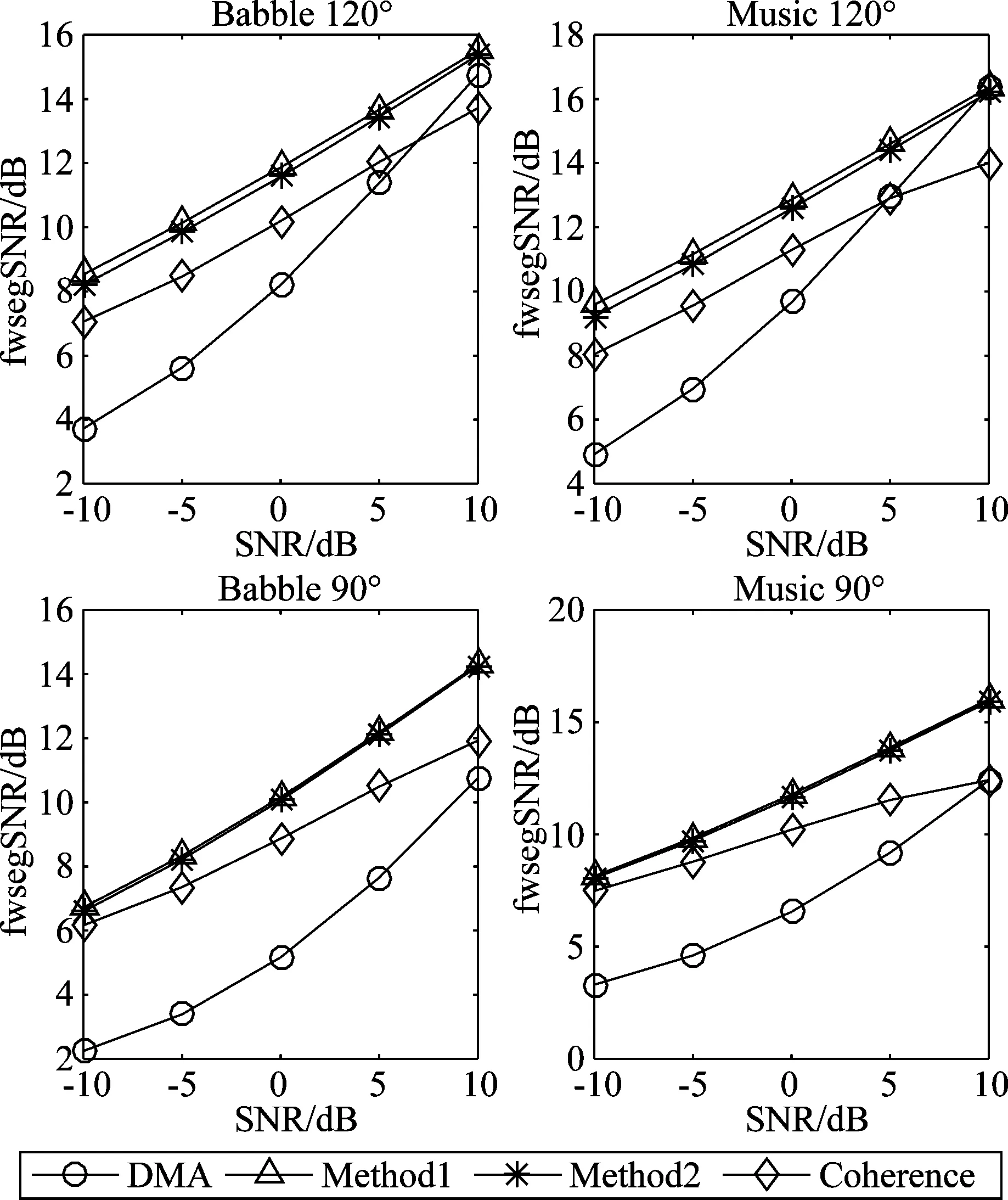
图5 不同噪声下不同算法平均fwsegSNR值Fig.5 Average fwsegSNR values of different algorithms with different noise

5 结论

本文提出了一种结合差分阵列与幅度谱减的双麦语音增强算法，该算法首先在STFT域设计了一阶差分阵列，形成了两个零点分别在180°和0°的背对背心形波束，对两麦克风采集到的带噪语音信号进行处理，得到语音通道信号和噪声通道信号。接着对语音通道信号中的残留噪声进行了分析，利用差分阵列处理后的两通道信号对语音通道信号的信噪比进行估计，然后利用幅度谱减法对残留噪声进行消除。针对语音通道信号的信噪比估计，本文给出了两种计算方法。最后对本文所提算法在不同噪声场景下从噪声抑制和语音质量两方面进行了评测，客观评测参数显示该算法有效的抑制了方向噪声，改善了语音的质量，与其他算法相比频率加权分段信噪比和语音主观质量评估打分都有一定提升。总的来说本文所提算法能够对方向性噪声起到不错的抑制作用，且计算复杂度低易于实时实现，可以用于诸如助听器之类的小型设备。