存在检测开销与检测误差的抗跟踪干扰最优跳速设计
朱勇刚 于 龙 朱义勇 贾录良
(1. 国防科技大学第六十三研究所, 江苏南京 210007; 2. 国防科技大学信息通信学院, 湖北武汉 430010;3. 陆军工程大学通信工程学院, 江苏南京 210007)
1 引言
跟踪干扰是指干扰信号能跟踪信号频率跳变的一种干扰方式,按典型实现途径,跟踪干扰可分为波形跟踪干扰、转发跟踪干扰和引导跟踪干扰三种[1]。波形跟踪干扰指干扰机在破译用户跳频图案的基础上,同步施放与跳频通信每一跳信号的时间和频率都一致的干扰信号,干扰效率高。但由于在战场复杂电磁环境下,进行实时网台分选并破译跳频图案的难度大,目前还未见实用化波形跟踪机的报导。转发跟踪干扰是将接收到的跳频通信信号直接或处理后转发出去,从而对当前跳的跳频通信频率形成干扰。转发跟踪干扰需要接收和转发整个跳频带宽内的信号,若跳频带宽足够宽,干扰机功放的大部分功率会被无效消耗,实际干扰效果不佳。引导跟踪干扰指干扰机对跳频通信信号快速检测和识别,并立即引导干扰机在该频率上施加干扰。由于该干扰方式的实现途径简单且干扰效果较好,从而被广泛使用。本文主要研究抗引导跟踪干扰方法。面对跟踪干扰,一种直接的方式是通过提高跳频速率来实现抗干扰[1]。然而,由于射频器件及自动增益控制器等的限制,用户切换频率后存在器件状态不稳定的换频时间,换频时间内用户无法进行通信[2]。在时间一定的条件下,若跳速过快,则由于换频时间的存在导致实际通信时间减少;若跳速较慢,则被敌方有效感知并实施跟踪干扰的概率增加。因此,跳频通信的最优跳速选择是一个需要解决的重要问题。
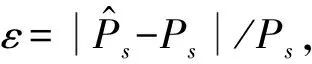
本文针对引导跟踪干扰,将跳频通信信号检测与抗干扰博弈结合起来,采用Stackelberg博弈模型[13]研究通信干扰方与抗干扰方在时域的博弈问题。在该模型中,存在一个先行者(leader)和一个跟随者(follower),通信方作为先行者首先以一定跳速进行通信,干扰方作为跟随者在已知跳速的基础上分配合适的信号检测时间和干扰时间;然后,通信方在检测到干扰方的检测时间与干扰时间后,重新调整跳频速率,博弈过程依次持续进行。本文首先建立了基于Stackelberg博弈的通信干扰与抗干扰模型,然后推导了相应的Stackelberg均衡解,并将所提方法的抗干扰性能与盲跳频和变速跳频[12]的抗跟踪干扰性能进行比较,证明了所提方法的抗跟踪干扰性能显著优于已有方法。
2 系统模型与问题描述
2.1 系统模型
典型的跳频信号结构示意图如图1所示。令跳频用户的跳频频率集为F,满足|F|=M,即跳频信号在M个相邻但不相交的子频带内伪随机跳变。假设跳频周期为T,且T∈[0,Tmax],Tmax为最大跳频周期,即跳频用户能够根据引导式跟踪干扰的参数,在0到Tmax的范围内自适应调整跳频周期。受器件和工艺水平等的限制,跳频信号的频率切换不可避免地存在不稳定的暂态过程,在该过程期间跳频通信系统既不发射也不接收信号[2]。令该暂态过程的持续时间为Tc,在跳频通信系统工作期间可以将其看成是固定值。
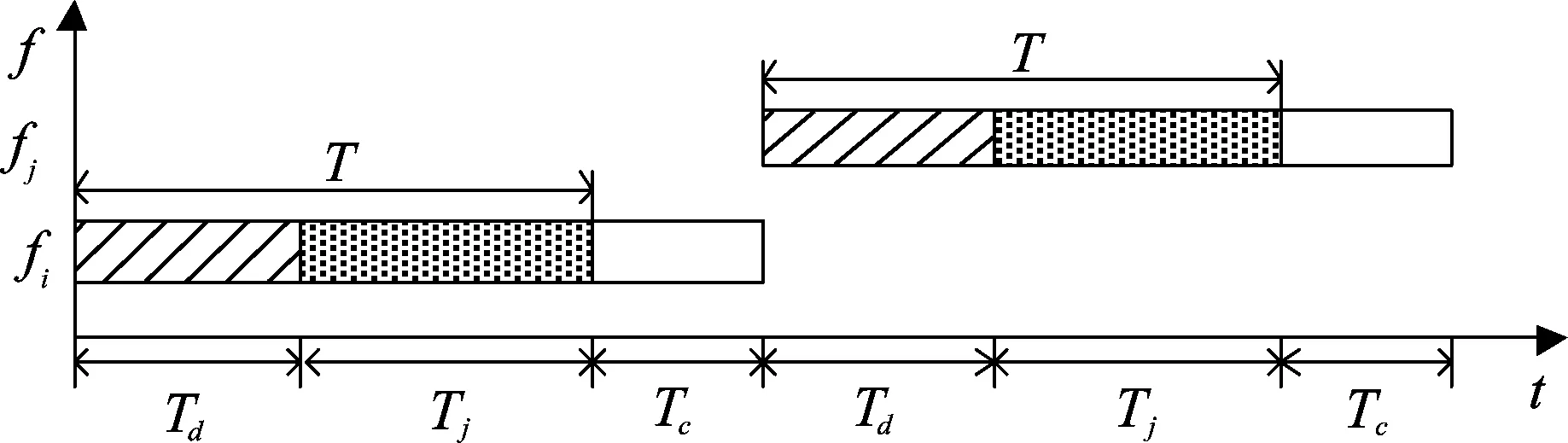
图1 跳频信号结构示意图Fig.1 The framework of frequency-hopping signal
引导式跟踪干扰的干扰策略是[10]:在每个跳频周期内,干扰方首先检测跳频信号,若检测到跳频通信信号,则立即引导干扰机进行干扰;否则,干扰机不发射干扰信号。因此,可以将每个跳周期T分成两部分:信号检测时间Td和干扰时间Tj,且T=Td+Tj。由于信号检测概率往往与检测时间或检测信号长度有关:检测时间越长,检测概率越高;反之,则越低,因此,为跳频通信信号的检测概率可以表示为p(Td),那么,一个跳周期内通信方的平均接收信噪比可以表示为:
(1)

(2)
2.2 问题描述
在通信抗干扰博弈过程中,通信方首先以一定的跳周期T进行通信,然后干扰方将根据通信方的跳周期T以合适的信号检测时间Td和干扰时间Tj进行信号检测和施放干扰,其目标是使得通信方的平均接收信噪比最小;之后,通信方将根据干扰方的信号检测时间Td和干扰时间Tj调整跳频周期T,以使得己方的平均接收信噪比最大。因此,通信方和干扰方的效用函数UC(T)和UJ(Td,Tj)可以分别表示为:
(3)
在博弈过程中,干扰方作为跟随者根据跳频通信信号的检测结果,由如下优化问题确定最优检测时间:
(4)
(5)

3 基于Stackelberg博弈的最优跳速设计
将式(2)带入式(4)、(5),并通过简要分析可知通信博弈双方的目标函数可以分别等效为:
(6)
(7)
可以看出,博弈双方的最优策略与信号检测性能p(Td)有关,下面结合具体的信号检测方法进行分析。常用的信号检测方法包括能量检测、匹配滤波检测和循环平稳特征检测等[14]。本文不以信号检测研究为重点,因此假设干扰方采用能量检测作为跳频通信信号的检测方法:对M个正交子频带的接收信号进行能量检测,取能量最大者作为跳频通信信号所在频率的估计结果。附录1给出了该检测方法的近似检测概率表达式:
(8)
其中,为便于分析,在上式中令Ts=1,即Td为归一化检测时间或采样信号个数,另外,上式中的近似处理是取m/(m+1)≈1得到的。下面,结合式(8)给出的检测概率p(Td),求解式(6)、(7)的目标函数,确定通信博弈双方的最优策略。
3.1 干扰方的最优干扰策略


(9)

(10)
干扰方的最优解由下式给出:
(11)
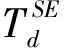
(12)

(13)
由此,得到干扰方最优干扰策略的近似解析解:
(14)
本文将在第4部分对近似解式(14)和精确解式(11)的近似程度进行比较和分析。
3.2 抗干扰方的最优抗干扰策略
为了求解通信方的最优抗干扰策略,将式(11)代入式(7),并求解可得:

(15)


附录3给出了定理1的详细证明。由式(11)以及定理1可知:干扰方和通信方的目标函数都为单峰函数,因此,存在唯一的Stackelberg均衡解。但是,通信方的目标函数都较为复杂,难以得到其导数的解析表达式,因此,采用黄金分割法寻找双方的最优解[15]。
第1步:将最大跳周期设为搜索区间,即设a1=0,b1=Tmax,k=1,搜索精度为t0>0,计算试探点λ1、μ1及对应的函数值UC(λ1)、UC(μ1),其中:λ1=a1+0.382(b1-a1),μ1=a1+0.618(b1-a1);UC(λ1)、UC(μ1)的计算可以首先将λ1、μ1分别代入式(14)计算Td(λ1)、Td(μ1)的近似解,也可以将λ1、μ1代入式(11)采用黄金分割法的方法求解Td(λ1)、Td(μ1)的精确解。
第2步:若bk-ak
第3步:ak+1=λk,bk+1=bk,λk+1=μk,μk+1=ak+1+0.618(bk+1-ak+1),计算UC(μk+1),转入第5步;
第4步:ak+1=ak,bk+1=μk,μk+1=λk,λk+1=ak+1+0.382(bk+1-ak+1),计算UC(λk+1),转入第5步;
第5步:k=k+1,转入第2步。
4 仿真与分析


图2 干扰方的目标函数曲线Fig.2 The objective curve of jammer

图3 通信方的目标函数曲线Fig.3 The objective curve of communicator
图4给出了最优检测时间的精确解和近似解(式(14))随信噪比的变化曲线。仿真中,取M=8。可以看出,随着信噪比、跳周期的变化,近似解与精确解具有相同的变化趋势,且当信噪比适中时,近似解对精确解的近似程度最好。另外,随着信噪比的增加,干扰方的最优检测时间减小。这是因为当信噪比较高时,只需较少的检测时间即可以较高的概率有效检测跳频信号,干扰方可以减小检测时间,增加干扰时间,从而获得最优干扰效果。
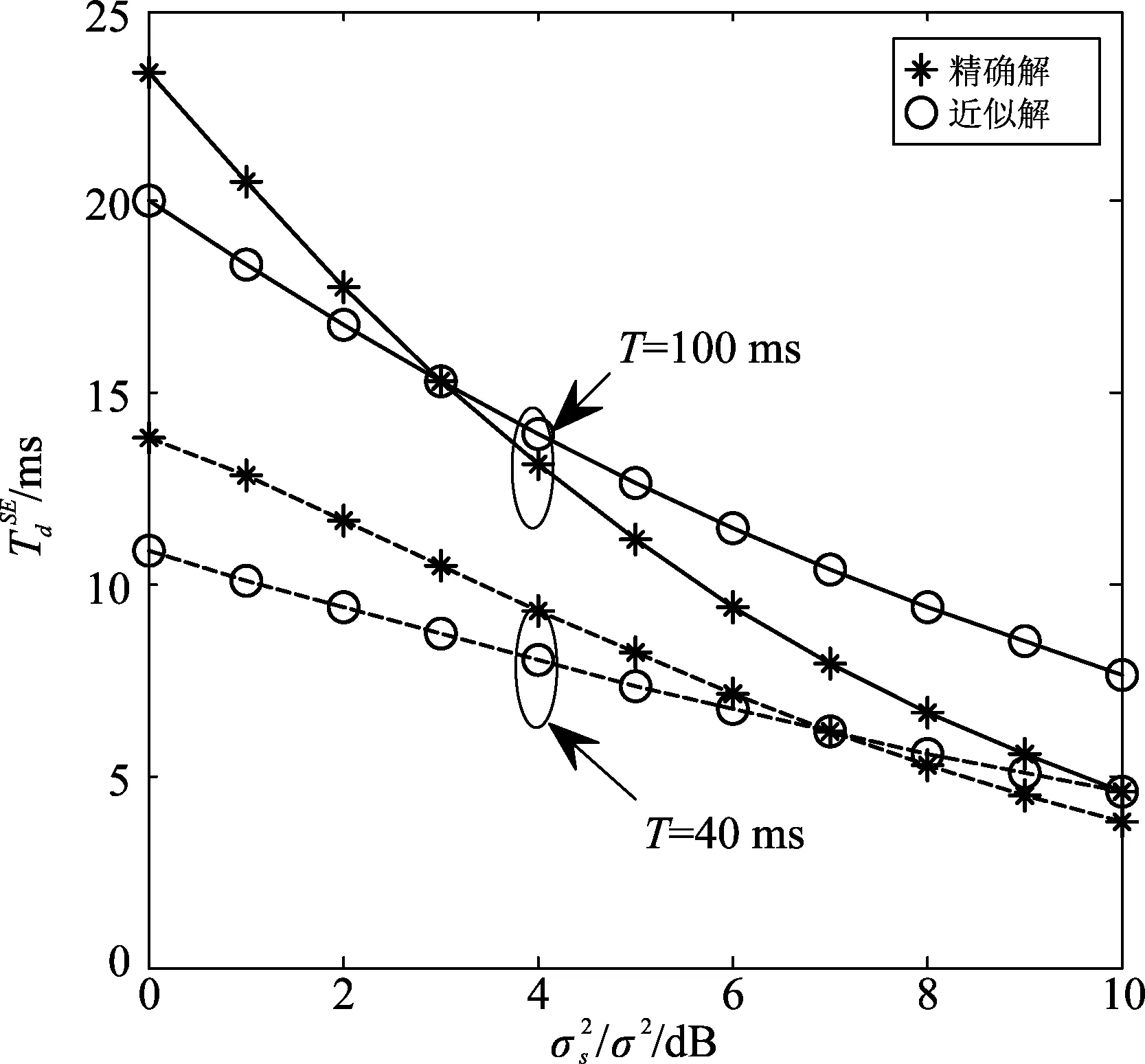
图4 最优检测时间随信噪比的变化曲线Fig.4 The optimal detection time vs. SNR
图5给出了取Tmax=50 ms时,最优跳周期随信噪比的变化曲线。可以看出,当信噪比较小时,通信方的最优跳周期较大,即采用慢跳频;当信噪比增加时,通信方的最优跳周期减小,即提高跳速。这是因为当信噪比较低时,干扰方需要较多时间用于检测跳频信号,因此通信方采用尽可能慢的跳频速率,以减小跳频损伤的影响;当信噪比较高时,干扰方能够快速检测到跳频信号,因此通信方需要提高跳速,尽可能减小干扰的影响。同时,从图5可以看出,随着信道数的增加,通信方的最优跳频周期将有所增加。

图5 最优跳周期随信噪比的变化曲线Fig.5 The optimal frequency-hopping cycle vs. SNR


图6 多种跳频模式的抗跟踪干扰性能Fig.6 The anti-following jamming performance for different hopping model
5 结论
基于博弈论的通信干扰与抗干扰是目前的研究热点之一,本文将已有的功率域、频率域的博弈框架扩展到时间域,结合干扰方检测通信信号需要付出时间开销和存在检测误差的特点,提出了存在检测误差条件下的最优跳速设计问题,并采用Stackelberg博弈模型对该问题进行了求解。理论分析与仿真结果表明,当信噪比小于4/TlnM时,干扰方的最优干扰策略是盲干扰,通信方的最优抗干扰策略是慢速跳频;反之,干扰方的最优干扰策略是先检测后干扰,通信方将相应地调整跳频周期已获得最优抗干扰性能。需要指出,尽管本文所提方法在一定程度上克服了已有研究难以考虑检测开销与检测性能的关系对最优跳速设计的不足,但该方法需要通信对抗双方准确获取对方的决策信息。下一步将结合强化学习技术研究干扰方决策信息的在线学习方法[17]。另外,本文所提方法可以与功率域、频率域博弈相结合,构造多域博弈抗干扰,以进一步提高抗干扰性能。
附录1 跳频通信信号检测概率
采用能量检测方法对M个子频带上的接收信号进行检测时,跳频通信信号的检测概率可以表示为:
p(Td)=p(R2(Td) (A1) (A2) (A3) 其中,Ts为采样周期。 对式(8)求导可知: (A4) 将Td=0代入上式并化简可得: (A5) (A6) 将式(A6)和p(0)=1/M代入式(9)得: (A7) 证明:证明的主要思路是分别针对T→0和T→的情况,分析的单调性。首先,当M较大时,式(13)给出的可以近似为进一步地,当T→0时,对根号函数进行一阶泰勒展开:(1+x)1/ 2≈1+x/ 2,因此,可以近似为下式: (A8) 同样地,对式(8)中的指数函数进行一阶泰勒展开,并将式(A8)代入其中,可得: (A9) 将式(A8)、(A9)代入式(7),得到T→0条件下通信方等效目标函数的近似表达式: (A10) 其次,当T→时,由式(13)可知其中α是与T无关的大于0的常数,同时,当T→时,p(Td)趋近于1,因此,令p(Td)=1-β,其中,β→0,将以上近似结果代入式(7),得到T→条件下通信方等效目标函数的近似表达式: (A11)
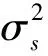

附录2 信噪比门限的求解

附录3 定理1的证明

