Kalman滤波下的多信号单通道盲源分离

何继爱 宋宇霄

(兰州理工大学计算机与通信学院，甘肃兰州 730050)

1 引言

随着物联网技术的快速发展，物联网在各个行业中都发挥着及其重要的作用[1]。窄带物联网(NB-IoT)技术因功耗低，覆盖广等优点越来越受到人们的关注。在窄带物联网通信中，由于物联网环境下传输的载体通常为单通道窄带信号[2]，在传输信号的过程中由于多设备的原因，接收机接收到的往往是多路混合的复杂信号[3- 4]。为了从复杂信号中得到有用的信号源，需要对其进行分离提取。Kalman滤波算法是一种对动态系统进行数据状态估计的有效办法[5]，它具有储存历史数据量少的优点，利用新的观测值，通过对其不断预测和修正估计出系统新的状态。随着计算机技术的不断提升，Kalman滤波在实时性、有效性、可靠性有着高要求的系统中得到了广泛的应用。

针对单通道盲源分离问题，许多学者进行探索并取得了一定的成果。文献[6]提出了在窄带物联网中基于双门限接收的单通道窄带信号盲分离算法，构造并设计了单通道窄带相关处理器，提高了盲源分离效率，但是对于多信号混合成的观测信号存在着计算量大的问题。文献[7]为了达到增强语音信号的目的，使用Kalman滤波算法对于含噪声的混合语音信号进行滤波，之后利用Fast-ICA算法对阵列语音信号进行分离，但是没有利用信号的状态空间特征对混合信号进行分离，运算复杂度较高。文献[8]提出了一种通过计算信号循环频率，构造循环谱域滤波器实现信号分离的方法，文献[9]在此基础上对循环频率误差进行修改，分析了在误差条件下滤波器的性能，但是需要根据循环谱域谱相关性得到循环频率，以确定滤波器频移量，计算复杂度高。

基于以上的研究，为了解决单传感器接收混合信号分离的准确性，提高运算效率，本文提出了一种基于Kalman滤波算法对混合信号进行状态空间估计，并分离出源信号的算法。文章第2节主要介绍了窄带物联网SCH低阶与高阶调制后接收机模型，并简单介绍了Kalman滤波算法基本模型，第3节介绍了基于Kalman滤波的多信号单通道盲源分离算法，第4节为仿真实验并对算法进行验证，第5节对文章进行总结。

2 信号及系统模型

2.1 信号模型

在窄带物联网物理层的设计中，有SCH低阶调制与SCH高阶调制，其中SCH低阶调制为BPSK信号与QPSK信号：

(1)

其中，ai=±1,k∈{1,2,3,4},g(t)为基带码元波形，n(t)为加性高斯噪声。对于SCH高阶调制，存在两个不同载波的QPSK信号共同作用，可用下式描述：

(2)

2.2 Kalman滤波算法

Kalman滤波器是基于状态空间模型的最优滤波器，在离散时间动态系统模型下，Kalman滤波由过程方程和观测方程描述，过程方程为：

a(k+1)=F(k+1,k)a(k)+v1(k)

(3)

其中，a(k)是M×1维表示系统在离散时间n的状态向量；F(k+1,k)为系统状态转移矩阵；v1(k)是M×1维的过程噪声向量。系统的观测方程：

y(k)=C(k)a(k)+v2(k)

(4)

其中，y(k)为N×1维，表示动态系统在时间k的观测向量；C(k)为N×M维观测矩阵；v2(k)是M×1维的观测噪声向量。Kailath提出N×1维新息过程，定义为：

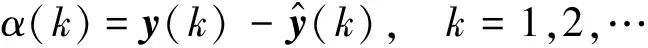
(5)

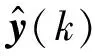
对于新息过程，定义状态向量的一步预测误差为：

(6)

R(k)=E{α(k)αH(k)}

(7)

增益矩阵在Kalman滤波中起到了至关重要的作用，在状态向量的每一次迭代更新中，都会得到增益矩阵，由增益矩阵得到当前状态的优化结果，定义增益矩阵为G(k)，则有：

G(k)=E{a(k+1)αH(k)}R-1(k)

(8)

联立式(7)与式(8)，可以得到状态向量一步预测更新公式：

(9)

由式(9)知，在k+1时刻的状态向量是由第k时刻状态向量的估计得到。在一个滤波周期内，从Kalman滤波使用的系统信息和观测信息的过程来看，Kalman滤波可以分为时间更新和状态更新两个过程，具体过程如图1所示。

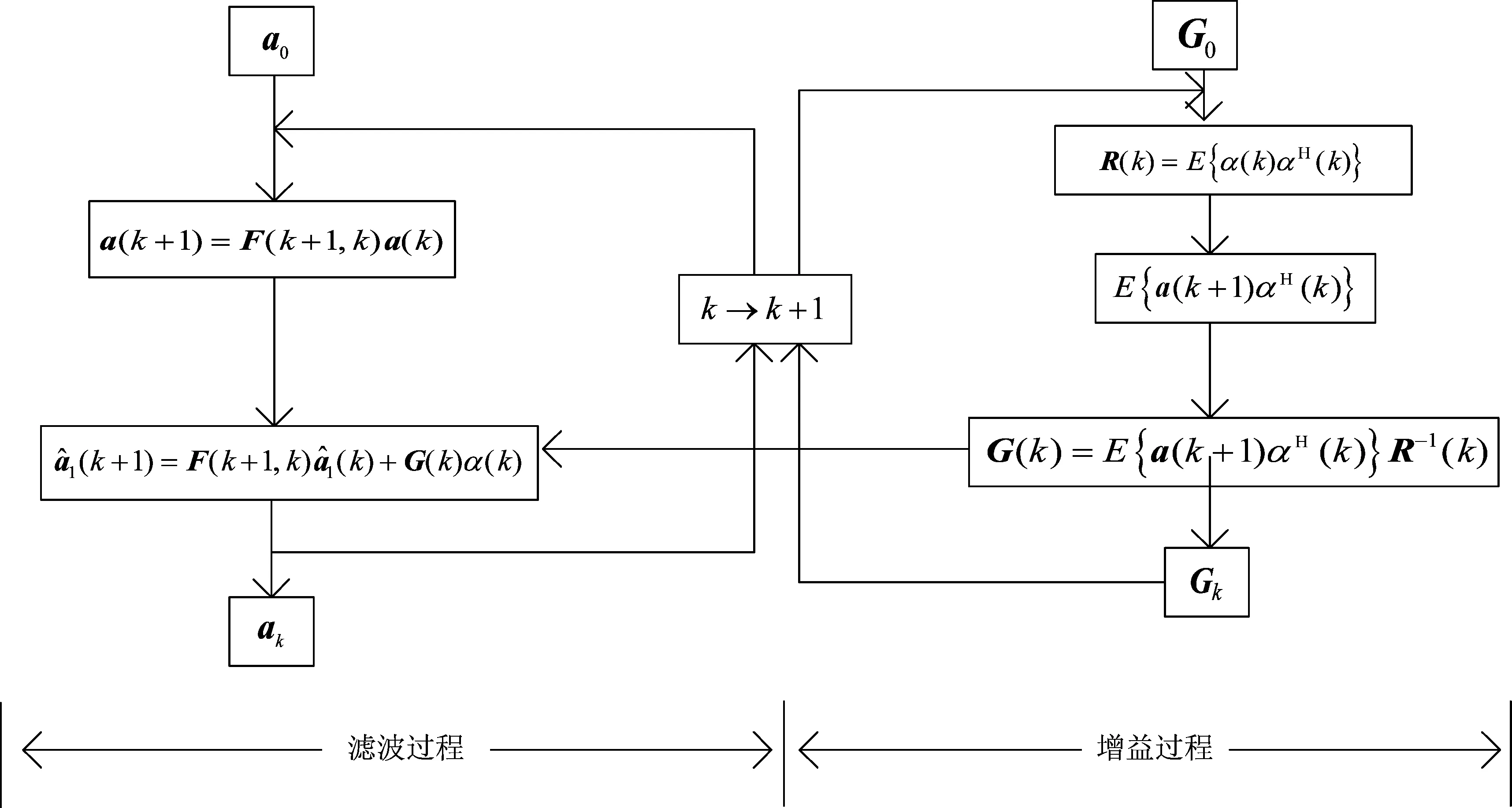
图1 Kalman算法原理Fig.1 Kalman algorithm principle

3 基于Kalman滤波的多信号单通道盲源分离算法

假设单通道混合信号C(k)是由源信号r(k)瞬时线性混合而来，为：C(k)=r1(k)+r2(k)+…+rn(k)，且信号满足以下假设条件：

(1)源信号为空间上相互独立，且各源信号具有不同的时间结构，也就是说源信号之间统计独立；

(2)观测噪声与过程噪声均为加性高斯白噪声。

为了将源信号从混合信号中分离，利用Kalman滤波算法，设其过程方程为：

a(k+1)=F(k+1,k)a(k)+v1(k)

(10)

其中，a(k)为已知源信号序列中的第一个值，a(k+1)是对信号下个状态的估计，由于在盲分离中，信号幅度具有不确定性，可将幅度对系统的影响弱化，所以F(k+1,k)为M×M的单位矩阵[11]，v1(k)为过程高斯白噪声向量。对于其观测方程为：

y(k)=C(k)a(k)+v2(k)

(11)

其中，C(k)为瞬时线性混合信号，v2(k)为观测高斯白噪声向量。由于各个源信号与噪声之间统计独立，可排除噪声对系统的影响，所以，式(10)过程方程、(11)观测方程可变换为：

a(k+1)=F(k+1,k)a(k)

y(k)=C(k)a(k)

(12)

对于式(12)观测方程中的观测矩阵C(k)，对其求协方差，得到：

(13)

在q中，用观测矩阵中的每一个值与观测平均值相减可得到观测矩阵的协方差。定义初始迭代值为δ，δ为初始值接近于零，并在零值处扰动，即Sν=δ，将Sν看作最优化的方差值，即为原始最优化的结果，在滤波过程中每次都会对此值进行更新。

在Kalman滤波算法中，我们需要对观测值中的每一个元素进行迭代并更新，得到最优估计值，即为对信源信号的最优估计：

a(k)=F×a(k-1)+q(k-1)

(14)

其中，a(k)为上一状态a(k-1)对当前结果预测的状态值，利用状态转移矩阵和上一个状态乘积加上一个状态的观测协方差，可以得到当前状态的估计值。对于Kalman滤波而言，增益矩阵G(k)有着相当重要的地位，其对每次观测值的更新都起到了承接的作用，要得到系统增益，首先需要对当前状态的估计值进行求方差处理：

p(k)=Sv(k)+q(k)

(15)

由上式可得增益的表达式为：

(16)

由式(15)和式(16)可得最佳的优化结果为：

y(k)=a(k)+G(k)×(Me(k)-a(k))

(17)

其中Me(k)为初始测量值，y(k)为当前时刻信号通过Kalman滤波器得到最佳估计结果，最后需要对方差进行更新：

p(k)=(1-G(k))×p(k-1)

(18)

在下一时刻系统迭代过程中，将得到的最佳优化方差视为方差的初值继续进行系统迭代，直到完成对源信号的估计。由此得到基于Kalman滤波的多信号单通道盲源分离算法如下：

(1)求观测矩阵的协方差矩阵；

(2)对观测值中的每一个元素进行迭代并更新，得到最优估计值；

(3)对当前状态的估计值求其方差；

(4)得到增益矩阵；

(5)得到当前时刻最佳优化结果；更新方差，返回(1)。

4 仿真实验

4.1 盲源分离评价指标

为了将分离效果以定量的形式描述，盲源分离通常是在假定源信号与混合系统的条件下，利用相关系数、信噪比、平均意见得分等作为评价指标。本文使用相关系数来表示混合信号分离后的评价标准。试验中算法处理的数据长度是有限的，信号源r(k)和盲分离信号C(k)的相关系数用样本相关系数来估计。即：

(19)

相关系数可以消除单通道盲源分离中恢复信号和源信号的幅度差异，减小了由于幅度的差异对系统造成的影响。由式(19)可知，若恢复信号与源信号相关性高，则ρij接近于1，若相关性差，则ρij接近于0。

4.2 仿真实例

为了验证本文算法的有效性，利用MATLAB 2014a语言在Windows10，主频为2.60 GHz的计算机上进行仿真验证。

实验1 假设在窄带物联网系统中，SCH低阶调制上下行信号分别为BPSK与QPSK信号，研究以三路采样点为1600，载波频率为200 Hz，幅度为1的BPSK、4FSK、QPSK信号相混合作为混合信号，如式(20)所示。源信号为BPSK、4FSK、QPSK信号，观测信号为三路信号的线性混合，如图2、图3所示，图4为分离信号。

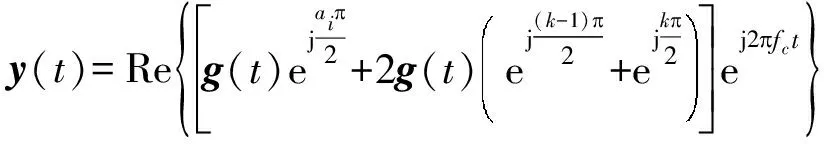
(20)

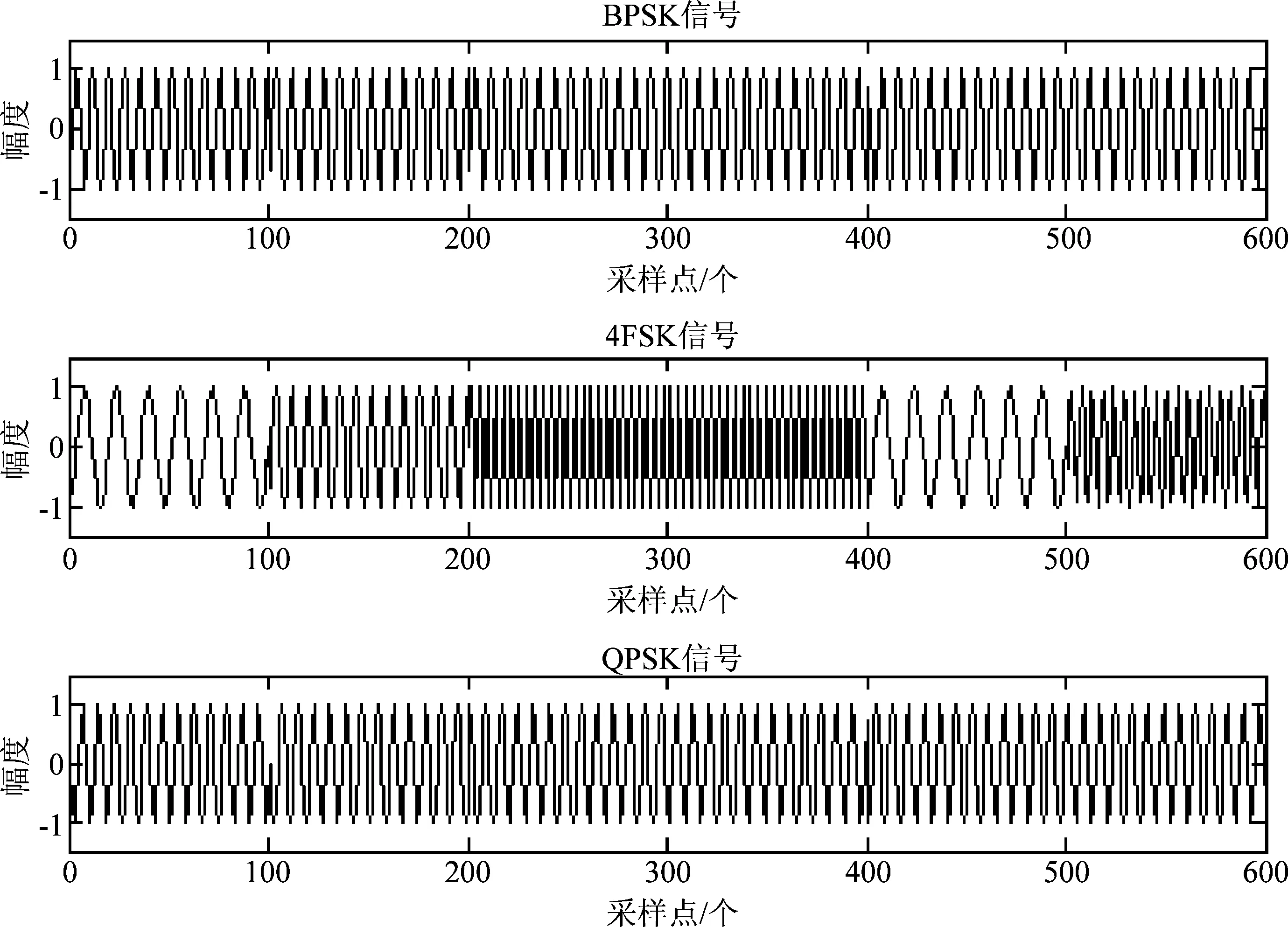
图2 实验源信号图Fig.2 Experimental source signal diagram

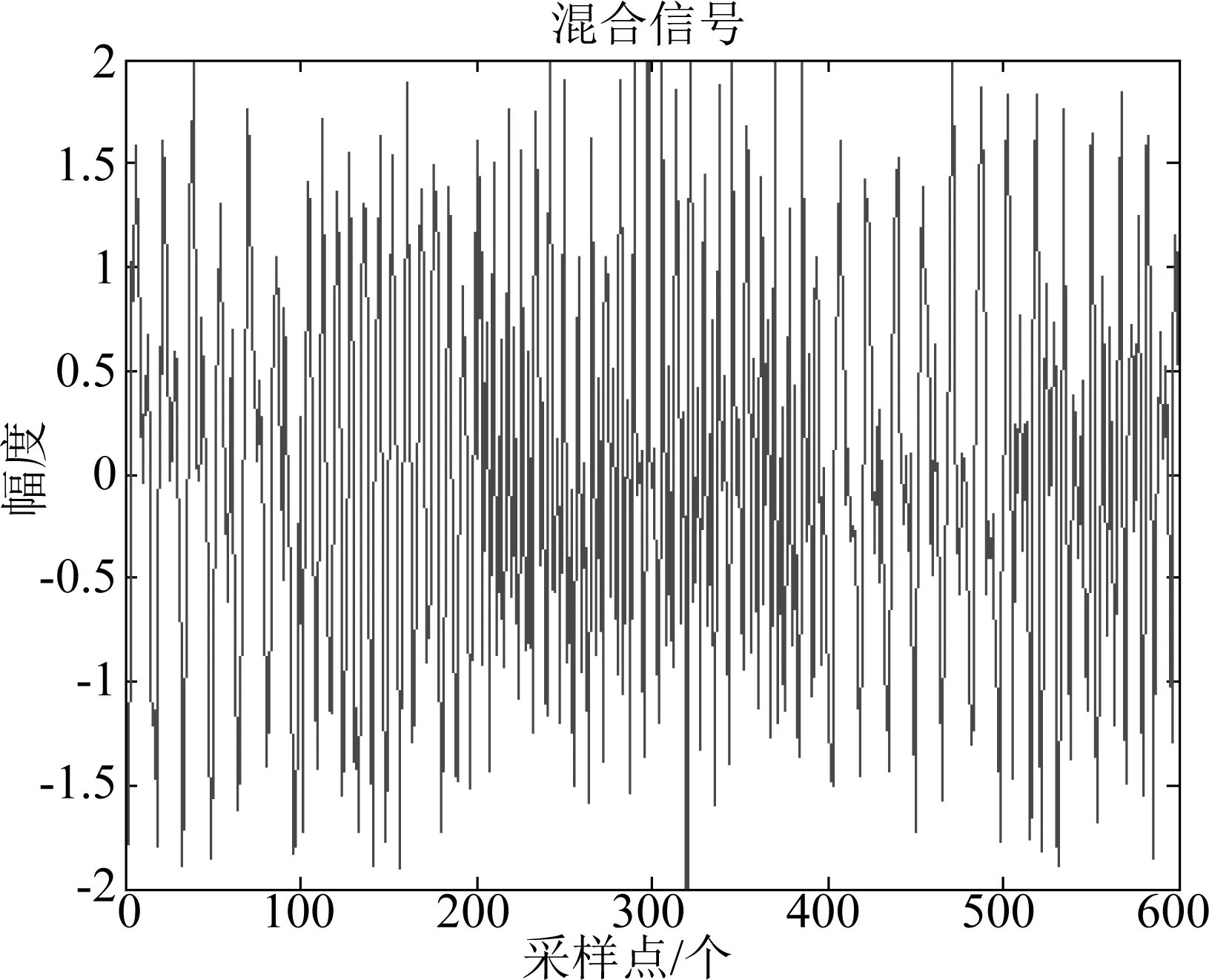
图3 实验混合信号图Fig.3 Experimental mixed signal diagram

从分离信号和源信号的图2与图4和相关系数表1可以得到，分离前后信号之间具有较高的相似程度。同样地，利用本文算法与虚拟通道法分离后的相关系数进行了对比，证明了Kalman滤波算法可以有效的将信号从混合信号中估计并有效分离。

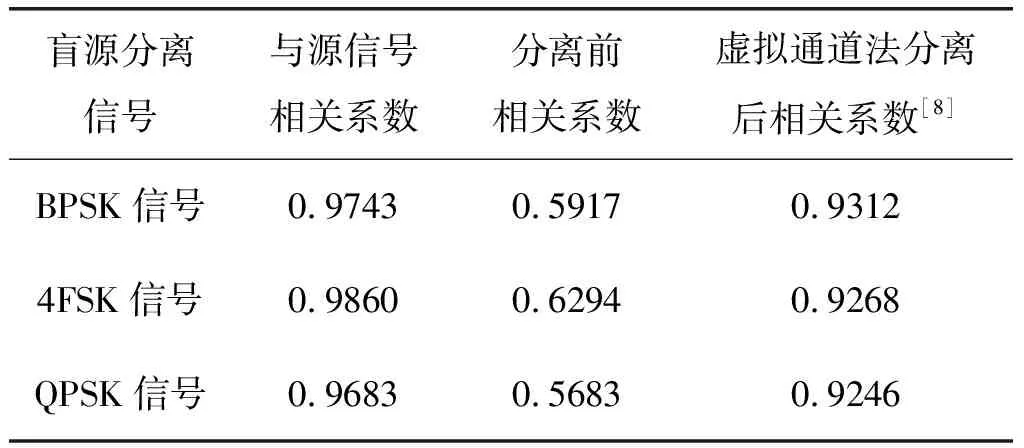
表1 分离信号与源信号相关系数

实验2 实验1表明了算法可以有效的将SCH低阶调制信号分离，提高调制效率。假设对于SCH高阶调制，分别使用载波为200 Hz与300 Hz的QPSK信号，并夹杂随机噪声序列，如式(21)所示，其中f1=200 Hz、f2=300 Hz，idin(t)为高斯随机噪声序列。图5和图6分别为源信号和混合信号，图7为分离后的信号。

(21)

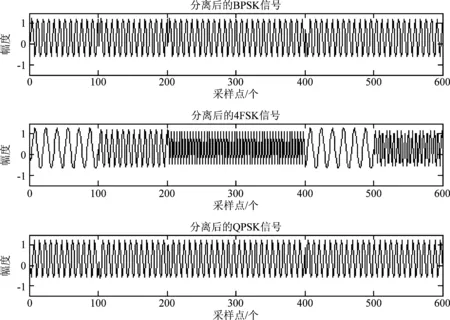
图4 实验分离信号图Fig.4 Experimental separation of signal

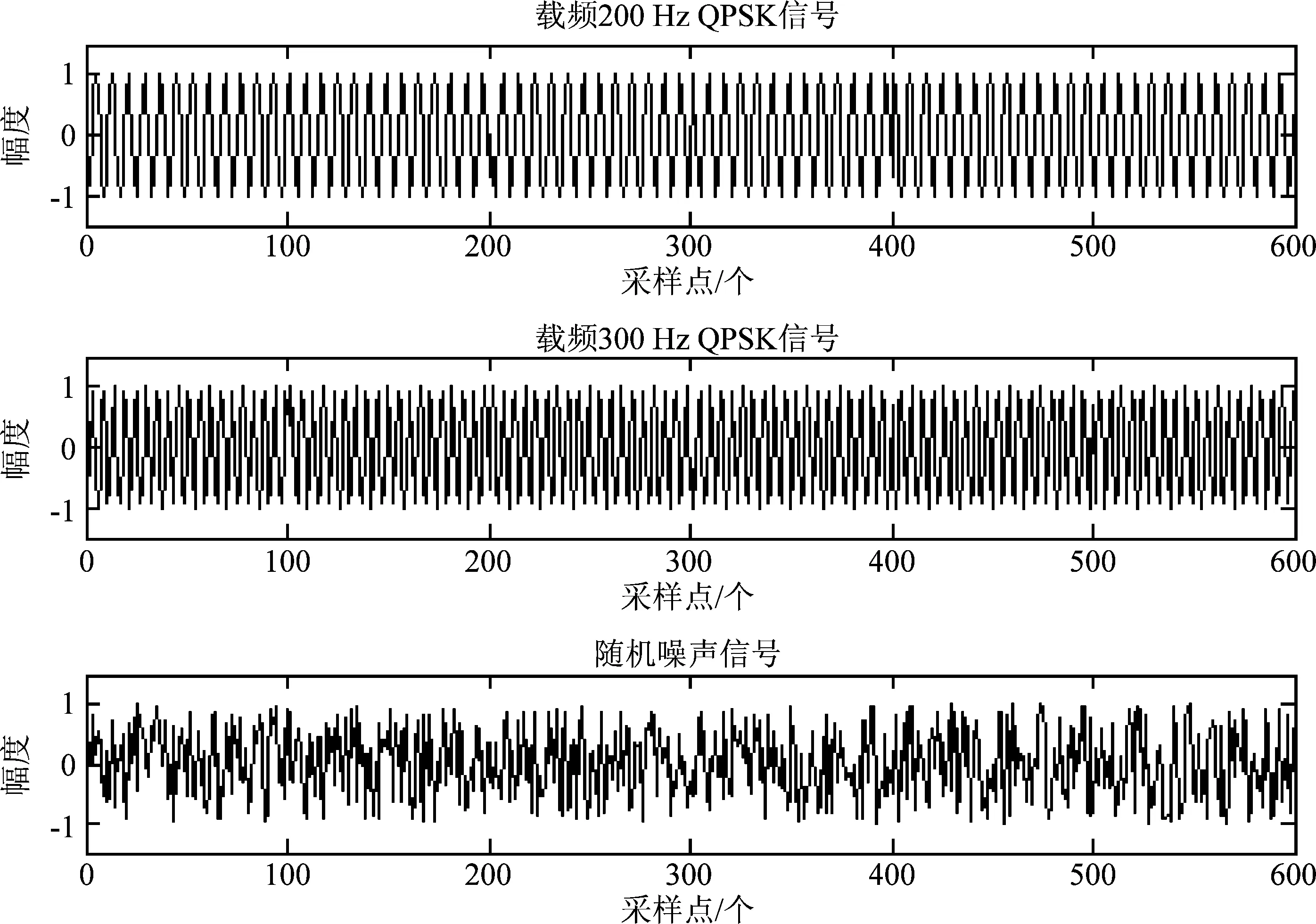
图5 实验源信号图Fig.5 Experimental source signal diagram

图6 实验混合信号图Fig.6 Experimental mixed signal diagram

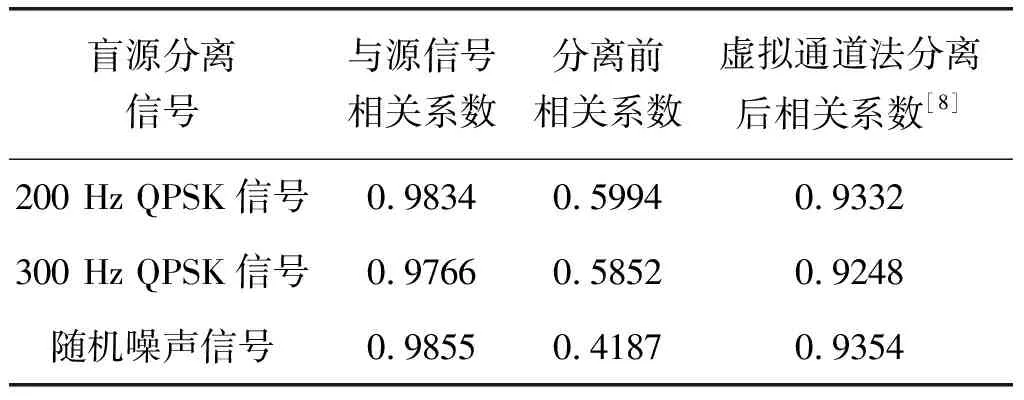
盲源分离信号与源信号相关系数分离前相关系数虚拟通道法分离后相关系数[8]200 Hz QPSK信号0.98340.59940.9332300 Hz QPSK信号0.97660.58520.9248随机噪声信号0.98550.41870.9354

从实验结果可以看出，分离信号与源信号相关系数近似为1，基于Kalman滤波算法下的单通道盲源分离算法不仅对窄带物联网物理层SCH低阶不同信号之间调制有效，而且对SCH高阶相同信号之间调制分离效果明显。

为了对比利用Kalman滤波状态估计盲源分算法得到的分离信号与Kalman算法滤除随机噪声信号后通过Fast-ICA算法得到分离信号的相关系数进行比较，结果如表3所示，通过表3可知，本文算法较文献[7]算法分离后信号具有较高的相关程度。

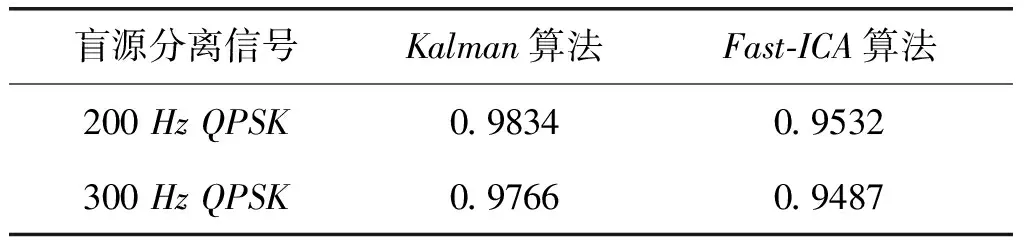
表3 Kalman滤波算法与Fast-ICA算法分离后相关系数比较

实验3 为了更好的证明Kalman滤波算法在单通道盲源分离中的有效性，假设使用了长度为1600的正弦波序列、三角波序列和随机数序列，如式(22)所示，其中sin(ft)为正弦波序列、tri(t)为三角波序列，idin(t)为高斯随机噪声信号。图8和图9分别为源信号和混合信号，图10为分离后的信号。

y(t)=sin(ft)+tri(t)+idin(t)

(22)

图7 实验分离信号图Fig.7 Experimental separation of signal

图8 实验源信号图Fig.8 Experimental source signal diagram

通过表4可知，本文使用的算法可以有效的将源信号从混合信号中分离，分离后的信号与源信号具有较高的相似度，证明了单通道盲源分离后的信号可以作为源信号的有效估计信号。

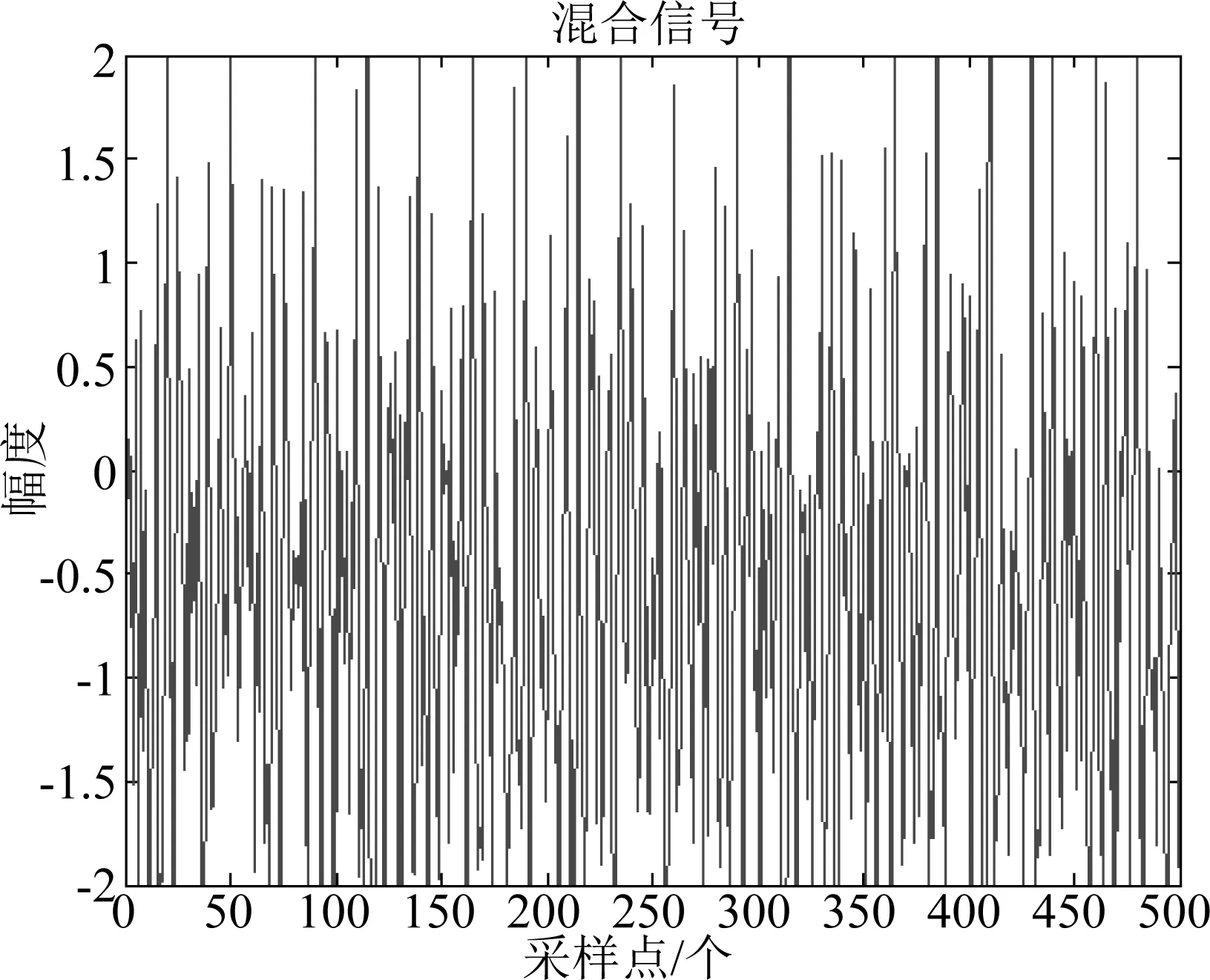
图9 实验混合信号图Fig.9 Experimental mixed signal diagram

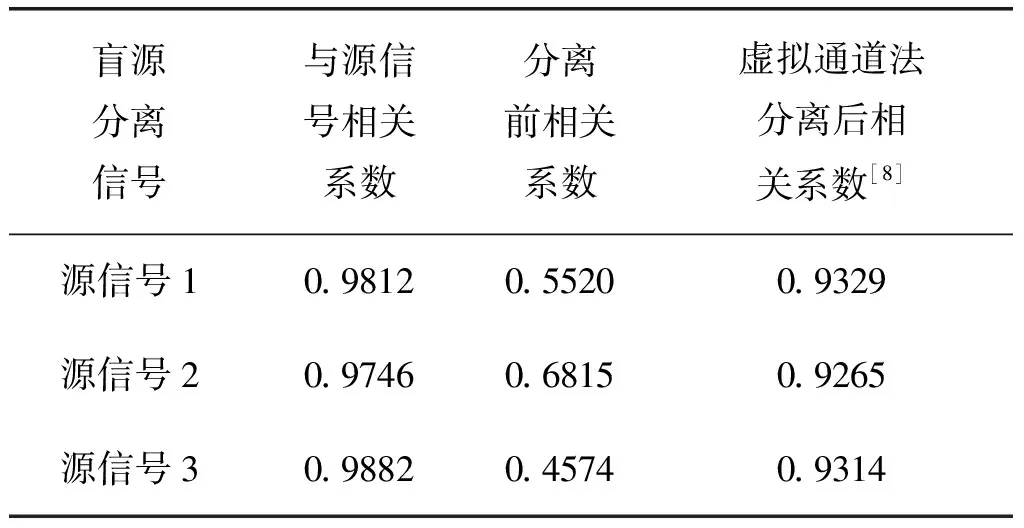
表4 分离信号与源信号相关系数

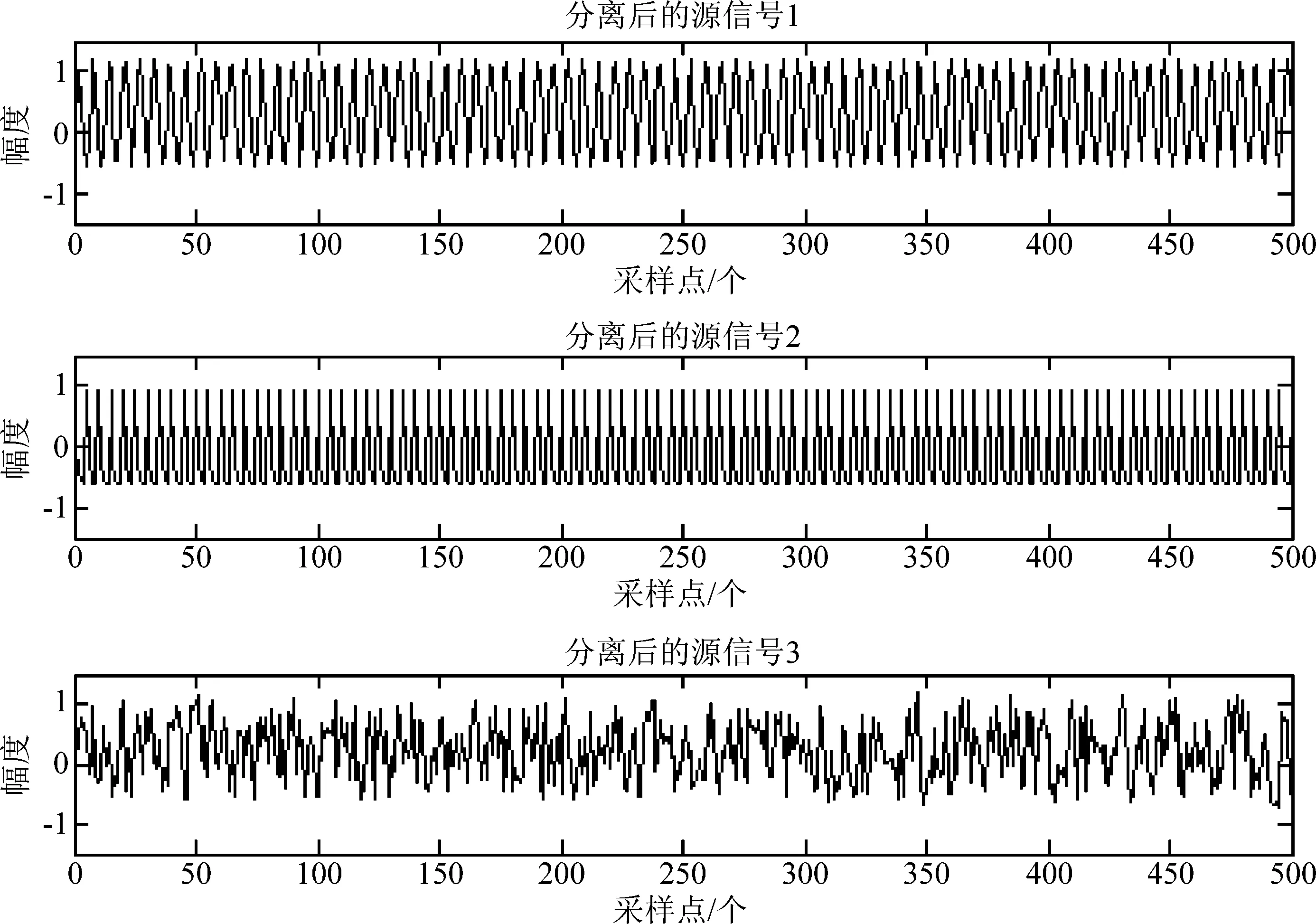
图10 实验分离信号图Fig.10 Experimental separation of signal

5 结论

本文在Kalman滤波算法的基础上，提出了基于Kalman滤波的多信号单通道盲源分离算法。该方法利用信号的时序特征与Kalman滤波算法状态空间的关系，对混合信号中的源信号进行估计，得到当前时刻最优估计状态，通过不断的时间更新和状态更新，最终得到分离信号，实现了多信号单通道盲源分离。通过仿真实验表明，本文使用的算法可以有效的从瞬时线性混合系统中恢复出源信号，具有良好的分离性能。