动态选择消息更新的SCMA多用户检测算法
谢 欢 胡艳军 蒋 芳
(安徽大学计算智能与信号处理教育部重点实验室,安徽合肥 230039)
1 引言
第五代移动通信(5G)[1]被提出以满足更高的业务要求,非正交多址技术(Non-orthogonal Multiple Access,NOMA)[2]频谱效率较高,因此成为5G的一个备选方案。作为NOMA技术的一种,从低密度信号(Low Density Signature,LDS)[3]发展来的稀疏码多址接入(Sparse Code Multiple Access,SCMA)[4]技术,可利用码字的稀疏性得到较高的接入量。因为接收的是各用户码的叠加信号,所以要进行多用户检测。由于码字是稀疏的,因此可用消息传递算法(Message Passing Algorithm,MPA)[5]进行检测。
但MPA的高计算复杂度限制了SCMA技术的实际应用。影响复杂度的因素有算法的迭代次数、码本大小、系统因子图中的分支数等。文献[6]通过简化星座图来减小码本大小。文献[7- 8]在每次迭代中将节点消息的更新顺序重新编排,越靠后更新的节点消息越有效,因此减少了迭代次数。文献[9-10]根据信道条件差异,将信道条件差的分支近似为高斯噪声,同时添加反馈机制来弥补性能的下降,通过减少分支来降低复杂度。文献[11]提出了一种基于动态因子图的MPA检测器,因子图中置信度较高的分支从当前迭代开始将不参与消息传递。文献[12]提出了一种部分边缘化的MPA(Partial Marginalization-Message Passing Algorithm,PM-MPA),迭代结束前将部分用户数据先解出来,在后续迭代中再解出剩余用户数据,牺牲了一部分性能的同时带来了复杂度下降的收益。
以上文献中算法的节点更新方法基本一致,各节点将其概率分布状态传递给相邻节点,从而改变相邻节点的概率分布状态。所有节点消息更新后,进入下一轮节点消息更新。当所有节点的码字消息概率收敛后迭代结束,接着进行软解码。因为每次迭代要更新所有码字消息,所以复杂度较高。基于实验的研究发现,一些节点比其他节点收敛快[8],意味着各码字消息的收敛速度不同。针对这一特点,为降低算法复杂度,本文提出了一种动态选择消息更新的检测算法DSM-MPA(Dynamically Select Message-Message Passing Algorithm,DSM-MPA)。不同于文献[8],本文算法在单次迭代中,不再更新因子图中的所有节点消息,只选择更新收敛较慢的节点消息,通过减少消息更新次数来降低算法复杂度。消息若收敛快,则其概率变化量小而接近收敛值,可直接用于软解码。仿真结果表明,选择合适的比重因子,相比较于原始MPA,本文算法的复杂度明显下降,同时误比特率(Bit Error Rate,BER)性能基本不变。在实际应用中可降低上行链路接收机设计复杂度,同时保证性能。
本文其余部分安排如下:第2节简述SCMA系统模型及MPA算法;第3节给出本文的改进算法;第4节对仿真结果进行性能比较分析;最后第5节给出结论。
2 系统模型
2.1 SCMA系统模型
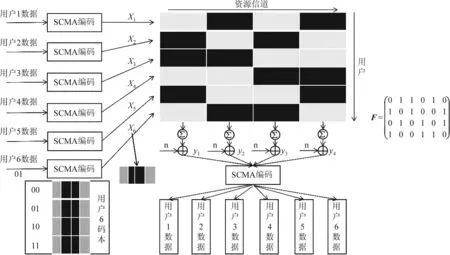
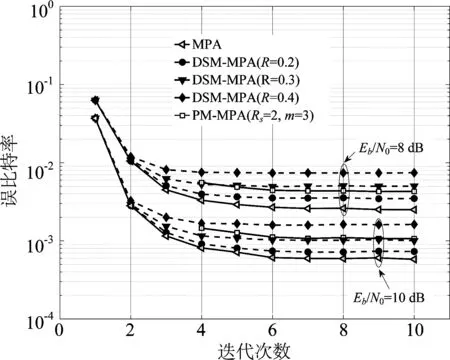
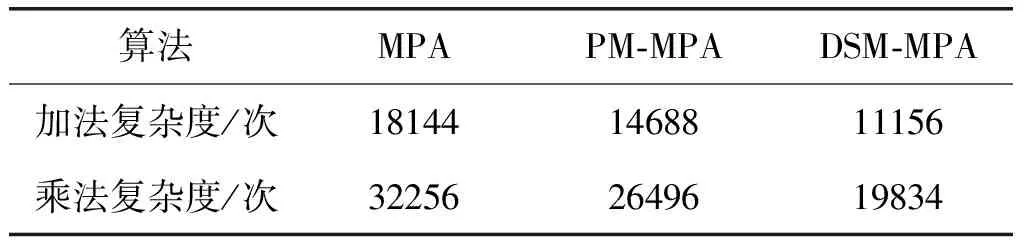
假定有J个用户共享K个资源块(J>K),则该系统的过载系数定义为λ=J/K。对于每个用户j,其比特数据与此用户码本χj中的SCMA码一一对应,χ的维度是K。码本中的SCMA码表示为xj。K维SCMA码中非零元素个数为N,N 接收信号可写为: (1) 其中,xj=[x1jx2j...xKj]T为用户j的SCMA码,hj=[h1jh2j...hKj]T为用户j的信道条件向量,n是高斯白噪声,n~CN(0,σ2I),y=[y1y2...yK]T是接收端从K个资源块中检测到的信号。 由接收信号y和信道条件H=[h1h2...hJ]T,就可通过最大后验概率估计算法(Maximum A Posteriori, MAP)来检测用户数据X=[x1x2...xJ],如式(2): (2) 图1 SCMA系统模型Fig.1 Model of SCMA system (3) (4) 其中,t表示第t次迭代,ξk是与资源块k连接的用户序号集合,ζj是用户j所占用的资源块序号集合,xjm∈[xj1xj2...xjM]T为用户j码本中第m个码字。yk为资源块k上检测的信号,σ是噪声的标准差,hk,p和xk,p分别是资源块k与用户间的信道条件向量和用户码。 图2 MPA算法示意图,实线表示来自其他边缘的先验概率,虚线表示边缘上消息的更新Fig.2 Scheme diagram of MPA. The solid line indicates the prior probability from other edges. The dashed line indicates the update of the message at the edge MPA达到最大迭代次数T后,各用户码字xjm出现的概率Q(xjm)用式(5)来计算: (5) 原始MPA迭代更新所有码字消息,直到每个码字消息收敛。所以,MPA算法复杂度较高。实际上,有些码字消息可以更快地接近收敛值,对这些消息继续更新,所得的概率值变化量小。因此,可以有选择地更新收敛较慢的消息,提前结束更新收敛快的消息。因为退出更新的消息已接近收敛,所以可直接用于软解码。在保持性能的同时,通过减少消息更新次数来降低计算复杂度。 针对以上问题,本文提出了一种动态选择消息更新的MPA。在保持BER性能与原始MPA基本相同的情况下,可明显降低算法复杂度。 算法基本思想是:第一次迭代更新所有码字消息;从第二次迭代开始,对参与此次迭代的消息,用式(6)来计算迭代前后消息的差值Dt(xjm): (6) 若差值小,则表明此消息的变化量较小,收敛速度较快。将所有Dt(xjm)值按大小排序,选出差值最小的Nit个码字消息。这Nit个码字消息将被判为收敛最快,在后续迭代中将不更新。定义R为比重因子,被判为差值最小的消息数Nit,用式(7)来计算: Nit=R·Nat (7) (8) (9) (10) 算法过程如表1。 表1 动态选择消息更新的MPA算法 续表1 本文算法与原始MPA[9]以及PM-MPA[12](m和Rs是算法中的参数)可用表2来比较复杂度,以算法执行的加法和乘法次数为衡量标准。 为了验证本文算法在上行SCMA无线通信系统中的性能,将本文算法与原始MPA以及PM-MPA进行了仿真比较实验。仿真参数如表3所示。 表2 复杂度比较 表3 仿真参数 在图3中,最上面的五条曲线是原始MPA,PM-MPA(m=3,Rs=2)以及本文算法(前两者算法曲线用实线表示,本文算法用虚线表示)在Eb/N0取8dB时的收敛情况;最下面五条曲线是各算法在Eb/N0取10dB时的收敛情况。本文算法取R=0.2和0.3时,收敛性与原始MPA和PM-MPA一致,迭代6次后收敛。本文算法R取0.4时,3次迭代后大多消息已不再更新,因此相比于原始MPA会提前收敛。但R取值比较大时,判为收敛快的消息中有很多未达到收敛条件。提前停止更新这些消息,会使后面软解码误差较大,造成BER性能大幅下降。由图3、图4可知,当信道条件较差(Eb/N0≤8dB),噪声对消息传递的干扰较大,为保证BER性能,R取值应该小(R<=0.2);当信道条件较好(Eb/N0≥8dB)时噪声小,对消息传递的干扰小,少数迭代后趋于收敛的消息多,所以R可取较大值(R>=0.2)。但为保障BER性能,R取值应小于0.3。 图3 各算法收敛速度Fig.3 Convergence rate of various algorithm 比重因子R取值若越小(R<=0.2),对于迭代中被判为收敛快的消息,其前后迭代的差值就越小。因此,这些消息的概率分布也更容易趋于稳态。这些不更新的消息越接近收敛,其他消息更新得到的收敛值与原始MPA的就更接近。因此,图4中本文算法BER性能会与原始MPA更接近。反之,R取值越大(R>=0.2),收敛快的消息中不满足收敛条件的就越多。停止更新这些消息会使其他消息难以收敛到原始MPA的值,消息可靠性就越低,BER性能将越差。 图4 各算法性能Fig.4 Performance of various algorithm 图4中各算法迭代次数都为T=6。在BER=1.0×10-3时,取R=0.2,每次迭代中被判为收敛快的消息数较少。前面提到,R取值越小(R<=0.2),这些消息的概率分布更接近稳态,可直接传递给其他消息的后续更新,对其他消息收敛到原稳定值影响小。因此,所有消息的最终概率分布接近于原始MPA。所以,此时本文算法BER性能基本和原始MPA一致;和PM-MPA算法相比,本文算法有0.5dB左右的增益。因为PM-MPA是直接提前解特定用户的数据,此用户消息可能依然与稳定值相差较远,已收敛消息的准确性不如本文算法。因此,选择合适的R,本文算法的BER性能要优于PM-MPA算法。R取0.3和0.4时,由于R取值较大,本文算法的性能损失较多,相比原始MPA分别下降了0.7dB和1.2dB。 由表2中各算法复杂度可知,比重因子R取值越大,本文算法相比于其他两种,复杂度就越低。由图3、图4可知,为有效地降低算法复杂度,同时保障BER性能,取比重因子R=0.2,迭代次数T=6。结合表2,如表4所示,原始MPA、PM-MPA(m=3,Rs=2)及本文(R=0.2)算法所执行的加法次数分别为18144次、14688次和11156次;执行的乘法次数分别为32256次、26496次和19834次。本文算法相比于原始MPA,加法次数减少了约38.5%,乘法次数减少了约38.5%。PM-MPA为保障解码性能,提前解出的用户节点数是很有限的,相比于本文算法可以降低的复杂度有限。与PM-MPA相比,本文算法的加法次数减少了约24.0%,乘法次数减少了约25.1%。综上所述,参数R取0.2比较合理。此时,BER性能基本与原始MPA一致,优于PM-MPA,同时复杂度都明显低于这两种算法。 表4 各算法复杂度比较 原始MPA每次迭代会更新所有码字消息,直到所有码字消息概率收敛后迭代结束,因此复杂度较高。为降低复杂度,针对不同码字消息概率的收敛速度不同,本文提出了一种动态选择消息更新的DSM-MPA算法。在当次迭代中找出收敛最快的码字消息,这些消息将不再更新,通过减少消息更新次数来降低复杂度。选择合适的比重因子,可使BER性能基本与原始MPA一致,并且复杂度更低;和PM-MPA相比,不仅复杂度较低,且性能也有优势。所以,本文算法在SCMA系统的应用中优势明显,可降低接收机设计复杂度,同时可以保持性能。但该算法仍存在一些不足,如比重因子R的选择固定。当信道条件变化时,每次迭代中选出的不更新的消息,就带有随机和波动性。有些消息实际并未收敛或接近收敛,这将给解码带来较大误差。因此,可设定硬性的收敛判定条件,以更有效地选择已收敛的消息不更新。可弥补由随机和波动性带来的性能损失,并可适应信道变化。2.2 原始MPA
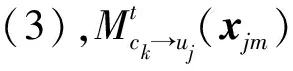

3 本文提出的算法
3.1 动态选择消息更新的MPA
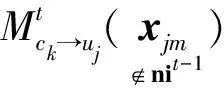



3.2 复杂度分析
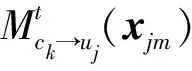
4 仿真结果与分析


4.1 性能分析

4.2 复杂度对比
5 结论

