HDI板孔群的K-means聚类及加工路径优化研究*

张明禄，李忠学，陈辅斌

(兰州交通大学 机电工程学院，兰州 730070)

0 引言

近几年移动终端的HDI板增长迅猛。由于HDI板具备更高密度的电路互通、更多的电子元器件容纳量等特性，逐渐成苹果、华为、OPPO等智能手机为代表的主流PCB板。在HDI板加工工艺方面，钻孔工序通常是PCB厂的产能瓶颈之一,钻孔的费用通常占PCB制板费用的四成。传统孔群加工主要采用机械钻孔，但它存在钻头易磨损、断裂率高、钻头昂贵、钻孔偏移量等突出问题，而激光打孔技术(Laser drilling technology)具有无需接触工件，无工具损耗，加工速度快等优点，因此适合数量多、高密度的HDI板微孔加工[1]。对于高密度、微型化的HDI孔群加工，打孔的序列孔如不仔细考虑就能导致在钻孔过程中距离和成本的额外增加，因此在最短的时间内以最优的路径完成高密度HDI微孔的加工尤为重要。

传统的精确算法(如分枝界定法等)虽然能精确求解该类问题，但随着问题规模的增大，对于这种组合爆炸式的问题会出现失效[2]。Saelal等[3]采用一种启发式蚁群算法应用于PCB孔钻削加工路径优化，能够有效地寻找加工的最佳路径。但参数α、β设置不当会导致收敛速度慢，易陷入局部最优解。Kanagaraj等[4]提出一种混合CS算法，利用其莱维飞行(Levy flight)搜索范围广、随机性高的优点，应用于孔群数量少的钻孔路径优化问题上，获得了较好的试验结果。许兆美等[5]提出在TSP优化问题的基础上，采用遗传算法能解决PCB孔群加工路径优化问题，但钻孔数量增大时，算法的优化结果和优化效率下降。徐向美等[6]采用图像分割方法，对区域内的孔群用遗传算法优化路径，但图像分割法存在噪声敏感，分割区域不连续等缺点。

本文充分考虑到HDI微孔数量多、分布密度不均，一般混合启发式算法在求解最优路径时效率较差、运行时间长、最优解不理想等问题，提出一种综合聚类算法和改进退火算法相结合的解决方案。采用K-均值算法进行聚类分析得到聚类中心及周边关联度较高微孔的分布，然后利用改进退火算法求解每一聚类区域的最优路径。

1 微孔加工模型

微孔是HDI板重要组成部分之一,通常分为导通孔与不导通孔。导通孔包括零件孔与连接不同层间的过孔，孔壁有铜箔相连;不导通孔包括固定板卡的机械孔等,孔壁无铜;过孔可分为穿透式导通孔、埋孔和盲孔；穿透式导通孔是从顶层直接通到底层；盲孔是仅延伸到印刷板的一个表面的导通孔；而埋孔是将内部两个里层之间相互连接,没有穿透底层或顶层的导通孔如图1所示[7]。

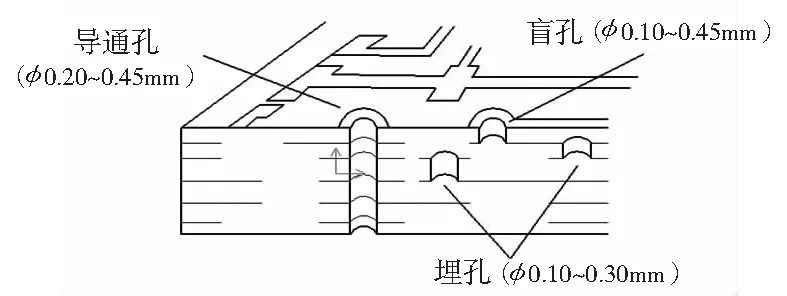
图1 微孔分布图

激光打孔机是通过电流计进行X-Y微动,将光点打到板面上所欲对准的靶位，一旦达到材料蒸发温度,立即蒸发,产生气化现象，形成微孔。当微孔完成后,即快速移往下一个微孔再继续打孔。当HDI板上有N个微孔需要加工，激光打孔路径是对所有微孔不重复地逐一进行加工所经过的距离[8]。该过程可以用图论的思想描述：设G={V(G),E(G)}为一个图，其中(G)是非空集合，V(G)中的元素为此图的顶点，V(G)={1,2...n}即为微孔的序号。对于每一条边e∈E(G),都赋予一个“权重”Dij，Dij为边e的长度，即一个微孔到下一个微孔之间的距离。图G中不重复经过V(G)中所有顶点的一条路线，代表加工微孔的一条路径，“权重”Dij之和代表加工路径之和。根据图论的知识，建立以最短路径为目标函数的数学模型[9]如公式(1)所示：

(1)

式中：权重Dij表示微孔i到微孔j之间的距离。

2 算法设计与分析

2.1 方案总体设计

整个方案的处理过程可以用图2来表示。

① K-means聚类算法对孔群进行分类,划分孔群区域；

② 每一个聚类中心区域，用改进遗传算法作路径优化。

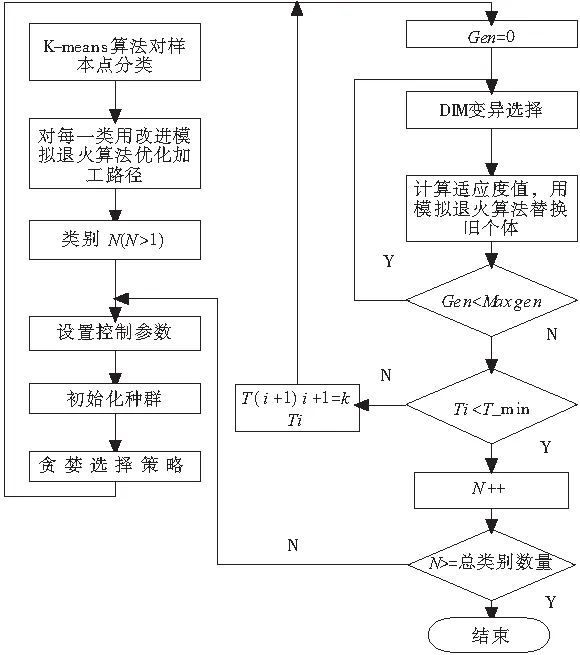
图2 总体方案

2.2 聚类算法

聚类分析是研究(样品或指标)分类问题的一种统计分析方法，同时也是数据挖掘的一个重要算法。以相似性为基础，在一个聚类中的模式之间比不在同一聚类中的模式之间具有更多的相似性[10]。

该方案采用K-means聚类算法对微型孔群进行分类。K-means算法是很典型的基于距离的聚类算法，采用距离作为相似性的评价指标，即认为两个对象的距离越近，其相似度就越大[11]。该算法认为簇是由距离靠近的对象组成的，因此把得到紧凑且独立的簇作为最终目标。其准则函数为：

(2)

其中，si表示第j个聚类集，uj为第j个聚类中心；Nj为第j个聚类集si中所包含的样本个数；xij表示分配到第j个聚类集中的第i个样本。

其计算步骤如图3所示。

图3 聚类过程

(1)从n=5个数据对象任意选择k=2个对象作为初始聚类中心；

(2)根据每个聚类对象的均值(中心对象)，计算每个对象与这些中心对象的距离;并根据最小距离重新对相应对象进行划分；

(3)重新计算每个(有变化)聚类的均值(中心对象)；

(4)循环(2)～(3)直到每个聚类不再发生变化为止。

2.3 改进模拟退火算法

模拟退火算法(SAA)由N.Metropolis等人提出，在1983年S.Kirkpatrick等人成功地将其引入组合优化领域[12]。模拟退火算法虽然具有全局最优化，但是它也存在着局限性：温度T的初值和减少步长较难确定、容易陷入局部最优解、求解时间过长等。针对传统模拟退火算法存在的问题，改进主要从前期初始种群的选择和后期种群多样性等方面入手[13]。

2.3.1 贪婪选择策略

传统模拟退火算法中初始化种群是通过randperm函数随机生成，其中有很大的概率得到较差的种群，而运用贪婪选择策略可以得到适应度较高的初始种群。其贪婪选择策略的基本思想[14]，如图4所示。

图4 贪婪选择策略流程图

2.3.2 DIM变异算子

变异是产生子代新个体的一种不可缺少的方式。变异算子是对两个随机选择的基因位之间的基因作重排，增加种群的多样性[15]。遗传算法中发展出很多变异算子，比如插入变异(IM)、移位变异(DM)、散播变异(SM)、倒置变异(IVM)、倒置移位变异(DIM)等。本文采用DIM变异算子，增加对基因选择上的随机操作性。

实施步骤：

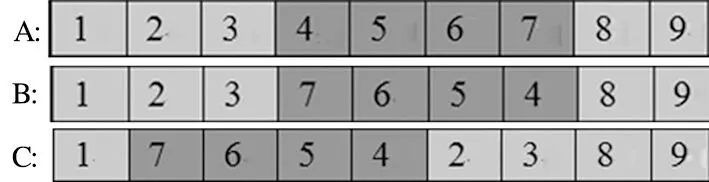
第1步：从A父代染色体中随机生成基因位4和基因位7；

第2步：将A父代中基因位4和位7之间的基因，两两对应颠倒排列，生成B子代染色体；

第3步：再将B子代中基因位7和位4之间的基因作为整体，移到原始染色体中某个随机产生的基因位前，生成C子代。

3 方案验证结果与分析

本文利用以上方案求解HDI激光打孔的路径优化问题，以HDI板上高密度的孔群作为研究实例，坐标点见图5，要求合理规划激光打孔序列，求解路径L的最小值。

首先，基于 K-means 算法对 HDI板的121个微孔进行聚类分析，求解出2个聚类中心坐标，及每个聚类中心点附近的微孔如图5和表1所示。

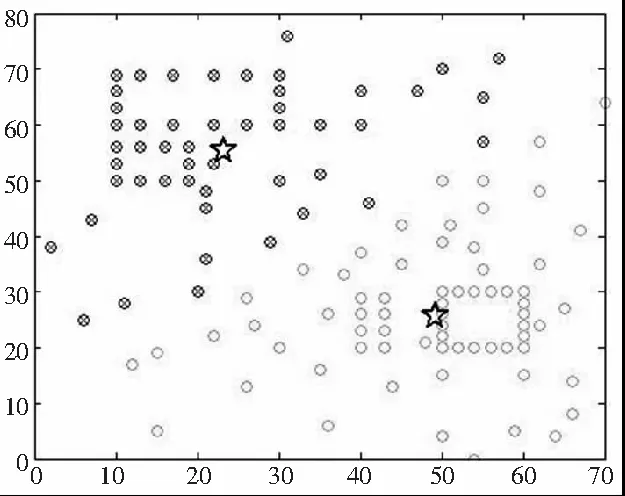
图5 聚类分析

表1 K-means 聚类结果

然后，采用改进模拟退火算法求解孔群加工路径优化，分别优化两个聚类数据的孔群加工路径。改进模拟退火算法设置tf=0.001、alpha=0.60，迭代结束后，求得最优路径见表2和图6所示，优化后路径的距离之和为633.4344mm。

表2 路径优化结果

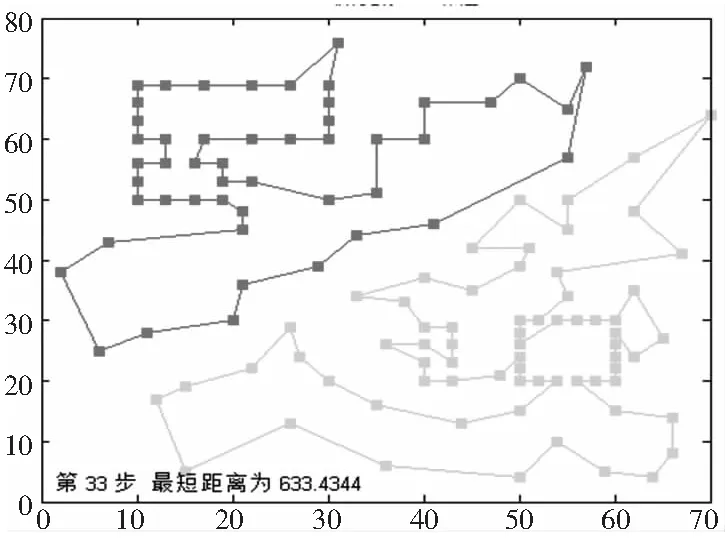
图6 路径优化

对比其他算法的优化结果见表3和图7所示，改进的模拟退火算法具有明显优势，能更好的选出初始种群，迅速降低起始的搜索范围(4000mm降到1000mm)，说明贪婪选择策略的有效性。传统模拟退火算法优化到1067.9mm时陷入局部最优解，采用DIM算子增加了种群多样性，使其跳出局部最优解，得到更优的解为766.8101mm。本文设计的方案利用K-means算法对高密度的孔群分类，再采用改进模拟退火算法优化，其效果更为明显，求得孔群加工路径最优解为633.4344mm。

表3 算法结果对比

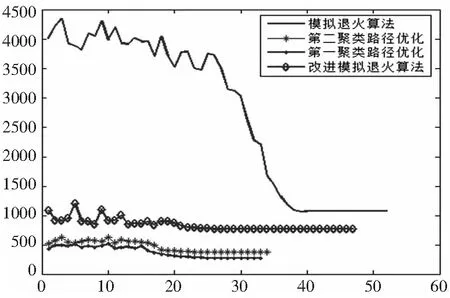
图7 算法对比图

4 结论

(1)以高密度HDI板的121个微孔作为研究实例，采用K-means算法对孔群聚类分析，以距离作为相似性的评价指标，从而孔群被划分为两类，得到两个更加合理、紧凑的孔群区域。

(2)模拟退火算法在初始种群选择方面，为了避免产生较差的个体，提高收敛的效率，采用贪婪选择策略选取较优的个体；变异是产生新个体，增加种群多样性的关键。因此在模拟退火算法中加入DIM变异算子，避免算法陷入局部最优解。

(3)仿真实验可知，本文设计的方案比改进模拟退火算法求得最优路径缩短了17.39%，使得HDI板孔群加工路径的距离有了较大提高，同时优化结果在迭代30次左右趋于稳定，运行效率得到提高。